河南省铁路-航道货运多层复合网络鲁棒性研究

李杲岭，韩明琪，狄 帅

(郑州综合交通运输研究院有限公司，河南 郑州 450000)

0 引言

发展多式联运，是加快优化运输结构、促进物流业降本增效、实现“碳达峰”“碳中和”愿景的重要手段之一。2021年，在《推进多式联运发展优化调整运输结构工作方案(2021—2025 年)》中提出“推动各种交通运输方式深度融合”“推动大宗物资‘公转铁、公转水’”。河南省紧跟国家推进多式联运发展工作步伐，发展铁水联运成为运输结构调整的主基调之一。

河南省作为我国交通运输大省，铁路方面，构建起以米字形高速铁路网和“四纵五横”普速铁路网为骨架的铁路网；水运方面，淮河、沙颍河等主要航道流经河南。2018—2022年河南省铁路和水运里程如表1所示，截至2022年底，河南省铁路运营里程6 331.7 km，水运通航里程1 825 km，较2018年复合增长率分别为3.77%和3.52%。2018—2022 年河南省铁路和水运货物运输量如表2 所示，其中2022 年河南省铁路和水运货运量分别为1.09 亿t 和1.78 亿t，分别占全社会货运量的4.21%和6.88%，相较公路货运(占比88.91%)仍有巨大差距。与此同时，近年来由于疫情影响，以及郑州“7·20”自然灾害等对运输网络造成的干扰，很大程度上影响了居民出行和生产物流活动，使得交通运输网络的脆弱性及鲁棒性成为研究重点之一。因此，研究铁路和水运的网络特征及其抗风险能力，对于保障维护铁路和水运系统稳定性和可靠性，以及促进河南省运输结构的优化调整具有重要意义。

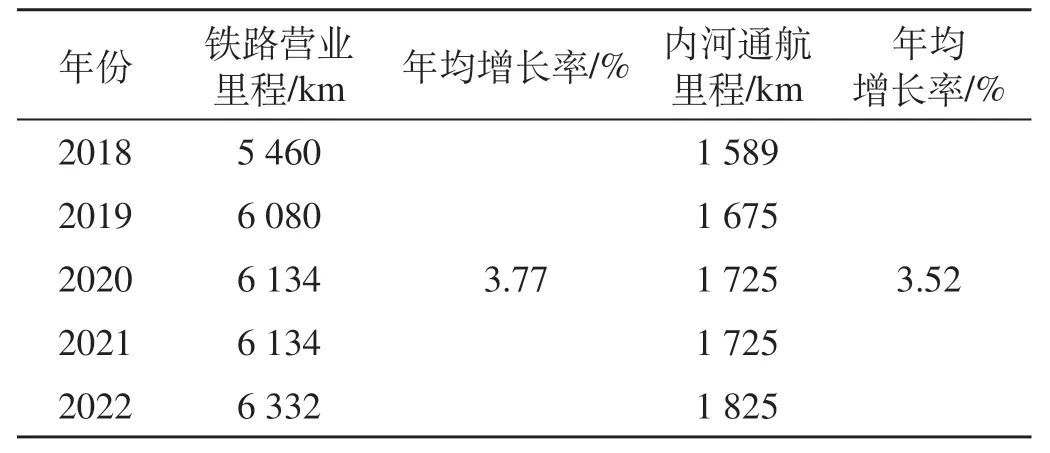
表1 2018—2022年河南省铁路和水运里程Tab.1 Length of railway and waterway in He’nan Province from 2018 to 2022

表2 2018—2022年河南省铁路和水运货运量Tab.2 Freight volume of railway and waterway in He’nan Province from 2018 to 2022

长期以来，复杂网络及其应用研究不断深入，逐渐形成了较完善的复杂网络理论体系。复杂网络建模方面，Erdos[1]，Watts[2]，Barabasi[3]等通过对现实网络进行统计学、社会学等方面的分析研究，依次提出了ER 随机网络、WS 小世界网络、BA 无标度网络等复杂网络典型模型。Newman 等[4]对复杂网络理论的发展情况进行概述，总结回顾了复杂网络领域的小世界效应、度数分布等理论概念。Cardillo等[5]首先研究了单层网络在现实领域的局限性，通过数据分析指出多层网络建模的必要性。Boccaletti等[6]从中心节点、聚类系数、矩阵和光谱特性等角度描述了多层复杂网络的结构特性。张欣[7]从多层复杂网络的定义、理论建模方法和实际应用领域3 个方面对相关代表性的研究理论进行了梳理总结，并将多层复杂网络划分为多维型和依存型2种形式。复杂网络鲁棒性方面，Albert等[8]率先提出了网络鲁棒性的概念。接婧[9]对鲁棒性的研究现状进行了梳理，内容涉及鲁棒性的定义、特点等，并概况了鲁棒性在现实中的应用。交通运输网络拓扑分析和鲁棒性研究方面，刘庆法等[10]构建了区域高速公路网络，并从点度与度分布、平均路径长度等指标对网络的拓扑结构进行定量分析，同时模拟分析了在随机和蓄意攻击下高速公路网络的抗毁性与鲁棒性。徐凤等[11]综合运用复杂网络中心度理论、统计分析和系统聚类等方法，对我国主要样本城市构成的空铁复合网络进行了枢纽集散点测度。赖丽萍[12]对轨道交通网络进行系统性分析，提出了将连通度、网络效率等作为鲁棒性的评估指标。陆秋琴等[13]运用原始法和对偶法构建了煤炭运输公路网络模型，并对其可靠性进行仿真分析。文略等[14]以我国西北地区普速铁路和高速铁路为研究对象，分析了铁路网络的度分布、中介中心性以及在模拟攻击下的可靠性。张光远等[15]选取成渝地区城际铁路网络进行建模和网络特性分析，并模拟随机和蓄意攻击，对网络的脆弱性和鲁棒性进行分析。

综上所述，复杂网络理论研究与应用不断深化和拓展。依照实际各节点的物理拓扑连接方式建立河南省铁路-航道网络复合网络模型，剖析运输网络的拓扑特性及网络可靠性，一方面将多层复合网络理论与鲁棒性分析相结合，能够为多层网络物理拓扑模型理论提供交通运输系统的现实验证；另一方面，有利于结合疫情和洪灾形势，点明加强河南交通基础设施节点和线路建设的重要性，从网络分析的角度指出当前运输网络建设和运营的较突出问题；同时，基于运输网络在不同攻击方式下的鲁棒性表现，提出网络优化的具体建议，对相关部门决策和方案制定具有重要参考意义。

1 铁路-航道多层复合网络建模

1.1 多层复杂网络模型

如何利用合理的多层网络模型描述客观系统的拓扑状态一直是学者们研究的重点，Boccaletti等[6]提出将多层网络看作是多个单层网络的集合，不同单层网络间通过层内节点与其他层网络节点的连接共同组成多层复杂网络。运用这种模型，可以较为直观地表述一个交通运输网络中，不同运输方式系统的组合与衔接关系。采用W表示多层网络集合，公式如下。

式中：G为所有单层网络的集合；C为所有不同单层网络间连边的集合，公式如下。

式中：M为网络层数。

Gα表示某α层网络集合，公式如下。

式中：Vα为α层网络的节点集合；Eα为α层网络内节点间的连边集合，公式如下。

式中：为α层网络中第1个节点；m为α层网络节点的总数；为α层网络内节点与节点间的连边。

同时，用C[α，β]表示α层与β层间的连边集合，公式如下。

式中：Vα为α层网络的节点集合；Vβ为β层网络的节点集合；E[α，β]为α层和β层的层间连边集合。

1.2 子网络与复合网络的构建

综合考虑铁水复合运输网络的现实特性，针对网络构建，主要包含以下基本假设及说明。

（1）单层网络节点：铁路网络中节点为具有货运性质的站点；航道网中节点为具有货运性质的港口和码头。

（2）单层网络的边：在铁路网络中，若两节点间可通过铁路线直达且线路中不含其他节点，则视为这两个节点间存在一条连边；航道运输网络的连边性质同理，不再赘述。

（3）网络复合(网络间的连接)：当铁路网和航道网节点和连边确定的情况下，若某铁路节点与某航道节点在地理位置上距离较近，且二者间存在依托公路完成货运直达的条件，则视为该两个节点间存在层间连边。

（4）无向网络：铁路、航道运输子网络和复合网络均为无向网络，暂不考虑网络内节点间的货流方向。

（5）无权网络：各网络均为无权网络，即不考虑不同连边上运输量的差异，边权均为1。

（6）影响距离设定：考虑实际的灾害情况，当网络中某节点遭受攻击时，在其地理位置上一定距离范围内的周围节点同样会受到攻击。初步设定两节点空间距离≤5 km 时，在攻击仿真过程中视为同一节点存在。

根据河南省铁路和航道基础设施建设现状，并结合河南铁路货运站和港口码头货运流量数据，经过筛选得到铁路运输节点如表3 所示，航道运输节点如表4所示。

表3 铁路运输节点Tab.3 Railway transport nodes

表4 航道运输节点Tab.4 Waterway transport nodes

将铁路网和航道网中的节点分别依照运输路径进行连边，并以邻接矩阵的形式导入Gephi 软件，得到铁路-航道子网络与复合网络拓扑结构如图1所示。其中，铁路运输网络如图1a所示，由160个节点和182 条连边组成；航道运输网络如图1b 所示，由55 个节点和59 条连边组成；将铁路节点和航道节点进行连接，得到铁路-航道复合网络如图1c所示，由215个节点和295条连边组成。

图1 铁路-航道子网络与复合网络拓扑结构Fig.1 Topology structure of rail-water individual network and composite network

2 拓扑特征分析

2.1 常用拓扑指标

通过上述网络构建过程，将运输网络简化为由站点和线路构成的静态网络。针对复杂网络系统的静态结构特性，复杂网络基本统计指标如表5所示。

表5 复杂网络基本统计指标Tab.5 Basic statistical indicators of complex network

2.2 拓扑性质分析

依据上述复杂网络基本统计指标的描述，借助复杂网络分析软件计算得到网络拓扑特征值如表6所示，3 种网络度分布的幂拟合曲线如图2 所示，3种网络度分布的对数拟合曲线如图3所示，3种网络度分布拟合程度如表7所示。

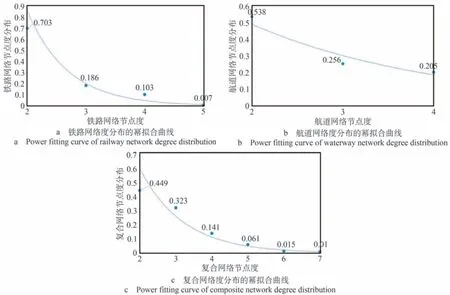
图2 网络度分布的幂拟合曲线Fig.2 Power fitting curves of networks degree distribution

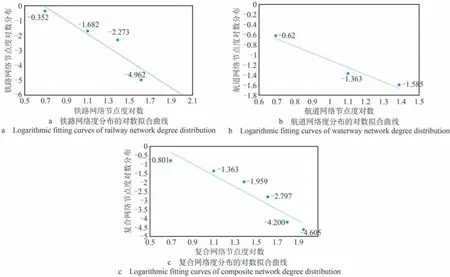
图3 3种网络度分布的对数拟合曲线Fig.3 Logarithmic fitting curves of three networks degree distribution

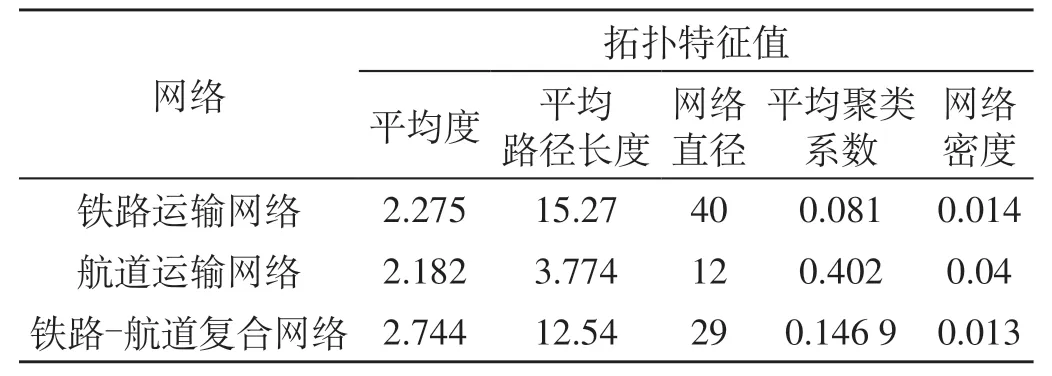
表6 网络拓扑特征值Tab.6 Topology characteristic value of networks

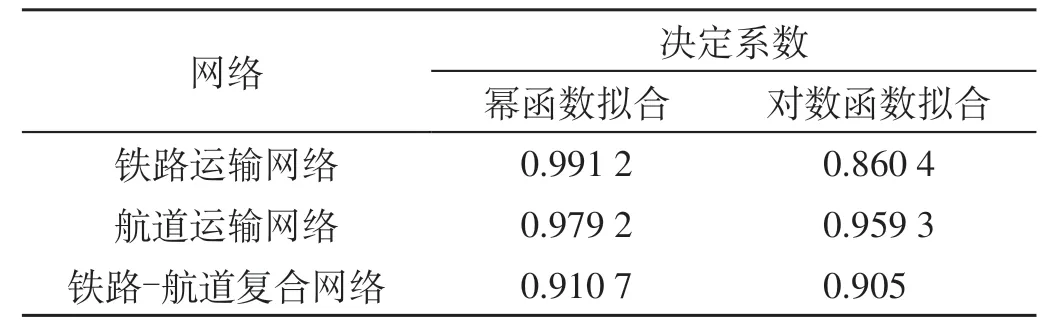
表7 3种网络度分布拟合程度Tab.7 Fitting degree of network degree distribution

首先，从各个网络的拓扑特性上分析。航道网络相较同等规模的随机网络具有较小的平均路径长度以及较大的聚类系数，由此得出航道网络具有显著的小世界特性；铁路网络和复合网络的平均路径长度值很大，聚类系数较小，故判断二者不具备显著的小世界特性。由上述图表可知，铁路网和航道网的节点度分布服从幂律分布，二者具有显著的无标度特性，而复合网络的拟合程度较差，故判断其不具有显著的无标度特性。

其次，根据各网络拓扑指标值结合现实分析。从网络连通性上考虑，子网络与复合网络的节点平均度值均在2~3 之间，度值为2 的概率最大，结合地理位置因素可以分析得到当前河南省铁路和航道货运主要分布在较为关键的高等级航道和铁路干线上。从社团特征上考虑，航道网的平均聚类系数较铁路网和复合网络更大，且网络密度和模块度值也更大。由此说明航道网络的群落结构特征较明显，不同航道间形成小集体，而铁路基础建设受地理因素的影响较小，铁路网和复合网络在整体上的群落特征不明显，网络节点分布相对较均匀。

3 鲁棒性仿真评价

3.1 评价内涵

鲁棒性是指一个复杂系统内部部分条件发生变化时维持其自身稳定的能力，也叫容错能力。交通运输作为地区经济的命脉，承担着货物输送和人员流动的作用，如今的交通网络不断呈现复杂性、关联性等特征，鲁棒性是运输网络在特定状态下能否正常运作的关键。当地区交通运输网络的部分节点或线路遭受破坏时，势必会引起一系列的连锁反应，若因此无法在约定期限内完成既定的客、货运输，就会造成一定经济损失和社会后果。鲁棒性分析在交通运输网络中的意义，在于评价运输网络局部遭受破坏时自身的稳定性，并由鲁棒性结果给出针对性的措施以提升其鲁棒性。

随机攻击指在网络中随机攻击部分节点或连边，在现实交通系统中往往代表着由于地震、洪水等不可控因素造成的站点无法正常运作或交通线路瘫痪等；蓄意攻击即根据网络中节点或连边的拓扑特征，模拟有目的性的恐怖袭击等条件下，按照节点的重要程度(如节点度、介数等)对网络节点与边依序攻击，由此造成网络的规律性破坏。网络鲁棒性评价仿真流程设计如图4所示。

图4 网络鲁棒性评价仿真流程设计Fig.4 Design of simulation process for network robustness evaluation

3.2 评价指标

为分析研究运输网络的有效性和连通性，分别选取网络效率和最大连通子图相对大小作为河南省铁路、航道子网络和复合网络鲁棒性仿真的评价指标。

（1）网络效率。

εij表示任意节点对之间路径效率，公式如下。

式中：Lij为网络节点i，j之间的最短路径。

复杂网络全局效率E表示网络中任意节点对之间路径效率的平均值，公式如下。

式中：n为网络中的节点总数。

（2）最大连通子图相对大小。

假设复杂网络对应的拓扑图G中存在一些子图，若每个子图中所有节点之间都有路径相连，但在不同子图间不存在节点连通，则称这些子图为连通子图，其中包含有最多节点集合的连通子图称为最大连通子图。复杂网络的最大连通子图相对大小用S表示，公式如下。

式中：n′为网络中最大连通子图所含的节点数。

3.3 结果分析

采取随机数生成的方式标记节点从而进行随机攻击，采取按节点度值排序的方式进行蓄意攻击。利用数据分析软件对3 种网络分别进行攻击仿真，得到航道网络鲁棒性指标变化如图5 所示，铁路网络鲁棒性指标变化如图6 所示，航道-铁路复合网络鲁棒性指标变化如图7所示。

图5 航道网络鲁棒性指标变化Fig.5 Changes in robustness indicators of waterway network

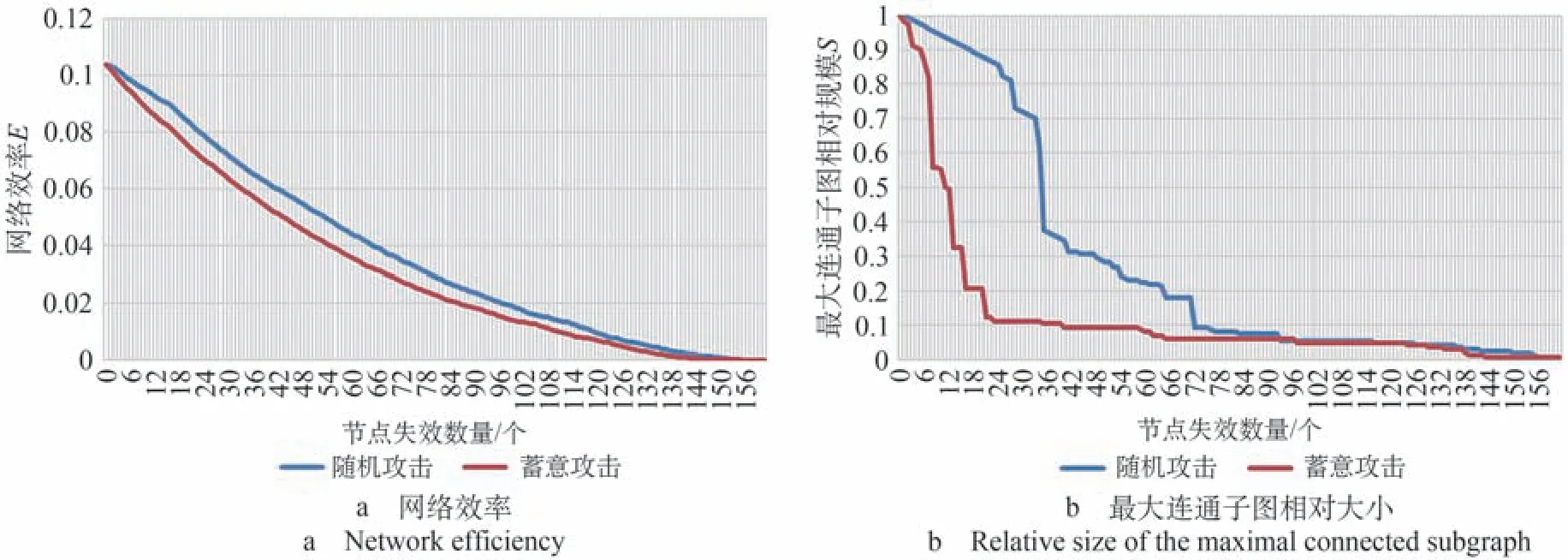
图6 铁路网络鲁棒性指标变化Fig.6 Changes in robustness indicators of railway network

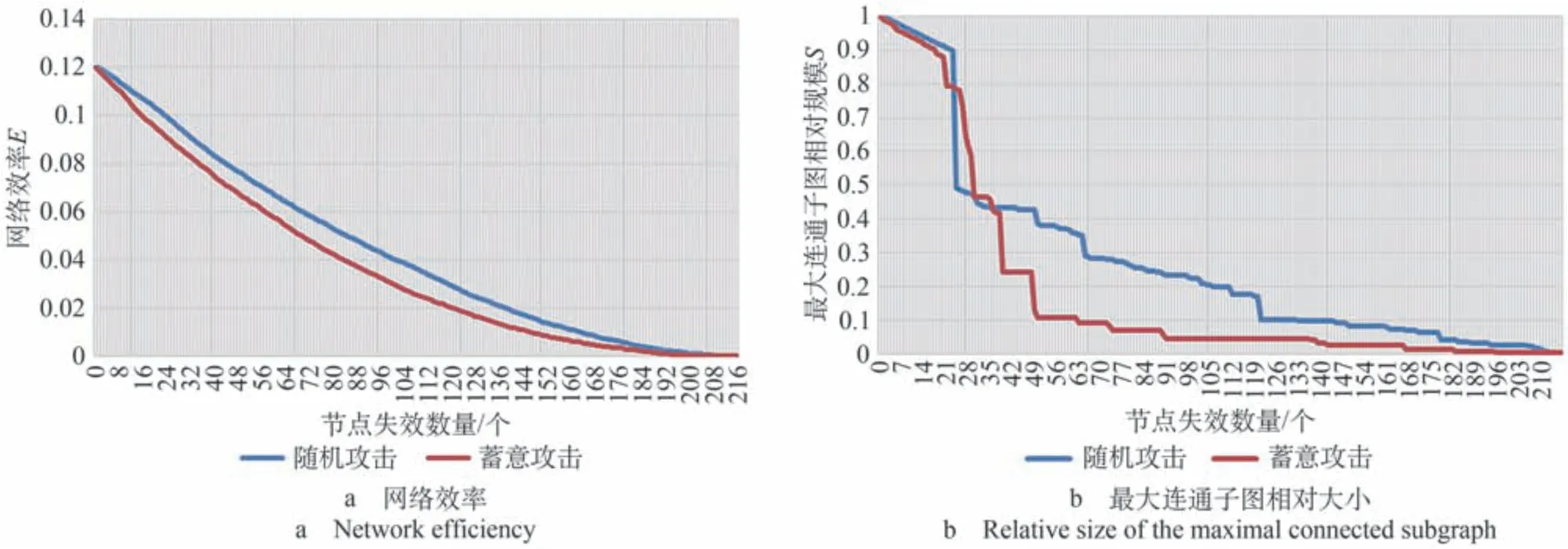
图7 铁路-航道复合网络鲁棒性指标变化Fig.7 Changes in robustness indicators of rail-water composite network

从图5 可以看出，两类指标在随机攻击下的下降趋势较为平缓，而蓄意攻击下的变化曲线则出现多个明显断层，意味着蓄意攻击对航道网的破坏性更强，网络在部分关键节点受攻击的情况下其相应指标会大幅度下降。当分别随机删除航道网中的54 个节点或按节点度排序删除53 个节点时，网络效率下降至0；同样地，航道网在随机攻击、蓄意攻击下节点失效数目分别达到54，41 时，网络中再无连通子图存在，此时所有节点间的连通性将会彻底消失，即网络完全瘫痪。结合实际航道网的港口(码头)分布与线路走向，由于大多数港口码头处于单独的内河航道上，在蓄意攻击下将这些相互独立的航道上节点度较高且不超过半数的港口码头破坏后，网络中的所有点到点运输将无法进行。

从图6 可以看出，铁路网络的指标变化曲线同样在蓄意攻击下呈现出下降更快的趋势。铁路网由于初始聚类系数较低，在受到随机攻击和蓄意攻击时曲线走势有一定程度的接近；而在两种攻击方式下，其最大连通子图相对大小曲线则相距甚远。铁路网在随机攻击、蓄意攻击下节点失效数目分别达到160，158时，网络效率下降至0；而当随机或蓄意删除网络中的156，143 个节点时，网络中再不存在连通子图，网络完全瘫痪。值得注意的是，由图6b 显示的最大连通子图曲线表明，当对铁路网进行随机攻击时，初期曲线下降较为平缓，而在失效中期则出现大幅下降的断层点；而对应蓄意攻击下，在节点失效初期网络的最大连通子图相对规模即呈现出大幅下降。结合现实分析，在铁路网部分关键节点遭受破坏的情况下，网络初始的网格化布局将发生巨大改变，这些关键节点即为不同网格的连接点，其具有较大的节点度值，这与实际铁路网的多“纵横”构建布局息息相关。

从图7 可以看出，对于航道网和铁路网相结合的复合网络，其由聚类系数和最大连通子图相对大小表现出的鲁棒性较航道、铁路子网络更强。复合网络在随机攻击和蓄意攻击下节点失效数目分别达到215，214时，网络效率下降至0，有效性完全丧失；而当随机攻击和蓄意攻击下失效节点数目分别达到213，196 时，复合网络中再无连通子图存在，所有的节点均孤立存在。将复合网络的鲁棒性结果与铁路、航道子网络进行横向对比，可以发现失效节点数目相同时复合网络的指标值更大；同样地，复合网络完全瘫痪时对应的攻击效率更高，鲁棒性综合表现更好。依据以上对比分析，可以发现复合网络的指标曲线与铁路网络的曲线相似度较高，初步得出由于铁路网节点数与连边更多，在复合网络中作为主导部分，由此得出河南省的大部分货物运输对铁路的依赖性更强。航道网的优势则在于，其受到攻击后指标曲线下降的趋势较为缓和，对关键点的依赖性较小。

4 措施及建议

（1）打通各条航道隔离，加强内河水运衔接。由于河南省内主要水运航道间连通性不足，当某水运航道遭受破坏后，该线路上原有的货物难以由其他水运线路承接运输，易出现货物留滞现象。结合河南省相关部门对航道、港口的近远期规划，为加强河南省内河航道抗风险能力，建议应重点提升沙颍河、洪汝河等航道等级和通航能力，考虑打通贾鲁河与周边航道的衔接，进而增强河南省内河水运集疏运能力。

（2）增强铁路干线抗毁能力，提升铁路网综合承载能力。河南省铁路整体运量巨大，由拓扑图可知货运站数量虽多但却主要分布在铁路干线上，货物在铁路网内的周转对干线的依赖性大，主要干线铁路货运承载率较大，难以满足未来铁路货运量的持续增长；且一旦干线节点、线路遭受破坏，铁路支线承载力不足，极易出现货物留滞。为保障河南省铁路货运的可持续发展，建议重点加强京广铁路(北京丰台—广州)、陇海铁路(兰州—连云)等干线基础建设和运营组织，同时应适当考虑在郑州、平顶山等地周边增建货运支线。

（3）加强多式联运通道建设，打造多方式运输衔接模式。通过鲁棒性研究，表明铁水联运较单一运输方式具有更强的抗风险能力。因此，如何进一步促进不同方式的衔接与融合也是未来的重点。考虑在货源分布密集地区的不同方式节点间建设多式联运的专用线路，大幅提升区域运输的组织协调能力。例如，通过加快周口港中心港区、信阳港淮滨港区等铁路专用线建设，提升内河港口码头与铁路干线的货运衔接能力。

（4）加强关键节点的日常运营和维护。鲁棒性研究结果表明，蓄意攻击下各网络在节点破坏初期，其性能评价指标即出现较快的下降速率。为防止关键节点毁坏对河南省区域货运能力造成的严重影响，应重点加强圃田站、周口港中心港区等关键节点的日常维护和监查，建立风险防控机制，保障突发情况下的稳定运营。

5 结束语

在构建河南省铁路、航道节点网络和复合网络的基础上，对子网络和复合网络进行拓扑分析，得到航道网络具有小世界特性，而铁路网络和航道网络具有无标度特性的结论；通过对各网络进行鲁棒性分析和比较，一方面识别出网络内的关键节点，另一方面得出复合网络鲁棒性更强的结论，对于指导水运和铁路网络的运行维护，加强不同联运方式衔接具有重要意义。此外，由于构建的网络是无向无权网络，未考虑货物权重在网络中的变化，下一步应在运输网络构建和分析过程中考虑节点和线路在货运负载限制下的拓扑特性和鲁棒性变化，同时可引入货运价格、时间成本等多种因素，更加准确地模拟和分析运输网络的拓扑状态和抗毁性。