基于客流博弈均衡的旅客列车双层开行方案优化
汤振源
(中铁二院昆明勘察设计研究院有限责任公司 工程设计一处,云南 昆明 650200)
0 引言
旅客列车开行方案以客运量为基础,是运输组织的重要内容之一。旅客列车开行方案优化问题一直是该领域学者重点研究的课题。
列车开行方案方面,周文梁等[1]、付慧伶等[2]、秦进等[3]构建了考虑旅客出行需求的列车开行方案优化模型,并采用智能算法对其进行求解;史峰等[4]构建旅客列车开行方案双层规划模型,并设计GP 算法求解下层多类用户均衡模型、模拟退火算法求解上层旅客列车停站方案模型的混合算法,该研究运用成熟的交通流均衡理论解决了下层铁路旅客均衡问题;黄林尧等[5]、王正彬等[6]通过考虑旅客出行时间等因素,构建了旅客列车开行方案优化模型,并设计遗传算法作为模型求解算法;Qi等[7]提出双目标混合整数线性规划模型,并运用GAMS对该模型进行求解;Dong 等[8]基于旅客时间依赖性,构建了列车停站方案与列车时刻表集成的组合优化模型,并设计混合整数非线性规划算法得到该模型优化解;Cacchiani 等[9]通过考虑旅客数量的不确定性,构建了混合整数线性规划模型来获得列车鲁棒性停站方案。
客流均衡分配方面,王莹等[10]通过确定不同弧段出行费用及能力约束,构建了整数网络化客流分配模型;Meng 等[11]通过分析各类铁路旅客的动态选择行为,构建了需求-服务-资源组合优化模型,并设计了拉格朗日松弛算法;Niu 等[12]考虑铁路旅客时变性,构建二次整数规划模型,并设计精确非线性混合整数算法;孙晟凯等[13]通过分析地铁高峰时段客流时空分布特征,提出了列车与客流动态交互评价模型;Jiang 等[14]通过分析拥挤条件下地铁旅客进站流控制与列车实时调度关系,构建了以旅客滞留惩罚值最小为目标的组合优化模型,并设计基于Q-Learning的算法求解该模型。
综上,既有研究主要借鉴传统交通客流分配理论研究铁路旅客出行问题,对铁路旅客多样性选择及潜在出行博弈分析较少,从铁路与旅客2 方考虑,通过引入非合作博弈,提出一种旅客出行选择均衡方法,并以此为下层模型构建纯整数非线性多目标双层规划模型,以获得铁路与旅客均满意的高速铁路开行方案。
1 模型构建
1.1 基本假设
该模型做如下假设:①依据单线高速铁路制定开行方案,即仅考虑本线列车及本线客流;②上下行客流均衡;③不考虑递远递减对铁路票价的影响;④对旅客换乘时间不加考虑。
1.2 基本符号
记ts为列车在站平均停留时间,铁路旅客根据消费水平分为g个层次,则不同OD 间客流f(i,j)按照消费层次可以划分为f w(i,j),其中w=1,2,…,g。将w消费层次客流中乘坐列车T的客流表示为(i,j),则(i,j)中的客流个体可记为(i,j)。基本符号说明如表1所示。

表1 基本符号说明Tab.1 Description of basic symbols
1.3 上层停站方案模型
记上层0-1 决策变量为x(T,si),其值为1 表示列车T在si停车。列车公里费用函数CT为
列车固定使用费用函数Cfix为
客票收入函数Cticket为
则铁路净收益目标函数f1为
列车空座位走行距离目标函数f2为
上层开行方案模型应满足如下2 个基本约束条件。
(1)列车停站约束,如公式⑹所示。
式中:β表示停站率。
(2)通过能力约束,如公式⑺所示。
1.4 下层客流博弈均衡模型
记w消费层次客流的时间价值为σw,则OD 为i,j的w消费层次客流个体per选择乘坐列车T的票价费用函数(i,j)与时间价值函数(i,j)分别如公式⑻、公式⑼所示。
式中:M为惩罚因子。
总加权费用函数(i,j)如公式⑽所示。
式中:为权重值,表示w消费层次客流对票价、时间的敏感度,满足
w消费层次客流个体per乘坐列车T的效用函数(i,j)如公式⑾所示。
w消费层次客流的人均效用函数(i,j)如公式⑿所示。
则客流个体per的满意度评价函数(i,j)如公式⒀所示。
下层非合作博弈[15-17]客流均衡模型中博弈要素说明如下。
(1)局中人:同一OD 相同消费层次客流个体per。
(2)纯策略:规定局中人per的策略为所选择乘坐的列车T,以∈N表示。
(3)纯策略集:以θijwper={|∀l∈L,T∈ω(l),x(T,si)= 1,x(T,sj)= 1}表示局中人per的可选策略集合。
(6)纯策略局势:以∈×θijwper表示OD 为i,j的w消费层次中所有客流个体per的可选策略所构成的f w(i,j)维向量。
由于纯策略为混合策略的特例,故混合策略意义下的期望赢得函数如公式⒁所示。
由公式⑻至公式⒁知下层客流博弈均衡满意度评价目标函数如公式⒂所示。
由纳什均衡定义可知,公式⒂对应的最优解应为0。
下层客流博弈均衡分配模型应满足如下3 个基本约束条件。
(1)客流博弈均衡条件如公式⒃所示。
(2)列车上座率约束如公式⒄所示,该约束为联系上下层联系反应函数。
(3)以同一OD间相同消费层次客流中选择乘坐列车T的客流个体为决策变量,如公式⒅所示。
2 算法设计
运用数学理论求解双层规划[18]精确最优解有很大困难,所构建的纯整数双层非线性规划模型属于典型的NP-Hard问题,运用最优化理论很难在多项式时间内找到问题的解。因此,具有随机、并行和分布式特点且对问题无连续性要求的群智能算法在求解双层规划问题时凸显其优势,针对构建的模型特征,采用NSGA-Ⅱ算法求解上层停站方案模型,QPSO算法求解下层客流博弈均衡模型[19]。
规定任意开行区段内的列车种类数按停站方式确定为一站直达(以整数“1”表示)、大站停(以整数“2”表示)、择站停(以整数“3”表示)和站站停(以整数“4”表示)4种。
步骤1:确定开行区段。开行区段编号示意图如图1所示。

图1 开行区段编号示意图Fig.1 Operation section coding
步骤2:调整原始OD客流表。跨区段OD客流调整如图2所示。

图2 跨区段OD客流调整Fig.2 OD passenger flow adjustment in cross-regional section
步骤3:确定上层染色体编码形式。染色体编码方式如图3所示。
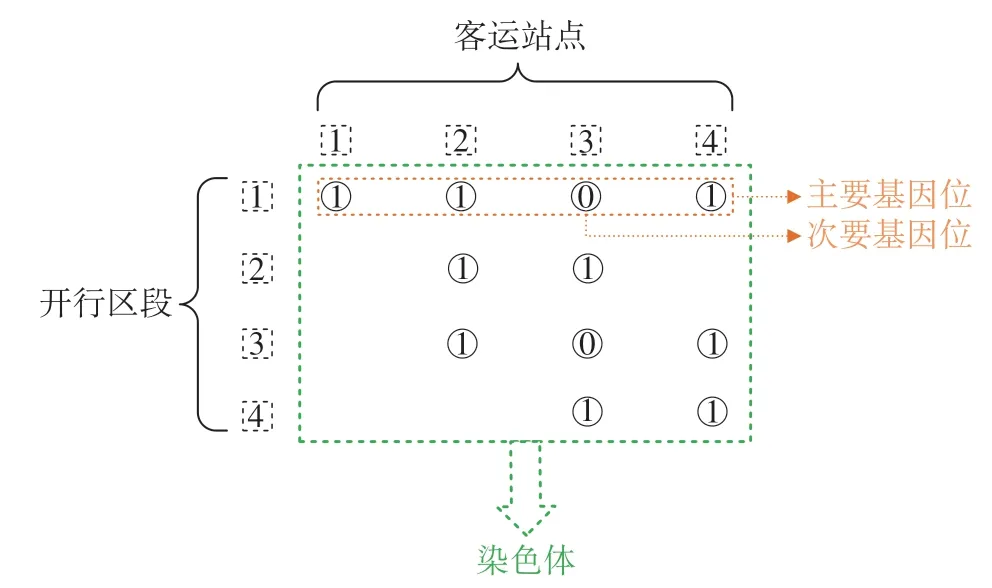
图3 染色体编码方式Fig.3 Chromosome coding mode
步骤4:消除约束。运用外罚函数法消除约束
公式⑹、公式⑺、公式⒄,则公式⑷、公式⑸、公式⑽如公式⒆至公式所示。
式中:υ≥0 为惩罚因子;G1,G2,G3和G4分别为公式⑹、公式⑺、公式⒄所对应的罚函数项。
步骤5:初始化上层种群X。
步骤6:求解下层纳什均衡解。针对每个上层解x,初始化下层种群Y,种群Y按照公式、公式所进化方程迭代更新。
式中:t表示下层迭代次数;pijwper(t+ 1)表示局部吸引子;随机变量uijwper(t)~U(0,1);ϑ为收缩-扩张系数;lijwper(t+ 1) 为特征长度;mijw(t) 为平均最好位置。
步骤7:上层算法迭代。单点交叉操作示意图如图4所示,简单变异操作示意图如图5所示。

图4 单点交叉操作示意图Fig.4 Single-point crossover operation

图5 简单变异操作示意图Fig.5 Simple mutation operation
将步骤6 中求得的下层纳什均衡解yNash回代至公式⒆、公式⒇,对上层种群X执行非支配排序、拥挤度算子,然后执行图4、图5所示的进化算子。
步骤8:判断迭代次数是否满足,若满足,算法终止,方案输出。
3 案例分析
3.1 案例背景
以兰新高速铁路(兰州西—乌鲁木齐)为例,兰新高速铁路站点示意图如图6 所示。兰新高速铁路列车开行区段及其编号示意图如图7 所示。兰新高速铁路站点编号如表2 所示,开行区段站点如表3所示。
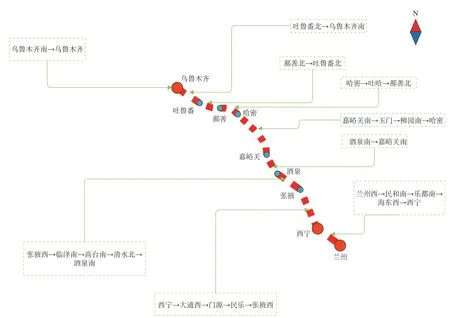
图6 兰新高速铁路站点示意图Fig.6 Lanzhou-Xinjiang High Speed Railway Station
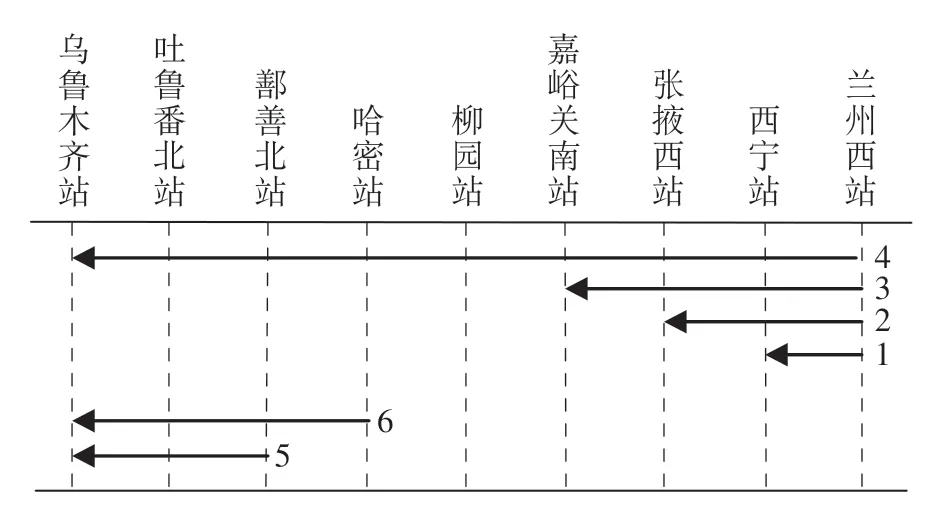
图7 兰新高速铁路列车开行区段及其编号示意图Fig.7 Train operation sections and their numbers in Lanzhou-Xinjiang High Speed Railway

表2 兰新高速铁路站点编号Tab.2 Station number of Lanzhou-Xinjiang High Speed Railway

表3 兰新高速铁路区段划分Tab.3 Division of Lanzhou-Xinjiang High Speed Railway sections
3.2 案例求解及结果分析
记列车座位等级μ={1,2,3};列车种类u={1,2,3,4};编组辆数b= 8,为固定编组;票价率r={{0.9,0.8,0.7,0.6},{0.6,0.5,0.4,0.3},{0.4,0.3,0.1,0.1}};列车公里费用c= 500元;列车固定费用cfix= 1 000元;列车旅行速度v= 250 km/h;车辆定员A= 800 人;列车在站平均停留时间ts=4 min;列车最低载客率= 0.6;列车最高载客率= 1.1;客流波动系数ϕ=1.3;列车停站率β=0.6;w=1的消费层次客流时间价值= 200元/h;w=2的消费层次客流时间价值= 100 元/h;w=3 的消费层次客流时间价值= 50 元/h;惩罚因子M=υ=5 000 000 000;权重系数= 0.1,= 0.9,= 0.5,= 0.5,= 0.9,= 0.1;收缩-扩张系数ϑ=0.5。
算法迭代次数Gen=500,上层种群数量chroms=200,交叉概率pc=0.95,变异概率pm=0.01,下层种群数量partics根据区段相同消费层次客流人数动态确定。
未按拥挤度值选取的前5 层Pareto 前沿值如图8 所示。分析图8 可知:函数f1的收敛速度较函数f2的收敛速度慢,说明上层开行方案对列车空座位走行公里的影响较收益目标函数小,反映了运用下层非合作博弈理论进行客流均衡分配可有效降低列车开行费用。
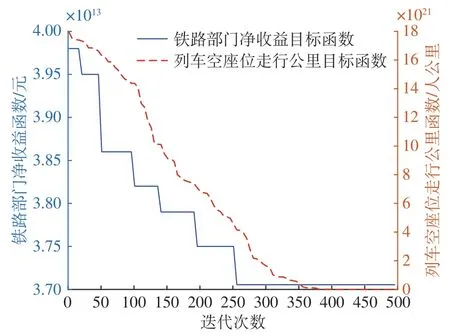
图8 未按拥挤度值选取的前5层Pareto前沿值Fig. 8 Pareto frontier values selected without considering congestion values
迭代次数达500 次时的未按拥挤度值选取的前5层Pareto值如图9。由图9可知,当f1值减小时(图中为横坐标值增大时),各层f2值(图中纵坐标值)的波动差异较小,列车空座位靡费值较为稳定。由于横坐标值增大意味着解是违背停站率约束的,故两目标函数具有冲突性,f2值的优化在一定程度上会降低f1值的精度,说明运用NSGA-Ⅱ算法解决该模型的合理性。
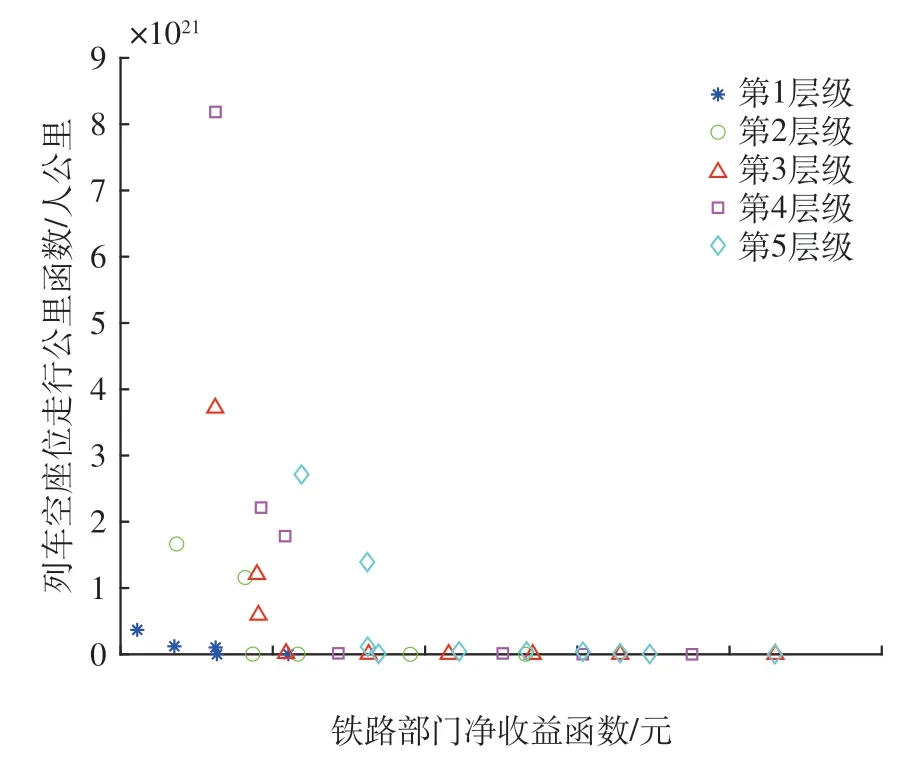
图9 未按拥挤度值选取的前5层Pareto值Fig.9 Pareto values of first five layers selected without considering congestion values
按拥挤度值选取的前5 层Pareto 值如图10 所示。由图10 可知,NSGA-Ⅱ算法中按照拥挤度值从大到小选择解个体可使Pareto前沿解的分布更加均匀;均为负相关函数,非支配序为2,3,4,5所对应的散点图(即图10中的第2,3,4,5层级散点图)负相关程度均比非支配序为1 (即图10 中的第1层级散点图)的Pareto前沿解相关度要大。结合图9 分析结果,当铁路收益值增加时,列车空座位走行公里数也增加,因此,选取铁路收益值最大化,且列车空座位靡费较少、列车空座位走行公里值最小化的非支配序为1 的Pareto 前沿解是科学合理的。
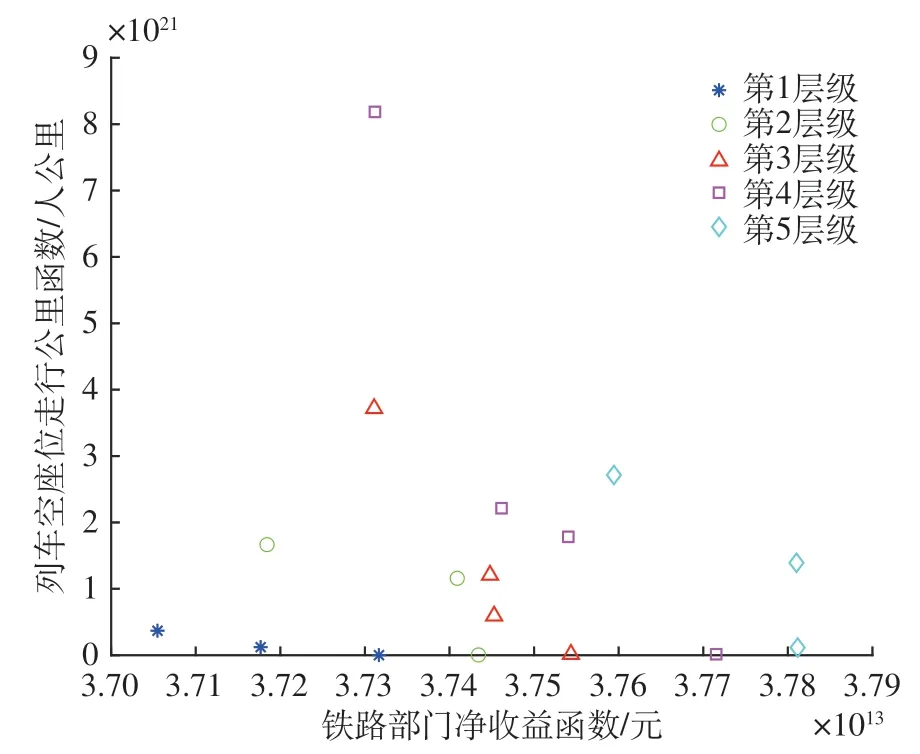
图10 按拥挤度值选取的前5层Pareto值Fig.10 Pareto values of first five layers selected according to congestion values
综上,对上层每一代产生的解集,由算法流程及程序运行结果知,下层客流分配均能很好地收敛,故选取上层非支配序为1 的层级解集为Pareto前沿解,得到以下5种开行方案。开行方案1如表4所示,开行方案2如表5所示,开行方案3如表6所示,开行方案4如表7所示,开行方案5如表8所示。
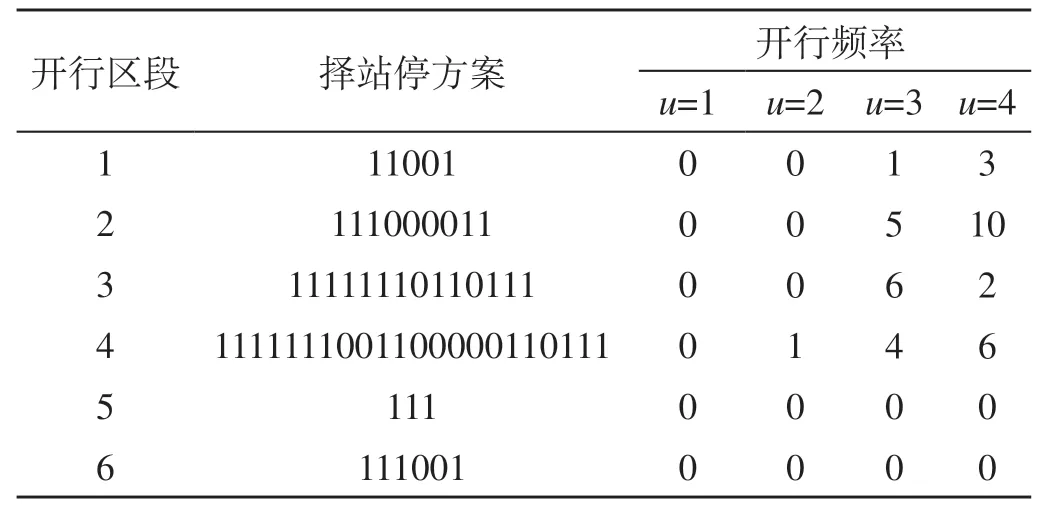
表4 开行方案1Tab.4 First train operation plan
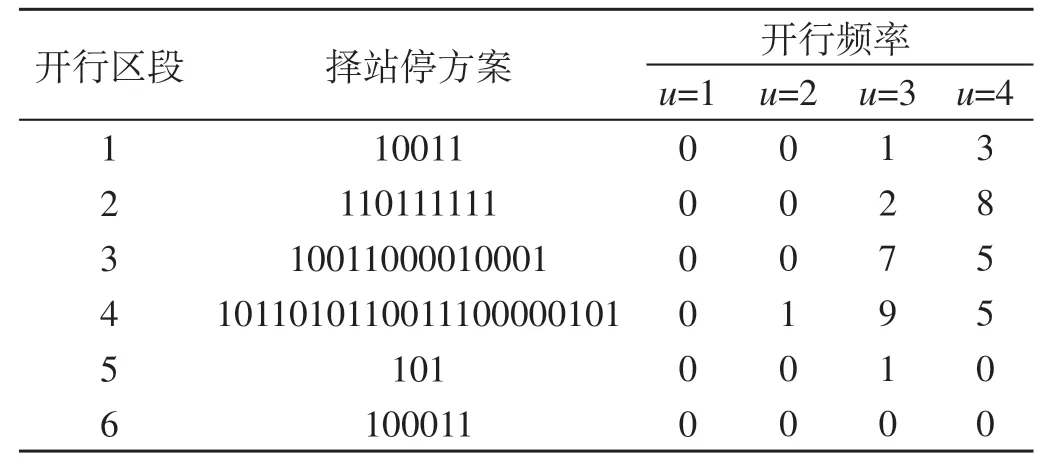
表5 开行方案2Tab.5 Second train operation plan

表6 开行方案3Tab.6 Third train operation plan
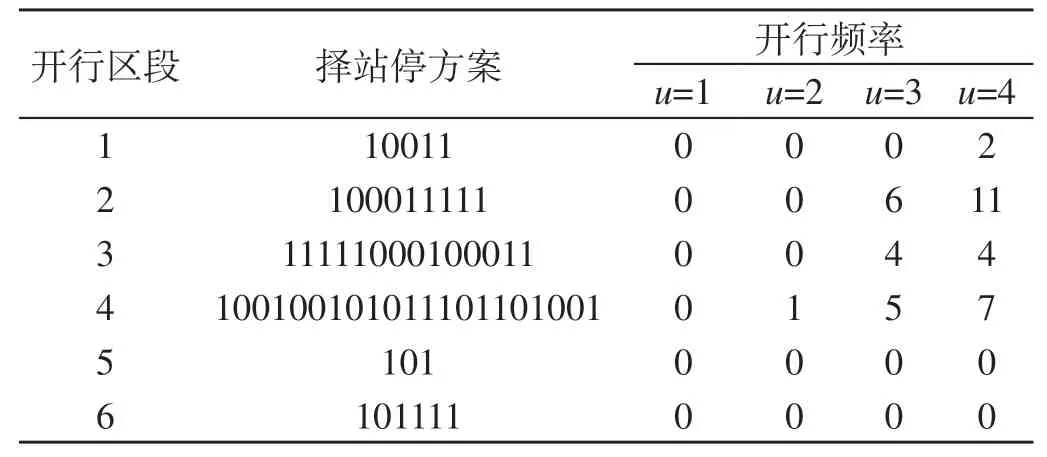
表7 开行方案4Tab.7 Fourth train operation plan

表8 开行方案5Tab.8 Fifth train operation plan
分析表4至表8可知,开行方案1—5中:
(1)开行区段1—6均未开行一站直达列车,这是因为模拟OD客流数据波动性较小造成的,使得各开行区段起讫点客流不能满足开行直达列车的要求。
(2)开行区段6 未开行任何一类列车,这是因为即使会出现换乘现象,从哈密站上车、到达吐哈站及其以远的旅客选择开行区段4 和5 乘坐列车完成出行的效益较开行区段6 高,另一方面,这反映了双层规划的上下层关系:上层决策者对下层决策者具有支配作用,但这种作用不是绝对的,下层在上层指定的容许范围内可自主决策,并反作用于上层。
(3)只有开行区段5 开行一对大站停列车,这是由于6 个开行区段中只有开行区段5 同时包含兰州西站、西宁站、乌鲁木齐站。
(4)开行区段5 择站停列车的开行,能够降低开行区段4 站站停列车的开行对数,可有效减少长远距离旅客的出行时间,因此,可将开行方案2 与开行方案5作为备选较优开行方案。
由算法迭代结果知,开行方案5 与开行方案2相比,所对应的铁路净收益目标函数值最大,并且站站停列车开行频率最小,故确定开行方案5 为最终满意开行方案。满意开行方案如图11所示。

图11 满意开行方案Fig.11 Feasible and satisfactory train operation plan
4 结束语
综合考虑铁路运营部门与铁路旅客两方利益,首先运用双层规划模型刻画两方利益博弈关系,通过求解纳什均衡点来寻求使两方利益最大化的铁路部门开行方案与旅客出行选择行为;其次将现实中旅客合理假设化为不同消费层次的完全理性人,并通过OD 博弈环境划分,使相同博弈环境中各消费层次旅客均具备“理性知识”,从而做出使自身利益最大化的出行策略选择。这种基于非合作博弈的客流均衡分配方法,在兰新高速铁路实例中得以验证,由该模型及算法得出的开行方案考虑到了每位旅客,不会造成部分铁路旅客流失。

