高速铁路网列车运行径路精细化搜索算法研究
李 靖,王 涛,李 博,刘明玮
(1.中国铁道科学研究院集团有限公司 中国铁路列车运行图技术中心,北京 100081;2.中国铁道科学研究院集团有限公司 运输及经济研究所,北京 100081;3.中国国家铁路集团有限公司运输部,北京 100844)
0 引言
随着我国铁路行业快速而稳步的发展,大量高速铁路线路、车站建成并投入使用,路网规模愈发庞大,结构也愈发复杂,截至2022 年底全国高速铁路营业里程共计4.2 万余km,是德国的6 倍、法国的9 倍、日本的12 倍,同时路网内枢纽越来越多,枢纽内车站不同方向之间径路的连通关系复杂,如石家庄至沈阳高速列车径路分析如表1 所示。石家庄至沈阳的径路在北京枢纽不连通,可知在径路搜索时考虑枢纽内部的连通性具有必要性;我国高速铁路点多、线长、面广且跨线列车多,大规模成网运营已成为不同于国外高速铁路的突出特点(例如日本多为本线运行,法国多为小规模跨线运行),在实际上增大了列车运行径路搜索的难度。

表1 石家庄至沈阳高速列车径路分析Tab.1 Analysis of high speed railway train routes from Shijiazhuang to Shenyang
客流需求等因素是列车运行组织、计划编制、应急指挥工作中的重要基础,而根据客流需求的列车径路是否具有可行性需要精细化的径路搜索来支撑,径路搜索可为运输组织工作提供技术支持,实现降本增效的目的。目前国内外学者在网络构建、路径求解等方面进行了大量研究。张兰霞[1]、贺俊源[2]对我国高速铁路网特点进行分析;胡心磊等[3]对高速铁路列车径路进行了分类与分析;张羽成等[4]研究铁路网络结构存储及路径构造;毕明凯等[5]建立场站网络拓扑图并对枢纽场站分工优化求解。路径搜索算法方面,最短路求解有Dijkstra 算法[6],K 短路求解有YEN 算法[7]、双向扫除算法[8]等;启发式算法求解有A*算法[9]、B*算法[10]等。高速路网径路搜索方面,胡必松[11]利用动态规划思想采用逆序解法求解K短路问题;王喆等[12]从遗传学角度探讨两点间K 条最优路径;习子文[13]结合Dijkstra算法和双向扫除算法求解OD间的合理径路集;柳键等[14]采用一种拼接和去冗结合的K最短路算法设计客运服务网络路径搜索;范家铭等[15]采用向量限定等优化策略实现列车径路快速搜索等。
上述研究聚焦路网构建、径路搜索等方面,主要以车站或车场为路网节点,未考虑车站的结构和进路信息,在枢纽等连通关系复杂的地区径路搜索更容易产生误差,径路搜索精细化程度有待提升。本研究针对大规模复杂的高速铁路网,重点考虑详细的车站站场结构,并构建区间属性信息,提出全国高速铁路网的多径路精细化搜索算法。
1 精细化高速铁路拓扑网构建方法
高速铁路网指有动车组列车开行的高速铁路、城际铁路、高普混行线路。高速铁路拓扑网根据构建精细程度的不同,可分为宏观、中观、微观3 个层级,其复杂程度有较大差距,不同精度层级下铁路网构建涉及数据如图1 所示。宏观和中观层面下通过车站节点的线路默认连通,车站节点内线路连通关系精度不足;微观路网层面下可真实反映路网站间、站内实际连通拓扑结构。

图1 不同精度层级下铁路网构建涉及数据Fig.1 Railway network construction at different precision levels
为支持列车走行径路的全过程、精细化研究,研究建立基于车站进出口的多维度路径信息表示方法,包括车站内进路关系及区间连通关系:在车站物理网络拓扑的基础上,构建车站进路数据,并以车站进路数据为基础构建车站内进站信号节点(车站进出口)间的连通关系,以线路区间数据为基础构建不同车站间进出口的连通关系,最后实现路网层的连通拓扑构建。上述路径信息对基础路网数据的准确性和规范性有很高要求,下面从车站、线路区间实际物理拓扑结构出发,研究高速铁路网拓扑构建和径路数据表达。
1.1 车站层级连通拓扑构建
1.1.1 车站物理网络拓扑构建方法
车站的物理网络拓扑是车站进路的数据支撑,构建车站拓扑时应以车场为一个独立的车站单元,使得进路只涉及相应车场。高速铁路车站站场结构主要由道岔、信号机、轨道区段等设备构成,车站站型示意图如图2 所示,各类设备关键位置坐标由图元控制点确定(图中红点),可通过对比关键位置坐标确定各设备的左侧和右侧相邻的设备类型及名称[16]。

图2 车站站型示意图Fig.2 Railway station yard structure
通过对设备进行关联,便可构造车站物理网络拓扑,铁路车站物理网络拓扑图如图3 所示。各设备存储有本设备特征数据及相邻设备连接关系数据,研究将道岔图元拆分为3 个子节点与2 条连接边,另外将轨道区段、信号机图元拆分为2 个子节点和1 条连接边,设备间的连接关系由不同图元的子节点连接的边表示,构建车站拓扑无向图并根据图元子节点生成邻接矩阵。图3 中车站进出口(ENT)设置于站内最外侧的进站信号机,与路网区间拓扑元素相连,实现车站与区间的拓扑连接。

图3 铁路车站物理网络拓扑图Fig.3 Physical network topology of train stations
1.1.2 列车进路数据构建方法
为构建精细化列车径路表达,径路在各车站内的走行过程以基于车站(车场)拓扑结构的列车进路数据描述。进路是由若干个信号机、道岔及道岔位置、轨道区段组成的列车在车站内行车时所经过的通路,并可由始端按钮和终端按钮决定进路的相关信息[17]。根据按钮使用规则[18],即可确定车站内可组成基本进路的始终端信号机组合,进而生成车站内的列车基本进路数据。基于图2 车站站型,根据进路按钮组合XLA、S3LA(LA 为按钮标识),即可确定一个简单的接车进路(X,1,5,S3,3G)。
列车进路可作为车站进出口连通拓扑的数据支撑,同时也可作为径路搜索下的列车站内走行可视化展示,根据上文构建车站物理网络拓扑,参考联锁车站联锁图表编制原则[19],通过采用遍历算法生成车站的列车进路数据,算法简述如下。
步骤1:遍历车站的列车信号机,作为进路起始信号按钮,依次在车站物理网络拓扑邻接矩阵中进行检索。
步骤2:查找并遍历与起始信号按钮相连的拓扑元素并递推至信号类型的拓扑元素,若该信号可作为终端按钮,遍历并记录经由不同的所有进路道岔信息、终端信号按钮及关联股道;若不可作为终端按钮,则继续递推至下一个信号或直到无解情况。
步骤3:判断迂回进路。遍历各进路的道岔顺序编号,如道岔顺序x,y,z可由数位更少的x,z连通,则包含x,y,z道岔顺序的进路标记为迂回进路。
步骤4:算法结束。
1.1.3 车站进出口连通拓扑构建方法
基于列车进路数据描述车站进出口间的拓扑关系,即构建车站层级连通拓扑。基于图2 车站站型,根据存在X-S3(3G)和X3(3G)-SN的列车进路,可构建车站进出口ENT1(X)-ENT3(SN)的连通关系。
考虑车站车场和线路所等车站拓扑结构,按进出口的位置及连通关系主要分为以下几类,车站层级进出口连通图如图4所示,①→②可表示不过股道转场路径;③→④可表示过股道的转场路径;⑤→⑥可表示过股道的通过路径;⑤→⑦可表示同侧到发的折返路径;⑩→⑨可表示不过股道的线路所通过路径。综合上述各类情况可知,若车场间有列车径路行驶条件,且无场间进站信号,可于转场道岔处设置虚拟信号,便于生成转场进路;不经过股道的进出口间的路径可由一条进路或多条分段进路表示,过股道的进出口间的路径可由与该股道相关的2 条进路或多条分段进路表示,综合考虑同侧到发的折返路径等问题,设计基于列车进路数据的车站进出口拓扑图算法实现过程如下。
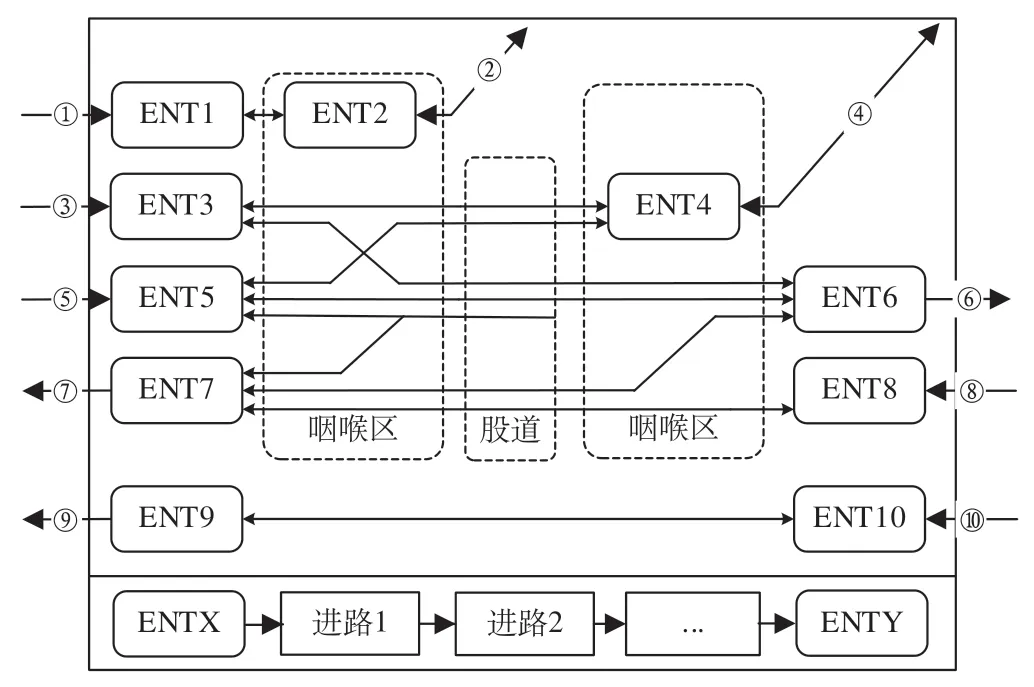
图4 车站层级进出口连通图Fig.4 Entrance and exit connectivity at the station level
步骤1:遍历车站的进出口,提取与进出口相连的按钮信号,检索以该信号为始端按钮信号的基本进路。
步骤2:记录各进路的关联股道于集合V1,转步骤4;若进路无关联股道,将进路终端按钮信号记录于集合V2,转步骤3。
步骤3:若V2中信号与车站进出口相连,则记录进出口间存在连通关系;否则检索以该信号为始端按钮信号的分段进路,返回步骤2。
步骤4:遍历车站进出口,进行如下判定:①连通性判定。对比各进出口的集合V1,若存在相同股道,则记录进出口间的连通关系。②车站同侧到发判定。对比进出口间的接车进路终端按钮信号与发车进路始端按钮信号,若相同,则记录进出口间为同侧到发。
步骤5:算法结束。
1.2 路网层级连通拓扑构建及径路表达
基于高速铁路网干支线、站间联络线、场间联络线等区间信息,构建基于车站(车场)进出口的区间有向连通图,路网层级车站进出口的连通图如图5所示,线路所C的区间起始点ENT5与车站B的区间结束点ENT1 通过区间联络线相连。结合车站层级连通情况可以看出,基于车站进出口的连通图可分为站内连通和区间连通,前者主要影响径路线路选择,可以判断出车站转场、跨线、立折等列车行车条件,避免径路解空间内的不可行解;后者主要影响整体径路的权值,如区间长度、区间运行时分等,精细化径路搜索算法求解结果即为列车的实际具有运行条件的路径,求解过程更为高效。
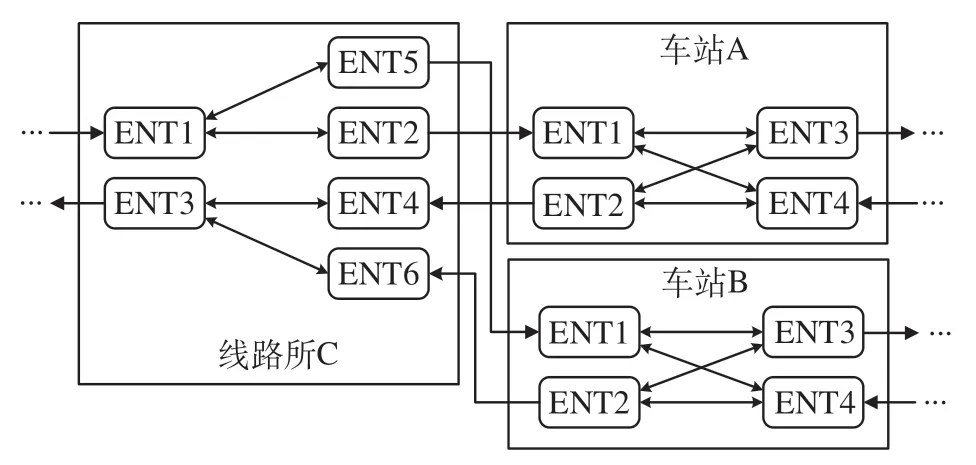
图5 路网层级车站进出口的连通图Fig.5 Entrance and exit connectivity at the railway network level
高速铁路网为稀疏连通网络,节点较多,但节点的连通数量较少,因此选取以车站进出口为节点的邻接表模型,并对邻接表数据进一步处理和优化,提升算法搜索效率,将区间连通关系合并处理。基于车站进出口的高速铁路网邻接连通关系描述为:车站A 进出口a1→车站A 进出口a2(→车站B 进出口b1),以图5 为例,线路所C 的1 接口邻接表可表示为C1[C2(A1),C5(B1)]。实现算法如下。
步骤1:遍历车站进出口,根据区间上下行方向提取与进站方向(区间结束点)相连的进出口,作为邻接表的表头节点元素。
步骤2:遍历邻接表的表头元素,检索存在拓扑关系且与出站方向(区间起始点)相连的同站进出口,记录邻接关系。
步骤3:遍历各出站方向的车站进出口,检索得到具有区间拓扑关系的另一个车站进出口(区间结束点),记录邻接关系。
步骤4:算法结束。
通过构建车站物理网络拓扑生成列车进路表,再由列车进路数据构建基于车站进出口的站内拓扑网络,结合路网区间等数据构建基于车站进出口的多维度高速铁路拓扑网,实现车站或车场内线路连通判断、径路是否存在同方向到发、径路搜索结果的站内路径展示等,支持更精细化的径路搜索结果。
2 基于A*的高速铁路网多径路搜索算法研究
2.1 多维度路径搜索参数设计
基于车站进出口的多维度路径包括车站层级连通关系及路网层级连通关系,需要对构建的精细化高速铁路拓扑网的车站、车场、线路、区间等信息进行统一的编码设计,涉及车站经纬度、车站车场关系、进路、车站进出口等数据,以满足路网数据的规范化存储、路径表达,以及准确高效计算,便于实现多径路搜索算法。
(1)车站经纬度数据。定义车站列表V[v1,lon,lat],分别表示车站编号、经度、纬度。
(2)车站车场关系数据。定义车站vi的车场集合若车站无分场,
(3)车站进路数据。定义车站车场的一条进路j集合为分别表示进路起始信号按钮、所经道岔(以集合SW表示)、结束信号按钮、关联股道。
(4)线路属性数据。定义线路集合L[li,tp,sv],分别表示线路编号、线路类型、线路设计速度。
(5)车站进出口数据。定义车站车场的进出口ek集合[e1,e2,…]。
(6)区间属性数据。定义线路li的区间j集合即区间的起始车站车场的车站进出口为est,结束车站的车站进出口为efn;dir为区间单双向行车类型;phe(l,t)为区间长度、区间运行时分。
(7)基于车站进出口的邻接表例如ex存在站内的连通关系ea,通过区间EL与车站车场的车站进出口eb相连。按同方向到发的进出口是否连通可分为,。
2.2 路网分层优化
高速铁路中间站节点连接关系简单,数目较多,具有路网拓扑简化的技术条件,通过对邻接表模型进行优化,对节点进行分层处理,快速检索。通过遍历邻接表R,提取进出口连接数量大于等于2(len≥2)的节点组成点集合V*,合并节点间区间E及邻接关系R*,重构组成高层简化路网G*=(V*,E*,R*)。针对位于底层路网的源vx、汇vy,构建Gx,y进行径路搜索,构建算法如下。
步骤1:初始化,令Gx,y=G*。
步骤2:检索源vx的车站进出口的径路,在底层路网G内按上、下行分别推算至高层路网G*中的车站时截止,得到2 个低层路网,,将其加入Gx,y。
步骤3:检索汇vy车站进出口的径路,同理可得到2个低层路网,,将其加入Gx,y。步骤4:算法结束,得到
2.3 基于A*算法的k短路径路算法
高速铁路物理网络节点、边数目大,枢纽地区网络连接结构复杂,采用传统的遍历算法计算效率较低。A*算法是一种常用的启发式搜索算法,搜索过程中各节点的目标函数如下,由起始搜索节点至当前节点的计算值、当前节点至结束节点的估值组成。
Nilsson 等人在1968 年证明A*算法的3 个重要性质:若路径规划问题存在有效路径,A*算法必能找到该解路径;A*算法能够最有效地利用启发式,即在使用相同启发式时,没有一种搜索算法的搜索空间比A*算法小;A*算法收敛效果与启发式函数有关,当启发式函数值h(x)小于等于其实际代价h*(x)时,必能找到最优解路径;当启发式函数等于实际代价,可更快速度收敛至最优解。
2.3.1 最短路径路搜索
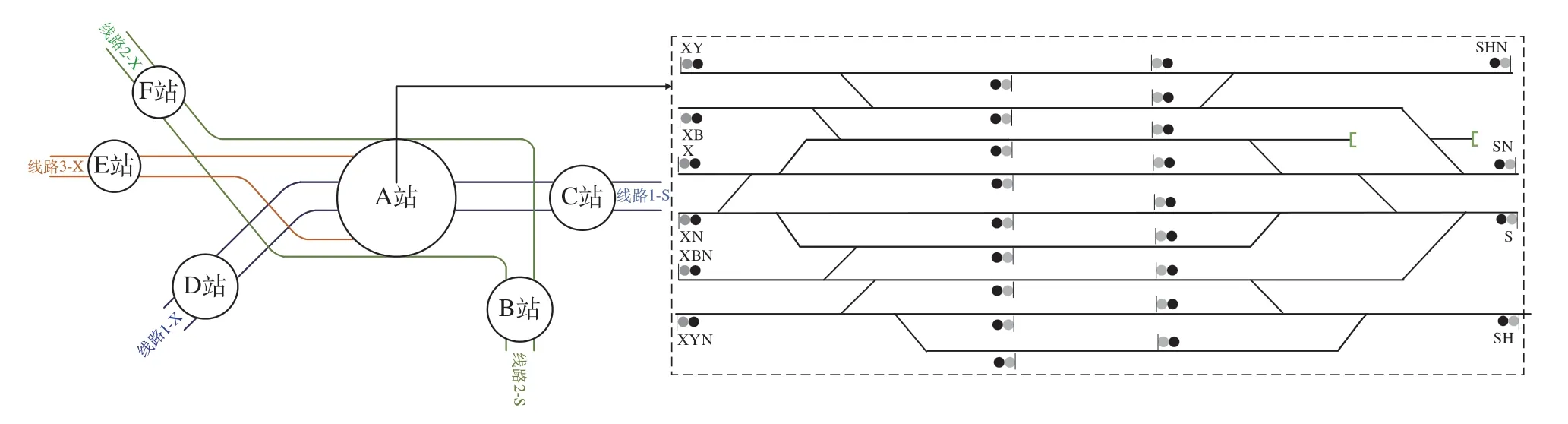
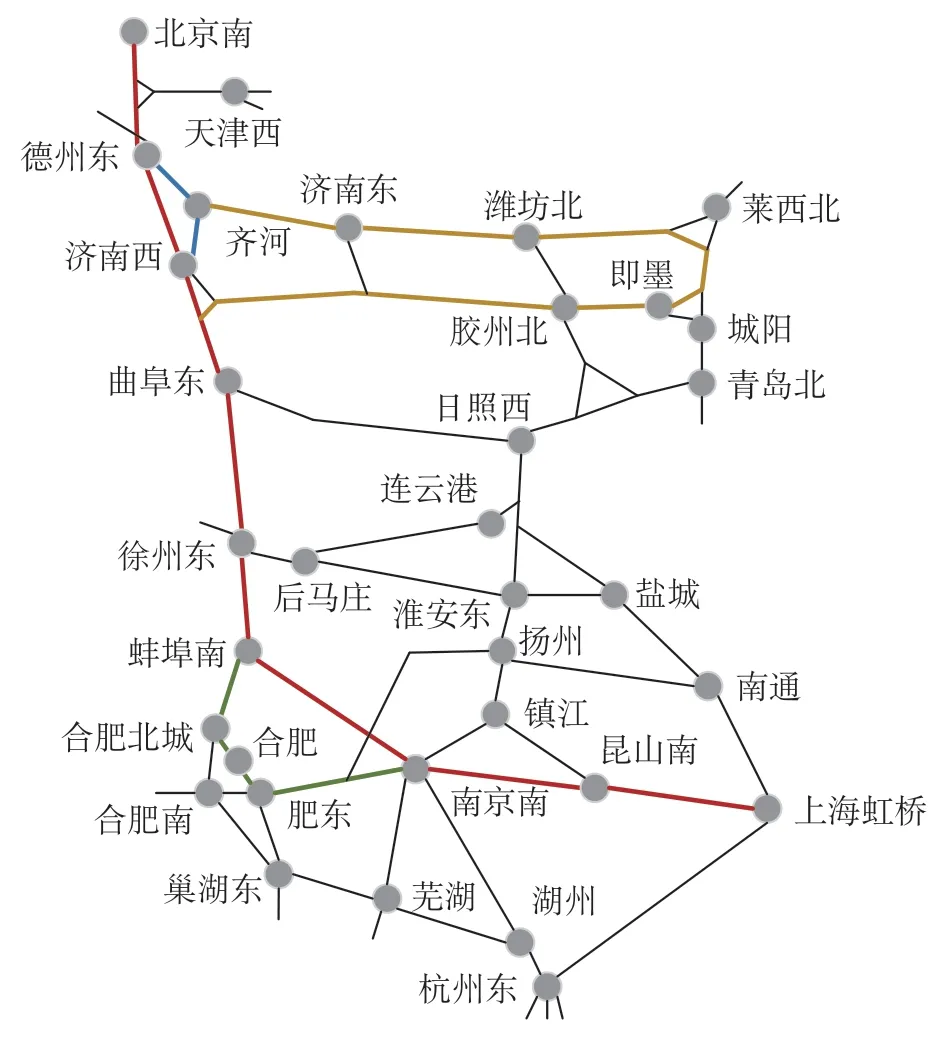
启发函数h(x)需根据具体问题来设置,高速铁路网径路边的权值h*(x) 主要由区间长度[phe(l,t)]确定,显然以节点之间的直线距离作为启发函数h(x),可满足h(x) 利用标准A*搜索算法,可缩减搜索范围,最大程度减少无效搜索的时间开销,提升搜索效率,实现最短径路的快速搜索,算法详细流程不再赘述。 2.3.2 多径路搜索 多径路搜索可用Dijkstra 算得的最短路作为启发函数。对于源vx、汇vy的路网Gx,y,以汇vy为起始节点对路网进行Dijkstra 运算,得到路网内任意节点vi至汇vy的最短路径dis(xi,y),此时启发函数h(xi,y)=dis(xi,y)=h*(xi,y),算法收敛速度快且可得到K短路最优解。 以DRC[vi].[,vi,f,g,h,Vroute,Eroute,Rroute]存储搜索过程中节点vi的径路信息于OPEN 或CLOSE列表中,其元素分别表示搜索过程中vi节点的前续父节点、当前节点、f值、g值、h值、所经节点集合、所经边集合、所经节点连接关系集合。基于A*的多径路搜索流程图如图6所示,算法步骤如下。 图6 基于A*的多径路搜索流程图Fig.6 Flowchart of multi-route search based on A* algorithm 步骤1:对于源vx、汇vy,检索其是否位于高层路网G*,若节点不满足,则按2.3 节路网简化算法构建Gx,y。 步骤2:初始化待扩展节点集合OPEN 列表、已扩展节点集合CLOSE 列表;将起始节点的径路信息DRC放入OPEN列表中,令k= 0。 步骤3:当k≤K时,若OPEN 列表不为空,转步骤4,否则表示问题无k个最短路,算法结束;当k>K时,转步骤7,输出k短路解。 步骤4:遍历OPEN 列表的节点vi,提取f值最小的节点记为v*,将v*从OPEN列表中删除,并放入CLOSE集合中。 步骤5:判断v*是否为终点,若是则得到问题的一个k短路解,k=k+ 1,转步骤3;若v*不是终点,则对该节点进行邻域拓展,得到有关v*的一系列后继节点vi,若vi∈DRC[v*].[Vroute],则说明包含环形径路,不再进行邻域拓展;对于所有其余vi计算DRC[vi]径路信息并添加于OPEN 集合(集合中可能存在前续父节点不同的同名vi节点,即k短路下不同径路搜索过程)。 ①标记vi的前续节点v* =DRC[vi].[]。 ②计算DRC[vi].[g]=DRC[v*].[g]+e,e为vi与前续节点间路径的权值;计算DRC[vi].[h]=dis(vi,y);DRC[vi].[f]=DRC[vi].[g]+DRC[vi].[g]。 ③更新vi的节点、边和连接关系集合,如DRC[vi].[Vroute]=DRC[v*].[Vroute]+vi。 步骤6:完成v*的所有后继节点vi检查后,转步骤3。 步骤7:根据节点的节点、边和连接关系集合,描述k短路径解。 研究建立了基于车站进出口的多维度高速铁路拓扑网,包括车站层级拓扑及路网层级拓扑2 部分,下面分别从上述2方面展开实例验证。车站拓扑方面,枢纽内客运站一般有多条线路衔接,连接关系复杂,研究以一个小型枢纽实例验证高精度高速铁路站内拓扑网的准确性,A,B等6个站组成的小型枢纽仿真实例如图7所示。其中A站衔接有3条线路、上下行共计10个延伸方向,其余车站均为中间站。 图7 小型枢纽仿真实例Fig.7 Simulation example of small railway hub 根据车站拓扑结构,通过列车进路生成算法、车站进出口拓扑生成算法、路网邻接表拓扑算法等,计算A 站与B,C 等站的连通性,并与基于车站节点连通关系的中观路网径路求解进行对比分析,不同路网精度下径路搜索结果对比如表2 所示。通过对比分析可得知,基于车站进出口的高精度径路搜索在车站层级是可行、有效的,且径路结果展示、车站内线路连通性判定、车站内同方向到发判定等方面精度更高。 表2 不同路网精度下径路搜索结果对比Tab.2 Comparison of route search results under different precision of railway networks 以截至2022 年底我国高速铁路网为例,构建高精度高速铁路网连通拓扑图,对北京南高速场—上海虹桥高速场的列车径路进行分析,在不考虑同侧到发折返作业的情况下,北京南高速场至上海虹桥高速场前5 条最短路如表3 所示,北京南高速场至上海虹桥高速场前5条最短路示意图如图8所示,径路联络线信息不在表中展示。由结果可看出最短路全程为京沪高速铁路(北京南—上海虹桥);次短路在德州东与济南西间走石济客专(德州东—齐河)线路;徐盐(徐州东—盐城)、连镇客专(董集—丹徒)方向无可行k短路,因为径路仅能通达至上海虹桥综合场。高精度路网下最短路求解耗时300 ms左右,k短路求解时间受OD及k值影响有一定波动,可以实现高效、准确地完成精细化的路网径路搜索。 图8 北京南高速场至上海虹桥高速场前5条最短路示意图Fig.8 First five shortest routes from Beijingnan high speed railway yard to Shanghai Hongqiao high speed railway yard 表3 北京南高速场至上海虹桥高速场前5条最短路Tab.3 First five shortest routes from Beijingnan high speed railway yard to Shanghai Hongqiao high speed railway yard 研究针对大规模复杂高速铁路网,考虑线路区间信息、站场结构以及站内进路信息,构建基于车站进出口的复杂拓扑网络及多维度路径信息表示方法,设计基于启发式A*算法的考虑精细化站场结构的多径路搜索算法。实例验证表明,该方法可以求解复杂路网条件下高速铁路列车运行精细化径路,为高速铁路列车运输组织工作提供技术支持。
3 实例验证


4 结束语

