基于增强模拟退火算法的动车所调车作业计划多目标优化方法
刘 毅,唐秋华,何 明
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,湖北 武汉 430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
0 引言
动车运用所调车作业计划是进行动车组清洗、检修等基础维护作业的行动指南。合理编制调车作业计划可极大提升动车所的作业安全性与使用效率。目前,动车所在实际作业过程中,常由于调车作业计划不合理,导致作业股道、咽喉区被无效占用,使得待检修动车组长时间等待或进行过多非必要转线。因此,亟需合理编制动车组调车作业计划,提高资源利用率,减少无效等待时间。
针对该问题,殷迪等[1]构建了整数规划模型,童佳楠等[2]将其转换为具有特殊过程约束的混合流水作业车间调度问题。史锦堂等[3]重点考虑灵活存车和列位占用问题。户佐安等[4]建立了考虑股道列位占用的动车所调车作业计划编制优化模型。张惟皎等[5]重点考虑存车线的列位占用问题,建立存车线运用优化模型。以上研究多聚焦于列位占用、总作业时长等单目标优化问题,忽略了实际作业往往具有多个互相冲突的目标。例如,动车组在转换作业区时需要进行股道间转线,转线所跨越的股道数量越多,调车作业的耗时和费用也将越大,转线复杂度越高。此外,以上研究在作业模式上,主要考虑需要清洗、检修2 项任务的作业类型,而未考虑仅需进行检修作业的动车组在计划中的作业安排。因此,需要在常规目标基础上,另行考虑转线复杂度的影响,同时在计划编制中,增加仅检修的作业模式,提升调车计划的实际性。
在求解方法方面,已有文献主要采用遗传算法(GA)、粒子群算法(PSO)等群智能算法。其中,韩宝明等[6]提出一种改进遗传算法,用以求解动车所一级修灵活作业顺序的非线性整数模型。王家喜等[7]以调车总钩数最少为目标,利用粒子群优化算法求解。与群智能算法相比,局部搜索算法更加关注问题特点、参数较少且鲁棒性强,亦可用于求解动车所调车作业计划多目标优化问题。
据此,提出一种增强模拟退火算法,通过设计基于启发式规则的解码策略及基于归档集的重启机制[8],用以求解以动车所调车作业时间最小化、调车作业转线复杂度最小化为目标的多目标优化问题。
1 问题描述
动车所按照其功能主要包括存车区、清洗区、检修区、辅助股道等部分,多采用尽头式布局方式,各区域之间通过咽喉区相连,构成完整的动车所检修系统。动车组在完成当日载客任务后,进入存车区,根据清洗区和检修区的使用情况选择下一步作业;完成全部作业任务后,返回存车区待命。若下一步作业的所有股道均被占用或下一步作业所在区域与当前作业区之间咽喉区转线股道被占用,则只能在原位置等待,直至上述2 个条件均已满足,才能继续进行作业。尽头式动车所如图1所示。
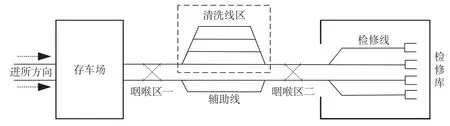
图1 尽头式动车所Fig.1 Stub-end EMU depot
咽喉区存在于动车所相邻作业区之间,内部汇聚道岔等转线设备,是动车组进行作业区转换的必经之路。咽喉区股道同其他作业股道均具有独占性,但不允许等待,动车组需按时通过,进入下一工序。为简化问题,将每个咽喉区处理为一条特殊的作业股道,其操作时长等于转线时长。咽喉区股道运用频率极高,在时间和空间维度都可能存在不相容性,因而是动车所作业编制问题中的重难点。此外,动车组在进行不同作业区之间转换时,需通过咽喉区股道进行转线,动车组转线需要调动人员、设备等多方面资源[9]。转线所跨越股道的数目增加会使调车作业的难度和资源消耗增大,不合理的转线方案也会降低动车组在作业区之间转换的安全性[10]。
由此,动车所调车作业计划优化问题可总结为:在动车所设备资源、布局等前提确定情况下,编制可行的动车所调车作业计划,力求获得更小的总调车作业时间及更低的转线复杂度。
2 数学模型
该问题需同时优化调车作业计划总时间、转线复杂度2 个目标,基于此构建多目标优化模型。符号说明如表1所示。

表1 符号说明Tab.1 Symbol description
2.1 目标函数
动车组进所后,按照调车作业计划完成任务,进入存车区等候出所。总作业时间越短,在存车区等候时间越长,则该计划的鲁棒性越强;采用调车作业计划的转线所跨越股道总数量化转线复杂度。降低作业计划的转线复杂度,调车作业的难度与费用也会降低。据此,多目标函数由公式⑴—⑵组成。
公式⑴表示最小调车作业计划总作业时间;公式⑵表示最小调车作业计划转线复杂度。
2.2 优化模型
对股道分配进行约束。
公式⑶表示可变作业模式动车组须从A,B两种作业模式选择一种作业模式。
公式⑷表示选定作业模式后,每个阶段的操作 需在指定作业区内进行。
公式⑸—⑹表示任一股道上的作业需按先后顺序分配,且每一位置上最多只能分配一个任务。
对时序逻辑进行约束。
公式⑺表示股道d上第g+ 1项操作的开始时刻不得早于其第g项操作的结束时刻。
公式⑻—⑼表示动车组e第s个作业的结束时刻大于其开始时刻加上该作业区的标准作业时间;完成任务后原地等待转线。
公式⑽—⑾表示动车组e第s个作业步骤的结束时刻加上标准转线时间,等于其第s+1 个作业步骤的开始时刻。
公式⑿—⒀表示股道d上进行的第g项操作开始 时刻等于所分配的动车组e第s个作业的开始时刻。
公式⒁—⒂表示股道d上进行的第g项操作结束时刻等于所分配动车组e第s个作业的结束时刻。
3 增强模拟退火算法
动车所调车作业计划编制问题包含时间和空间多维约束条件,影响因素多[11];随着动车组数目的增加,求解难度逐步增大,属于NP-hard 问题。在实际工作中,传统人工编制方法并不能满足检修计划对于速度和安全性的实际需求,因而拟采用智能优化算法对该问题进行求解[12]。考虑到模拟退火算法具有参数较少、鲁棒性强、适用于求解复杂非线性优化问题的特点,选用其作为优化算法,并结合问题特征进行改进,以获得更好的求解效果。
3.1 编码及初始化
3.1.1 问题编码
解的编码策略如图2 所示,调车作业计划编码由2 段长度为动车组列数的字符串组成,第一串对应于决策变量Xe,l,表示各动车组的检修模式,只能是A,B,C 3种模式中的一种。第二串为各动车组的作业先后顺序。

图2 解的编码策略Fig.2 Encoding strategy of solutions
3.1.2 基于入所时间的初始化
初始解性能对局部搜索算法求解速度影响较大,而随机初始化会使得初始解质量较差,需进行适当改善[13]。为此,针对作业顺序排序,设定先进入存车区的车辆在各作业区具备更高的作业优先权,便于及早完成检修任务,回归存车区待命;同时还能最小化各动车组在动车所的作业流程时间,减少冲突与无效等待时间,使得各动车组能够提前做好出所准备。
3.2 基于组合启发式规则的解码设计
动车所调车作业计划编制约束复杂,在解码时易造成股道分配冲突,导致解不可行,求解效率极低[14]。因此,拟设计组合启发式规则,通过明晰空闲股道选择方式、同一股道上的冲突消解方式,在给定编码前提下获得性能较优的解。
3.2.1 股道分配规则
在动车组进行作业区间转换时,为明确股道分配方式,并避免无效的股道变换,导致转线复杂度上升,设计股道分配规则进行约束。
在对任意动车组e的下一项作业进行股道分配时,检查作业区r所有股道DR当前占用情况,并找出最早空闲股道分配给e;若此时无空闲股道,需使该动车组在当前作业股道等待,直至下一项作业区存在空闲股道;当有多条空闲股道同时存在时,考虑作业区股道布置采用近似对称的方式,各作业区通过咽喉区股道相连;咽喉区股道视为一条特殊股道,处于动车所布局中轴线上。因此,在为某动车组e分配作业股道时,优先分配靠近中轴线的股道,以减少动车组转换作业区时跨越的股道数量、降低转线复杂度,采用以下方式选择转线复杂度最小股道作为目标股道。
设定咽喉区股道所处位置为中轴线,则其距离中轴线的偏差值为0。计算其余股道与中轴线的偏差值,并据此进行股道选择。首先遍历该作业区z的所有股道,筛选出所有空闲股道,然后依据公式⒃优先选择股道偏差最小的股道d‘,并将该股道分配给动车组e。若多条股道存在相同股道偏差,则随机选择其中一条股道作为待分配股道。
3.2.2 冲突消解规则
动车所调车作业冲突现象主要是由于计划编制的不合理性,造成2 列或多列动车组在安排至相同作业股道的工作时间存在冲突,致使计划不可行[15]。由于我国动车所多采用尽头式布局,在调车作业上存在折返性,以存车区为起始点,检修区为终止点。动车组行进方向为检修区定义为正向,行进方向为存车区定义为反向。冲突可能由正向或反向的多列动车组造成。针对该现象,设计相应冲突消解规则进行解决。
若动车组Ne与Ne+1在股道d上存在冲突,判断两动车组的行进方向,若均为同一方向,比较两动车组在该股道进行作业的起始时间Ie,s和Ie+1,s,若Ie,s 3.2.3 基于组合启发式规则的解码流程 在前述规则基础上,解码步骤如下。 步骤1:获得一个解,如{(B,A,B,A,C,B,C,B),(3,2,5,4,1,7,8,6)}。 步骤2:运用股道分配规则给动车组分配相应股道。 步骤3:判断冲突。①判断该解是否存在冲突情况;②若存在,使用冲突消解规则;若不存在,转步骤4。 步骤4:生成一个可行的调车作业计划。 针对解的编码方式,通过两种邻域搜索方式,来保证算法解的可行性和多样性。 (1)针对作业顺序编码,随机选择编码中相邻两点,交换其作业顺序与作业模式。 (2)针对检修模式编码,随机选择编码中一点,若其作业模式为先清洗后检修,则变为先检修后清洗,反之亦然。仅检修作业模式由于其固定的作业属性,不参与该邻域搜索。 由于算法需要同时考虑调车作业最小总时间和最小转线复杂度2 个优化目标,因而引用Pareto 优化概念,通过个体间的支配关系判断解的优劣程度,均衡各目标解之间的关系。对于某一解Scurrent,若其他解均无法支配该解,则称Scurrent为一个非支配解,所有的非支配解放入归档集中,定义为F。关于归档集更新,若通过邻域结构变化产生的新解Snew,可支配归档集F中任意一个解Si,则将Snew放入归档集,并删除归档集中所有可支配解,构成新的非支配解归档集。 模拟退火属于局部搜索算法,在求解问题时,为避免陷入局部最优解,使归档集中解的分布更优,设定重启触发参数dn=0,Dn为启动重启机制的临界值。考虑问题规模对算法获得更优解的影响,取Dn=Ne∕2,其中Ne为动车组数量。当连续迭代次数超过Dn次而未更新归档集时,即dn>Dn时,触发重启机制,选取归档集中最优个体解作为算法当前解开始迭代。最优个体解通过使用擂台赛法则对每一代中归档集进行计算获得。 改进多目标模拟退火算法流程图如图3 所示。首先,输入当日各动车组运用计划、各作业区标准作业时间等相关数据。算法开始,产生初始解。随后通过启发式规则进行解码,并通过邻域搜索更新获得新解。在更新解的过程中,采用改进收敛准则接受劣解;若出现非支配解,更新归档集;当满足重启条件时对算法进行重启。满足终止条件后,算法结束,输出归档集并获得最终调车作业计划方案。 图3 改进多目标模拟退火算法流程图Fig.3 Procedure of multi-objective simulated annealing algorithm 某动车运用所某日动车组运用计划案例如表2所示,其中D8 列动车组为仅检修模式,其余动车组需进行清洗、检修2 项任务。建立多类型股道资源案例如表3 所示。在下述实验中,各作业区标准作业时间为:清洗区p1= 5 min,咽喉区股道p2=p5= 6 min,清洗区p3= 60 min,辅助股道p4= 4 min,检修区p6= 150 min,且各工作区作业时间固定不变。 表2 动车组运用计划案例Tab.2 EMU rescheduling cases 表3 股道资源案例Tab.3 Track resource case 经过多次实验比较,采用T0=15 000,Maxgen=150,Alpfa=0.9,LK=30作为实验参数,所提EMOSA算法的求解效果最佳。 相较原始多目标模拟退火算法,所提算法主要改进包括基于启发式规则的解码流程、与问题规模相关联的重启机制。为验证改进算子的有效性,将原始多目标模拟退火算法、仅加入解码设计策略、仅加入重启机制、同时加入所有改进的4 种算法分别命名为MOSA,MOSA_Re,MOSA_De,EMOSA,采用逆世代距离和超体积比率作为评价指标进行性能比较。 其中, 逆世代距离(Inverted Generational Distance,IGD)通过计算目标算法获得的解与最优非支配解集之间的距离,以判断算法的收敛性和多样性。如公式⒄所示,最优非支配解包含所有测试算法结果中的非支配解。IGD值越接近于0,则表示解的收敛性和多样性越好。 式中:dtj表示最优非支配解集中的解j到目标算法获得的解中距离最近解的欧式距离;|TP|表示最优非支配解集中解的数量。 超体积比率(Hyper volume Ratio,HVR)表示所求目标算法Pareto 解集与参考点w的超体积占最优非支配解集边界与参考点w的超体积的比值,如公式⒅所示。获得的HVR值越接近1,表示解越接近真正的边界,算法综合性能越好。 式中:n为目标算法获得的解的个数;m为算法获得最优非支配解集的个数;vi为第i个超立方体。 为保证案例多样性及满足不同规模动车组对于最小股道资源的需求,通过改变动车组数目及股道资源状态,来获取不同规模案例,将表3 中前8,前9直至前11列动车组分别作为独立运用计划案例与表4股道类型Ⅰ-Ⅴ、Ⅱ-Ⅵ、Ⅲ-Ⅷ、Ⅵ-Ⅸ进行逐一组合,总计生成20 个不同规模的实验案例。对每个案例独立运行10 次的指标均值进行统计,改进算子有效性实验中IGD,HVR值的95%置信区间如图4所示。 表4 动车组在各线区作业起止时间Tab.4 Starting and ending time of EMU operation in each line area 图4 改进算子有效性实验中IGD、HVR值的95%置信区间Fig.4 95% confidence intervals of IGD, HVR values from validity tests for the improvement strategies 实验结果显示,融合2 种改进算子的EMOSA算法在两项评价指标中表现均为最优,即意味着该算法改进点能够有效针对动车所调车作业计划问题的特性,所得非支配解集收敛性强,拥有更好的鲁棒性及多样性,可以更快速获得优质计划方案;两种具有单一改进算子的算法相较于原始MOSA算法也均获得了性能提升。重启机制以动车组数目作为阈值,保证其运用频率适当,有效避免算法陷入局部最优解。基于启发式规则的解码设计提升算法性能的原因为:①冲突消解规则可以消解股道冲突,提升解的多样性,剔除不可行解;②股道分配规则可以引导股道分配方案向积极方向进行优化,减少随机性,提升寻优效率。 某动车运用所某日实际运用计划如表2 中D1—D10 所示,其中D8 列动车组仅需进行检修作业,该动车所的检修设备数量如表3 中类型Ⅲ所示,采用近似对称布局,因此以存车线4—咽喉区1—清洗线1—咽喉区2—检修线3 作为动车所中轴线,用以统计调车作业中转线所跨越股道数量。采用所提EMOSA 算法对该日调车作业进行计划编制。动车组在各线区作业起止时间如表4 所示,对应的股道占用甘特图如图5所示。 图5 股道占用甘特图Fig.5 Gantt chart of track occupancy 由结果可知,本算例调车作业计划的总作业时长为2 751 min,总转线跨越股道数仅为93 条。动车所各作业区设备资源得到均衡合理利用。各列动车组均在运用计划规定发车时间前完成各项检修任务,且预留充足时间在存车区待命,以提高应对各类临时突发状况的能力。通过所提算法获得该作业计划,求解时间仅为3.5 s,相较于目前动车所采用的人工编制调车作业计划方式,可大幅缩减计划编制时间,同时提升计划方案的可靠性和实用性。由此,证明所提模型及算法能够有效针对动车运用所调车作业计划编制的特性与难点,合理避免股道占用冲突,快速稳定地编制出可行调车作业计划方案,同时有效降低调车作业转线复杂度,缩短总作业时间,从而提高动车运用所的资源使用效率,降低调度人员的工作量,提升动车运用所的经济效益。 针对带有咽喉区股道约束的尽头式布局动车所调车作业计划编制问题,将仅检修作业模式考虑在内,以最小作业时间和最小转线复杂度为目标,提出了一种增强多目标模拟退火算法,其中包含2 种改进措施:基于启发式规则的解码设计,帮助算法获得性能较优的解;与问题规模相关的帕累托前沿解集重启机制,帮助算法跳出局部最优解。采用不同规模的多个案例,验证了改进算子的有效性,并以某动车运用所为例,验证了模型和算法的可行性和合理性。未来研究可考虑多列位情况下动车所调车作业计划编制问题。3.3 邻域搜索
3.4 基于Pareto的性能评价
3.5 基于归档集的重启机制
3.6 算法求解流程

4 实例分析


4.1 改进算子有效性验证
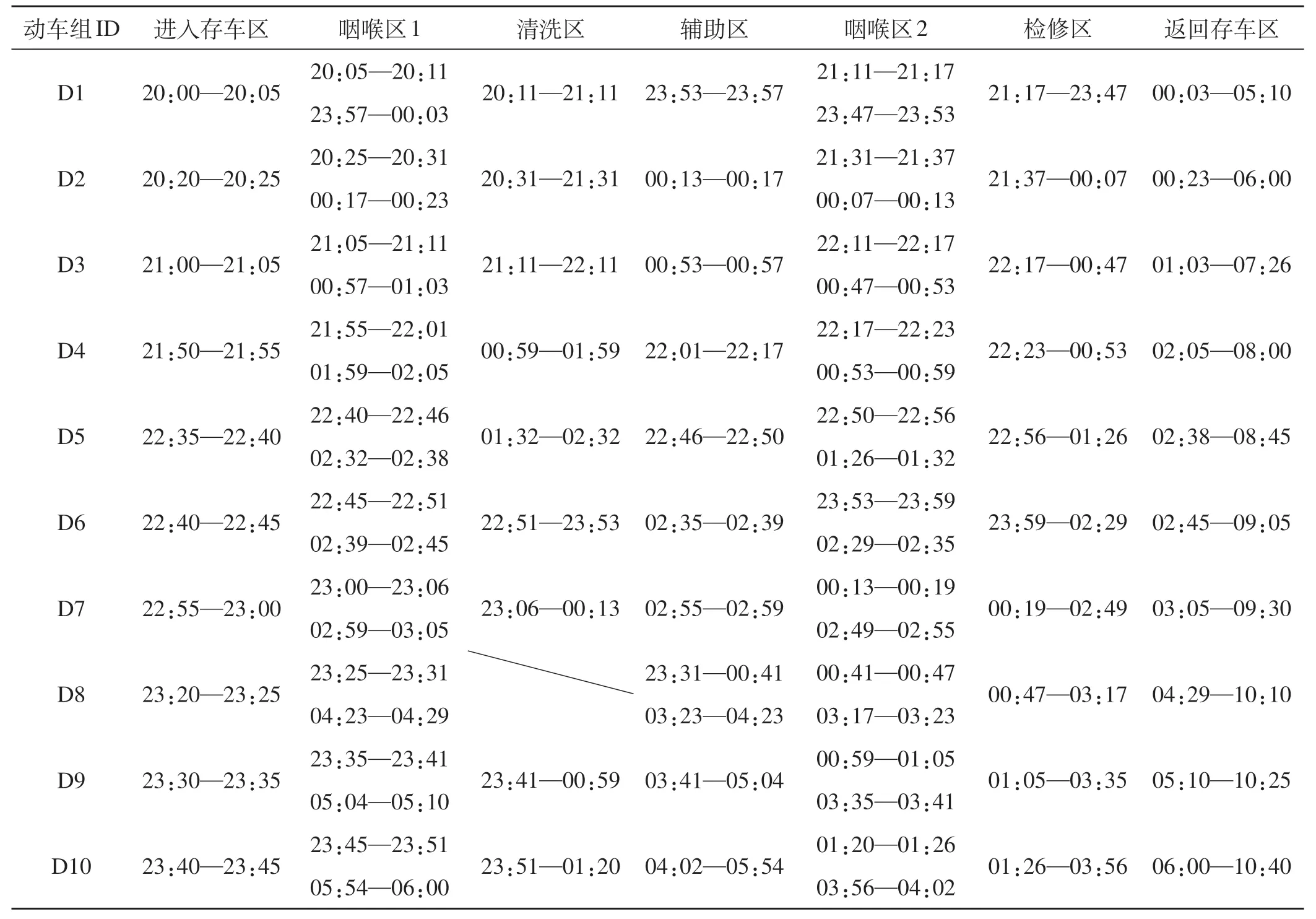

4.2 实际案例分析

5 结束语

