基于IQPSO-EKF的多传感器融合姿态测量方法研究*
胡启国,王 磊,马鉴望,任渝荣
(重庆交通大学 机电与车辆工程学院,重庆 400074)
0 引 言
竖井掘进设备工作环境狭隘,地面的测量方法如卫星定位、图像识别等无法使用。竖井掘进设备是否能按设计姿态运行,并且符合施工要求,首先要看姿态测量系统的精度能否满足设计要求。
当前国内外的隧道、井下施工中主要使用的姿态测量方法是以自动化测量为主,人工测量法为辅。人工测量法包括支撑杆法、直角三角形测量法、前后标尺法等。其中,前后标尺法测量为常用方法,测量过程中需要保证标尺的水平度和垂直度,不然将会严重影响测量精度[1]。自动测量法主要有视觉测量导向系统、棱镜导向系统、陀螺仪导向系统、激光标靶导向系统等方法。
其中,陀螺仪导向系统是利用陀螺仪与倾角仪相结合的方法,对掘进机进行姿态测量[2]。陀螺仪通过测量物体在不同方向上的旋转速度,计算出物体的姿态信息,倾角仪辅助测量综合解算以确定掘进机位置。陀螺仪导向系统具有高精度、高可靠性和高性能等特点,其可以提高设备的导向精度和机体稳定性,在竖井掘进方面有着广泛的应用前景[3]。陀螺仪导向系统中通常采用MEMS传感器,其具有体积占比小、质量轻、能耗低等特点,目前已经成为竖井主流姿态传感器设备。但由于受到传感器制造工艺、安装精度、工作环境的影响,MEMS传感器存在不可避免的漂移与测量误差,仅靠实验标定去除并不具有普适性[4]。
刘震等人[5]提出了一种改进的卡尔曼滤波算法,以减弱卡尔曼滤波过程中加速度对姿态角解算精度的影响。
张春宇等人[6]采用基函数神经网络算法对训练数据进行了训练和分类,以提高水下航行器的测量姿态精度。杨小平等人[7]采用了一种基于一维卷积神经网络与长期短期网络相结合的加速度误差补偿方法,以实现误差补偿目的。高俊强等人[8]讨论了前后标尺法的测量原理和盾构姿态计算方法,以分析姿态测量的最低精度。陈旭光等人[9]提出了一种动态的零值偏移误差补偿算法,以滤除陀螺仪的零值偏移误差,提高了陀螺仪的测量精度。NEKRSOV Y A等人[10]研究了振动、冲击和声学噪声对MEMS陀螺仪性能的影响,比较了惯性体悬架不同共振频率的陀螺仪特性,揭示了具有更高共振频率的传感器的优势。
以上研究者均对MEMS传感器姿态测量做了分析或提出了新的测量方法,以减小测量误差,但是这些方法平均误差均较大,精度稍有不足。
因此,笔者采用基于扩展卡尔曼滤波(EFK)的多传感器数据融合方法,以加速度计、磁力计传感器等为观测测量值,引入平均位置最优值来避免陷入局部最优的IQPSO-EFK算法,优化EKF的系统,测量噪声的协方差参数。
1 姿态测量与解算理论
姿态解算的主要过程是姿态数据采集,笔者采用MEMS传感器进行数据采集;姿态数据预处理,主要是对采集的数据进行去除噪、滤波、校准等;解算姿态角,即利用数学模型计算出物体的姿态角。姿态角解算法主要有欧拉角法、方向余弦法、四元数法等方法[11]。
竖井姿态测量系统由MEMS传感器、激光指向仪、位置灵敏探测器(position sensitive detector,PSD)等组成。MEMS传感器,安装于竖井掘进设备结构中心位置,用于测量竖井掘进设备横滚角、俯仰角与偏航角。激光指向仪垂直于竖井井筒轴线,安装于竖井井口处,PSD位置传感器安装于竖井掘进设备顶部,用于接收激光指向仪的激光信号。
其中,PSD传感器与激光指向仪利用光电效应来完成位置的测量任务。PSD传感器由一系列光敏元件(光电二极管或光敏电阻)组成,这些元件被布置在传感器的表面上形成一个二维阵列。当光线照射到PSD传感器上时,光敏元件会产生电流或电压信号,根据这些信号的强弱和相对位置的差异来测量Z轴的位移。
其硬件构架如图1所示。

图1 姿态测量系统硬件构架
2 姿态角解算法
定义坐标系是描述竖井掘进设备在竖井工作中姿态状态的基础。目前可参考现有飞行器的坐标系建立法,建立地面坐标系和机体坐标系。
地面坐标系原点可为地面任意一点,O-X指向正北方,O-Y指向正东方,O-Z垂直于地面,坐标系符合右手原则。机体坐标系以飞行器质心为原点,Oa-Xa指向飞行器地速方向,Oa-Za垂直机体轴线,Oa-Ya通过右手原则确定。飞行器位置可以通过机体自带的卫星定位系统获取[12]。但由于竖井特殊的工况环境,卫星定位系统不适用。
为此,笔者根据竖井掘进设备姿态特点,为了获取角度、位移偏移等姿态数据,参考飞行器坐标系建立方法,建立地面坐标系O-XYZ,其中O-Z平行于井筒轴线,通过传感器(MEMS、激光指向仪、PSD位置传感器等)建立机体坐标系Oa-XaYaZa,如图2所示。

图2 竖井姿态双坐标系
姿态角是用于描述机体在三维空间中的姿态状态的角度参数。分析竖井掘进设备地面坐标系与刚体坐标系之间的联系,可得到竖井掘进设备与地面坐标系的相对姿态[13]。
在图1中,用来表示竖井掘进设备的姿态角有:α(roll)横滚角;β(pitch)俯仰角;γ(yaw)偏航角。
欧拉角法的基本原理是三维空间坐标系,描述机体按一定次序进行三次旋转动作。此法简便、直观,容易理解。但由于三角函数的特点,欧拉角法在解算机体全姿态时,微分方程在特殊角度会出现奇异点[14]。
欧拉角坐标变化分为两个步骤:
1)初始时刻将地理坐标系O-XYZ和机体坐标系Oa-XaYaZa重合;2)机体坐标系严格依照转动顺序进行三次转动,其三次旋转角度顺序依次是α、β、γ。
上述三次旋转连起来,合并则有:

(1)

陀螺仪并非直接测量竖井掘进机的角度,而是测量设备角速度再转化为角度。
陀螺仪姿态角关系式如下:
(2)
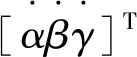
其中,当β=90°时,不能进行全姿态测量。
加速度计和磁力计的角度坐标系输出值分别是as=[axayaz]T和ms=[mxmymz]T。相对于参考坐标系处于静止状态或者匀速运动状态,参考坐标系下重力加速度的值为ar=[0 0g]T,单位向量是[0 0 1]T。
横滚角αa、俯仰角βa由加速度计求解得到,偏航角γm通过磁力计求解得到,可以表示为:
(3)
3 姿态数据处理
在实际姿态测量过程中,由于不可避免且不可控制的外界扰动,导致整个测量系统充满不确定性,易产生测量误差。目前,虽然尚未存在完美的建模方法来建立观测模型,但有较为接近其真实模型的估计方法。卡尔曼滤波器(Kalman filter)就是利用递推方式获得系统最小方差估计的方法[15-16]。
笔者利用MEMS陀螺仪的数据,建立卡尔曼滤波状态方程。因为状态方程呈现为非线性,所以必须采用非线性的扩展卡尔曼滤波算法(EKF)进行状态估计[17],即把状态方程中非线性系统线性化,即在真实点(线性化点)上展开为泰勒级数,省略二阶或更高,然后利用线性卡尔曼滤波对状态进行估计[18]。
在式(2)姿态角微分方程及运动学分析的基础上,可以构建卡尔曼滤波状态方程:

(4)
式中:Xk为时刻的理论值;k-1为上一时刻;μ为控制量;w为理论误差矩阵。
通过加速度与磁力计积分解出速度、位移为观测量,获得卡尔曼滤波观测方程:
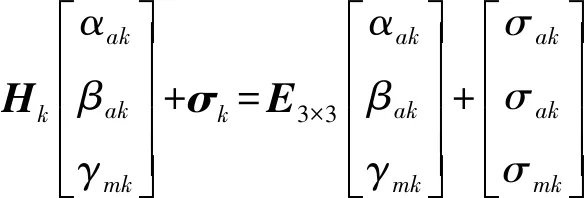
(5)
式中:Z为测量值;σ为测量误差矩阵。

令:
(6)
则Xk线性化为:
(7)

(8)
AJ、WkJ、HJ与VJ为雅克比矩阵,表达式如下:
(9)
扩展卡尔曼滤波算法预测矫正部分:
(10)


一般情况下,初始误差协方差应该尽可能接近实际系统的误差,而初始估计值应该尽可能接近实际系统的状态。另外,也可以通过实验来确定初始误差协方差和初始估计值,以获得更好的滤波效果。
4 粒子群算法分析和验证
对于状态方程与观测方程的初始参数估计不准确的问题,可采用最小二乘法、最小均方差法等方法进行合理估计。对于状态方程与观测方程的噪声误差协方差矩阵,即Q、R值,它们分别代表系统噪声和测量噪声的协方差矩阵,用来衡量系统噪声与测量噪声的大小[19]。一般情况下,Q、R的取值应该尽可能接近实际噪声的方差。而Q、R的取值也可以利用群智能算法寻参来确定,以获得更好的滤波效果[21-22]。

(11)

通过上述公式可以看出,Q、R的比值大小决定了Kk的大小,而Q或R绝对值的大小对Kk影响并不明显。因此,笔者应该权衡系统理论值与系统观测值的权重对Q、R进行设计。
粒子群算法易于实现,计算效率高,但存在早熟收敛的缺陷。学者们利用调控参数、引入退火算法、融合其他拟物类算法思想等方法,增加种群多样性,调高寻优速度,避免陷入局部最优的能力,提高其局部搜索能力,从而使其能够更精确、更稳定地解决众多优化问题。
孙俊等人[23-24]基于量子力学观点,提出了一种量子行为粒子群优化算法(QPSO),将量子力学不确定原理引入QPSO算法,即粒子更新不受粒子上一时刻位置与速度影响,增加了粒子位置的随机性。具有量子行为的粒子位置与速度是无法同时确定的。
粒子的位置迭代公式可以表示为:
(12)
式中:xid(t+1)为粒子t+1时刻的位置;u为[0,1]之间的随机数;Lai为局部吸引因子,由个体最优位置与全局最优位置确定。
Lai值的大小决定了粒子的搜索空间,Lai的具体表达式如下:
(13)
式中:φ为[0,1]之间的随机数;Pid为个体最优值;gd为全局最优值;c1,c2为权重值。
式(12)中β为压缩-扩张系数,其具体表达式如下:
(14)
式中:w1,w2为权重;itermax为最大迭代次数;t为当前迭代次数。
4.1 改进量子粒子群算法优化过程分析
群智能算法多以随机的方式初始化种群,但会造成种群分布不均,影响种群质量。因此,笔者借助混沌序列对QPSO种群进行初始化,利用混沌方程对初始种群进行优化,可实现种群的高随机性、均匀性等特点,高质量的初始种群可以进一步提高算法的收敛速度与寻优性能[25]。分段映射是通过调整p的取值对种群密度进行分段。
分段映射图如图3所示。

图3 分段映射迭代取值散点分布图
混沌方程如下:
(15)
其中:p∈(0,0.5];xN∈(0,1)。
Logistic映射的混沌状态,取决于u的取值。因此,笔者分别做了u=3.2,u=3.6,u=3.8时迭代1 000次的散点分布,其混沌方程为:
Xn+1=Xnu(1-Xn),u∈[0,4],Xn∈(0,1)
(16)
其散点分布图如图4所示。

图4 Logistic映射迭代取值散点分布图
由图4可看出:在u=3.2时,种群并不处于混沌状态,种群集中分布在两个区域;在u=3.6时,种群较为混沌,但其不均状态在多处区域并未分布;当u=3.8时,种群处于混沌均匀状态。
由于u的取值变化导致Logistic映射混沌状态的不稳定,而分段映射的参数设计简单且均匀性、混沌性要优于Logistic映射。因此,笔者采用分段混沌映射优化初始种群。
量子粒子群优化算法具有公式简洁、易于实现、参数调节少、所需种群规模较小、计算效率高、收敛速度快等优点。但在算法迭代末期,粒子位置受定权重下的个体最优解影响,导致粒子位置陷入局部最优解[26]。为解决这一问题,引入了平均最优位置mbest,其表达式如下:
(17)
式中:Pi为个体最优位置;n为粒子数。
由式(17)可知,平均最优位置mbest为当前所有个体最优位置的平均值。
引入平均最优位置mbest量子粒子群算法的粒子位置更新公式如下:
(18)
由式(18)可知,由于迭代末期种群恶化,局部吸引因子Lai中全局最优陷入个体最优,而引入平均最优位置mbest取代局部吸引因子Lai,通过平均值增加粒子间的消息交流,避免在历代迭代粒子中陷入局部最优,从而优化下代种群质量。
4.2 改进算法验证
为验证改进量子粒子群优化算法的可行性与有效性,笔者对比改进算法与粒子群优化算法在求解三种典型目标函数时的收敛速度、寻优性能等方面的能力。
目标函数F1为:
(19)
其中,自变量x的取值范围为[-100,100]。
目标函数F2为:

(20)
其中,自变量x的取值范围为[-32,32]。
目标函数F3为:
(21)
其中,自变量x的取值范围为[-600,600]。
函数F1为单峰函数,存在一个极值,其用于检验算法局部寻优能力;函数F2、F3为多峰函数,用于检验算法全局寻优能力。
F1、F2、F3进行仿真求解的最优适应度曲线如图5所示。

图5 适应度变化曲线
由图5可知:通过适应度变化曲线图可以看出:基于混沌序列与平均最优值的改进量子粒子群算法不管求解多峰还是单峰函数,改进算法在寻优能力与收敛精度上,均强于普通量子粒子群算法[27]。
5 姿态误差估计与姿态解算实验
姿态估计实验源数据来源于公开数据库。忽略机械结构振动和电机磁场对姿态测量的影响,数据采集于XC-M305型三轴MEMS陀螺仪。

扩展卡尔曼滤波中的Q、R值,采用基于混沌序列与平均最优值的改进量子粒子群算法进行参数寻优。其具体步骤如下:
1)参数初始化,并通过分段映射生成初始种群;
2)将陀螺仪数据输入扩展卡尔曼滤波器,同时将历代迭代中粒子位置作为Q、R,并计算测量数据的适应度值;
3)个体最优位置中适应度值最好的,作为全局最优值;
4)根据种群规模与个体最优位置,计算平均最优位置;
5)进入下次迭代,基于个体最优值、平均最优值与全局最优值,更新粒子位置;
6)计算新的粒子适应度值,更新个体最优值与全局最优值;
7)如果符合终止条件,终止寻优计算,输出最优值,即为卡尔曼滤波中的最佳Q、R。否则,继续执行步骤4)~步骤6),直到达到迭代的最大次数,输出所述卡尔曼滤波中的最佳Q、R数值。
笔者采用MATLAB软件实现上述参数寻优过程。算法参数设计如表1所示。

表1 IQPSO参数
姿态解算实验的适应度函数是经扩展卡尔曼滤波后得到的MSE值,解算实验初始转速值为三个仪器标定值。笔者设置结束条件为MSE小于或等于10-3。
参数优化结构记录如表2所示。

表2 IQPSO优化扩展卡尔曼参数
由表2可知:对于三组MEMS陀螺信号,经过基于混沌序列平均最优位置的改进量子粒子群算法参数寻优后,Q值偏小,R值较大,MSE小于设定值。因此,该优化算法能实现自动寻优,寻到全局最优参数。
5.1 IQPSO-EKF对比实验
为了测试IQPSO-EFK算法的有效性和精确性,笔者分别在转速为1.50°/s、-3.05°/s、6.04°/s下对陀螺仪测量值、扩展卡尔曼滤波、QPSO-EFK和IQPSO-EFK做了对比实验,实验结果如图6所示。

图6 +1.50°/s条件下对比图
由图6可知:在转速+1.50°/s条件下,扩展卡尔曼滤波的姿态估计误差为-0.30°~0.34°;QPSO-EKF的姿态角估计误差为-0.11°~0.14°;IQPSO-EKF的姿态角估计误差为-0.08°~0.08°。
-3.05°/s条件下对比图如图7所示。
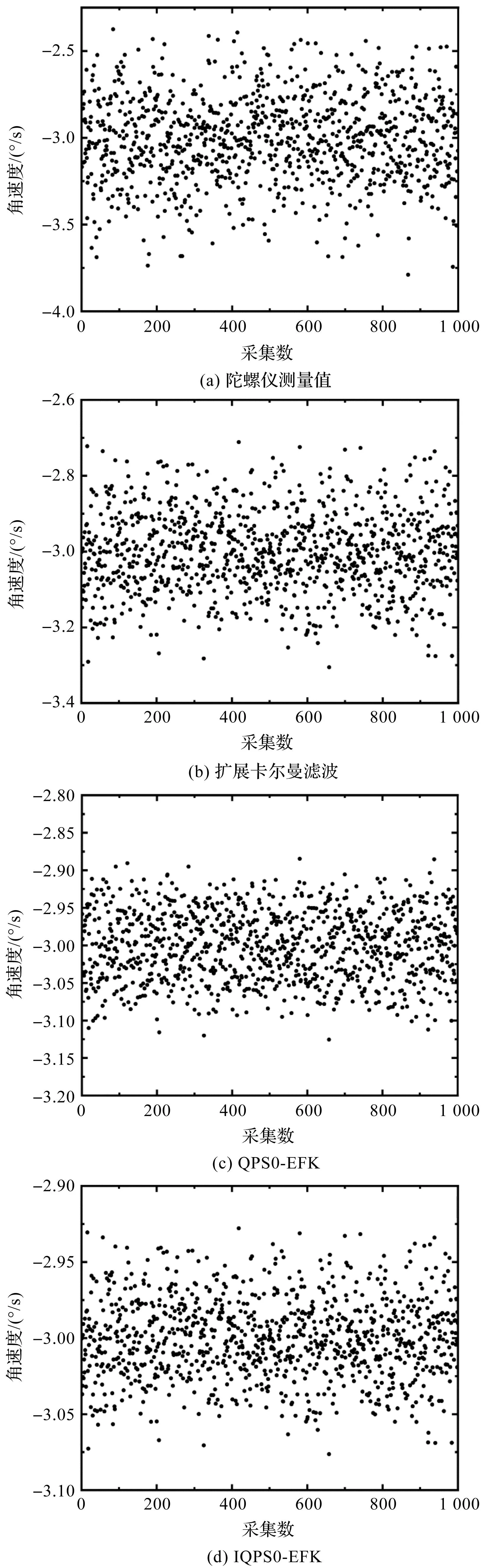
图7 -3.05°/s条件下对比图
由图7可知:在转速-3.05°/s条件下,扩展卡尔曼滤波的姿态估计误差为-0.32°~0.30°;QPSO-EKF的估计误差为-0.12°~0.11°;IQPSO-EKF的估计误差为-0.08°~0.08°。
+6.04°/s条件下对比图如图8所示。

图8 +6.04°/s条件下对比图
由图8可知:在转速+6.04°/s条件下,扩展卡尔曼滤波法的姿态角估计误差为-0.38°~0.34°;QPSO优化扩展卡尔曼滤波的姿态角估计误差为-0.11°~0.12°;改进QPSO优化扩展卡尔曼滤波的姿态角估计误差为-0.12°~0.10°。
为了验算基于IQPSO-EKF优化后的解算位置姿态误差,笔者分别对真实姿态、测量姿态、扩展卡尔曼优化姿态作了对比实验。
其姿态解算坐标对比如图9所示(其中,粗直线为设备真实解算位置,双点划线为陀螺仪测量数据的解算位置,点线为扩展卡尔曼滤波优化后的解算位置,点划线为基于IQPSO-EKF优化后的解算位置)。

图9 姿态解算坐标对比
由图9可以看出:对比真实姿态、MEMS传感器测量姿态和基于EFK方法解算的姿态,基于IQPSO-EKF方法解算姿态更接近真实值,从而达到了优化目的[30-31]。
5.2 MAE、MSE评价指标表
为更直观地对改进量子粒子群算法与其他优化算法姿态误差估计效果进行对比评估,笔者计算各优化算法在MEMS陀螺仪不同角速率下的MAE、MSE指标。
其具体计算结果如表3所示。

表3 评价指标表
由表3中可以看出:笔者采用基于混沌序列与平均最优值的改进量子粒子群算法优化扩展卡尔曼滤波方法,对MEMS陀螺姿态数据进行了误差估计,MAE、MSE值均下降了约86.7%、68.7%、28.2%。
由此可见,采用IQPSO-EFK方法能减小竖井掘进姿态测量误差。
6 结束语
笔者首先分析了竖井传感器设备现状,采用基于多传感器数据融合技术,配置多传感器姿态测量硬件,进行了姿态测量方法研究;然后,分析了竖井掘进设备姿态特征,利用多传感器数据信息,建立了描述竖井装备姿态特性的坐标系,分析了基于扩展卡尔曼滤波器进行多传感器数据融合方法的误差来源,针对扩展卡尔曼滤波算法的特点,采用量子粒子群优化算法进行了扩展卡尔曼滤波算法参数优化;同时依据算法特点,引入混沌序列与平均最优值改进方法,提出了一种基于分段映射与平均最优值的改进量子粒子群优化算法,并进行了实验验证;最后,进行了竖井掘进姿态测量与估计对比实验,将改进量子粒子群优化算法优化扩展卡尔曼滤波方法与其他方法对比,进行了姿态解算实验。
研究结果表明:
1)IQPSO-EFK不管求解多峰还是单峰函数,该改进算法在寻优能力与收敛精度上,均强于QPSO-EFK;
2)在三种不同的转速下,根据MAE、MSE评价指标,IQPSO-EFK对比原数据、EFK、QPSO-EFK,其值分别下降了约86.7%、68.7%、28.2%;
3)在姿态对比实验中,IQPSO-EFK方法更接近真实姿态,因此,其能减小竖井掘进姿态测量误差。
因为模型细节尚未完善,所以现阶段的具体实验很难进行实例验证。考虑竖井掘进机模型较为庞大,因此,笔者后续的研究方向为完善竖井掘进机的模型细节和具体安装细节。

