倒边盖挖逆作法基坑支护结构可靠性分析

陈威 王立 梅蕊 俞军 孙阳

摘 要：

為了解决采用标准Monte Carlo法计算复杂基坑工程上常见小概率失效，导致计算效率低的问题，以南京市湖南路地下商业街工程为工程背景，首先，将随机响应面法与基坑工程三维模型相结合，求解极限功能函数的响应面方程，并用标准Monte Carlo法计算失效概率和可靠指标，探讨采用倒边盖挖逆作法作为基坑支护结构施工方法的可行性；其次，基于该响应面方程，以土体的弹性模量为随机变量参数，采用马尔可夫链蒙特卡罗子集模拟法（MCMC子集模拟法）计算基坑支护结构的失效概率，并与标准Monte Carlo法结果进行对比分析。结果表明：当支护结构最大侧移控制指标为25 mm时，计算得到的可靠指标均大于4.6，即采用倒边盖挖逆作法施工过程中基坑是安全的；10万次和50万次标准Monte Carlo法计算得到的失效概率均为零，说明对于标准Monte Carlo法，在计算小概率失效问题时10万与50万的样本量是不足的；而MCMC子集模拟法用2.98万个样本计算出的结果与标准Monte Carlo法采用100万个样本计算的结果相对误差仅为1.7%，表明MCMC子集模拟法对于小概率失效问题求解的优势。所提算法在一定程度上提高了计算结构系统小概率失效问题的效率，对结构系统可靠性的相关研究具有一定参考价值。

关键词：

地下工程；基坑；可靠度；随机响应面法；Monte Carlo法；MCMC子集模拟法

中图分类号：

TU437

文献标识码：A

DOI： 10.7535/hbgykj.2024yx01005

Reliability analysis of supporting structure of foundation pit with inverted cover excavation and top-down construction method

CHEN Wei1， WANG Li1， MEI Rui2， YU Jun3， SUN Yang2

（1Power China of Huadong Engineering Copporation Limited， Hangzhou， Zhejiang 311122， China; 2College of Port， Coastal and Offshore Engineering， Hohai University， Nanjing， Jiangsu 210098， China; 3Zhejiang Police College， Hangzhou， Zhejiang 310053， China）

Abstract：

To solve the low computational efficiency of the standard Monte Carlo method to calculate the common small probability of failure problems in complex foundation pit projects， took the underground commercial street project on Hunan Road in Nanjing as the engineering background. Firstly， the stochastic response surface method was combined with the three-dimensional model of the foundation pit project， the response surface equation of the limit function was solved， and the probability of failure and the reliability index were calculated with the standard Monte Carlo method. Then， based on the response surface equation， the Markov chain Monte Carlo subset simulation method （MCMC subset simulation method） was used to calculate the failure probability of the foundation pit support structure with the elastic modulus of the soil as the random variable parameter， and the results were compared with those of the standard Monte Carlo method. The results show that when the maximum lateral displacement control index of the supporting structure is 25 mm， the calculated reliability index is greater than 4[DK（].[DK）]6， indicating that the pit is safe during the construction of inverted cover excavation; The failure probability of 100 000 and 500 000 times of the standard Monte Carlo method is zero， which indicates that for the standard Monte Carlo method， the sample sizes of 100 000 and 500 000 times are not enough to calculate the problem of small probability of failure. The relative error between the results calculated by MCMC subset simulation method with 29 800 samples and the result calculated by the standard Monte Carlo method with 1 000 000 samples is only 1[DK（].[DK）]7%， which shows the advantage of MCMC subset simulation method for the solution of small probability of failure problems. The proposed algorithm improves the efficiency of calculating the small probability failure problem of structural systems to a certain extent， which is of some reference value for the research related to the reliability of structural systems.

Keywords：

underground construction; foundation groove; reliability; stochastic response surface method; Monte Carlo method; MCMC subset simulation method

目前，国内外基坑开挖的主流方法有明挖顺作法、暗挖顺作法、盖挖顺作法以及盖挖逆作法[1-5]。相比其他方法，盖挖逆作法具有高安全、短工期、高质量等方面的优势，且对周围环境的影响也小，有着较好的社会价值和经济价值[6]。盖挖逆作法是先施作基坑的围护结构和覆盖板，然后在覆盖板的保护下进行基坑的支护与开挖的一种基坑开挖方法。由上往下一边开挖一边施作底板、边墙，覆盖板作为车站结构的顶板使用，然后恢复路面。

由于盖挖逆作法在施工过程中土体与地下结构相互作用关系复杂且施工步序特别、荷载组合变化众多，对施工中结构的力学响应一直是研究难点，对盖挖逆作法的研究越来越受到土木工程界的广泛关注[7]。

传统的变形分析方法是采用安全系数来表征支护结构的变形指标，这样的变形指标无法考虑到实际工程中存有的不确定性因素[8]，如土体材料参数、荷载组合形式、结构抗力大小等，安全系数难以对此进行准确的评估。引入结构可靠性分析方法可以解决上述问题。陈沛等[9]、盛建龙等[10]基于随机响应面法，以土（岩）体参数为随机变量分析了边坡稳定可靠度；廖瑛等[11] 采用响应面法计算了基坑支护结构抗倾覆稳定、坑底隆起稳定和抗滑移稳定可靠指标及失稳概率；曹净等[12-13]基于响应面法开展了土层抗剪强度指标c、φ间的互相关性对基坑支护结构稳定可靠性影响分析，并将其运用于支护结构优化设计中；张隆松等[14]基于概率密度加权法和Bootstrap方法提出了考虑岩土体参数统计不确定性的基坑变形可靠度高效蒙特卡罗（Monte Carlo）分析方法。

目前随机响应面法较少用于基坑支护结构的可靠度分析，本文采用随机响应面法结合基坑工程三维模型求得极限功能函数的响应面方程，并用标准Monte Carlo法计算失效概率和可靠指标。同时，采用高效的MCMC子集模拟法，用相对少的样本量计算可靠度，与标准Monte Carlo法结果进行对比分析，以期为深基坑支护结构的设计施工提供新的参考依据，从而使基坑工程的设计更为经济、安全，性能评估更为合理。

1 可靠度计算原理

1.1 标准Monte Carlo法

对于一般多维数问题及复杂积分域或隐式积分域问题，失效概率Pf可表示为失效域指示函数IF（x） 的数学期望形式。

Pf=…∫g（x）≤0fx（x1，x2，…，xn）dx1dx2…dxn=

…∫RnIF（x）fx（x1，x2，…，xn）dx1dx2…dxn=

E［IF（x）］，[JY]（1）

式中：IF（x）=1， x∈F0， xF为失效域的指示函数；Rn为n维变量空间；E［·］为数学期望算子。

以随机变量的联合概率密度函数fx（x）抽取N个样本点xj（j=1，2，…，N），落入失效域F内样本点个数Nf与总样本点个数N之比就是失效概率的估计值P^f，即：

P^f=1N∑Nj=1IF（xj）=NfN。（2）

1.2 随机响应面法

随机响应面法计算精度高、计算效率高，且其收敛性在数学意义上有严格保证，是用于大型复杂工程结构可靠度分析的一种有效方法。其原理如下。

把随机空间下的基本变量X映射到标准正态分布空间U中，即：

X=F－1Φ（U），（3）

式中：F－1·为X累计概率分布函数的反函数；Φ（·）為标准正态分布的累计概率分布函数。对于正态分布空间中的随机变量X，与标准正态分布空间中变量的映射关系如下。

X=μx+σxU，（4）

式中：μx和σx分别为X的均值和标准差；U为标准正态分布空间下的随机变量。输出的响应量Y如式（5）所示。

Y=a0+∑ni1=1ai1Γ1（Ui1）+

∑ni1=1∑i1i2=1ai1i2Γ2（Ui1，Ui2）+

∑ni1=1∑i1i2=1∑i2i3=1ai1i2i3Γ3（Ui1，Ui2，Ui3）+

∑ni1=1∑i1i2=1∑i2i3=1∑i3i4=1ai1i2i3i4Γ4（Ui1，Ui2，Ui3，Ui4）+L，[JY] （5）

式中：a0、ai1、ai1i2等为待定系数；U=（U1，U2，…，Un）为独立标准正态分布空间中的随机向量；n为标准正态随机变量的个数；Γn=（U1，U2，…，Un）为n阶Hermite多项式。

计算中，常用配点法计算上述随机多项式的待定系数。通常而言，以p+1阶Hermite多项式的根确定p阶Hermite随机多项式展开的配点，即输入随机变量的取值。可选择的配点总数为

Nc=（p+1）M。（6）

ISUKAPALLI等[15]建议，为有效平衡每个配点的影响，配点数目取为待定系数的2倍为宜。最后采用数学回归方法求解待定系数，这样计算结果的稳健性较好。

1.3 子集模拟方法

对于基坑工程上常见的小概率问题，标准Monte Carlo法计算效率极低，甚至是无法接受的。子集模拟法恰恰就是针对这种问题进行可靠性分析的一种可行性方法，基本思想是将合理的中间失效事件引入，把小失效概率表达为一系列较大的条件失效概率的乘积。

子集模拟法有2大典型代表：基于分支的子集模拟法和基于马尔可夫链蒙特卡罗的子集模拟法（MCMC子集模拟法）。MCMC子集模拟法可以迅速模拟出感兴趣区域的样本点，在子集模拟法可靠性分析中，MCMC子集模拟法用来模拟服从条件概率密度函数的条件样本点，并以此来估计条件失效概率。由此，本文采用MCMC子集模拟法对基坑工程小概率问题进行求解。

由功能函数g（x）定义的失效域F={x：g（x）≤0}，可以引入b1>b2>…>bm=0一系列临界值，引入的这些临界值可以构成具有嵌套关系的失效事件Fk={x：g（x）≤bk}（k=1，2，…，m），此时F1F2…Fm=F，且Fk=∩ki=1Fi，根据概率论中乘法定理的包含关系，可以得到式（7）。

Pf=P{F}=P{∩mi=1Fi}=

P{Fm∩m－1i=1Fi}·P{∩m－1i=1Fi}=

P{FmFm－1}·P{Fm-1∩m－2i=1Fi}·P{∩m－2i=1Fi}=

P{F1}·∏mi=2P{FiFi－1}。[JY]（7）

假设m=4，且P{FiFi－1}为0.1量级时，Pf可以达到10－4量级，采用子集模拟法求解时仅需4个计算样本即可达到该量级，而采用标准Monte Carlo法求解此量级的小概率问题所需的计算样本会非常大。所以相比于标准Monte Carlo法，计算小概率问题时子集模拟法的计算效率更高。

2 基坑工程实例

2.1 工程概况

湖南路地下商业街东西全长1 030 m，建筑面积约91 955 m2，东端衔接南京地铁1号线玄武门站（运营），西端衔接南京地铁5号线山西路站（在建），如图1所示。湖南路地下商业街工程分为A、B、C、D 4个区域，其中A区地下室位于山西路西流湾市民广场及湖南路西侧快车道下，为3层框架结构，如图2所示。A区采用倒边盖挖逆作法施工，倒边施工即分2期施工，施工步骤及对应工况见表1。土层划分详情见表2，A区基坑开挖面基本坐落于2-4层粉质黏土中。

2.2 基坑有限元模型

采用ABAQUS建立三维有限元模型，取A区108轴线处的一列桩柱再向两边各取1/2桩间距。基坑总开挖深度H为17.28 m，分别为覆土层开挖2.18 m，负1层开挖4.95 m，负2层开挖4.5 m，负3层开挖5.65 m。

为了便于计算模拟，将复杂土层进行加权平均处理为3层，分别为基坑上部土层，基坑下部土层，持力岩层。考虑到边界效应的影响，模型横向左右各取基坑開挖宽度的3倍，竖向取基坑开挖深度的5倍，最终地基计算尺寸取为167 m×80 m×9 m。三维模型支护结构和土层划分如图3和图4所示。

结构采用均质混凝土进行模拟，通过等效刚度法换算得到弹性模量来考虑钢筋对结构刚度的影响。为了减少模型网格数量以降低计算时间，将圆截面的钢管混凝土柱与钻孔灌注桩刚度等效为矩形截面。土层材料参数见表3、表4。

三维有限元计算单元总数88 806个，其中土体单元为C3D8R实体单元，共58 656个；岩石单元为C3D8R实体单元，共28 704个。各层楼板和临时挡土墙为S4R壳单元，共734个；地下连续墙为实体单元，共522个；中间桩柱为C3D8R实体单元，共60个；临时混凝土支撑以及各层楼板主次梁为B31梁单元，共130个。

2.3 连续墙施工过程水平位移

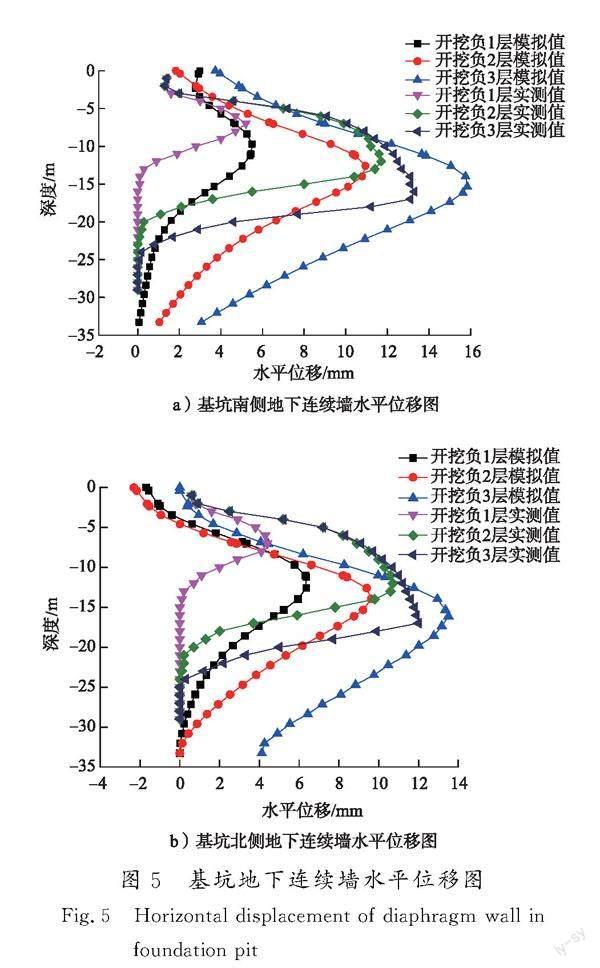
因第三方监测数据有限，本节仅对比水平位移变化较大的施工步下的实测值与模拟值，具体对比情况如图5所示。图中水平位移正值表示位移指向基坑，负值表示位移背离基坑。

从图5可以看出，数值模拟结果与现场实测结果较为接近，水平位移曲线形式与出现最大水平位移的墙体位置相近，具体数值见表5和表6。从数据上看，除了基坑北侧地下连续墙开挖负1层施工步的结果误差较大外，其余水平位移最大值模拟结果的相对误差均在20%以内，模拟结果较好。造成北侧地下连续墙开挖负1层水平位移最大值偏大的原因可能是本次模拟无法考虑到实际施工过程中土体开挖的“时空效应”，一次性开挖量过大，同时土层参数设置与实际情况存在一定误差。

3 支护结构可靠度分析

3.1 目标可靠度指标

国内外许多专家学者对目标可靠度指标的合理选取进行了相关研究，但由于研究尚不充分，在岩土工程领域目标可靠度指标尚未有统一标准。中国《建筑结构可靠度设计统一标准》（GB 50068—2001）中对建筑结构规定的目标可靠度指标如表7所示。由于基坑支护结构不同于建筑物结构，因此不能直接利用《建筑结构可靠度设计统一标准》所规定的目标可靠度指标，而是参考文献[16]—[17]进行取值，见表8和表9。本文对基坑支护结构的目标可靠度指标β取值为3.0，相应的失效概率Pr为0.1%。

3.2 可靠度计算

以南侧地下连续墙最大侧向位移作为可靠度分析的功能函数，以土体参数中的弹性模量为功能函数的随机变量进行结构可靠性分析。极限功能函数为

Z=g（E1，E2，E3）=fmax－f=0，（8）

式中：fmax为地下连续墙水平位移控制值，根据规范及工程设计要求选择其中较小值，最终取值为25 mm；f为地下连续墙施工过程中最大水平位移计算值；E1、E2、E3为基本变量，即土层、岩层的弹性模量。

土层与岩层弹性模量将其视为服从正态分布，且相互独立，弹性模量的取值即为平均值μ，变异系数δ取值为0.1。采用随机响应面法来建立极限功能函数的响应面方程。为了保证计算精度以及控制计算量，将三阶Hermite多项式函数展开。展开如式（9）所示：

Y=（a0）（1）+（a1）（U1）+（a2）（U2）+（a3）（U3）+（a11）（U12－1）+（a22）（U22－1）+

（a33）（U32－1）+（a111）（U13－3U1）+

（a222）（U23－3U2）+（a333）（U33－3U3）+

（a12）（U1U2）+（a13）（U1U3）+（a23）（U2U3）+

（a122）（U1U22－U1）+（a133）（U1U32－U1）+

（a211）（U2U12－U2）+（a233）（U2U32－U2）+

（a311）（U3U12－U3）+（a322）（U3U22－U3）+

（a123）（U1U2U3）。[JY]（9）

基本变量通过正态分布与标准正态分布的映射关系见式（4），将基本变量E映射到标准正态空间中。然后通过配点法选取40个配点，这些配点也需要映射到标准正态空间中。将这40个配点代入到ABAQUS三维模型中进行运算得到响应量f。将所得的配点与响应量代入式（9），得到关于多项式待定系数的方程组，经过计算，响应面方程待定系数如表10所示。确定响应面方程后，即可进行可靠度求解。由于本文地下连续墙失效属于小概率事件，故采用基于马尔可夫链蒙特卡罗的子集模拟法（SS/MCMC）对工程小概率问题进行求解。同时运用标准Monte Carlo法进行求解，将100万次的计算结果作为精确值。

在子集模拟的实际应用中，假设失效事件可以定义为系统的某一临界响应变量Y值低于特定的阈值y，即F={Yy2>…>ym=y>0为一个递减的中间阈值序列。中间阈值的选取是适应性的，以条件失效概率估计总是等于某一个定值p0。MCMC子集模拟法的流程如图6所示。

图6中，xk0：k=1，2，…，N为从原始密度函数中抽取的N个样本点，这些样本点对应于第0条件水平；Y（xki）：k=1，2，…，N计算得到相应的响应变量；yi为当中第1个中间阈，取值为降序排列的Y（xk0）：k=1，2，…，N中的第（1－p0）位。

3.3 计算结果分析

标准Monte Carlo法和MCMC子集模拟法抽样计算结果如表11所示。本工程中基坑的失效概率小于10-5，是典型的小概率失效問题。采用标准Monte Carlo法抽样10万次和50万次计算得到的失效概率均为0，说明对于基坑工程问题，标准Monte Carlo法所需的计算样本较大，计算效率较低。而MCMC子集模拟法仅用了2.98万个样本点，就算得了结果，且与标准Monte Carlo法计算的相对误差仅为1.7%，满足工程精度要求。显然子集模拟法在复杂工程问题上的计算效率和计算精确度较高，充分体现了子集模拟对于小概率问题求解的优势。通过计算得到的可靠指标为4.672 6明显大于目标可靠指标3.0，表明基坑预期的性能水平高于平均水平，在好与极好之间，采用倒边盖挖逆作法施工是安全可靠的。

4 结 语

结合南京市湖南路地下商业街工程，基于随机响应面法，对采用标准Monte Carlo法和MCMC子集模拟法计算得到的失效概率和可靠度指标进行对比分析，得出以下主要结论。

1）倒边盖挖逆作法施工时，当支护结构最大侧移控制指标为25 mm时，计算得到的基坑可靠度指标均大于4.6，失效概率小于10-5，基坑安全性能很高。

2）对于复杂工程中的小概率失效问题，采用MCMC子集模拟法计算可靠度较标准Monte Carlo法所需样本数量少，计算效率高且得到的可靠度计算结果十分精确。

3）标准Monte Carlo法计算小概率失效问题的可靠度，必须采用大量的抽样样本点才能得到收敛的失效概率估计值。它的解更适合在理论研究中作为精确解来检验其他新方法的正确性。

未来可对提出的计算方法进行改进，给出新的计算方法或者更加合理的样本数，进而提高计算效率；进一步分析结构系统可靠性的灵敏度以及优化问题；将提出的计算方法应用于动力学问题，分析复杂动态载荷作用下的结构系统可靠性。

参考文献/References：

[1]

李阳，袁晏仁，高东波，等.复合地层明-暗挖法结合地铁车站暗挖进洞施工技术[J].现代隧道技术，2018，55（sup2）：82-88.

LI Yang，YUAN Yanren，GAO Dongbo，et al.Construction technology of open cutting with undermining metro station in mixed ground[J].Modern Tunnelling Technology，2018，55（sup2）：82-88.

[2] 于素慧，耿永常.明挖法地下工程近接既有建筑施工影響分析[J].地下空间与工程学报，2019，15（sup1）：266-277.

YU Suhui，GENG Yongchang.Influence analysis on underground approaching adjacent buildings construction with cut and cover method[J].Chinese Journal of Underground Space and Engineering，2019，15（sup1）：266-277.

[3] 徐鑫磊.地铁隧道浅埋暗挖法安全风险管理研究[D].青岛：山东科技大学，2019.

XU Xinlei.Study on Safety Risk Management of Shallow Excavation in Subway Tunnel[D].Qingdao：Shandong University of Science and Technology，2019.

[4] 徐曼，陈玮，李金强，等.地铁车站盖挖顺作法路面体系荷载分析及方案设计[J].施工技术，2017，46（13）：128-131.

XU Man，CHEN Wei，LI Jinqiang，et al.Analysis and construction design of cover-excavation pavement load system in subway station[J].Construction Technology，2017，46（13）：128-131.

[5] 陶连金，代希彤，黄美群，等.盖挖逆作法与明挖顺作法施工变形控制对比[J].辽宁工程技术大学学报（自然科学版），2020，39（2）：136-144.

TAO Lianjin，DAI Xitong，HUANG Meiqun，et al.Contrast between cover and cut-top down method and cut-cover method for deformation control[J].Journal of Liaoning Technical University（Natural Science），2020，39（2）：136-144.

[6] 丁志刚，邹强，包文成，等.盖挖逆作法施工对基坑周边变形影响研究[J].人民长江，2021，52（sup1）：159-163.

DING Zhiqiang，ZOU Qiang，BAO Wencheng，et al.Research on the influence of cover-excavation top-down construction method on the surrounding deformation of foundation pit[J].Yangtze River，2021，52（sup1）：159-163.

[7] 何云猋，李洪亮，何彦荣，等.盖挖逆作地铁车站深基坑开挖变形实测分析[J].建筑结构，2021，51（sup1）：1940-1944.

HE Yunbiao，LI Hongliang，HE Yanrong，et al.Analysis of measured deformation during the excavation of the deep foundation pit in a subway station using the cut-and-cover top-down method[J].Building Structure，2021，51（sup1）：1940-1944.

[8] 蒋水华，刘贤，黄劲松，等.考虑水力模型参数空间变异性土石坝边坡可靠度分析[J].应用基础与工程科学学报，2021，29（4）：939-951.

JIANG Shuihua，LIU Xian，HUANG Jinsong，et al.Reliability analysis of slope stability of embankment dams considering spatial variability of hydraulic model parameters[J].Journal of Basic Science and Engineering，2021，29（4）：939-951.

[9] 陈沛，苗作华，董舒，等.基于随机响应面法的风化岩质边坡稳定可靠度分析[J].矿业研究与开发，2018，38（11）：51-56.

CHEN Pei，MIAO Zuohua，DONG Shu，et al.Stability and reliability analysis of weathered roch slope based on random response surface method [J].Mining research and development，2018，38（11）：51-56.

[10]盛建龙，翟明洋.基于随机响应面法的金鸡岭岩质边坡可靠度分析及抽样方法对比[J].黄金科学技术，2018，26（3）：297-304.

SHENG Jianlong，ZHAI Mingyang.Reliability analysis and sampling method comparison of jinjiling rock slope based on stochastic response surface method[J].Gold Science and Technology，2018，26（3）：297-304.

[11]廖瑛，樊伯旺.基于响应面法的基坑支护结构稳定可靠度分析[J].盐城工学院学报（自然科学版），2019，32（2）：60-65.

LIAO Ying，FAN Bowang.Analysis of stable reliability of foundation pit supporting structure based on response surface method[J].Journal of Yancheng Institute of Technology （Natural Science Edition），2019，32（2）：60-65.

[12]曹净，刘甜，桂跃.c、φ互相关性对基坑支护可靠度的影响[J].控制工程，2018，25（1）：30-36.

CAO Jing，LIU Tian，GUI Yue.Influence of mutual correlations of c and φ on the reliability of the foundation pit supporting structure [J].Control Engineering of China，2018，25（1）：30-36.

[13]曹净，刘甜，桂跃.基于响应面法的基坑支护可靠度优化[J].控制工程，2017，24（9）：1811-1817.

CAO Jing，LIU Tian，GUI Yue.Foundation pit supporting reliability optimization based on the response surface method[J].Control Engineering of China，2017，24（9）：1811-1817.

[14]張隆松，李典庆，曹子君，等.考虑统计不确定性的基坑变形可靠度高效蒙特卡洛分析方法[J].武汉大学学报（工学版），2019，52（3）：207-215.

ZHANG Longsong，LI Dianqing，CAO Zijun，et al.Efficient reliability analysis of excavation deformation considering statistical uncertainty using Monte Carlo simulation[J].Enigineering Journal of Wuhan University，2019，52（3）：207-215.

[15]ISUKAPALLI S S，ROY A，G GEORGOPOULOS P G.Stochastic response surface methods （srsms） for uncertainty propagation：Application to environmental and biological systems[J].Risk Analysis，1998，18（3）：351-363.

[16]孙勇.单排抗滑桩随机有限杆单元法计算的分析与研究[J].中国地质灾害与防治学报，2009，20（2）：123-128.

SUN Yong.Analysis and research on the calculation of stochastic finite bar element method of the single-row anti-slide pile[J].The Chinese Journal of Geological Hazard and Control，2009，20（2）：123-128.

[17]CAO Zijun，WANG Yu，LI Dianqing.Probabilistic Approaches for Geotechnical Site Characterization and Slope Stability Analysis[M].Berlin：Springer，2017.

收稿日期：2023-05-06;修回日期：2023-12-27；责任编辑：王淑霞

基金项目：国家自然科学基金（41672257）；浙江省交通运输厅科技计划项目（2020014）

第一作者简介：

陈威（1984—），男，江苏高邮人，高级工程师，主要从事结构振动分析方面的研究。

通信作者：

孙阳副教授。E-mail：20140023@hhu.edu.cn

陈威，王立，梅蕊，等.

倒边盖挖逆作法基坑支护结构可靠性分析

［J］.河北工业科技，2024，41（1）：36-43.

CHEN Wei，WANG Li，MEI Rui，et al.

Reliability analysis of supporting structure of foundation pit with inverted cover excavation and top-down construction method

［J］. Hebei Journal of Industrial Science and Technology，2024，41（1）：36-43.