内衬GFRP防护复合管壁原缺陷坑处应力重分布规律分析
卢召红,彭郑飞,王佳美
(东北石油大学 土木建筑工程学院,黑龙江 大庆 163318)
长期服役的输油管道在内部运输介质或外界环境等因素的综合影响下,管道内壁极易发生腐蚀,形成内腐蚀缺陷坑[1],从而影响到了管道运输的安全性。薄壁内衬复合管修复技术是一种伴随非开挖基础的一种新型管道技术。采用少量开挖或不开挖的方式,将玻璃钢材料摊涂到破损管道内部,使玻璃钢内衬管与原有腐蚀部分管道的管壁贴合在一起,形成复合管道结构,提高管道的安全性[2-3]。研究原管道内侧腐蚀缺陷坑处的应力状态是研究管道力学性能和修复效果的一种重要途径,研究腐蚀缺陷坑处的应力分布问题对于内衬修复后的复合管修复效果具有重要意义[4]。
目前,国内外学者对石油管道腐蚀后的修复问题已有一些卓有成效的研究成果,陈严飞等[5]研究了组合荷载作用下腐蚀缺陷管道的受力状况。邓磊等[6]解析了在双均值逼近屈服准则情况下的含腐蚀缺陷管道的应力状况。黄坤等[7]将单腐蚀坑简化成球形缺陷,基于ANSYS软件建立有限元模型对管内应力分布进行分析。李晓丽等[8]利用有限元分析软件模拟埋地管道在复杂载荷作用下的应力应变,并对内压埋深等因素的影响进行了分析。崔进起等[9]采用ABAQUS软件对含腐蚀缺陷的长输油管三维建模,并分析了其剩余强度。卢召红等[10]通过对不同腐蚀程度的管道钢进行拉伸试验,研究得到了腐蚀坑的最大深厚比是影响管钢腐蚀坑处的应力集中系数的主要因素;将内衬层为不锈钢的复合管进行切向和法向拉伸破坏试验,基于结果,建立了带腐蚀缺陷管钢修复后的有限元分析模型,进行数值分析后的结果与试验结果相比较得出,双线性界面内聚力模型在有限元分析中能够准确模拟薄壁内衬复合管材层间力学性能。杨理践等[11]基于形状改变能强度准则(Mises强度准则[12]),推导了管道极限承载力的计算公式,并采用有限元软件进行了分析,验证了公式的正确性。
前人对管道内部腐蚀的研究主要集中于缺陷参数对腐蚀管道压力的影响规律[13-14]以及对腐蚀管道剩余强度[15-16]的探究,对腐蚀管道修复前后腐蚀坑处应力分布状态的研究较少。因此,为了深入地研究内压作用下不同深厚比,薄壁内衬修复前后原管钢内腐蚀缺陷处的应力分布规律。本文基于弹塑性力学中的平衡微分方程,建立原管钢内腐蚀缺陷处的应力计算模型,并利用有限元软件建立薄壁内衬修复前后的腐蚀管道模型,对其腐蚀坑处应力状态展开分析,为管道的安全评估和修复补强提供参考。
1 物理模型
管壁原始状态为轴对称等厚度圆筒形式,在内压作用下,可由拉梅方程[17]确定沿管壁厚度方向的应力值,管道为长距离输送管道,忽略管道轴线方向的应力应变,为计算时简化为平面应力问题提供依据。当管壁出现缺陷,应力在缺陷位置具有集中现象,压力作用下腐蚀缺陷处的应力对薄壁内衬复合管层间作用力具有较大的影响,也是影响修复效果和修复后脱层剥离的主要因素。
图1为内腐蚀缺陷管道壁的截面简图。图中θ为单腐蚀坑的缺陷宽度,即缺陷沿管壁周向的尺寸;AD为管壁完整无缺陷处的壁厚bm,b为缺陷处的剩余厚度,BC为坑底处剩余最小厚度bm,min。
2 数学模型
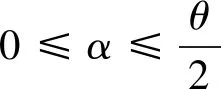
在管壁内缺陷处取一点E(r,α),分别沿径向取微分段dr,沿管壁的周向取微分段dα,如图2所示,红线部分表示微元体受力变形后。建立微分方程如式(1)所示。

图2 E点数学模型
(1)
由广义胡克定律和变形协调方程[18]得:
(2)
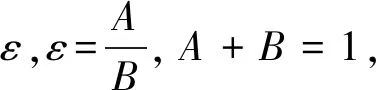
(3)
当A=0时,ε=0,管壁完整无缺陷,式(3)即为无缺陷管壁径向压力作用下应力表达式。
当B趋近于0,管壁缺陷处趋向于穿孔时,将式(3)进行一次积分并简化得式(4):
(4)
根据实际情况得知腐蚀缺陷宽度α远小于管道半径r,故引入系数η=α/r,可解得式(5):
(5)

根据边界条件即可确定式中常数项C1,C2和C3。
3 有限元模型
3.1 尺寸及材料基本属性
本次分析的管道材质为API5LX52 N管线钢,管道外直径D=324 mm,壁厚h=10 mm,为各向同性材料,材料本构关系为理想的弹塑性模型,弹性模量为2.2×1011Pa,密度为7.85×103kg/m3,泊松比为0.28,屈服强度为360 MPa。对内腐蚀缺陷管道,为了有效提高管道的安全性,采用滩涂式内衬GFRP进行修复补强。其材料属性:弹性模量为7.25×1010Pa,密度为725 kg/m3,泊松比为0.3。
3.2 单元网格划分
根据管道内壁的腐蚀缺陷体积形状,将对实际不规则的体积缺陷进行简化处理,采用ABAQUS CAE软件建立三维的单腐蚀缺陷管道模型。单腐蚀有效宽度ω=20 mm,深厚比h/bm分为0.0、0.1、0.3、0.5、0.8五种情况。单元类型采用六面体实体单元(C3D8),网格尺寸为0.001 m×0.001 m,径向网格划分10份,环向划分为478份。
对于玻璃钢内衬的复合管,玻璃钢采用滩涂式填满缺陷坑的方式,内衬层与外管壁之间采用高性能结构胶,层间采用粘接行为建立界面作用分析模型[19],在分析复合管壁径向压力作用下的内力时,假定复合管层间结合紧密无间隙;薄壁内衬层沿壁厚方向应力分布均匀;粘合层为粘接材料固化层,忽略其径向的伸缩。网格划分及边界条件同原管道所述。模型如图3。
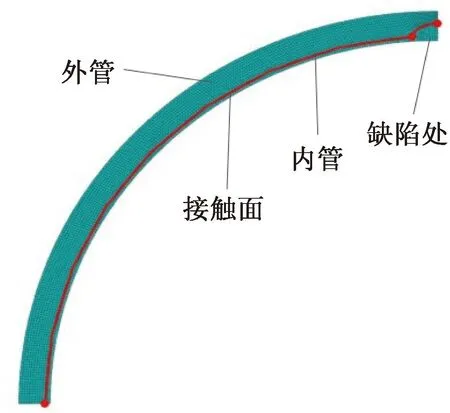
图3 有限元模型
3.3 荷载及边界条件
实际工程管内压一般在1~10 MPa不等,考虑数量级相同,为了方便计算,以管内施加P1=1.0 MPa静压力为例,压力方向沿径向作用,即垂直于管内表面。由于加载和模型的对称性,截取1/4模型进行分析,在对称面上固定X,Z方向上的位移与转角。模型没有旋转并沿轴向没有运动,所以对结构Z方向上的转角与位移进行约束。
4 计算结果及分析
4.1 数学模型与有限元模型计算结果对比分析
针对上述数学模型,对带有内腐蚀缺陷的管道,利用上述式(5),可计算出剩余厚度最小处,管壁沿壁厚方向的应力值,沿壁厚方向,随着半径的增大,选取各位置对应的周向应力和径向应力,并将计算结果与有限元分析结果对比得出图4。图4中黑线红线分别表示深厚比h/bm=0.1时管壁缺陷处应力的理论计算值和有限元分析值,从图4中可以看出,对于此时的周向应力和径向应力,有限元分析模型计算结果与数学模型理论计算结果基本吻合,可为进一步的分析提供依据。
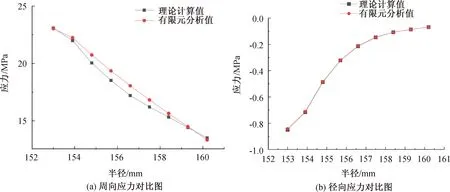
图4 理论计算值与有限元分析值对比图
4.2 修复前后复合管壁缺陷处应力状态分析
在管内压力的作用下,考虑腐蚀坑的深厚比h/bm的影响,参考数据,对比修复前后管壁径向应力σr,周向应力σα,和Mises应力σm的变化,对结果进行分析。
图5—图7为五种不同深厚比腐蚀缺陷处的应力分布状态,其中正值为拉应力,负值为压应力。如图5(a)所示,无缺陷完整管道,径向应力作用下,径向应力σr表现为压应力状态并沿壁厚由内到外逐渐减小。图5(b)—(e)为管道内腐蚀缺陷部位径向应力分布云图,由于出现局部缺陷,径向应力在缺陷处发生了重分布,腐蚀坑内出现了拉应力,且随着h/bm的增大而增大,但是最大拉应力不在腐蚀坑底而是出现在距坑底有一段距离的区域;在腐蚀坑边缘,压应力随着h/bm的增大而增大。由图5可见,腐蚀坑处的深厚比越大,其应力重分布的程度越明显,管道内壁缺陷处的最大径向应力值随着腐蚀坑深厚比的增大而迅速增大。
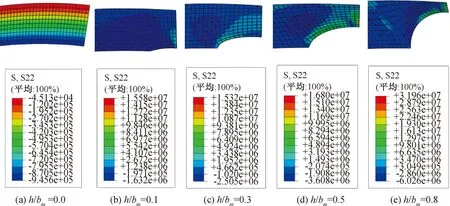
图5 管道径向应力 σr
根据图5,深厚比从0.1至0.8逐渐增大时,1.0 MPa内压下的管壁最大径向应力值分别为1.712、2.505、3.608、6.030 MPa。在管壁的最内侧,应力状态为压应力,应力值由内侧至外层逐渐减小。深厚比0.8时对应最大压应力为6.030 MPa,其值远小于钢材的材料屈服强度360 MPa;在腐蚀坑剩余厚度最薄的部位,管壁径向应力发生了重分布,由受压变成受拉状态,并随着深厚比的增大拉应力逐渐增大;当深厚比为0.8时,最大拉应力出现在坑底附近,其值为31.960 MPa,但仍远小于管钢屈服强度360 MPa。
如图6所示,当管道内侧出现腐蚀缺陷后,坑底周向应力发生了重分布,外侧的周向拉应力逐渐变小并随着腐蚀坑深厚比的增加逐渐变为压应力,深厚比0.8时对应最大压应力为165.900 MPa,内侧的拉应力逐渐增大,深厚比0.8时对应最大拉应力为269.600 MPa,其值已远大于管道完整时的周向最大应力15.660 MPa。
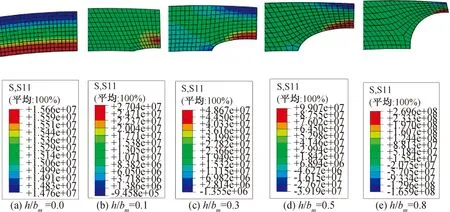
图6 管道周向应力 σα
如图7所示,在内压作用下,对于完整管壁即h/bm=0.0情况下,Mises应力在管壁内侧最大,其值为14.750 MPa,小于管壁的周向应力15.660 MPa,对于完整管道,其Mises应力略小于周向应力。随着腐蚀坑深厚比的增加逐渐,管壁内侧从只有拉应力(红色区域)慢慢出现了压应力(蓝色区域),管道外侧也从只有压应力(蓝色区域)出现了拉应力(红色区域),腐蚀坑处的Mises应力明显发生了应力重分布。
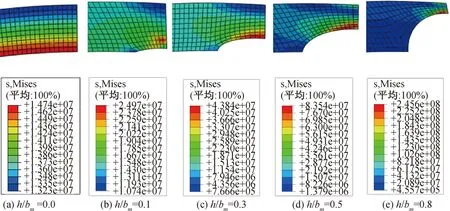
图7 管道Mises应力
经玻璃钢修复后,不同深厚比下修复前后应力云图均有明显改变,选取深厚比h/bm=0.5时进行分析,缺陷处各项应力图如图8。表1是四种不同深厚比缺陷处的应力最大值统计。
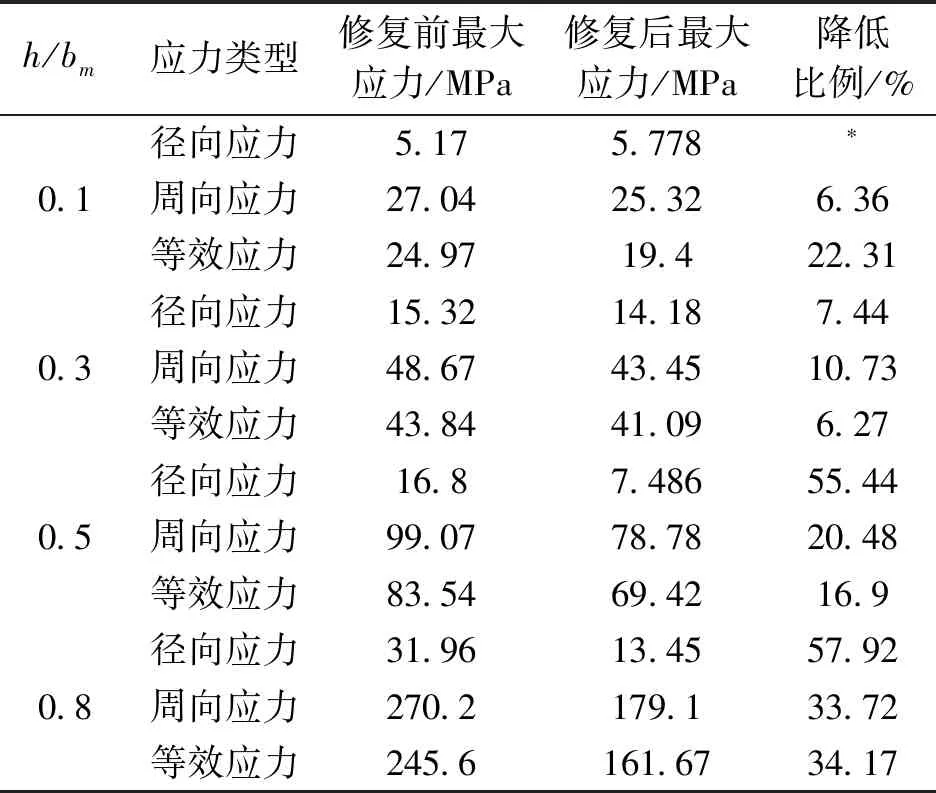
表1 修复前后缺陷处最大应力对比
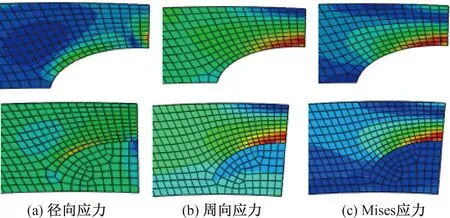
图8 h/bm=0.5时管壁修复前后应力云图
结合图8和表1,深厚比为0.5的带缺陷管壁,经玻璃钢修复后,径向应力最大值由16.801 MPa下降到了7.490 MPa,周向应力最大值从99.070 MPa下降到了78.780 MPa,Mises应力从83.540 MPa下降到了69.420 MPa。对照图8,缺陷部位的径向应力σr、周向应力σα和Mises应力σm均发生了变化。由表1可见,缺陷坑处应力发生了重分布,修复前后,径向应力值相对于周向和等效应力均偏小,虽然降低幅度较大,但周向应力仍起到了主控作用。
由表1可知,不同深厚比的腐蚀坑在修复前,腐蚀缺陷处的最大应力为周向应力,其值与Mises应力接近,因此带有腐蚀缺陷管道的失效判断可依据周向应力进行。经玻璃钢内衬修复后,腐蚀缺陷处的应力状态发生了重分布,原管壁腐蚀坑部位的周向应力和Mises应力均有较大幅度的减小,修复具有明显的补强效果;腐蚀缺陷处的应力最大值依旧是周向应力σα,周向应力σα是腐蚀缺陷处截面破坏的控制应力。
5 结论
1)利用拉梅公式建立了带球形内腐蚀缺陷管道应力状态分析模型,并选取腐蚀缺陷深厚比为0.1时,对缺陷处的应力进行计算分析。将理论计算结果与有限元分析结果对比,二者结果基本吻合。
2)腐蚀缺陷的深厚比对管壁上的应力状态有着重要的影响,在实际工程中进行安全评估和管线修复时应慎重考虑其影响。
3)内压作用下含有内腐蚀缺陷的管道,经过薄壁内衬修复后,原管壁缺陷处的周向应力均起着控制作用,随着缺陷深厚比的增大,该现象愈加明显。对于深厚比较大的缺陷管道,应将原管壁缺陷处的最大周向应力作为承载力设计计算的主要依据。

