Properties of collective flow and pion production in intermediate‑energy heavy‑ion collisions with a relativistic quantum molecular dynamics model

Si‑Na Wei · Zhao‑Qing Feng

Abstract The relativistic mean-field approach was implemented in the Lanzhou quantum molecular dynamics transport model (LQMD.RMF).Using the LQMD.RMF, the properties of collective flow and pion production were investigated systematically for nuclear reactions with various isospin asymmetries.The directed and elliptic flows of the LQMD.RMF are able to describe the experimental data of STAR Collaboration.The directed flow difference between free neutrons and protons was associated with the stiffness of the symmetry energy, that is, a softer symmetry energy led to a larger flow difference.For various collision energies, the ratio between the π− and π+ yields increased with a decrease in the slope parameter of the symmetry energy.When the collision energy was 270 MeV/nucleon, the single ratio of the pion transverse momentum spectra also increased with decreasing slope parameter of the symmetry energy in both nearly symmetric and neutron-rich systems.However, it is difficult to constrain the stiffness of the symmetry energy with the double ratio because of the lack of threshold energy correction on the pion production.

Keywords Heavy-ion collision · Collective flow · Pion production · Symmetry energy · Relativistic mean field

1 Introduction

The equation of state (EOS) of nuclear matter, which originates from the interactions between nuclear matter, plays an important role in nuclear physics and astrophysics.Heavyion collisions, the properties of nuclei, and neutron stars(NSs) have been widely studied to extract the nuclear EOS.Because nuclear many-body problems are highly nonlinear and the EOS is not a directly observable quantity in experiments, there are still some uncertainties in the EOS despite great efforts [1–6].For instance, the EOS extracted from the GW170817 event has uncertainties at high nuclear densities[2].Although the EOS can be extracted from the properties of NSs, the internal composition of NSs is still poorly understood.The core of an NS may contain exotic materials such as hyperons, kaons, pions, and deconfined quark matter [7–12].Heavy-ion collisions in terrestrial laboratories provide a unique opportunity to study both the EOS and exotic materials.

Collective flows of heavy-ion collisions were proposed in the 1970 s and first detected in experiments at Bevalac [13–16].Because collective flows are associated with nucleon–nucleon interactions, nucleon-nucleon scattering,etc., collective flows have been used to extract the nuclear EOS [1].Collective flows are also helpful for understanding the phase transition between hadronic and quark matter.Generally, when a phase transition between hadronic and quark matter occurs, the collective flows of heavy-ion collisions indicate a soft EOS [17–21].In addition, the ratios of the isospin particles in heavy-ion collisions, such asπ−∕π+,K0∕K+, and Σ−∕Σ+, are thought to be sensitive to the stiffness of the EOS [22–28].The production of pions and kaons has been experimentally measured in197Au+197Au collisions.TheK+production predicted by various transport models favors a soft EOS of isospin-symmetric nuclear matter at high baryon densities [29–33].Theπ−∕π+ratio predicted by various transport models is still model-dependent [34–37].Based on the FOPI data for theπ−∕π+ratio [38], some results favor a stiffsymmetry energy (isospin asymmetric part of the EOS) [34,35], whereas others imply a soft symmetry energy [36,37].Recently, by analyzing the ratios of charged pions in132Sn+124Sn ,112Sn+124Sn , and108Sn+112Sn collisions[39], a slope of the symmetry energy ranging from 42 to 117 MeV was suggested [40, 41].The collective flows and ratios of charged pions are still worth studying to find the sources of the difference in various transport models and to extract information about the EOS from heavy-ion collisions.

Quantum molecular dynamics (QMD) is a popular transport model that has been developed into many versions and used to successfully describe the properties of nuclear matter, nuclei, mesons, and hyperons [33, 34,42–55].In high-energy heavy-ion collisions, the relativistic effects should be considered in QMD because they become significant.The RQMD approach has been proposed for this purpose [42, 43].Recently, relativistic mean-field theory (RMF) was implemented in RQMD(RQMD.RMF) [44–46].The RQMD.RMF has been successfully applied to investigate the collective flows of hadrons [44–46].In this study, we implemented RMF theory with isovector-vector and isovector-scalar fields in the Lanzhou quantum molecular dynamics model (LQMD.RMF).The channels for the generation and decay of resonances ( Δ(1232), N*(1440), N*(1535), etc.), hyperons,and mesons were included in the previous LQMD model[33, 34, 47–50].Using the LQMD.RMF, we explored the relationship between the symmetry energy and the properties of the collective flow and pion production.

The remainder of this paper is organized as follows.In Sect.2, we briefly introduce the formulas and approaches used in this study.The formulas include RMF theory, the dispersion relation, and the production of pions.The results and discussion are presented in Sect.3.Finally, a summary is presented in Sect.4.

2 Formalism

2.1 Relativistic mean field approach

The RMF interaction is achieved by exchanging mesons.Scalar and vector mesons provide medium-range attraction and short-range repulsion between nucleons, respectively[56].The nonlinear self-interaction of theσmeson is introduced to reduce the incompressibility to a reasonable domain[57].To investigate the properties of symmetry energy, we also consider the isovector-vectorρ[58] and isovector-scalarδmesons [59].The Lagrangian density is expressed as [59,60]

whereMN=938 MeV is the nucleon mass in free space,giwithi=σ,ω,ρ,δis the coupling constant between nucleons,miwithi=σ,ω,ρ,δdenotes the meson mass,g2andg3are the coupling constants for the nonlinear self-interaction of theσmeson, andFμν=∂μων−∂νωμand Bμν=∂μbν−∂νbμare the strength tensors of theωandρmesons, respectively.The equations of motion for the nucleon and meson are obtained from the Euler–Lagrange equations and are written as:

whereρandρSare the baryon and scalar densities, respectively,ρ3=ρp−ρnis the difference between the proton and neutron densities, andρS3=ρSp−ρSnis the difference between the proton and neutron scalar densities.

In the RMF approximation, the energy density is given by

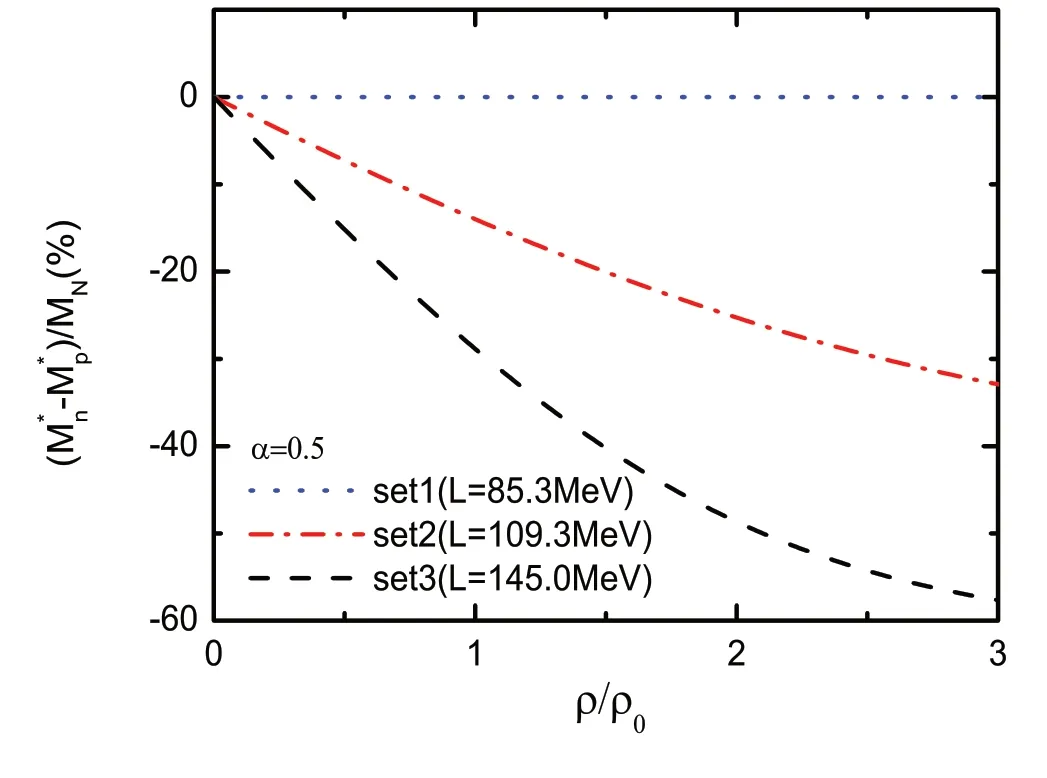
Fig.1 (Color online) Difference between neutron and proton effective masses as a function of the baryon density

Using the isospin asymmetry parameterα=(ρn−ρp)∕(ρn+ρp) , the symmetry energy can be written as [59]

Fig.2 (Color online) Symmetry energy as a function of the baryon density

In this study, we set the saturation density toρ0=0.16fm−3,and the binding energy per particle of the symmetric nuclear matter was set toE∕A−MN=−16 MeV.For symmetric nuclear matter, we set set1, set2, and set3 models to be the same as the result of vanishing isospin asymmetry.As shown in Table 1 and Fig.2, the symmetry energy of set1, set2,and set3 was set to be 31.6 MeV at the saturation density.Set1 contained onlyρmesons; however, set2 and set3 contained both theρandδmesons.For set1, when the symmetry energy was set to be 31.6 MeV at the saturation density,the coupling parametergρwas fixed, and the slope of symmetry was fixed atL=85.3 MeV.For set2 and set3, when the symmetry energy was fixed at 31.6 MeV, the slope of the symmetry energy was obtained by varying the coupling parametersgρandgδ.Because the effective massM∗of the above models for symmetric nuclear matter was the same,the symmetry energy with both theρandδmesons could not be softer than that of set1 containing onlyρmesons.To broaden the range of the slope parameters, we set the slope parameter of set2 and set3 to be 109.3 and 145.0 MeV by varying the coupling parametersgρandgδ, respectively.A broader range of slope parameters would be helpful for understanding the relationship between the properties of symmetry energy and the observables of heavy-ion collisions.The curvature of the symmetry energyKsym, which is a higher-order expansion coefficient of the symmetry energy compared to the slope parameterL, may also affect the properties of the symmetry energy and the observables of heavy-ion collisions at densities far beyond the saturation density.Ksymof set1, set2, and set3 is obtained as −15 , 141,and 391 MeV, respectively.

2.2 Relativistic quantum molecular dynamics approach

where 2Nconstraints satisfy the physical 6Nphase space.The sign ≈ indicates Dirac’s weak equality.The on-mass shell conditions can reduce the phase space from 8Nto 7Ndimensions.

Because only the constrainti=2Ndepends onτ,λis written as [77]

Assuming [φi,φj]=0 ,λi=0 forN+1＜i ＜2N[77].The equations of motion are then obtained as

Substituting Eq.(20) into Eq.(19), the scalar potentialSiand vector potentialViμof the nucleons can be obtained.For other hadrons, such as Δ resonances, similar to other transport models [34, 81], the Δ optical potential is estimated using the nucleon potentials and square of the Clebsch–Gordan coefficient.In the RQMD approach, the scalar density,isovector-scalar density, baryon current, and isovetor baryon current are expressed as

2.3 Dispersion relation and production of pions

The Hamiltonian of the mesons is defined as [48, 83–85]

andNMandNBare the total numbers of mesons and baryons,including charged resonances, respectively.The pion potential in the medium, which contains isoscalar and isovector contributions, is defined as

whereαdenotes the isospin asymmetry parameter, the coefficientCπis 36 MeV, the isospin quantityτis 1, 0, and -1 forπ−,π0, andπ+, respectively, andγπdetermines the isospin splitting of the pion potential and is set to two.In this study,the isoscalar part of pion potentialωisoscalarwas chosen as the Δ-hole model.The pion potential, which contains a pion branch (smaller value) and Δ-hole (larger value) branch, is defined as

The probabilities of the pion and Δ-hole branches satisfy the following equation:

where pRand pπare the momenta of the resonances and pions, respectively, andmRis the mass of the resonances.Because Δ0is uncharged, the Coulomb potential exists only for charged particles after the decay of Δ0.

The pion is generated from direct nucleon-nucleon collision and decay of the resonances Δ(1232) andN∗(1440).The reaction channels of the resonances and pions, which are the same as those in the LQMD model, are as follows[33, 48, 86, 87]:

For the production of the Δ(1232) andN∗(1440) resonances in nucleon-nucleon scattering, the parameterized cross sections calculated using the one-boson exchange model were employed [88].

The decay width of Δ(1232) andN∗(1440) , which originates from the p-wave resonances, is momentum-dependent and is expressed as [88]

where |p| is the momentum of the created pion (in GeV/c).The parametersa1,a2, anda3were taken as 22.48 (17.22)c∕GeV , 39.69 (39.69)c2∕GeV2, and 0.04(0.09) GeV2/c2,respectively, for Δ(N∗).The bare decay width of Δ(N∗) was given by Γ0=0.12(0.2)GeV.With the momentum-dependent decay width, the cross section of pion-nucleon scattering has the Breit-Wigner form:

Fig.3 (Color online) Rapidity distribution of the collective flows of free protons in the 197 Au + 197 Au reaction at an incident energy of 2.92 GeV/nucleon.The open circles correspond to the STAR data[94]

3 Results and discussion

The directed and elliptic flows were derived from the Fourier expansion of the azimuthal distribution:

Fig.4 (Color online) Rapidity distribution of the collective flows of free protons in the 108Sn+112 Sn reaction at an incident energy of 270 MeV/nucleon

Fig.5 (Color online) Rapidity distribution of the collective flows of free protons in the 132Sn+124 Sn reaction at an incident energy of 270 MeV/nucleon

Fig.6 (Color online) Difference between neutron and proton directed flows in the 108Sn+112 Sn and 132Sn+124 Sn reactions at an incident energy of 270 MeV/nucleon

With this LQMD.RMF model, the108Sn +112Sn and132Sn +124Sn collisions in this study were investigated at an incident energy of 270AMeV and an impact parameterb=3 fm.At an incident energy of 270AMeV, the nuclear matter of the collision center can be compressed to densities approaching 2ρ0.In this dense region, collective flows,which reflect nucleon–nucleon interactions, can be used to extract the high-density behavior of the EOS [1, 44, 79, 86,95].The collective flows of free protons in the108Sn +112Sn and132Sn +124Sn collisions are shown in Fig.4 and Fig.5,respectively.It is reasonable that the maximum value of the directed flowV1was significantly larger than that of the elliptic flowV2.In the same reaction system, the difference in the directed flows with various slopes of symmetry energy (set1,set2, and set3) was small.The difference in the elliptic flows with various slopes of symmetry energy was also small.To determine the relationship between the slope of the symmetry energy and the collective flow, we must process the collective flow data.

Fig.7 (Color online) Ratio between the π− and π+ yields as a function of the incident energy in the 132Sn+124 Sn reaction

Fig.8 (Color online) Transverse momentum spectra of pions as functions of transverse momentum at an incident energy of 270 MeV/nucleon.The left two panels a and b are the results of the 108Sn+112 Sn reaction, and the right two panels c and d are the results of the 132Sn+124 Sn reaction.The full circles correspond to the S π RIT data [40]

The difference between neutron and proton directed flows emitted from heavy-ion collisions can be used to extract the density dependence of the symmetry energy [86, 95].The difference between the neutron and proton directed flows is defined asV1n−V1p, as shown in Fig.6.The trend and shape of the difference between the neutron and proton directed flows were similar to those of nonrelativistic LQMD [86].For a given reaction system (nearly symmetric108Sn+112Sn system or neutron-rich132Sn+124Sn system), the absolute value of the difference between the neutron and proton directed flows with a soft symmetry energy was higher than that with a stiffsymmetry energy.Interestingly, the stiffness of the symmetry energy can be reflected through the difference between the neutron and proton directed flows.The relationship between the curvature of the symmetry energyKsymand the collective flows was then investigated.The difference betweenKsymof set1 andKsymof set3 was 406 MeV,which was significantly larger than the 59.7 MeV difference betweenLof set1 andLof set3.Although the curvature of the symmetry energyKsymalso affected the difference between the neutron and proton directed flows, because the nuclear matter of the collision center could only approach 2ρ0at an incident energy of 270AMeV, the effects ofKsymwere not significant compared to the effects of the slope parameterL.

In addition to collective flows, the production of isospin exotic particles such as hyperons, kaons, and pions can also be used to extract the symmetry energy [22–28].Because the thresholds of hyperons and kaons were not reached at the incident energies in this study, the isospin exotic particles were pions.First, we calculated the ratio between theπ−andπ+yields of the neutron-rich132Sn+124Sn system as a function of the collision energy at the impact parameterb=3fmandθcm＜90◦.Because set1 had the softest symmetry energy, it had the highest neutron density.Consequently, there were more neutron-neutron scatterings in set1,resulting in the production of more Δ−andπ−.As shown in Fig.7, theπ−∕π+ratio of set1 was the highest, and theπ−∕π+ratio of set2 was higher than that of set3.Specifically,at a collision energy of 270 MeV/nucleon, theπ−∕π+ratio without (with) theπpotential changed from 2.71 (2.54) to 2.23 (2.06) when the slope parameter was varied fromL=85.3 to 145.0 MeV, that is, from set1 to set3.In other words,theπ−∕π+ratio as a function of collision energy depends on the stiffness of the symmetry energy.This result was consistent with the predictions of most transport models [28,39, 90].When theπpotential was considered, the interaction betweenπand the nucleon became attractive, resulting in a decrease in bothπ−andπ+via the absorbed channelsπN→Δ(1232) and Δ(1232)N→NN.However, with theπpotential, because there were more neutrons in the neutronrich132Sn+124Sn system,π−was more easily absorbed thanπ+.Consequently, theπ−∕π+ratio without theπpotential was higher than that with theπpotential in the same RMF model.Moreover, it is worth mentioning that the threshold effect neglected in this study may cause theπ−∕π+ratio to be reversed.In other words, with the threshold effect [81, 90,91],π−∕π+of set3 may be the highest, and theπ−∕π+ratio of set2 may be higher than that of set1.

Fig.9 (Color online) Single spectral ratios of pions as functions of transverse momentum for the 108Sn+112 Sn and 132Sn+124 Sn reactions at an incident energy of 270 MeV/nucleon.The full circles correspond to the S πRIT data [40]

Next, the properties ofπwere predicted as a function of the transverse momentum.As shown in Fig.8, the left and right panels are the transverse momentum spectra of pions for the nearly symmetric108Sn+112Sn and neutron rich132Sn+124Sn reactions atθcm＜90◦, respectively.In collisions between isotopes,π+is mainly generated from collisions between protons andπ−is mainly generated from collisions between neutrons.Theoretically, a stiffer symmetry energy would have a stronger repulsive force to push out neutrons and a stronger attractive force to squeeze protons, resulting in a decrease in theπ−yield and an increase in theπ+yield, respectively.As shown in panels (b) and (d) of Fig.8, the stiffer symmetry energy indeed led to larger transverse momentum spectra forπ+.However, the relationship between the transverse momentum spectra ofπ−and the stiffness of the symmetry energy could not be directly explained.Compared with the stiff-ness of the symmetry energy, theπpotential had a more significant impact on the transverse momentum spectrum ofπ.For the neutron-rich132Sn+124Sn system, the transverse momentum spectra of bothπ+andπ−without theπpotential were lower than those of the SπRIT data atpT≲200 MeV.When theπpotential was considered, the transverse momentum spectra of bothπ+andπ−increased atpT≲200 MeV but decreased atpT≳200 MeV.Consequently, the transverse momentum spectra ofπ+with theπpotential were almost consistent with the SπRIT data [40];however, the transverse momentum spectra ofπ−were still lower than the SπRIT data for the entirepTdomain.The lower transverse momentum spectra ofπ−may be due to the absence of a threshold effect.The threshold effect,which was not considered in this study, may enhance the production ofπ−[81, 90, 91].

Fig.10 (Color online) Double ratio of pions as a function of transverse momentum at an incident energy of 270 MeV/nucleon.The full circles correspond to the S πRIT data [40]

Because a stiffer symmetry energy would have a stronger repulsive force to push out neutrons and a stronger attractive force to squeeze protons, resulting in a decrease in theπ−yield and an increase in theπ+yield, respectively,the single ratio SR(π−∕π+)=[dM(π−)∕dpT]∕[dM(π+)∕dpT]may depend on the stiffness of the symmetry energy and the reaction system.As shown in Fig.9, for both the nearly symmetric system and neutron-rich system,a softer symmetry energy led to a larger single ratio.In addition, for the same stiffness of the symmetry energy,because the neutron-neutron scattering of the neutron-rich132Sn+124Sn system was greater than that of the nearly symmetric108Sn+112Sn system, the single ratio of the neutron-rich system was higher than that of the nearly symmetric system.It is worth mentioning that the single ratio of108Sn+112Sn was almost consistent with the experimental data.However, the single ratio of132Sn+124Sn was lower than that of the experimental data for the entirepTdomain.This was because the transverse momentum spectraπ−of132Sn+124Sn were lower than the experimental data.

The double ratio between the neutron rich system and the nearly symmetr ic system DR(π−∕π+)=SR(π−∕π+)132+124∕SR(π−∕π+)108+112, which can cancel out most of the systematic errors caused by Coulomb and isoscalar interactions, was suggested to extract the properties of the symmetry energy [40].However, because a lower symmetry energy will lead to a larger single ratio for both the nearly symmetric system and neutron-rich system, as shown in Fig.10, it is still difficult to understand the dependence of the double ratio on the stiffness of symmetry energy.In addition, the double ratio without theπpotential decreased slightly as a function of the transverse momentum, whereas it increased slightly as the transverse momentum increased when theπpotential was considered.However, the increasing trend was still considerably weaker than that of the experimental results.The lower double ratio originated from the lower single ratio of the neutron-rich132Sn+124Sn system compared with the experimental data.The threshold effect may enhance the production ofπ−[81, 90, 91] and the single ratio of the neutron-rich system, resulting in a larger double ratio.

4 Conclusion

An RMF with various symmetry energies, namely set1,set2, and set3, was implemented in LQMD.The collective flows of the nearly symmetric108Sn+112Sn and neutron-rich132Sn+124Sn systems were successfully generated from the LQMD.RMF.It has been observed that the directed flowV1was an order of magnitude larger than the elliptic flowV2.However, the difference between the directed flowsV1with various slopes of symmetry energy was small.The difference in the directed flowsV2with various slopes of symmetry energy was also small.To explore the relationship between the collective flow and the stiffness of the symmetry energy, we defined the difference between neutron and proton directed flowsV1n−V1p.For a given nearly symmetric system or neutron-rich system, the absolute value ofV1n−V1pincreased with decreasing slope of the symmetry energy.

We also investigated the relationship between isospin exotic particles and the stiffness of the symmetry energy.The ratio betweenπ−yield andπ+yield of the neutron-rich132Sn+124Sn system as a function of the collision energy increased with a decrease in the slope parameter of the symmetry energy.At an incident energy of 270 MeV/nucleon, the properties ofπwere predicted as a function of the transverse momentum.For the nearly symmetric108Sn+112Sn system,the single ratio of the nearly symmetric system was consistent with the experimental data.However, for the neutron-rich132Sn+124Sn system, the single ratio was lower than the experimental data, resulting in a double ratio lower than the experimental data.Theπpotential did not explain the lower transverse momentum spectra ofπ−in the neutron-rich system.Considering theπpotential, the double ratio increased slightly with increasing transverse momentum.However, the increasing trend was still considerably weaker than that observed in the experimental results.The single ratio of the neutron-rich system and the double ratio may be lower than the experimental data because of the lack of a threshold effect.The threshold effect, which can enhance the production ofπ−, could be a candidate for enhancing the single ratio of the neutron-rich system to a double ratio.Moreover, because a softer symmetry energy led to a larger single ratio for both nearly symmetric and neutron-rich systems, the dependence of the double ratio on the stiffness of the symmetry energy was not significant.The sensitivity of the double ratio to the stiffness of the symmetry energy may also be due to the lack of a threshold effect.When the threshold effect is considered, the production ofπ−in a neutron-rich system may be more significant than that in a nearly symmetric system.In the future, when collective flows, the single ratio of the neutron-rich system and the double ratio of the LQMD.RMF are consistent with the experimental data,V1n−V1pand the single ratio of the neutron-rich systemπ−∕π+, which are sensitive to the stiffness of the symmetry energy, may be used to extract the slope parameter of the symmetry energy.

Appendix A: Details of equation of motion

Declarations

Conflicts of interestThe authors declare that they have no competing interests.

Author ContributionsAll authors contributed to the study conception and design.Material preparation, data collection, and analysis were performed by Si-Na Wei and Zhao-Qing Feng.The first draft of the manuscript was written by Si-Na Wei, and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Data AvailibilityThe data that support the findings of this study are openly available in Science Data Bank at https:// cstr.cn/ 31253.11.scien cedb.j00186.00359 and https:// doi.org/ 10.57760/ scien cedb.j00186.00359.