一道高考线段比值问题的一般化推广
福建省厦门第一中学 (361003) 陈 恬
1.试题解析
2022年全国甲卷数学第16题考查解三角形、函数最值等内容,考查直观想象、数学运算、逻辑推理等核心素养.
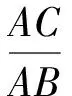
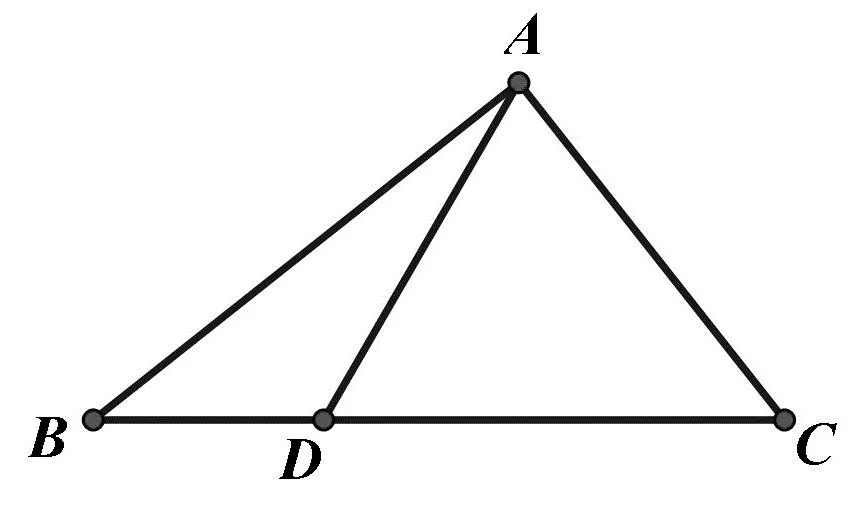
图1
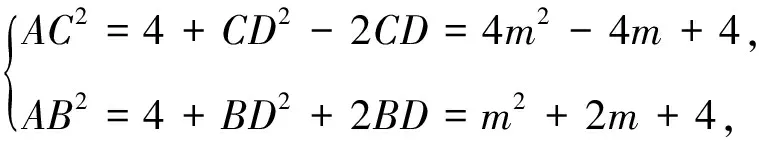
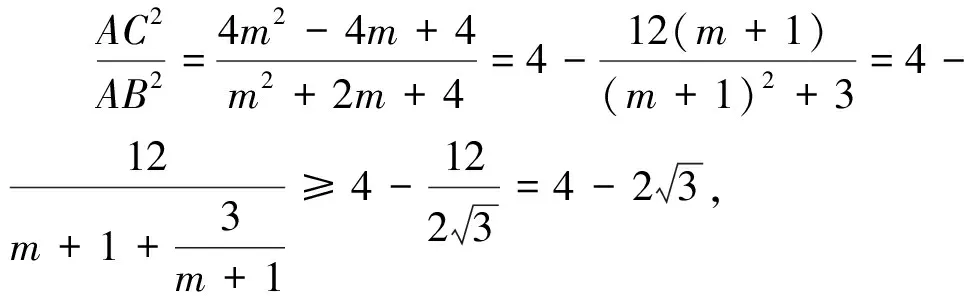
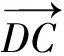
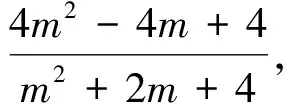
2.试题转化

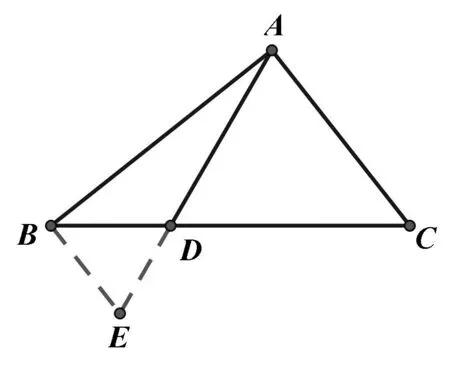
图2
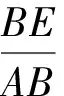
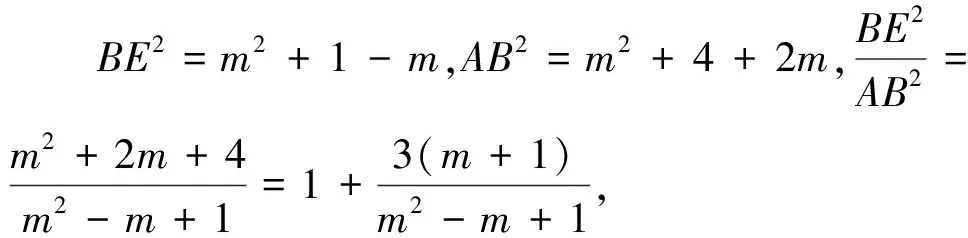
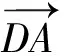
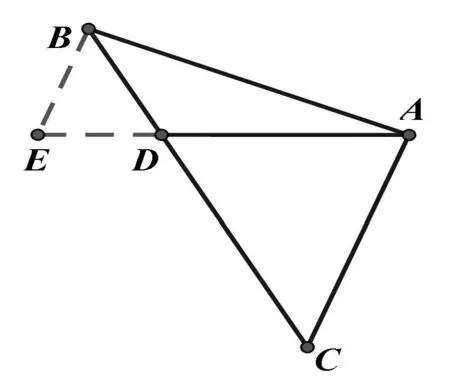
图3
注意到此处要对2x-1的符号进行讨论:
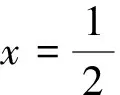
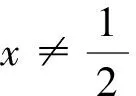
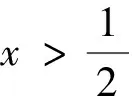
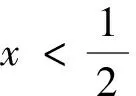
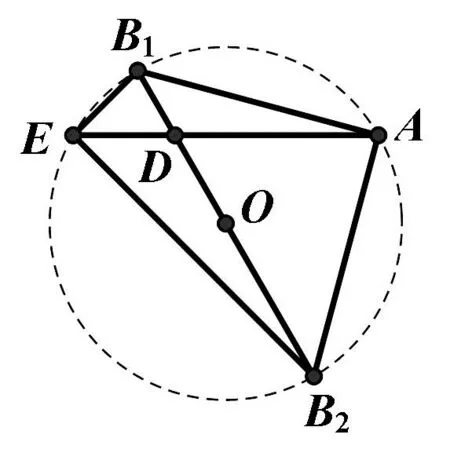
图4
这个结论非常优美,几何构造也非常简单,从直观上很容易想到背后可能存在更一般化的几何性质.进而思考当线段的比值改变或夹角改变的情况下,结论是否成立.
3.一般化推广
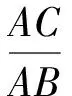
3.1 推广结论的验证
分析:由于给出的条件是一般化的,结论是否成立还不确定,想要从平面几何直接处理是有难度的,采用解析几何运算来定量分析;又考虑到需要找到点A的位置,因此借助直线参数方程来解决.
解析:如图5,以D为原点,以BC为x轴,建立平面直角坐标系.设B(-m,0),C(n,0).先考虑特殊情况:
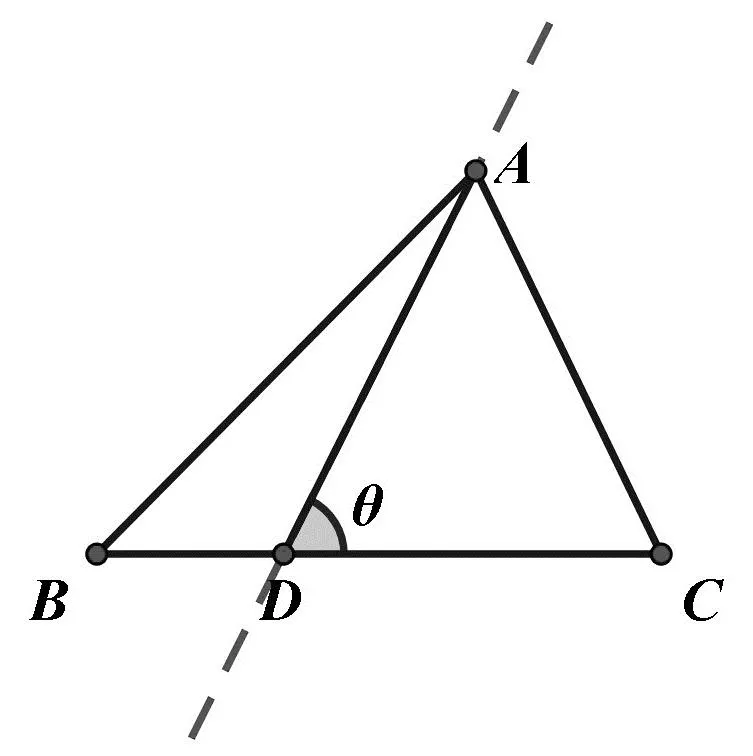
图5
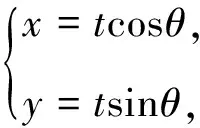
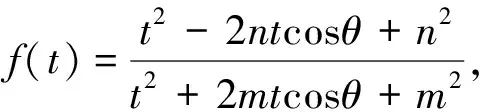
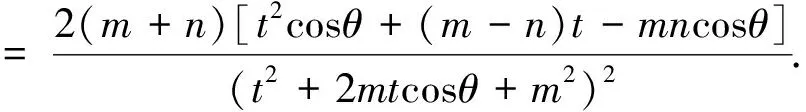
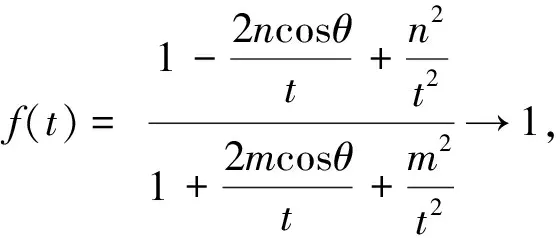
结合参数方程的几何意义,进而探究t1,t2的具体涵义.
我国历史上最大的一部大型丛书是乾隆三十七年(1772年)下诏纂修的《钦定四库全书》。《四库全书》编成后,共抄写七部,分别建立七座藏书楼进行收藏,总称为“四库七阁”。 其中,紫禁城的文渊阁、奉天故宫(今沈阳)的文溯阁、圆明园的文源阁、承德避暑山庄的文津阁被称为“内廷四阁”。 镇江金山寺的文宗阁、江都大观堂(今扬州市)的文汇阁和杭州西湖行宫的文澜阁,被称为“江浙三阁”。
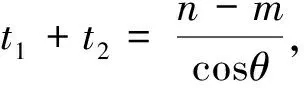
推广结论如图6,在△ABC中,已知边BC上一点D,BD=m,CD=n,∠ADB=θ,其中m≠n且0°<θ<180°.则
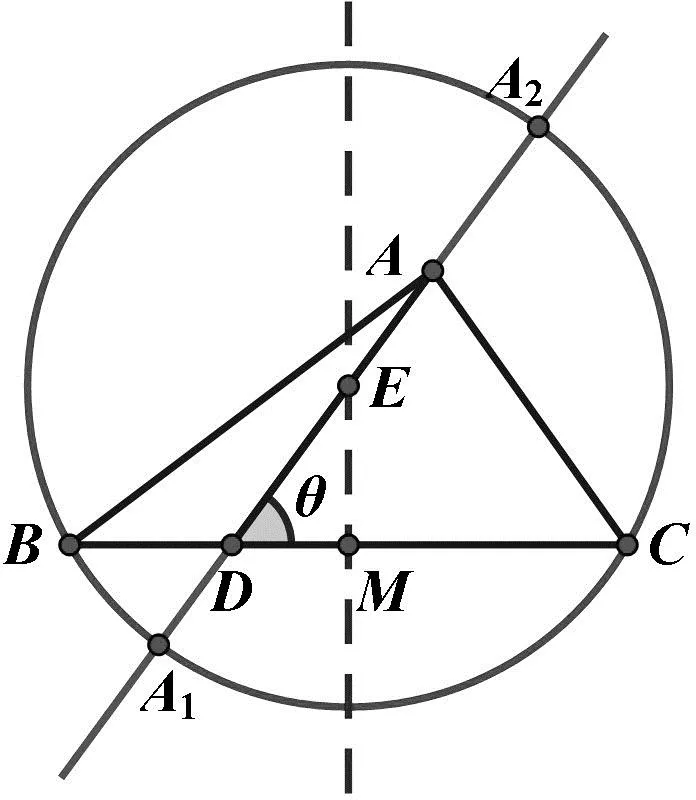
图6


当然,可以将θ为直角时的情况看作圆心E在无穷远处,半径为无穷大,则A1对应是D点,A2对应无穷远点处.
3.2 推广结论的平几探索
上述方法虽然能够准确得到取值的变化规律,但对于只求最值的问题来说相对复杂.在得到结论的基础上,尝试用平面几何方法找出最值位置.
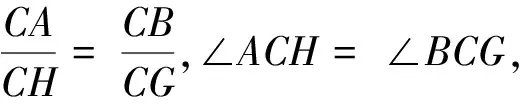
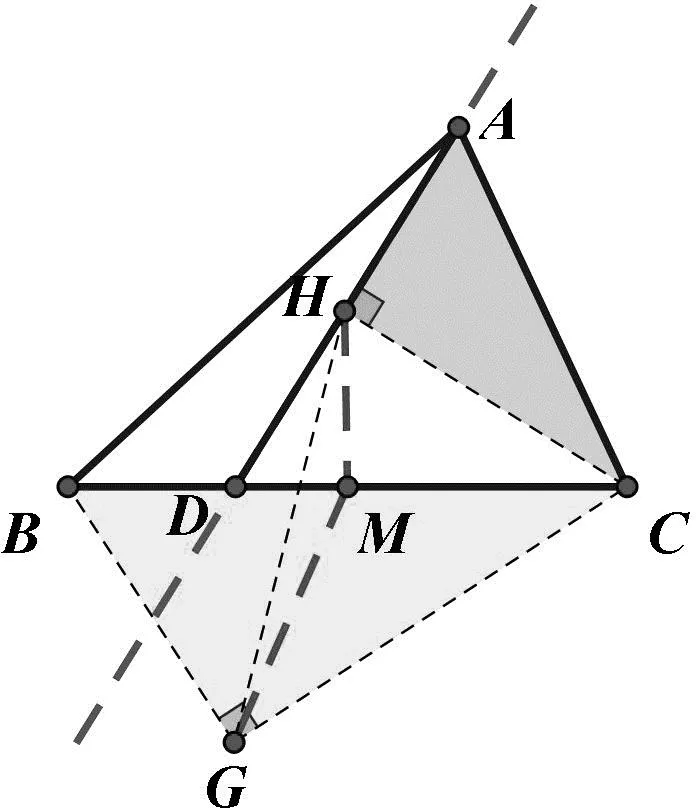
图7
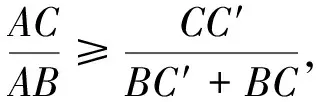
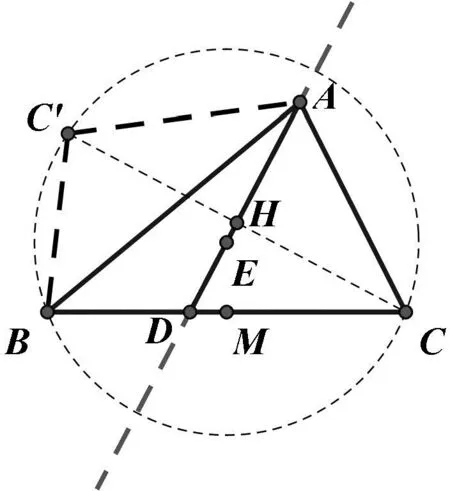
图8
同理可得当θ为钝角时的情况.
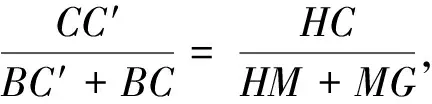
4 结语
直观想象核心素养是高考考查的重要内容,几何中的最值问题往往存在一个更一般化的几何性质作为命题背景,教师与学生在日常教学中不应只停留在解出问题的表面,还应该鼓励师生进行深入探索,培养坚忍不拔的探索精神,形成做研究的习惯,促进数学学科素养的提升.

