考虑降水入渗和径流的边坡稳定性分析

付建利，路玉恒

(德州黄河河务局齐河黄河河务局，山东 德州 251100)

1 工程背景

某灌区内天然植草路堑边坡发生破坏，斜坡主要由两个台阶组成，破坏发生在上部台阶。根据近期的气象遥测系统，距离研究地点10 km的自动气象数据采集系统记录了大量的融雪和降雨。此外，斜坡沿坡有排水系统以排出地表水流，但在边坡失稳发生时，由于落叶、沉积物和积雪的堵塞，观察到排水沟处有水溢出，经判断是斜坡破坏的主要原因之一[1]。

2 模拟方法

本文针对此边坡失稳现象进行了稳定性分析，并建立了用于边坡稳定性评估的三维模型，进行了地表径流和土壤水流分析，仅考虑实际路堑边坡的上部台阶和具有沟渠堵塞点的沟渠系统。模型由土壤和草层两部分组成，草层厚度为0.2 m。土壤的干密度为968 kg/m3，有效内聚力为1.0 kPa，有效摩擦角为32°，弹性模量为4.6 MPa，泊松比为0.3，饱和透水性为3.30×10-5m/s，饱和体积含水量为0.61 m3/m3。根据当地水文气象资料测得的平均值，地下水位的初始条件设定为距地表5.0 m。地表径流边界条件采用流入边界和流出边界来模拟，在排水沟未堵塞的情况下，流入水量等于流出水量[2-5]。而在排水沟堵塞的情况时，流入水量值保持不变，流出流量值变为零。设置沟渠系统的侧面和底部为零流量边界。此外，排水沟的进水仅考虑了来自聚集区的径流，没有考虑来自坡顶的渗透水，坡顶设置为零流量边界。水量定义为流入流量值，如式(1)：

Q1=(P+S)×A；Q2=αQ1

(1)

式中：Q1为流入流量值，m3/s；P为降雨量，m/s；S为融雪水量，m/s；A为计算面积，m2；Q2为流出流量值，m3/s；α为与堵塞率相关的参数，取0～1(1对应于水从沟渠系统排出的情况、没有堵塞，0对应沟渠系统被堵塞并且水从侧面流出的情况、完全堵塞)。

3 结果和讨论

3.1 气候条件和总流入水量

图1为降雨量随时间的变化，降雨主要集中在10～25 h时期，在18 h时降雨量最大，为6.72 mm/h。图2为积雪深度随时间的变化，积雪深度呈现逐渐下降的趋势，在降雨发生后积雪深度明显下降。图3为总流入水量，总流入水量先增大后减小，在降雨发生后，总流入水量显著增加，在18 h后随着降雨量的减小以及积雪深度的持续减小反而呈现下降的趋势。根据雪深和降雪量的数据估算融雪水量。从理论上讲，积雪深度可以通过积雪模型来估计，使用平均气温来确定雨或雪的降水量。为了获得更准确的结果，通常采用气象监测数据，即测量的雪深和降雪数据来估计融雪量。通过考虑边坡失稳前的降雨历史资料进行初始渗流分析，以获得边坡破坏前一天时边坡中的初始含水量分布。通过考虑地表径流和土壤水流的耦合模型，以1 h为时间步长，对边坡失稳时25 h内气候边界条件下的瞬态渗流进行分析，以自重计算模型的初始平衡条件。最后，结合孔隙水压力和含水量分布进行边坡破坏分析，计算边坡的局部安全系数。

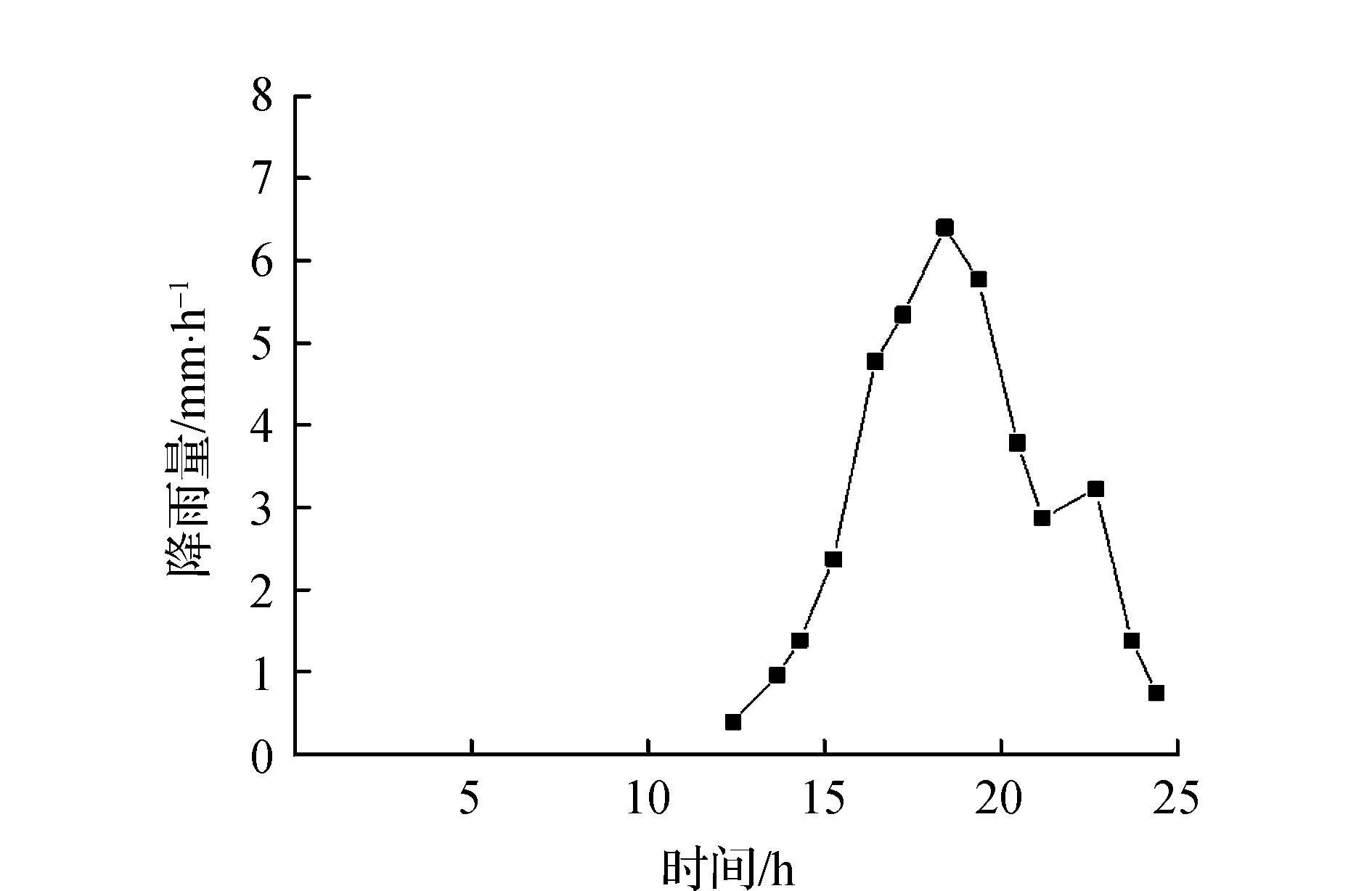
图1 降雨量随时间变化规律

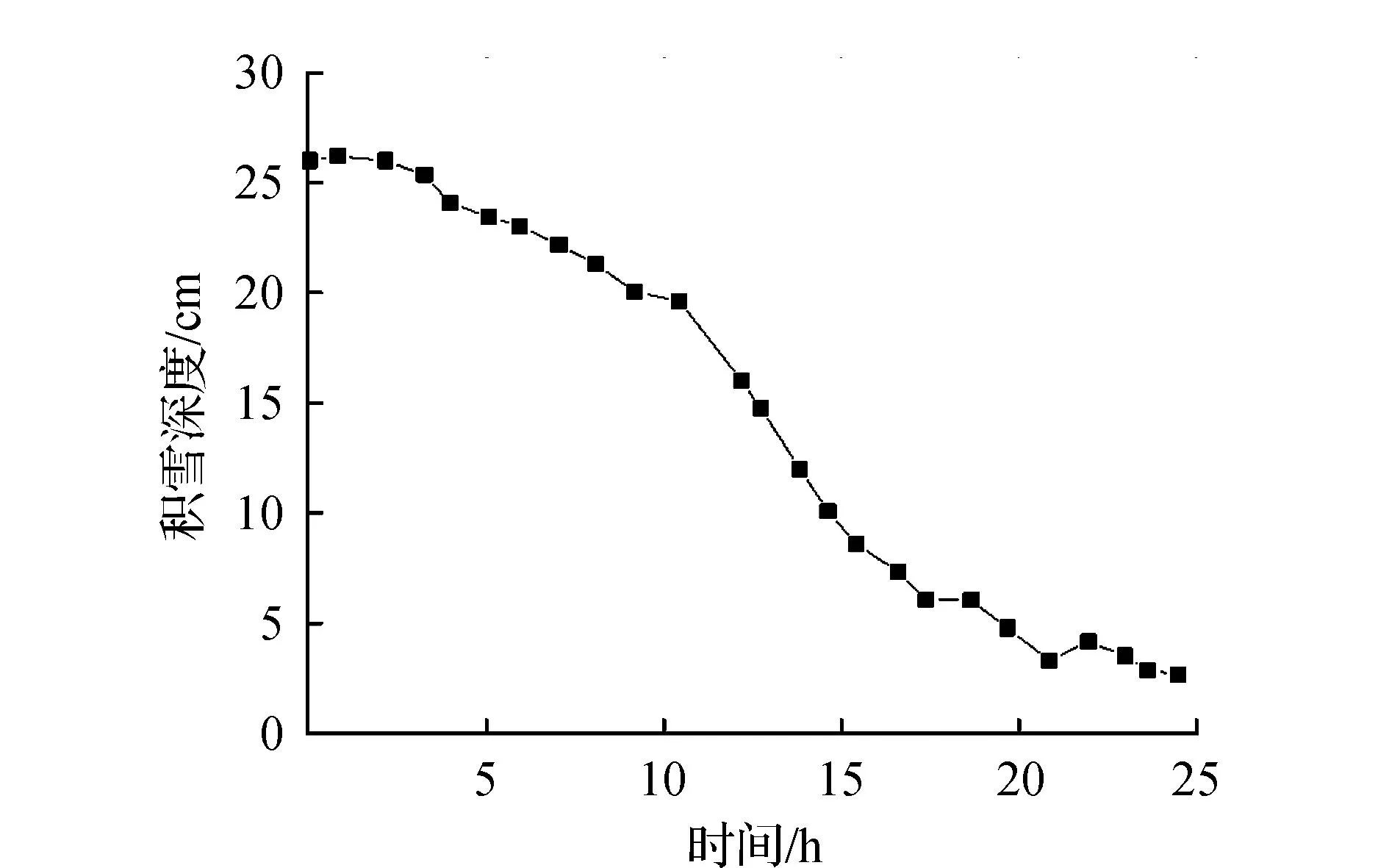
图2 积雪深度随时间变化规律

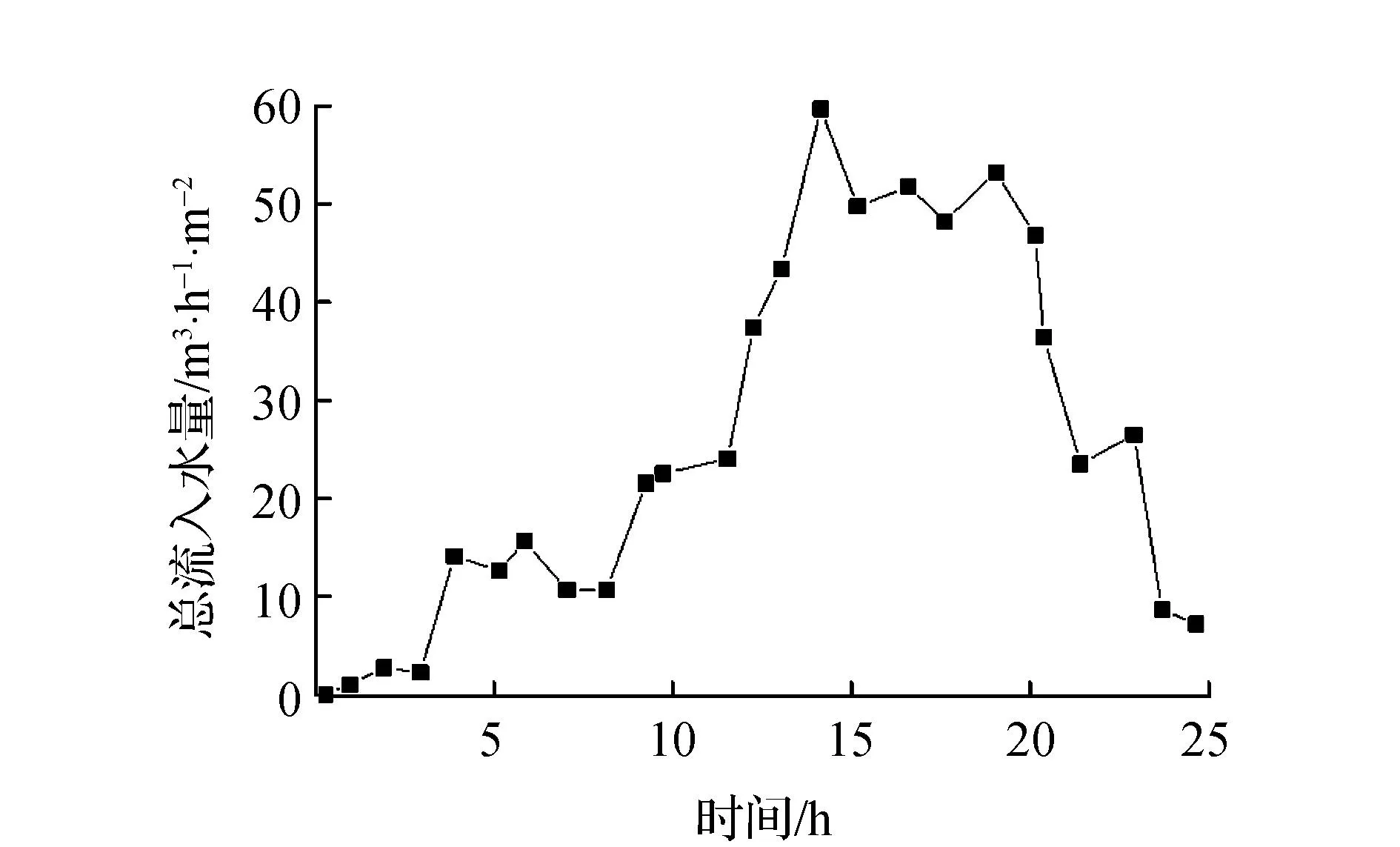
图3 总流入水量随时间变化规律

3.2 溢流对边坡稳定性的影响

本研究中仅考虑裸露土壤，评估沟渠堵塞引起的溢流对边坡稳定性的影响，比较了边坡失效时的表面流深度分布以及完全堵塞(α=0)和无堵塞(α=1)的情况下模拟结果。在沟渠完全堵塞的情况下，排水系统的溢流从边坡表面的侧面产生，此时降雨和融雪水无法通过排水沟顺利排出。相反，沟渠中的水被完全排出时则不会堵塞沟渠。完全堵塞和无堵塞的两种情况下边坡的孔隙水压力分布也呈现不同的结果，有溢流时，在斜坡地面以下较深的地方仍呈现出正向增加的孔隙水压力。在没有堵塞的情况下，地表浅层孔隙水压力为正向增加，大部分深层斜坡区域仍是负孔隙水压力。比较完全堵塞和无堵塞的情况下边坡的局部安全系数的分布，在完全堵塞的情况下，大部分边坡区域处于不稳定状态，在沟渠堵塞点的横截面不稳定深度接近2.2 m。相反，在没有堵塞的情况中，尽管坡面上出现了较低的局部安全系数区域，但沿坡并没有明显的破坏区域[6-7]。

有效饱和度、孔隙水压力、局部安全系数和径流速度随时间的变化如图4～图7所示。由图4、图5可知，水的渗透会导致有效饱和度和孔隙水压力的增加，从而导致未饱和土壤的吸水性减小，并最终降低局部安全系数，如图6所示。由图4可知，在α=1的情况下，排水沟渠内无堵塞，有效饱和度相对较稳定，在0.5～0.6范围内逐渐上升。在α=0的情况下，排水沟渠内堵塞严重，在降雨7 h后快速上升并稳定在1.0。由图5可知，孔隙水压力随时间的变化规律与有效饱和度较为相似，在α=1的情况下，孔隙水压力在-8.0～-5.0 kPa范围内逐渐上升，恒为负值。在α=0的情况下，排水沟渠内堵塞严重，孔隙水压力快速上升最终出现了正值的孔隙水压力。由图6可知，局部安全系数均随时间的增加而下降，但在溢流导致沟渠堵塞的情况下，有效饱和度和孔隙水压力的增加以及局部安全系数的减少更为显著。由此可知，沟渠堵塞增加了边坡破坏失稳的风险，溢流是导致边坡失稳的关键因素，在实际工程中应重视溢流对边坡稳定性的影响。经计算，沿坡面的边坡临界侵蚀速度为0.26 m/s，图7显示了完全堵塞情况下边坡的径流速度，径流速度超过了临界侵蚀速度，最终导致边坡的侵蚀破坏，影响边坡的稳定性。沟渠堵塞情况下，溢流渗透到边坡中，土壤的含水量急剧增加导致边坡加速破坏。当排水系统工作性能良好时，在实际情况下边坡基本可以保持稳定性。

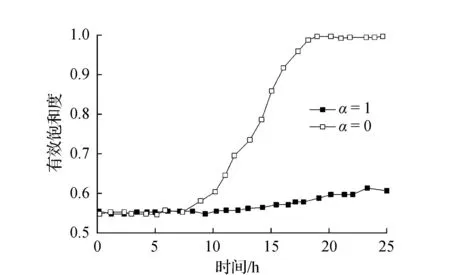
图4 有效饱和度随时间变化规律

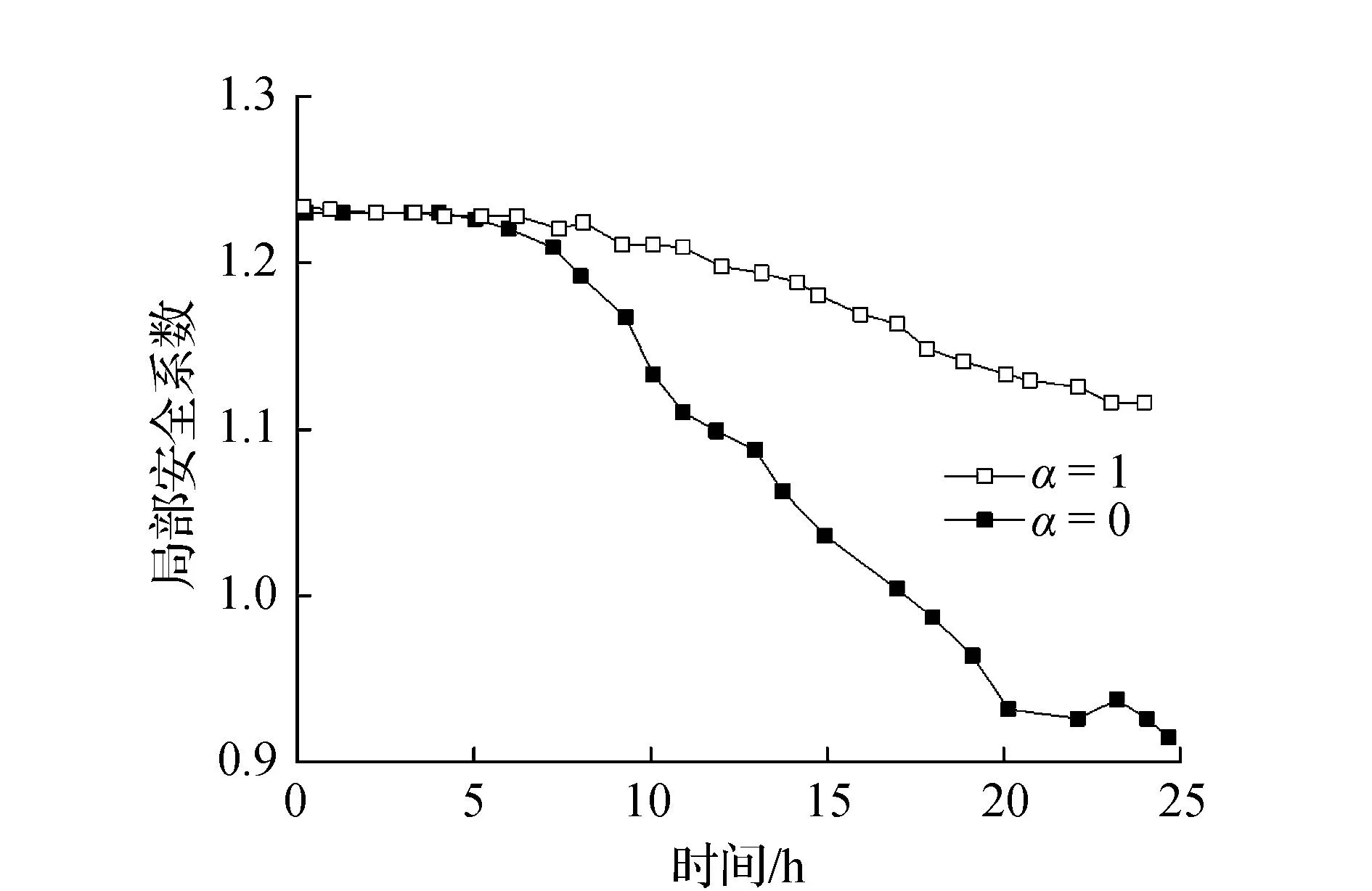
图6 局部安全系数随时间变化规律

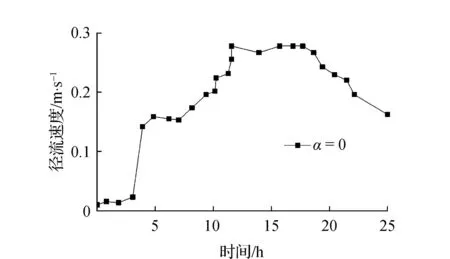
图7 径流速度随时间变化规律

3.3 草层对边坡稳定性的影响

地表草层在边坡稳定性分析中起着重要作用，利用植物根系等进行生态防护是环境友好的边坡防护方案之一，可以增加降雨引起的浅层土壤边坡的稳定性。与裸露土相比，植被土具有明显不同的渗透性能和力学性能。相较于裸露土，在植被土壤中有更高的持水能力和更低的渗透系数。同时，植被根系具有固定土壤颗粒的作用，减弱边坡表面侵蚀程度，植被根系穿过潜在的破坏面可提高边坡稳定性。有学者进行了渗透性试验对比草地和裸露土壤的饱和渗透系数的区别，图8为不同根系体积比的草地和裸露土壤的饱和渗透系数比值[8]。由图8可知，在根系体积比为0.002 m3/m3时，饱和渗透系数比值为1.03。饱和渗透系数比值随根系体积比的增加而逐渐降低。

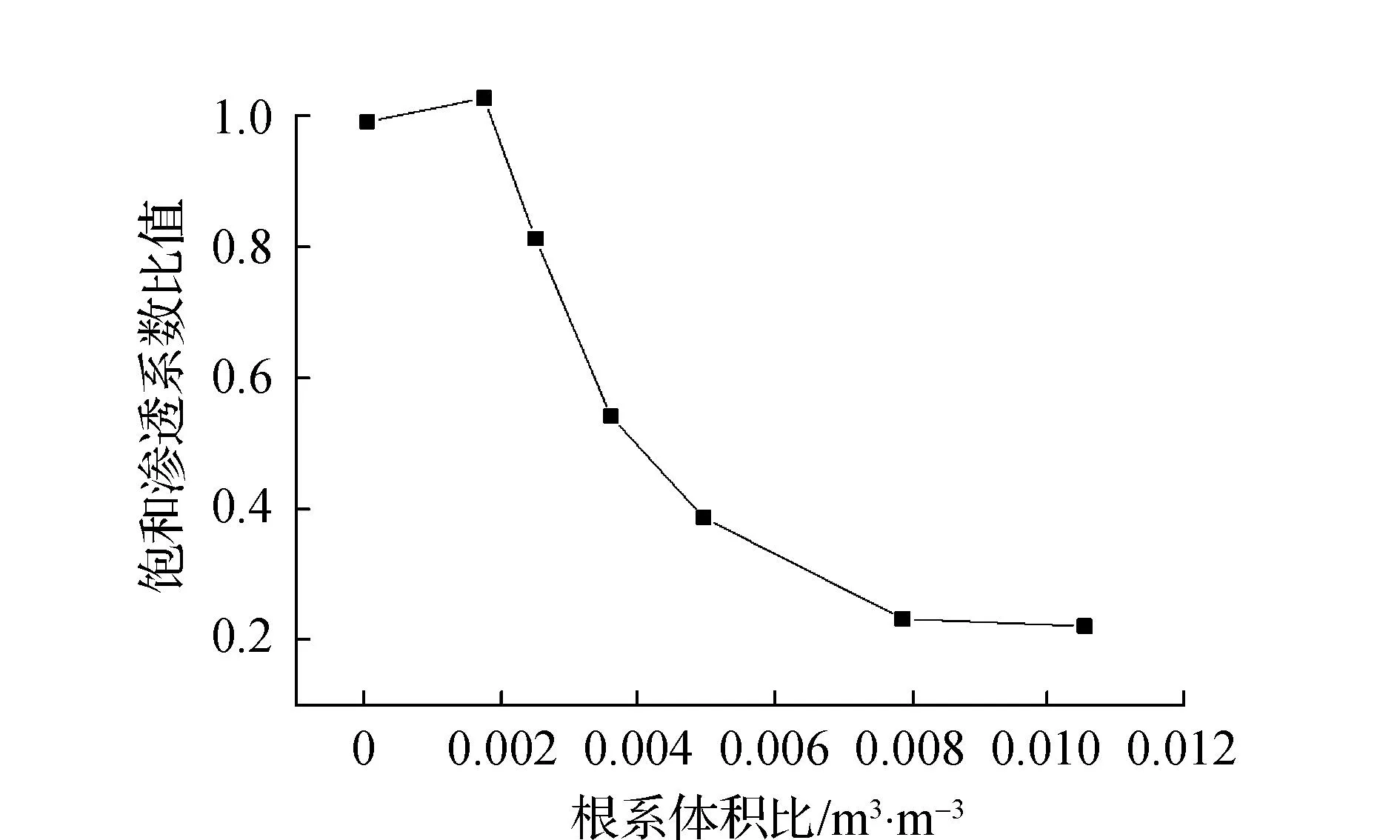
图8 不同根系体积比下饱和渗透系数比值变化规律

由图8可以看出，随着根系体积比的增加，由于更多的根系堵塞了土壤孔隙，草地土壤的渗透性减小。本研究中的边坡破坏发生在10月底，考虑到春季的草类植物的生长，假定草龄为8个月。根据图8的草层饱和渗透系数，为评价Ks(正负样本分隔程度的评价指标)值的影响，在考虑草龄效应的情况下，在模拟中采用0.25和0.50的比例。根据草龄校准草层的有效内聚力，4个月草层的有效内聚力为4.2 kPa，8个月草层的有效内聚力为8.1 kPa，曼宁系数值取为0.3 s/m1/3。为了简化，其他参数设置与裸露土相似。所有模拟都是在沟渠堵塞条件下进行的。

分析有草层的边坡孔隙水压力和局部安全系数的分布，与仅考虑裸露土壤的情况相比，草层有效地阻碍了渗透，并减少了湿润土层的深度。相应地，破坏规模显著减小，模拟结果证明了草层对边坡具有保护作用。在理论上，不同草龄均具有一定的保护作用。当采用0.25的比率时，模拟滑面比实际滑面浅。由于根部腐烂导致大孔隙的形成，在一定程度上导致渗透性的增加。考虑到破坏时间在秋季，部分根系可能会腐烂，导致根系体积比降低，从而增加饱和渗透系数比。考虑根腐效应时，模拟的破坏深度为1.5 m，大致达到实际滑面，但此时忽略了溢流引起的侵蚀效应。

4 结 论

(1)沟渠堵塞引起的径流外溢对边坡稳定性有不利影响，在溢流导致沟渠堵塞的情况下，有效饱和度和孔隙水压力的增加以及局部安全系数的减少更为显著。堵塞情况下边坡的径流速度超过了临界侵蚀速度，最终导致边坡的侵蚀破坏。溢流是导致边坡失稳的关键因素。

(2)草层通过限制地表入渗和增强土壤强度，可以增加降雨引起的浅层土壤边坡的稳定性。饱和渗透系数比值随根系体积比的增加而逐渐降低。同时，草层的性质受到草龄和根部腐烂等多种因素的影响，可能会产生相反的影响。

(3)通过考虑土壤、草层等不同材料对渗透和径流的影响，本研究可以为强降水条件下的边坡稳定性和防护方法提供有价值的信息。