航天器受控绕飞任务规划与自主通用软件实现
张 赛, 杨 震∗, 王 华, 罗亚中
(1.国防科技大学空天科学学院, 长沙 410073; 2.空天任务智能规划与仿真湖南省重点实验室, 长沙 410073)
1 引言
太空是世界大国博弈新焦点和战略竞争制高点[1],美、俄等航天大国为增强太空主导权与控制权,发射大量重要战略卫星以支撑空间态势感知、空间对抗和空间支援等太空攻防任务[2⁃3]。 其中,以在轨操控为基础的在轨服务任务[4]方兴未艾,相关核心技术仍有待进一步发展。
为实现长期稳定的在轨服务,服务航天器通常需要和目标航天器形成稳定的相对构型,包括伴飞构型、悬停构型和绕飞构型等[4⁃5]。 其中,服务航天器通过绕飞构型可实现对目标航天器的全方位监测,在航天器在轨检查与监视、空间目标识别与侦察、辅助航天员舱外活动、编队飞行、空间交会对接等空间活动中具有重要应用价值和实际工程意义[6⁃7]。 由于航天器携带燃料有限,导致其变轨范围有限,因此在实施变轨机动时需提前进行轨道任务规划,以明确行动路线和机动策略。针对特定问题,部分科研院所开发了特定的仿真规划软件,如预警星座设计系统[8]、逃逸与应急救生仿真系统[9]、交会对接系统[10]和近距离相对运动系统[11]等。 对于航天器的在轨服务任务,其实现过程是多种相对运动方式的组合,因此离不开任务的全流程轨道规划。 由于与工程实际结合紧密、任务组合段多,导致轨道规划求解时的动力学复杂、约束多且收敛难。 该类近距离相对运动的规划依旧存在困难,现阶段少有软件实现了对该问题的通用求解。
在航天仿真分析领域,处于绝对领先地位的商业化分析软件是美国AGI 公司开发的STK(System Tool Kit)软件,其能够实现空间环境、卫星、导弹等与基础航天动力学相关的所有领域仿真分析与评估[12⁃13]。 近期,针对航天器交会和近距离操控(Rendezvous and Proximity Operation,RPO)问题,STK 在新版本中更新了RPO 功能,能够实现对多种近距离相对运动的一体化规划求解。 国内在航天动力学软件方面起步较晚,主要工作可分为3 类:解决特殊问题的工程软件[10]、面向一般航天任务的仿真分析软件[14]和基于商业软件二次开发的软件[8],这些软件在核心算法性能、通用性、友好性等方面与国外软件有较大差距[14]。
通用航天任务设计软件是总体、轨道、测控、运营等专业的核心工具,贯穿航天任务方案论证、生产部署、任务运营等全寿命周期,目前国内尚缺乏成熟的工业级产品。 基于此,由国防科技大学空天科学学院研制的航天任务设计工具箱ATK(Aerospace Tool Kit)解决了软件总体架构设计、航天动力学模型算法库集成、轨道机动规划通用化建模与求解等关键技术,初步实现了标准平台、二/三维可视化、基于脚本语言的二次开发、卫星轨道高精度预报、卫星星座设计、可见性与覆盖分析、轨道机动规划等功能,具备了初步的航天任务分析与设计能力。 其中通用轨道机动规划工具能对航天器交会对接、探月多阶段轨道设计、航天器近距离交会与操控等典型复杂航天任务进行轨道机动参数规划。
面向在轨服务等空间操控任务需求,本文给出了航天器多脉冲机动绕飞任务的轨迹设计和规划方法,基于ATK 通用轨道机动规划工具实现了接近和绕飞全流程的规划和仿真,并进一步分析了任务参数对燃料消耗的影响。
2 动力学模型与软件介绍
2.1 坐标系定义
坐标系示意图如图1 所示。 定义J2000 地心惯性坐标系SJ(OJ-xJyJzJ) :坐标原点OJ在地球中心,xJ轴沿地球赤道面和黄道面的交线,指向春分点γ,zJ轴和地球自转轴重合并指向北极,yJ轴根据右手法则得到。 定义航天器LVLH(Local Vertical, Local Horizontal)坐标系Sp(Op-xpypzp):原点Op位于航天器质心,xp轴沿航天器矢径方向,yp轴位于轨道平面内沿速度方向且与xp轴垂直,zp轴垂直轨道面并与xp、yp轴构成右手直角坐标系。
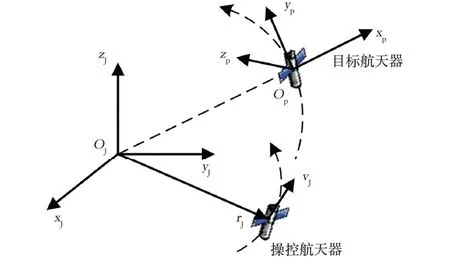
图1 坐标系位置关系示意图Fig.1 Illustration of defined coordinates
2.2 轨道动力学模型
在二体问题中,假设航天器的引力场是与距离的平方成反比的中心引力场。 但现实情况中航天器的轨道会受到地球形状的不均匀、大气阻力、太阳辐射压力等各种因素产生的摄动力影响,导致其偏离圆锥曲线。 考虑摄动力时,航天器在地心惯性系下的绝对轨道运动方程[15]为式(1)。
式中,μ为中心天体引力常数,r和v分别为航天器的位置和速度矢量,r=‖r‖为航天器的地心距,u是为航天器的推力加速度,a为航天器的各种摄动加速度的总和,包含非球形引力摄动加速度agrav、大气阻力加速度adrag、第三体(太阳、月球等)引力加速度a3-body、太阳光压加速度aSBR、以及地月潮汐力等其他的摄动加速度aothers。
如图1 所示,目标航天器LVLH 坐标系Sp(Op-xpypzp)是一个动坐标系。 定义服务航天器在坐标系Sp中的位置速度矢量为,基于式(1)和坐标系变换可推导出服务航天器在坐标系Sp中的相对运动方程[16]为式(2)。
其中,ω和Rt分别为目标航天器的轨道角速度和地心距,ux、uy和uz为服务航天器在坐标系Sp下的推力加速度分量,ax、ay和az为服务航天器的摄动加速度分量。
2.3 通用轨道机动规划工具介绍
ATK 软件的通用轨道机动规划工具是用于交互式轨道机动和轨迹设计的软件工具,支持高精度轨道外推、脉冲推力机动建模和连续推力机动建模,通过执行任务控制序列(Mission Control Sequence, MCS)计算得到航天器星历。
任务控制序列定义了卫星的一系列控制机动,主要由初始段、预报段、机动段、瞄准序列段、停止段和返回段等多个基本段组成。 其中瞄准序列段可根据设定的目标和自变量,利用微分修正或序列二次规划方法自动寻找满足约束的自变量值,是机动规划的核心,其计算流程如图2 所示。
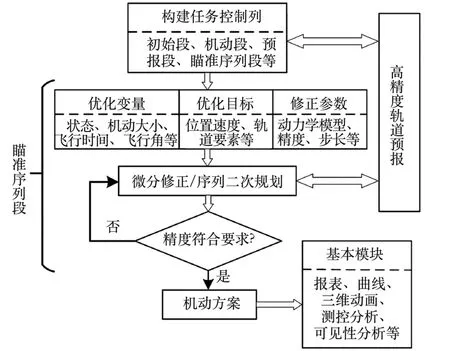
图2 瞄准序列段求解流程图Fig.2 Solution procedure of target sequence
机动规划模块结构如图3 所示。 规划过程中的结果显示界面如图4 所示,包括运行时间、每一个瞄准序列段的变量当前值和误差值等。
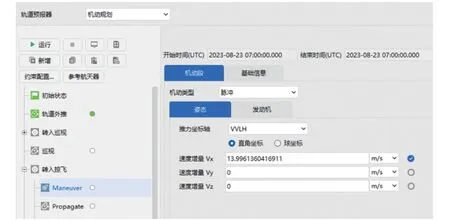
图3 ATK 软件机动规划模块结构Fig.3 Structure of the maneuver planning module of ATK
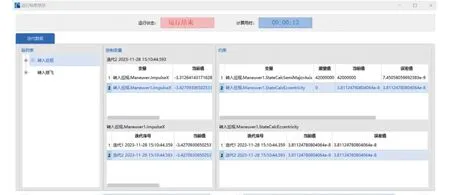
图4 ATK 软件规划收敛结果Fig.4 Solution of the maneuver planning module of ATK
3 受控绕飞任务分析与轨迹规划
3.1 受控绕飞任务流程
航天器受控绕飞任务包括进入绕飞、快速绕飞和退出绕飞3 个阶段[16⁃17]。 进入绕飞段的目的是逐步减小与目标卫星的相对距离,确保达成绕飞条件;快速绕飞段的目的是使服务航天器环绕目标航天器运动以完成相应任务;退出绕飞即逐步扩大与目标卫星的相对距离,退出绕飞任务。由于退出绕飞与进入绕飞流程相似,本文仅分析受控绕飞任务的前2 个阶段。
假设服务航天器采用多脉冲机动方式完成受控绕飞任务。 多脉冲机动轨迹规划的一个关键问题是确定每个脉冲的施加位置,一种可行的方法是在相对运动轨迹上选取若干导航点,把导航点作为脉冲位置,进而将轨迹优化问题转化为关于导航点的参数优化问题[18]。
下面给出基于导航点的受控绕飞轨迹设计与规划方法。
3.2 受控绕飞轨迹设计
3.2.1 进入绕飞段
不考虑姿态跟踪时,进入绕飞段的机动抵近过程属于3-DOF 问题。 在坐标系Sp中,已知服务航天器初始相对位置r0和抵近相对目标点rf,则连接这2 个点的所有曲线均可作为导航点的参考曲线。 为方便起见,本文采用直线抵近策略,即导航点的参考曲线为始末位置点连线。 由于卫星采用脉冲机动方式,因此其实际运动轨迹如图5所示,可将其定义为多脉冲拱线抵近。
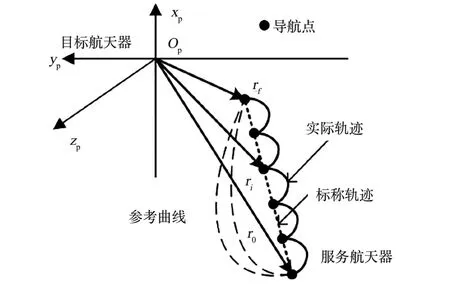
图5 进入绕飞示意图Fig.5 Illustration of entry section
确定机动抵近的参考曲线后,导航点的数量和位置由相邻导航点之间最大转移飞行角Amax和进入绕飞段任务时长Tw决定,计算方法见3.3.1 节。
3.2.2 快速绕飞段
与自然绕飞相比,航天器受控绕飞周期短(通常为目标航天器轨道周期的0.1~0.5 倍[7]),且能够根据需要控制服务航天器按照规划轨迹运行,更具有应用价值。 已有的绕飞构型包括单脉冲“水滴”形、多脉冲受限圆形、“田径场”形、多脉冲“双椭圆”形和多脉冲“双水滴”形等[17,19]。 这些构型的本质区别在于导航点不同,其中多脉冲受限圆形绕飞构型最为复杂且具有普遍性,下面给出简要介绍并基于此设计多脉冲绕飞轨迹。
多脉冲受限圆形绕飞的标称轨迹为圆形。 理论上航天器需采用连续变推力机动才能实现圆形受控绕飞,然而工程中通常应用继电型推力或脉冲推力且允许实际轨迹与标称轨迹有一定偏差。因此为简化问题,可以限定脉冲位置(导航点)在标称轨迹上,采用多脉冲机动实现圆形绕飞。 以图6 所示多脉冲圆形绕飞为例,服务航天器需进行8 次脉冲机动完成对目标航天器的绕飞。
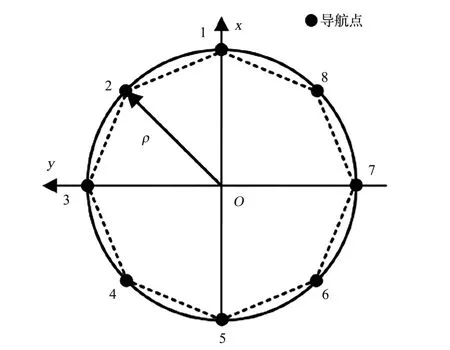
图6 多脉冲圆形绕飞标称轨迹Fig.6 Nominal trajectory of flyaround
对于圆形绕飞构型,圆上导航点数量可任意指定,其在圆上的分布可采用等角等时间法[20]确定,即脉冲位置在标称轨迹上等间隔分布。
3.3 受控绕飞轨迹规划
选定参考轨迹上所有导航点后,可以将受控绕飞任务的全流程轨迹规划问题分解为若干相邻导航点之间的轨迹规划子问题,每个子问题均可通过一个瞄准序列段实现。
如图7 所示,服务航天器在A 点施加一次脉冲机动经过一段时间外推后到达B 点,则从A 点到B 点的轨迹可通过一个瞄准序列段求解得到。根据图2 可知,该瞄准序列段由一个机动段和一个外推段组成,因此其优化变量是机动大小和外推时间,优化目标是B 点的位置(也是终端约束)。
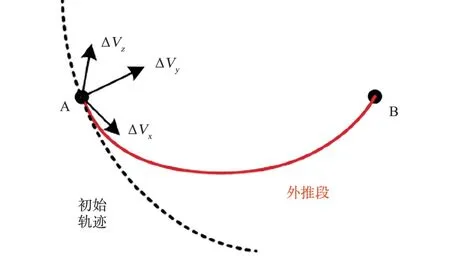
图7 相邻导航点间的轨道转移Fig.7 Orbital transfer between adjacent waypoints
下面给出受控绕飞任务规划时所包含所有瞄准序列段的参数,包括规划变量及初值、外推停止条件和终端约束等。 受控绕飞中所有终端约束均为各段的瞄准点,即为目标航天器LVLH 坐标系中的相对状态。
3.3.1 多脉冲拱线抵近轨迹规划
已知航天器初始相对位置[x0,y0,z0]T,抵近目标相对位置[xw,yw,zw]T通常设为多脉冲圆形绕飞起始位置点。 若给定机动抵近任务时长Tw和相邻导航点之间最大转移飞行角Amax,则能够确定服务航天器进入绕飞段的规划参数。
当目标航天器轨道为近圆轨道(e<0.01)时,拱线抵近段子段数量为Wnum,其大小见式(3)。
其中,Tt为航天器轨道周期,⎿·」 为向下取整符号。 此时,所有段的停止条件均为时间dura⁃tion1,其大小见式(4)。
当目标航天器轨道为椭圆轨道时,需首先计算服务航天器在Tw后真近点角变化量Δf,该过程可参考文献[15]。 进而可得拱线抵近段子段数量Wnum,见式(5)。
此时,前(Wnum-1)段的停止条件为纬度幅角ArgLat1(当轨道倾角为0 时,改用赤经作为停止条件),其大小见式(6)。
第Wnum段的停止条件为时间,即进入绕飞的剩余时间duration2,见式(7)。
其中,Tr为前(Wnum-1)段的飞行时间。
已知拱线抵近段子段的数量,则可以计算出每一段的终端约束,即瞄准序列段的瞄准点[xi,yi,zi]T,见式(8)。
3.3.2 多脉冲圆形绕飞轨迹规划
航天器进行多脉冲圆形绕飞规划时需给定如下6 个参数:
1)绕飞半径Cr。 即标称轨迹圆的半径;
2)绕飞点数Pointnum。 即在一圈标称轨迹上设定的导航点数量;
3)绕飞圈数Revnum;
4)绕飞中心相对目标位置[d0,d0,d0]T;
5)绕飞平面相对目标轨道平面转角[θx,θy,θz] ;
6)绕飞周期时间比例Tratio。 即目标航天器轨道周期与绕飞周期的比值。
绕飞段子段的数量Cnum见式(9)。
其中,「·⏋为向上取整符号。
基于以上参数,可以得到每一段的终端约束,即瞄准点[xci,yci,zci]T,其表达式如式(10)所示。
当目标航天器轨道为近圆轨道(e<0.01)时,Cnum段的停止条件均为时间duration3,其大小见式(12)。
当目标航天器轨道为椭圆轨道时,Cnum段的停止条件均为纬度幅角ArgLat2(当轨道倾角为0时,改用赤经作为停止条件),其大小见式(13)。
4 自主通用软件实现与分析
本节基于ATK 轨道机动规划工具完成对服务航天器多脉冲受控绕飞任务的规划求解。 根据第3 节所述受控绕飞任务轨迹设计和规划方法,软件对相关程序进行封装,并预留了参数设置接口,如图8 所示,用户可根据实际任务需求更改参数。
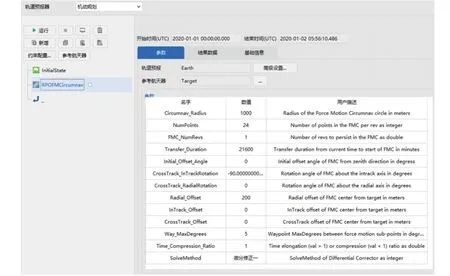
图8 受控绕飞参数输入界面Fig.8 Interface of input parameters in forced fly⁃around section
4.1 受控绕飞规划和实现
由于GEO(Geostationary Orbit)轨道卫星具有轨道高度高、覆盖区域广、星下点轨迹固定等独特的轨道性质,各国在GEO 轨道上部署了通信、导航、预警等昂贵精密的卫星,这些卫星是在轨服务的重点对象。 本节以GEO 轨道航天器作为目标航天器,给出受控绕飞全流程轨迹。
目标卫星轨道根数如表1 所示。 绕飞任务参数如表2 所示。 根据表2 中参数设置情况,基于本文方法可得受控绕飞各段参数如表3 所示。ATK 受控绕飞相对运动轨迹如图9 所示。 其中,洋红色线为目标航天器在惯性系下的绝对运动轨迹;绿色线为服务航天器以目标航天器为中心的相对轨迹。
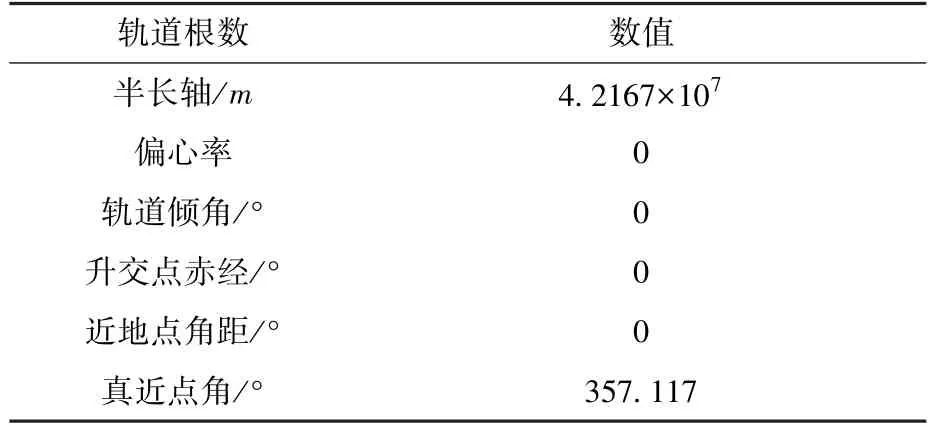
表1 目标卫星轨道根数Table 1 Elements of the target
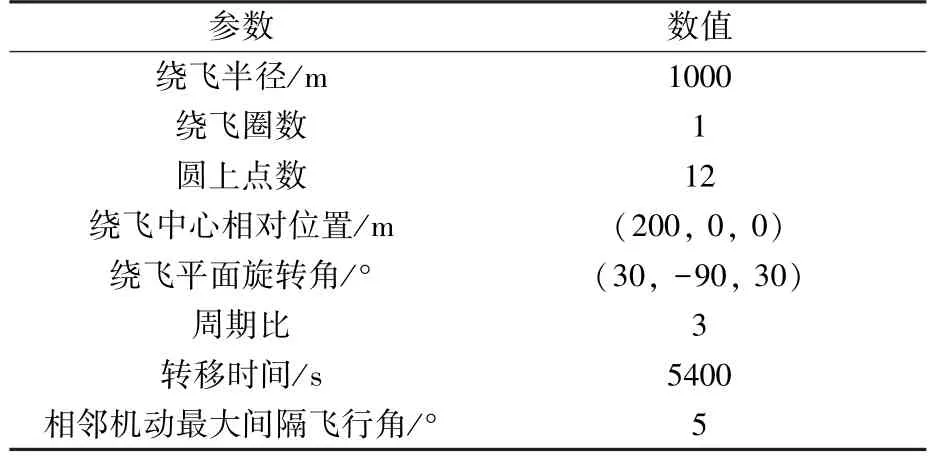
表2 受控绕飞任务参数Table 2 Parameters of forced flyaround mission
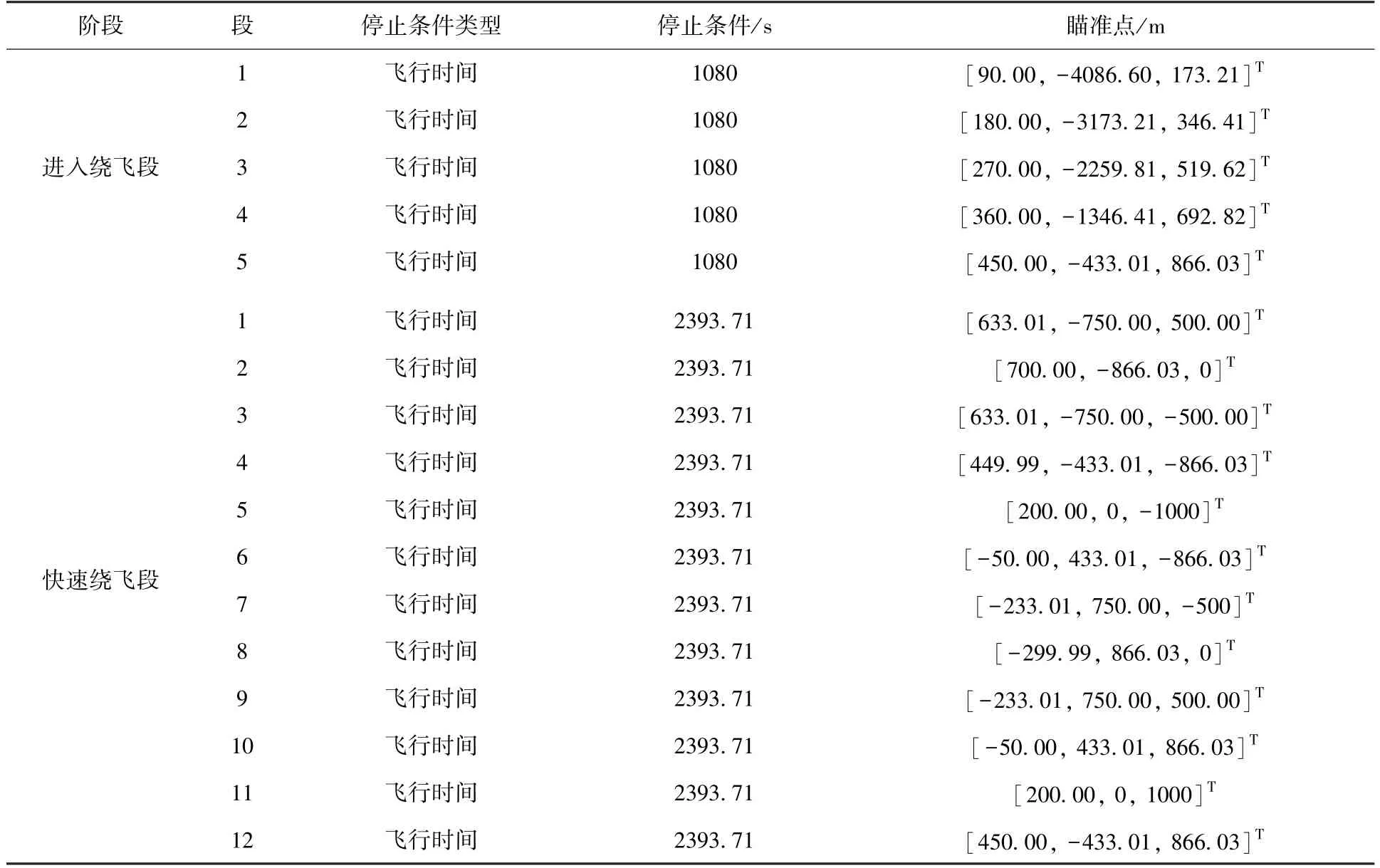
表3 受控绕飞各段参数Table 3 Parameters of all segments in forced flyaround

图9 受控绕飞相对运动轨迹Fig.9 Relative trajectory of forced flyaround
由图9 可知,航天器受控绕飞运动实际轨迹与设计轨迹相符合,ATK 机动规划工具能够实现对受控绕飞任务的规划求解。 为验证软件机动规划求解的正确性和精度,表4 给出了ATK 和STK软件在采用相同的想定和受控绕飞参数的情况下的机动规划结果以及在机动时刻的相对位置信息。 由表4 中相对位置结果可知,STK 和ATK 在各段均能准确到达表3 中瞄准点位置,与设计轨迹相符。
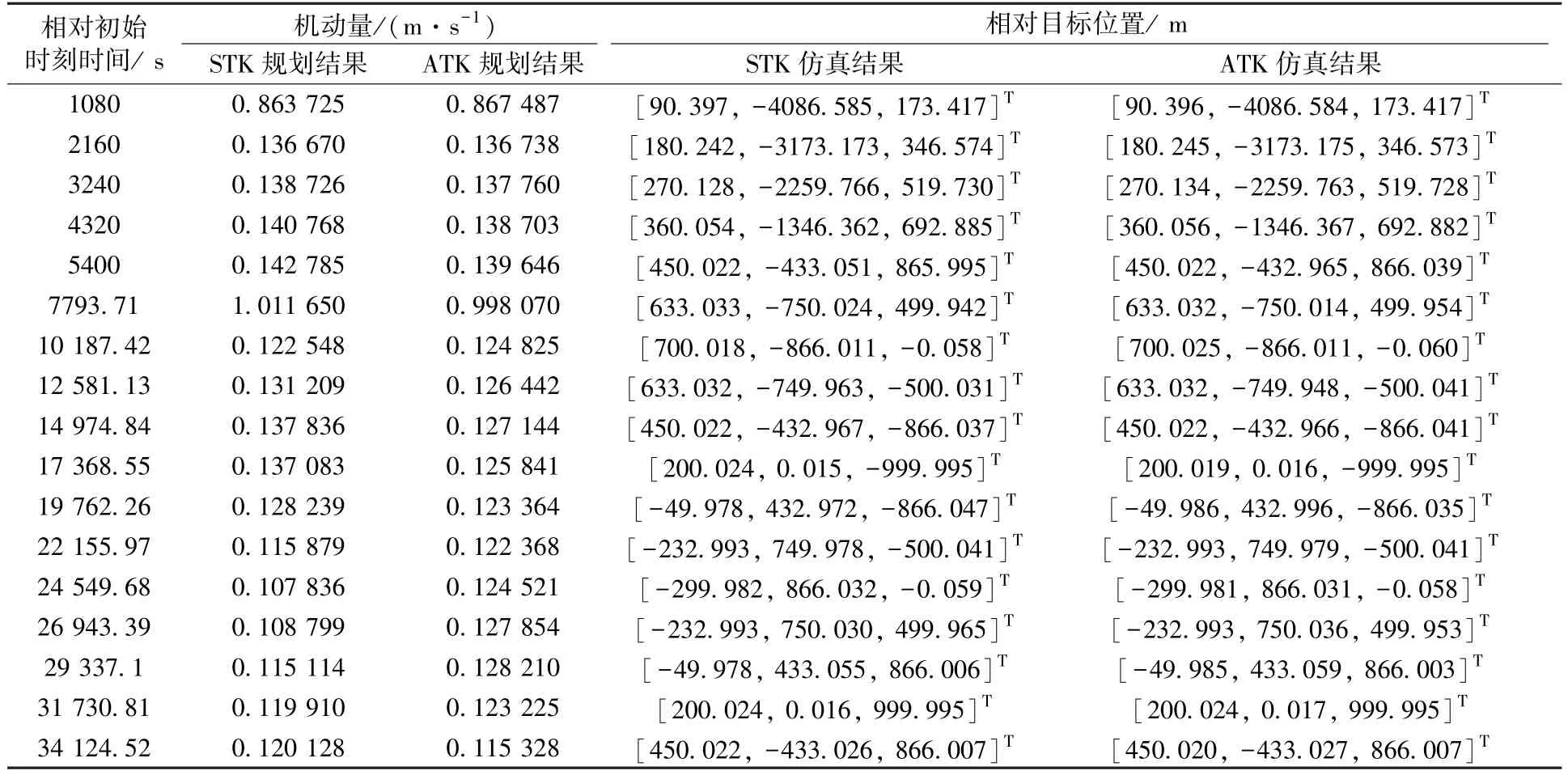
表4 STK 和ATK 计算结果Table 4 Results of all segments in STK and ATK
ATK 规划所得控制序列和STK 对比结果如图10(a)所示,对比可知2 个软件在各导航点规划所得控制量基本一致。 ATK 与STK 中服务航天器相对距离如图10(b)所示,结果表明,两软件位置仿真结果相差不超过0.01 m,满足精度要求。
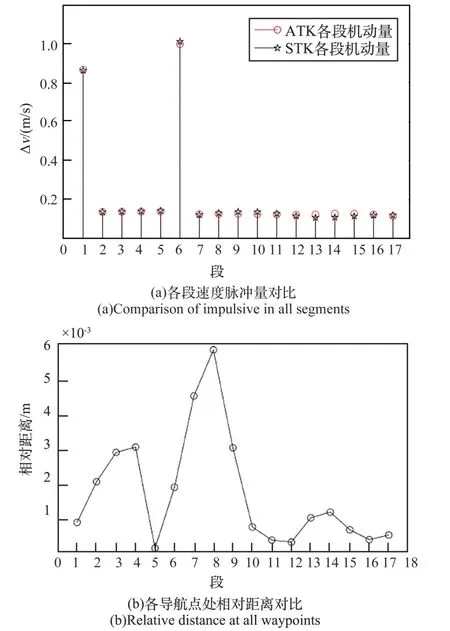
图10 ATK 与STK 对比结果Fig.10 Comparison of STK and ATK
4.2 受控绕飞参数分析
4.2.1 进入绕飞段参数分析
由2.3.1 节可知,在确定进入绕飞段的始末位置后,其运动轨迹由进入绕飞段任务时长Tw和相邻导航点之间最大转移飞行角Amax决定。
Tw和Amax对进入绕飞段脉冲总量的影响如图11 所示。 由图11 (a)可知,总的速度脉冲随着进入绕飞段任务时长的增加而不断减小,并逐渐趋于稳定值。 由图11 (b)可知,增大Amax可减小进入绕飞段的脉冲消耗。
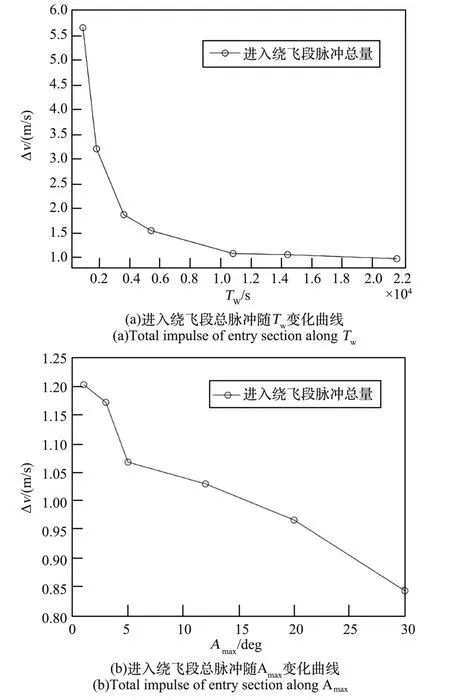
图11 进入绕飞段总脉冲变化情况Fig.11 Changes of total impulse in entry section
4.2.2 快速绕飞段参数分析
快速绕飞段参数有绕飞半径、绕飞点数、绕飞周期时间比例、绕飞圈数、绕飞中心相对目标位置和绕飞平面相对目标轨道平面转角。 其中绕飞半径、绕飞点数能显著改变多脉冲绕飞轨迹的形状和大小,绕飞周期时间比例直接决定绕飞周期,因此本文分别分析这3 个参数对快速绕飞段总的速度脉冲的影响,并同时给出相应情况下进入绕飞段总的速度脉冲。
图12 (a)所示为2 段总的速度脉冲(Δv)随绕飞半径变化的结果。 由于绕飞半径决定了进入绕飞段的终端位置,因此其对进入绕飞段总的速度脉冲有微小的影响。 对于快速绕飞段,其总的速度脉冲随着绕飞半径增大而增大,这是由于半径增大导致单次转移距离变大。
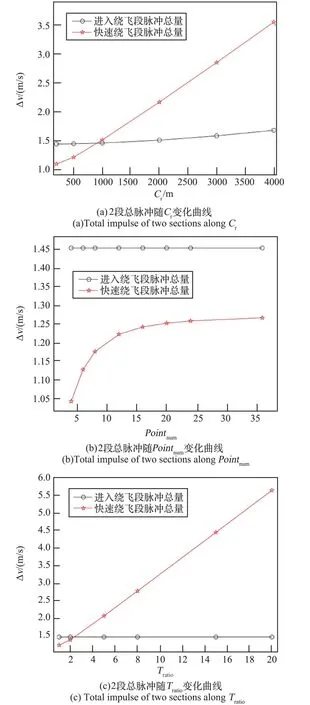
图12 2 段总脉冲变化情况Fig.12 Changes of the total impulse in two sections
图12 (b)所示为2 段总的速度脉冲随绕飞点数的变化结果。 当绕飞点数较少时,快速绕飞段的总速度脉冲随着绕飞点数的增加而增加。 但随着绕飞点数的不断增加,速度脉冲变化量逐渐减小,总的速度脉冲逐渐趋于稳定值。 实际上,当绕飞点数较大时,绕飞段的实际轨迹逐渐逼近标称圆轨迹,且相邻2 个导航点之间的距离及转移时间均不断减小,此时的多脉冲机动趋于连续变推力机动,因此其所需速度脉冲逐渐趋于稳定值。此外,由图12 (b)可知,绕飞点数不会对进入绕飞段的机动产生影响。
图12 (c)为2 段总的速度脉冲随绕飞周期时间比例变化的结果。 随着Tratio的增大,绕飞周期不断减小,导致相邻导航点之间的转移时间减小,因此所需速度增量逐渐增大。 此外,快速绕飞段的周期不会对进入绕飞段的机动产生影响。
5 结论
基于自主航天任务设计工具箱建立了航天器受控绕飞的轨迹设计及规划方法。 设计了进入绕飞段和快速绕飞段的轨迹,针对目标航天器轨道为圆轨道和非圆轨道的情况,分别给出了多脉冲拱线抵近和多脉冲圆形绕飞的规划方案,并通过ATK 实现了受控绕飞任务的轨迹规划。 通过参数分析可知,受控绕飞所需总的速度脉冲随进入绕飞段的任务时间和最大转移飞行角的增大而减小,随快速绕飞段绕飞半径、绕飞点数、绕飞周期时间比例的增加而增加,在设计绕飞构型时需要综合权衡,在不影响任务效果的前提下,应尽量减少机动次数以节省燃料。

