不同操纵方式对十字伞滑翔性能的影响研究

黄云尧， 武士轻， 张 扬，3

（1.南京航空航天大学航天学院， 南京 210016； 2.北京空间机电研究所， 北京 100094；3.中国航天科技集团有限公司航天进入、减速与着陆技术实验室， 北京 100094）

1 引言

近年来，随着精确制导及控制技术的发展，基于十字伞等传统降落伞的精确空投技术也逐渐引起国内外研究人员的关注。 十字伞具有低成本、高可靠性、工艺简单、稳定性好、开伞动载小等优点。 十字伞系统因其低滑翔比特性使其在受限区域内更容易实现精确空投，低成本这一优势也使其在大规模、低附加值物资空投方面备受关注。

十字伞的常用操纵方式一般可分为2 种，一种针对伞绳，即通过操纵伞绳使伞衣产生非对称变形，从而获得一定的滑翔能力，这是目前最为常见的操纵方法。 Fields 等［1］通过单个执行器对十字伞的某根伞绳长度进行调整，达到对十字伞自旋速率进行控制的目的。 Gregory 等［2］提出将十字伞的伞臂绑在一起，通过单独的控制线控制角的开启，使相邻十字伞伞臂间的空气得以流通，使十字伞发生平移，从而控制十字伞的飞行方向。Gao 等［3］利用数值手段模拟了十字伞的开伞过程，通过对2 组伞绳长度进行动态调整，分析十字伞在不同操纵条件下的充气性能。 另一种操纵方式针对伞衣，通过改变伞衣几何形状，开窗、加装排气扰流板等方式改变十字伞的几何透气性。Fagley 等［4］通过加装排气扰流板的方式对十字伞进行优化设计，通过改变开启角度达到改变十字伞滑翔特性的目的。 Potvin 等［5］在1000～2000 英尺的高空飞行试验中对比分析了标准型十字伞和混合型十字伞的可操纵性。 Herrington 等［6⁃7］利用风洞试验比较了5 种不同形状的十字伞的滑翔特性和落点精度。

十字伞的充气过程变形大、时间短，在开伞的过程中容易受到伞衣初始状态、透气性等参数的影响，周围流场的变化也会对其产生较大的影响，属于流固耦合的范畴。 LS⁃DYNA 软件因其特有的流固耦合算法而适用于降落伞充气过程的模拟，其中ALE（Arbitrary Lagrange⁃Euler）算法更是被广泛应用于十字伞开伞过程的模拟［8⁃10］。 S⁃ALE （Structured ALE） 算法则是在传统ALE 算法的基础上进一步优化，通过关键字设置自动生成结构化网格，大大减少了计算时间和内存开销，相较于ALE 算法更为简单高效，近年来在降落伞的流固耦合模拟中也得到了较为成功的应用［11⁃14］。

总的来说，国内外针对十字伞的可操纵性能主要通过风洞试验和飞行试验来进行，相关的仿真研究较为罕见，因此对其展开可操纵性能研究，研究操纵方式对十字伞滑翔性能的影响对于拓展十字伞的应用范围具有十分重要的意义。 本文将利用LS⁃DYNA 软件中的S⁃ALE 求解器，模拟分析角空气喷口和加装排气扰流板这2 种不同的操纵方式对十字伞滑翔性能的影响，以期为基于传统伞的精确空投系统的研制提供一定的参考意见。

2 数值方法

S⁃ALE 方法与ALE 方法的理论完全一致，但与ALE 方法中直接导入网格模型不同的是，S⁃ALE 流场域只需要通过关键字∗ALE＿STRUC⁃TURED＿CONTROL＿POINTS 控制流场在三维方向上的位置和网格数量；通过∗ALE＿STRUCTURED＿MESH 创建网格；最后通过INITIAL＿VOLUME＿FRACTION＿GEOMETRY 关键字对流场区域进行物质材料（空气）填充即可。 由程序本身自行创建网格，从而省去创建网格—程序读入过程中由于模型单元个数过大引起的文件输入输出时间过长的问题，在理论和算法相同的情况下，利用结构网格节点排序的规律性对ALE 算法进行简化，通过关键字控制自动生成结构化网格，大大减少了计算时间和内存开销。

采用S⁃ALE 方法进行流固耦合模拟。 流场控制方程由质量方程、动量方程和能量方程组成［15］，分别为公式（1）～（3）。

式中，ρ为流体密度；vi为i方向的物体速度，则i方向相对速度wi＝vi－ui；ui为网格速度；bi为单位体积力；xj为j方向欧拉坐标；σij＝－pδij＋μ（vi，j＋vj，i） ，表示应力张量，其中p为压强，μ为动态黏性系数，δij表示Kroneckerδ函数，vj，i＝∂vj／ ∂vi；divσij表示流体应力张量的散度， divσij＝∂σij／ ∂xj；E为能量。

网格控制方程为公式（4）。

式中：f（Xi，t） 表示物体在方向拉格朗日坐标下的位移；f（xi，t）表示物体在i方向欧拉坐标下的位移；Xi表示i方向拉格朗日坐标；xi表示i方向欧拉坐标；wi为i方向相对速度；t表示时间。

十字伞结构的控制方程如公式（5）所示［16］。

式中：M，C，K分别表示单元质量、阻尼模量和弹性模量；F表示单元所受合力；w为相对速度。

3 计算模型与操纵方式设置

在风洞或飞行试验中，对十字伞的操纵通常发生在十字伞稳定成型后。 数值仿真中，如何得到稳定成型的十字伞，并以此为基准伞型施加相应的操纵方式是其中的关键问题。 本文将采用S⁃ALE（Structured ALE）方法计算得到稳定成型的十字伞，在此基础上模拟分析角空气喷口仿真与加装排气扰流板这2 种不同的操纵方式对十字伞滑翔性能的影响。

3.1 计算模型

本文采用长宽比为3 ∶1 的十字伞模型作为基准伞型，伞衣长度为6 m，宽度为2 m，面积为20 m2。 伞衣由二阶壳单元离散，伞衣材料通过关键字∗MAT＿FABRIC 设置，密度为74 kg／m3，弹性模量为0.064 GPa，厚度为2.5×10－3m。 伞绳由二阶梁单元离散，伞绳材料通过关键字∗MAT＿CABLE ＿ DISCRETE ＿ BEAM 设 置， 密 度 为623 kg／m3，弹性模量为10.9 GPa。 伞绳截面为圆截面，截面面积为7.0686×10－6m2，收口绳材料属性与伞绳一致。

由于采用SALE 方法，流体背景网格与十字伞固体网格可以相互独立存在。 为了控制流场域计算网格的规模，对伞衣周围的流场网格进行局部加密，加密区域网格尺寸与伞衣表面网格尺寸相同（均为0.1 m），加密区域外至远场区域网格尺度逐渐稀疏。 流场填充材料为空气，通过关键字∗BOUNDARY＿PRESCRIBED＿MOTION＿SET 在入口处施加20 m／s 的恒定来流速度。 十字伞周围的流场网格剖面图如图1 所示。 流固耦合算法通过关键字∗CONSTRANT＿LAGRANGE＿IN＿SOLID 设置，选取其中的适合织物类仿真的ctype11 算法。

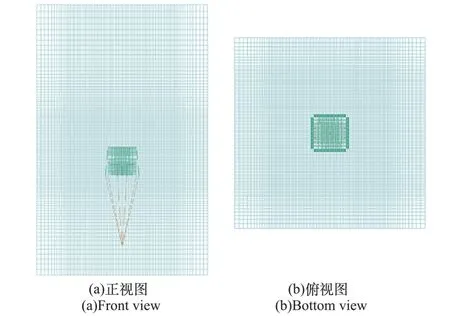
图1 十字伞周围的流场网格剖面图Fig.1 Computation mesh of the fluid domain

数值模拟中，需要在伞衣稳定成型后，以此为基准状态施加相应的操纵方式，从而保证数值稳定性。 具体思路为：首先建立如图2 所示的初始伞型，采用S⁃ALE 方法得到充气稳定后的伞型。将稳定成型的十字伞模型导出，在此基础上研究施加不同操纵方式对十字伞滑翔性能的影响。

图2 十字伞初始伞型Fig.2 Initial geometry of the cruciform parachute

图3 展示了未施加约束的十字伞成型情况，可以看到伞衣未能完全展开，成型效果较差且存在严重的坍缩现象，这将对后续的操纵效果产生影响。 为此，本文参照文献［4］所述方法对十字伞施加初始约束，采用关键字∗BOUNDARY＿SPC＿SET＿BIRTH＿DEATH 对十字伞模型施加局部约束，使伞衣在前0.5 s 保持形状不变的同时使流场得到充分发展。

图3 未施加约束的十字伞成型图Fig.3 Computed shape of the cruciform parachute without constraint

将经上述前处理方法约束后的十字伞模型导入LS⁃DYNA，采用SALE 求解器计算得到如图4 所示稳定成型后的十字伞形状。 与图3 所示未施加约束的伞型相比，施加约束后十字伞的成型较好，无明显的坍缩现象。 后续将以此为基准伞型，分别模拟角空气喷口和加装排气扰流板的操纵过程。

图4 施加约束后的十字伞成型图Fig.4 Computed shape of the cruciform parachute with constraint

3.2 角空气喷口设置

角空气喷口通过对基准十字伞的某一组相邻伞臂间的收口伞绳长度进行调整，达到在不影响十字伞自旋行为的前提下，操纵十字伞滑翔的目的。 角空气喷口的原理如图5 所示［4］，十字伞的4 个伞臂分别由收口绳A、B、C、D 绑在一起，通过对其中的一组收口绳C 进行长度的调整，产生一个较大的通风口，使相邻十字伞臂之间的通气量增大，从而产生使十字伞沿C⁃A 方向平移的力，达到操纵十字伞飞行姿态的目的。

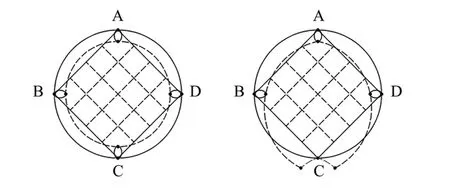
图5 角空气喷口原理图［4］Fig.5 Schematic of the air⁃venting corner［4］

3.3 排气扰流板设置

排气扰流板是在基准十字伞的某一伞臂上加装一个排气扰流板，通过对排气扰流板进行一定程度的操纵使其与伞衣形成不同的偏转角，使更多的气流从排气扰流板开口处流出，产生压力差来改变十字伞的侧向力，从而达到操纵十字伞滑翔的目的。 数值模拟中排气扰流板的大小参考文献［6］中的参数设置。 由于排气扰流板在模拟过程中的形变较小，可以忽略不计，故设置为刚性材料。 排气扰流板的位置及形状如图6 所示。

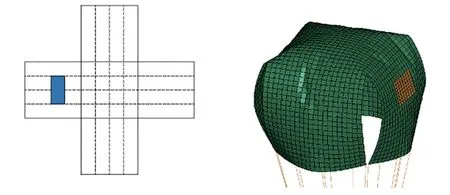
图6 排气扰流板位置示意图Fig.6 Schematic of the bleed air spoiler

在计算设置中，排气扰流板的上边缘与伞衣之间通过铰链连接，下边缘通过连接绳与伞衣相连，通过执行器操纵改变连接绳的长度，从而有效地改变排气扰流板的偏转程度。 通过共节点约束扰流板上边缘与伞衣，随后建立扰流板下边缘与伞衣连接，通过改变连接绳的长度使排气扰流板与伞衣间形成不同的偏转角。

综上所述，采用数值模拟方法研究不同操纵方式对十字伞滑翔性能影响的具体技术路线如图7 所示。

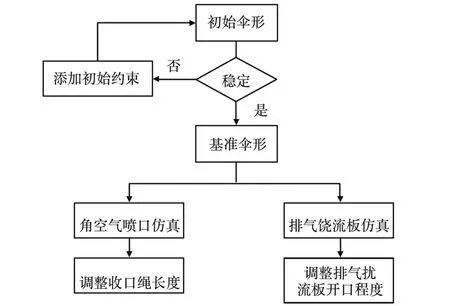
图7 技术路线图Fig.7 Overall workflow

4 结果与分析

4.1 角空气喷口仿真结果

针对角空气喷口，共进行了4 组不同程度的开口程度模拟，即调整收口绳长度使每一组的开口程度分别为0%、33%、66%、100%（其中100%为完全开口，即收口绳C 对于相邻两伞臂之间的约束为0）。 比较这4 组的俯仰角和航向角变化，其中俯仰角和航向角分别用于表征十字伞的滑翔和自旋特性。

2 s 时计算得到的4 组不同开口程度的十字伞伞型，如图8 所示。 从图中可以看到，不同开口程度均能得到稳定的伞型。 此外，从俯视图中可以看出，相较于基准伞型（开口程度为0），伞绳的交汇点相较于十字伞的中心点有一定程度的偏转，说明十字伞产生了一定程度的滑翔。

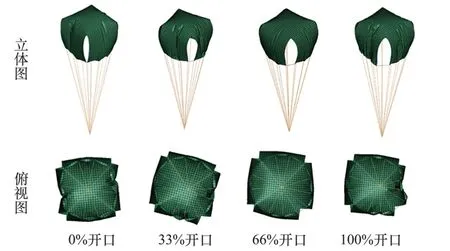
图8 不同开口程度的十字伞立体图及俯视图Fig.8 Isometric view and bottom view of the cruci⁃form parachute with different stroke exten⁃sion

图9 显示了4 组伞型的俯仰角变化趋势，可以看到，基准伞型的俯仰角变化较小，进行开口操作后，俯仰角均有不同程度的增加，1.8 s 后伞型变化逐渐趋稳，未施加操纵的基准伞型俯仰角为0.25°完全开口的十字伞伞型俯仰角为2°，十字伞的俯仰角有较为显著地提升，十字伞有明显的滑翔趋势。

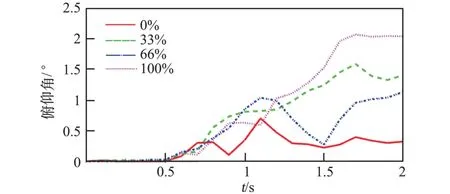
图9 不同开口程度的十字伞俯仰角变化Fig.9 Pitching angle of the cruciform parachute with different stroke extension

图10 显示了4 组伞型的航向角变化趋势，可以看到，各组伞型都在以相似的方向旋转，且随着开口程度的变化，航向角也有一定的变化，表明角空气喷口操控操作具备一定的操控十字伞自旋行为的能力。

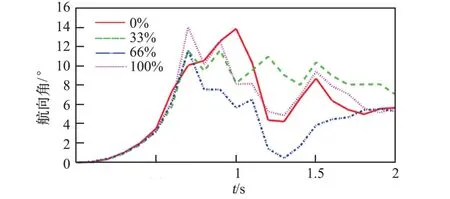
图10 不同开口程度的十字伞航向角变化Fig.10 Heading angle of the cruciform parachute with different stroke extension

为了分析滑翔行为产生的机理，针对不同开口程度，选取不同时刻伞衣周围的速度云图，如图11 所示。 与未进行开口操作的基准伞型相比，其他3 组伞型在开口处的气流速度明显增大，左上角未开口处的气流和右下角开口处的气流速度有着较为明显的差异，且随着开口幅度的增加，通过开口处速度较大的气流量越多，从而在图5 所示的A、C 之间产生较大压力差，导致十字伞的俯仰角增大，产生滑翔的趋势。

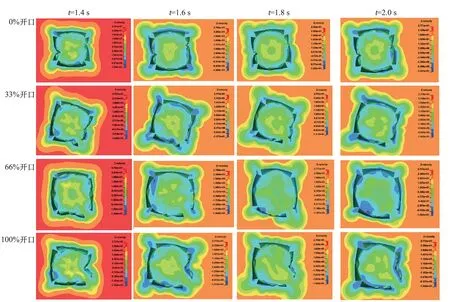
图11 不同开口程度的十字伞不同时刻速度云图Fig.11 Velocity contours with different stroke extension at different time instants

仿真结果表明，不同的角空气喷口开口程度对十字伞的俯仰角变化影响较大，能够较大地增加十字伞的俯仰角，提高十字伞的滑翔性能，从而具备一定的操纵能力，同时角空气开口也具备一定的调节十字伞自旋行为的能力。

4.2 排气扰流板仿真结果

针对排气扰流板，共进行了4 组不同偏转程度模拟，即将排气扰流板进行不同角度（0°、10°、20°、30°）的偏转，比较了4 组伞型的轴向力和侧向力变化，轴向力和侧向力变化分别用于分析对十字伞的阻力系数和滑翔性能影响。

2 s 时计算得到的4 组不同偏转角度的十字伞伞型如图12 所示。 4 组伞型的轴向力、侧向力变化趋势如图13、14 所示。

图12 不同偏转角度排气扰流板立体图及俯视图Fig.12 Isometric view and bottom view of the cruci⁃form parachute with different deflection an⁃gle of the bleed air spoiler

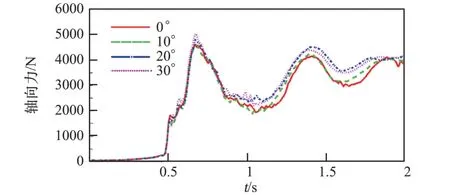
图13 不同偏转角度排气扰流板轴向力图Fig.13 Drag force of the cruciform parachute with different deflection angle of the bleed air spoiler

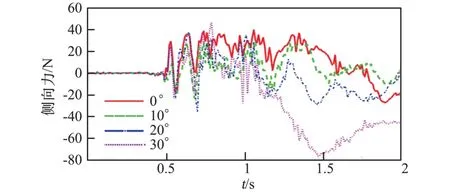
图14 不同偏转角度的排气扰流板侧向力图Fig.14 Lateral force of the cruciform parachute with different deflection angle of the bleed air spoiler

1）在0～0.5 s 时，伞衣和空气刚开始接触，气流与排气扰流板接触尚不充分，各组伞型的轴向力和侧向力变化较小。

2）0.5～1 s 时，十字伞逐渐成型，轴向力开始大幅度增加，侧向力也发生较大变化。

3）1～1.5 s 时，此阶段十字伞趋于稳定，扰流板完全打开，十字伞的侧向力增大，各组伞型的侧向力表现出较大的差异，且随着排气扰流板偏转角度的增大，侧向力的大小也随之增大。 相较于各组伞型的侧向力差异，轴向力虽然在此阶段有较大的变化，但各组伞型的轴向力的大小及变化趋势相差较小。

4）1.5～2.0 s 时，此阶段十字伞基本稳定，轴向力和侧向力的变化趋于平缓，不同伞型的轴向力差异较小，且各组伞型达到稳定时的充气时间也基本一致。 而侧向力差异较大，相较于基础伞型，加装排气扰流板的伞型侧向力增加较为明显，在偏转角为30°时，增幅最大，侧向力最大为47.3 N。

为了研究排气扰流板产生侧向力的机理，选取扰流板偏转角度为20°的伞型4 个不同时刻的速度云图，如图15 所示。 可以看到，气流在十字伞的前缘开始分离，十字伞的两侧有明显的涡流，且涡流逐渐聚集到十字伞右侧（排气扰流板一侧），十字伞的两侧产生压力差使十字伞的侧向力显著增加，呈向左侧滑翔的趋势。

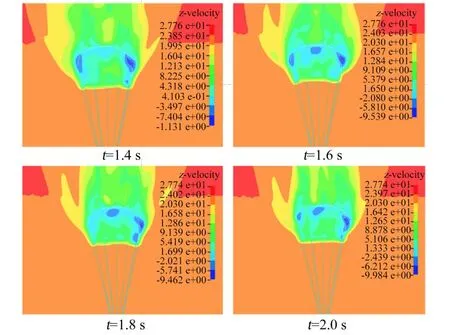
图15 扰流板偏转角为20°的十字伞四个时刻速度云图Fig.15 Velocity contours of the cruciform parachute with 20°deflection angle of the bleed air spoi⁃ler at different time instants

仿真结果表明，排气扰流板对十字伞的侧向力影响较大，但对十字伞的轴向力影响较小，因此，排气扰流板偏转操纵操作可以在不影响十字伞的阻力性能的前提下，具有一定程度操纵十字伞滑翔的能力。

5 结论

本文采用数值模拟的手段，研究了角空气喷口和加装排气扰流板2 种操纵方式对十字伞滑翔性能的影响。 数值结果表明，2 种操纵方式均可对十字伞的滑翔性能产生较大的影响。

1）通过收口绳对十字伞伞衣进行角空气开口操作，可以增加十字伞的俯仰角，在开口达到100%时，俯仰角最大，为2°；通过偏转排气扰流板，以提升侧向力，侧向力随着偏转角度增大逐渐提升，在30°时达到最大，为43.7 N。 2 种操纵方式均能使十字伞具备一定的滑翔能力。

2）不同的角空气喷口开口程度对十字伞的俯仰角变化影响较大，能够较大地增加十字伞的俯仰角，提高十字伞的滑翔性能，从而具备一定的操纵能力，同时角空气开口也具备一定的调节十字伞自旋行为的能力。

3）排气扰流板偏转操作对十字伞的侧向力影响较大，但对十字伞的轴向力影响较小，因此，排气扰流板偏转操纵操作可以在不影响十字伞的阻力性能的前提下，具有一定程度操纵十字伞滑翔的能力。

本文的研究丰富了十字伞精确空投系统的操纵方式，对基于传统伞的精确空投系统的研制具有一定的参考意义。 后续可以与风场预测方法以及轨迹导航策略相结合，模拟更加真实场景下的精确空投过程。