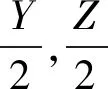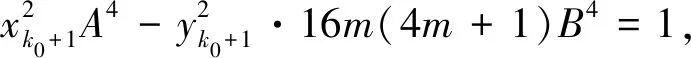关于Pell方程组X2-m(4m+1)Y2=1和Y2-bZ2=16的解数
闫档档,杨海,陈江涛
(西安工程大学理学院, 陕西 西安 710048)
0 引言及结论
设Z,Z+分别是全体整数和全体正整数的集合,a,b是不同的正整数。近年来,关于Pell方程组
x2-ay2=k,y2-bz2=l,(k,l∈Z+)
解的研究已有一些成果:当(k,l)=(1,1)时,Arwin[1]初步研究了方程组的可能性;Ljunggren[2]证明了当(a,b)=(2,3)时,方程组仅有解(x,y,z)=(3,2,1);Mohanty和Ramasamy[3]考虑了(a,b)=(2,20)的情形;Baker和Davenport[4]运用Baker关于对数线性型的下界估计,给出了对于确定的正整数对(a,b)求解方程组的方法;设N(a,b)表示方程组正整数解的个数,Bennett[5]证明了N(a,b)≤3;Cipu和Mignotte M[6]改进了Bennett[5]的结果,证明了N(a,|b)≤2;Yuan[7]证明了当a>3.31×1035时,N(a,b)≤2;Yuan[8]证明了当a=4m(m+1)时,N(a,b)≤1;He[9]改进了Bennett[5]和Yuan[7]的结论,证明了N(a,b)≤2。当(k,l)=(1,16)时,万飞和杜先存[10]证明了当a=5时,方程组的正整数解只有(x,y,z)=(2 889,1 292,72);瞿云云[11]证明了当a=18时,方程组的正整数解只有(x,y,z)=(1 960 1,4 620,136)。本研究主要讨论当a=m(4m+1),b=2p或2pq(p,q为互异的奇素数)时,Pell方程组X2-m(4m+|1)Y2=1和Y2-bZ2=16的正整数解数。
定理如果m和b为正整数,且a=m(4m+1),b=2p或2pq(p,q为互异的奇素数),那么Pell方程组
X2-aY2=1,Y2-bZ2=16
(1)
至多有一组正整数解(X,Y,Z)。
1 关键性引理
设a,b是不同的正整数,且a,b都不是完全平方数。令α和β分别是x2-ay2=1和y2-bz2=1的基本解。记
(2)
引理1[12]1)若d=gcd(m,n),则gcd(Um,Un)=Ud;
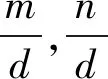

4)若Um≠1,Um|Un当且仅当m|n;

6)U2m=2UmVm。
引理2[13]设k0,k1,k2,q均为正整数,且k2=2qk1±k0,0≤k0≤k1,那么:
1)Uk2≡±Uk0(bmodUk);
2)若2|q,则Vk2≡Vk0(bmodVk1);
3)若2 |/q,则Vk2≡-Vk0(bmodVk1)。
设(x,y,z)是
x2-ay2=1和y2-bz2=1
(3)
的正整数解,那么存在正整数k,l使得
(4)
用N(a,b)表示(3)式的正整数解(x,y,z)的个数,设(x0,y0,z0)是(3)式的正整数解且对应的y值最小,k0,l0对应(4)式中的k,l,即
(5)


k0|k⟹y0|y⟹l0|l
(6)

k=2qk0±s,0 (7) 由(7)式和引理2可知 y=Uk≡±Us(bmodUk0)≡±Us(bmody0), y=V′l≡±V′t(bmodV′l0)≡±V′t(bmody0). (8) (9) 显然有 Uk=xkyk,其中2 |/k;Uk=2xkyk,其中2|k (10) =Uk+1Uk-1,从而由(10)式可得引理4。 引理51)若k为偶数,则xk+1,yk+1,xk-1,yk-1是两两互素得; 2)若k为奇数,则gcd(xk+1,xk-1)=1,gcd(yk+1,yk-1)=1; 3)若k≡1(mod 4),则gcd(xk+1,yk-1)=8m+1,gcd(yk+1,xk-1)=1;若k≡3(mod 4),则gcd(xk+1,yk-1)=1,gcd(yk+1,xk-1)=8m+1。 引理5的证明1)可参见Yuan[14]的定理1;2)和3)可由(9)式,引理1的3)和y2=V1=8m+1可得。 引理6[15]对于任意的正整数A和B,丢番图方程Ax2-By4=1至多有一组正整数解(x,y)。 引理7若k>2,则Uk有一个本原素因子p,此外p|Un当且仅当k|n。 x2-16m(4m+1)y2=1,y2-bz2=1 (11) 情形1若2|k0,则由引理4的2)可得 (12) 和 (13) 若k0>3,则由引理7可知,Uk0+1和Uk0-1分别有本原素因子p和q,结合z0|z、(12)式、(13)式和引理7可知 k0+1|k+1或k-1,k0-1|k+1或k-1 (14) 若k0=2,由引理7可知,U3有一个本原素因子p,由k0-1=1、z0|z、(12)式、(13)式和引理7可知,(14)式也成立。由于k0和k均为偶数,根据引理5的(1)可知xk0+1、yk0+1、xk0-1和yk0-1两两互素;同理,xk+1、yk+1、xk-1和yk-1两两互素。因此,如果k0+1|k+1,k0-1|k-1,那么由(12)式、(13)式、引理1和引理5的1)可知 (15) 其中A,B,C,D均为正整数。由于k0=2,则2 |/(k0+1)(k0-1)(k+1)(k-1),由(8)式和(15)式可得 (16) 和 (17) 情形2若2 |/k。则由引理4的(1)可得 (18) 和 (19) 若k0>3,则由引理7可知,Uk0+1和Uk0-1分别有本原素因子p和q,结合z0|z、(18)式、(19)式和引理7可得 k0+1|k+1或k-1,k0-1|k+1或k-1 (20) 若k0≤3,由于z0>0,因此k0=3。由引理7可知,U4有一个本原素因子p,则k0-1=2。由z0|z、(18)式、(19)式和引理7可知,(20)式也成立。 首先,假设k0+1|k+1,k0-1|k-1。如果2||k0+1,由(9)式和引理1可知 然后,假设k0+1|k+1和k0-1|k+1,那么Uk0+1|Uk+1,Uk0-1|Uk+1。由(2)式可得U2=2(8m+1),由引理1的1)和6)可知gcd(Uk0+1,Uk0-1)=2(8m+1),再由(10)式可知Uk-1=2xk-1yk-1=2(8m+1)□,而由引理5可知,(8m+1)|xk+1和(xk-1,yk-1)=1,因此对于某些正整数有xk-1=A2,yk-1=B2,根据xk-1和yk-1的定义可知(8m+1)2A4-16m(4m+1)B4=1,由引理6和(8m+1)2-16m(4m+1)=1可知,A=B=1或k=2,此时2|k0,与2 |/k0矛盾,故这种情况也是不可能的。同理k0+1|k-1和k0-1|k-1的情况也是不可能的。 综上所述,方程组(11)至多有一组正整数解(x,y,z),从而方程组(1)至多有一组正整数解(X,Y,Z),定理得证。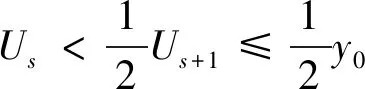
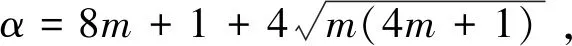
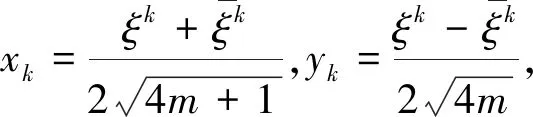

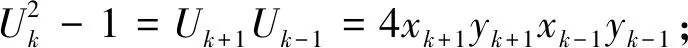



2 定理的证明