铝合金平面薄壁件动态特性研究与建模*

刘 潇,姜颢天,詹奇云,张丹丹,王光余

(1.天津职业技术师范大学,天津 300322; 2.天津市高速切削与精密加工重点实验室,天津 300222)

0 引 言

铝合金薄壁件因其质量轻、结构变化灵活、可加工性能良好等诸多优点,被广泛应用于航空航天、国防等工业制造领域[1-2]。然而,由于其刚性弱,在加工过程中易产生明显的振动现象,严重时还会发生共振。因而在薄壁件的加工中常常伴随着刀具易损坏、工件质量差、工件加工效率低等问题[3]。因此,对薄壁件切削过程中不同加工点开展动态特性实验研究和动态特性模型构建,对提升我国航空航天薄壁装备高效高精制造水平具有重要的理论价值与现实意义。

Zatarain等[4]研究了通过主轴转速连续变化(CSSV)降低铣削振动的方法,研究结果表明,CSSV法的最佳应用情况是高阶瓣的颤振振动,对于低阶瓣则选取恒定转速更为合适。Huang等[5]针对传统稳定性分析模型忽略了不确定因素影响的问题,提出了一种考虑不确定因素的铣削加工动态稳定性概率分析方法。Hamann和Eberlard[6]提出了一种通过观察铣削加工材料去除和激励点变化来系统选择加工参数的方法,该研究采用参数模型降阶法进行稳定性分析。Kiss等[7]基于操作冲击试验产生的瞬态振动提出了一种利用Floquet乘子的模量估计稳定波瓣图的改进预测方法,该方法是一种直接从振动测量中识别切削加工稳定性边界的新方法。Deng等[8]提出了一种铣削颤振稳定性预测模型,并用二阶四矩法计算给定加工参数的可靠性,通过稳定性叶瓣图可以获得更可靠、更精确的稳定区域。Dong等[9]提出了表面法向再生效应,研究发现,弱刚性零件端铣的稳定性与切削速度、进给速度和铣削宽度有关,而与轴向铣削深度无关。

上述关于薄壁件动态特性的研究通常认为,在加工路径上,薄壁件的动态特性是恒定不变的,但是实际工件在加工过程中由于不同的装夹方式、自身材料影响等因素,工件上各点的动态特性是不同的。基于上述问题,笔者对三种不同的典型铝合金材料展开研究,通过锤击实验获得测试点模态参数,分析随着切削路径变化的不同铝合金材料的平面薄壁件动态特性的变化规律,并根据所得到的模态参数,对工件在整体切削路径上的模态参数进行预测。该研究是薄壁件切削稳定性预测研究的重要基础。

1 薄壁件锤击实验

1.1 实验工件

为了较为全面地评估铝合金材料薄壁构件的动态特性,文章选用了三种常见的铝合金材料,分别为6 061、7 050和7 075铝合金。薄板类型选用悬臂立板T形结构。试制了相同尺寸的三种材料试验件,悬臂外形尺寸均为:150 mm×60 mm×3 mm。工件具体参数如表1所列。

表1 铝合金工件参数

1.2 实验方案

在薄壁件铣削过程中,随着切削位置的变化,工件的切削稳定性也随之变化;在切削路径的切入、中间、切出等不同加工位置处,工件由于刚度差异而产生不同程度的变形。为了全面把握薄壁件受切削力作用而发生变形和振动的特征,需要考虑切削路径点变化并开展动态特性试验。

将工件等距分为9个等间距测试点,每相邻的两个测试点距离为18.75 mm。由于所选用的薄壁件均为对称结构,且薄壁件采用完全固支的装夹方式,所以以工件中线为对称轴,工件两侧上对称两点的模态参数相同,远离固定边的两端变形最大且工件中间位置二阶模态振型为零[10]。为了验证模态参数随着工件中轴线的对称性,对件Ⅰ进行全部点的锤击实验,如图1(a)所示。为了避免实验过程中因无法精确控制锤击力度和锤击位置所导致的误差,对其它测试工件选取每个薄壁件的五点进行锤击,如图1(b)所示。

图1 锤击实验锤击点

此次实验采用单点激励单点响应的方式进行,即每次锤击点与测试点为同一点。进行锤击实验时,使用螺栓通过四个通孔将工件固定在测力仪上,并将测力仪与实验平台使用压板完全固定,以尽量减小实验误差;其次通过石蜡依次将加速度传感器粘贴在薄壁件测试点上,并使用力锤锤击测试点另一侧,每个点重复5次,将采集到的数据进行均值处理。实验过程如图2(a)所示。锤击实验的激励装置选用专用于合金材料的力锤,灵敏度为0.21 mv/N,如图2(b)所示。数据采集装置为AC-ADAPTER数据采集器,如图2(c)所示。传感器选择为SERIAL#38306加速度传感器,灵敏度100.6 mv/g,如图2(d)所示。

图2 锤击实验

1.3 实验结果

通过LMS Testlab软件处理锤击实验采集的结果,得到各个工件的模态参数,如表2～4所列。随后通过LMS测试系统进行工件的模态参数处理及分析。前二阶模态参数即可对切削点的动态特性进行较好地评估[11]。

表2 件I锤击实验结果

表3 件Ⅱ锤击实验结果

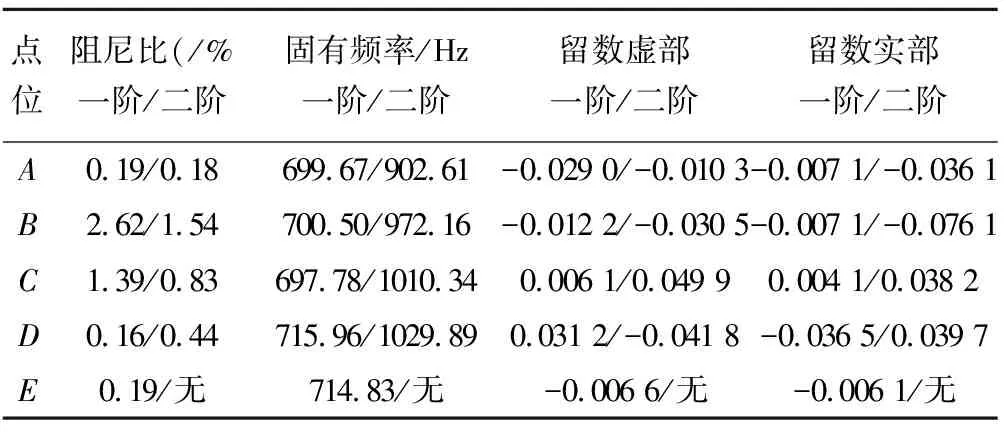
表4 件 Ⅲ 锤击实验结果

2 动态特性影响因素分析

2.1 切削点对动态特性的影响

将表2模态参数进行图像化处理,处理结果如图3所示。

图3 件Ⅰ锤击实验结果

从图3中不难发现,工件的一、二阶固有频率、阻尼比、留数实部和虚部基本以工件的中轴线对称,这验证了1.1节提到的模态参数随工件中轴线的对称性。造成对称点的参数有所差异可能的原因是,在实验过程中,无法完全确保传感器粘贴位置,也无法保证每次锤击位置、力量大小、锤击角度完全一致,故使得结果出现差异。另外,在测试点中,A～D点均在前两阶振型中发生了变形,但是E点,即工件长对称轴上的点,为T型工件二阶振型振动的节点,该点发生的变形为零,在锤击过程中无法得到其二阶振动参数。同时,该点的模态参数为无穷大。故文中在后续叙述中不再考虑薄壁件E点的二阶模态参数。

2.2 材料差异对薄壁件动态特性的影响

获得各个工件的模态参数后,对不同材料的固有频率进行对比分析,如图4所示。图4所示为不同铝合频率的影响趋势图,其中,图4 (a)为不同材料对一阶固有频率的影响,图4(b)为不同材料对二阶固有频率的影响。由图4 (a)可知,除铝合金7 075外,铝合金6 061和铝合金7 050的一阶固有频率均随着实验点向工件中线靠拢而增大,二者涨幅分别为16.23%和19.96%;而铝合金7 075的一阶固有频率随实验点改变产生的变化较小,其变化基本呈现一条直线,整体变化幅度仅为2.54%。由图4 (b)可知,三种典型铝合金的二阶固有频率均随着实验点向工件中线的靠拢而增加,其中,铝合金7 075涨幅为12.36%,铝合金7 050涨幅为13.34%,铝合金6 061涨幅为15.11%。

图4 材料对固有频率的影响趋势图

3 基于实验的动态特性建模

考虑工件切削路径的稳定性预测过程中,工件的模态质量、模态刚度和模态阻尼起到至关重要的作用。为了对工件在整体切削路径上的模态参数进行预测,并进一步对稳定性进行预测,可以根据所得到的模态参数,对其进行拟合以得到工件的动态特性模型。基于1.3节中的锤击实验结果,通过LMS Testlab软件的分析计算,可得到实验薄壁件的模态质量、模态刚度和模态阻尼。

对工件的测试点A～E的模态参数进行拟合。根据文章所进行的实验可知,工件的一阶模态参数拟合点共有五个,二阶模态参数拟合点共有四个,所以分别对一阶和二阶模态参数采用四次多项式和三次多项式进行拟合,拟合结果如图5～7所示,每个实验点的纵轴坐标表示该点的对应模态参数。

图5 件Ⅰ 模态参数拟合

件Ⅰ的拟合结果如图5所示,件Ⅰ一阶模态质量、刚度、阻尼结果如式(1)～(3)所列,二阶模态质量、刚度、阻尼结果如式(4)～(6)所列,从图中不难发现,同阶模态质量和模态刚度的拟合结果曲线走势基本一致,而模态阻尼则与二者有明显区别,这是因为在模态阻尼的计算过程中,加入了阻尼比,阻尼比对计算结果起到了影响作用。

M1(s)=0.001 808s4-0.023 32s3+0.101 9s2-0.169 3s+0.093 3

(1)

D1(s)=28 080s4-3.724e5s3+1.672e6s2-2.822e6s+1.565e6

(2)

C1(s)=0.176 4s4-2.146s3+8.894s2-14.37s+7.763

(3)

M2(s)=-0.002 417s3+0.018 85s2-0.044 63s+0.035 5

(4)

D2(s)=-79 890s3+6.214e5s2-1.448e6s+1.121e6

(5)

C2(s)=-0.042 27s3+0.391 7s2-1.088s+1.028

(6)

件Ⅱ的拟合结果如图6所示,件Ⅱ一阶模态质量、刚度、阻尼结果如式(7)～(9)所列,二阶模态质量、刚度、阻尼结果如式(10)～(12)所列。

图6 件Ⅱ模态参数拟合

M1(s)=-0.000 866 7s4+0.010 3s3-0.037 33s2+0.036 8s+0.020 3

(7)

D1(s)=-18 120s4+2.143e5s3-7.864e5s2+
8.61e5s+2.278e5

(8)

C1(s)=-0.006 871s4+0.101 2s3-0.472 6s2+0.787 6s-0.186 9

(9)

M2(s)=-0.003 467s3+0.036 15s2-0.113 9s+0.117 3

(10)

D2(s)=-81 240s3+9.349e5s2-3.084e6s+3.29e6

(11)

C2(s)=0.712 1s3+5.227s2+11.35s-6.043

(12)

件Ⅲ的拟合结果如图7所示,件Ⅲ一阶模态质量、刚度、阻尼结果如式(13)～(15)所列,二阶模态质量、刚度、阻尼结果如式(16)～(18)所列。

图7 件 Ⅲ 模态参数拟合

M1(s)=0.003 437s4-0.039 19s3+0.151 2s2-0.225 4s+0.113 8

(13)

D1(s)=65 590s4-7.468e3s3+2.878e2s2-4.284e6s+2.163e6

(14)

C1(s)=0.218 2s4-2.247s3+7.037s2-6.551s+1.608

(15)

M2(s)=-0.000 516 7s3+0.005 35s2-0.018 13s+0.021 8

(16)

D2(s)=-12 870s3+1.424e2s2-5.074e5s+6.523e5

(17)

C2(s)=0.166 9s3-1.356s2+3.253s-1.894

(18)

4 结 论

文章对三种不同的典型铝合金材料的薄壁件进行了锤击实验,并提取了动态特性参数。通过分析三种不同材料的动态特性参数随着实验点变化的差异与规律,得到了不同材料对动态特性的影响趋势。最后对模态参数进行前两阶计算结果的多项式拟合。为实际生产中薄壁件切削动态评估及稳定性分析奠定重要基础。研究结论如下。

(1) 铝合金薄壁件的一阶、二阶的固有频率、阻尼比、留数的实部和虚部基本以工件的中轴线对称。

(2) 铝合金7 050和铝合金6 061的一阶固有频率均随着实验点向工件中线靠拢而增大,铝合金7 075的一阶固有频率随实验点改变产生的变化较小;三种典型铝合金的二阶固有频率均随着实验点向工件中线的靠拢而增加。

(3) 三种铝合金材料的模态质量和模态刚度的拟合结果曲线走势基本一致,而模态阻尼则与模态质量和刚度有明显区别。

文中通过对三种不同牌号的铝合金进行锤击实验、动态特性影响因素分析和动态特性建模,得到了考虑切削振动变形的不同铝合金材料平面薄壁件动态特性变化规律,为铝合金薄壁件的切削稳定性预测研究打下重要基础。