多链接复杂网络指数同步的间歇事件触发控制
张宏礼,齐文博,郭 英
(1.岭南师范学院数学与统计学院,广东 湛江 524048;2.青岛理工大学理学院,山东 青岛 266520)
1 引言
复杂网络是由大量互相连接的节点组成的,由于其在生物学、物理学、化学和互联网等各个领域的潜在应用而受到广泛研究[1–4].随着科学的发展,人们的日常生活与许多复杂网络息息相关,例如交通网络、互联网、神经网络、社会网络和电网系统.值得注意的是,许多复杂网络的广泛应用主要取决于耦合系统的动力学行为,包括稳定性、同步性、平稳分布等.尤其是同步性,作为复杂网络的一种重要的动态行为,其在过去几十年中备受关注,并且得到了一些有趣且重要的结果[5–8].文献[7]研究了具有不同节点的复杂网络的同步问题,并提出了两种有效的控制方案,使复杂网络同步到任何平滑的目标动态上.为了实现复杂网络的同步,文献[8]设计了一种新的自适应非线性控制策略.并且,作为复杂网络中的一种常见现象,时滞的存在通常会影响系统的动态特性,这也许会降低系统的性能.事实上,在实际控制问题中,事件触发控制相比于传统的时间触发控制更有效[9].
事件触发控制作为一种重要的采样数据控制得到了广泛关注[10–17].文献[11]提出了一类非线性随机系统的动态事件触发和自触发控制方法.文献[12]研究了一类随机非线性系统的事件触发镇定问题.文献[13]研究了时变时滞记忆神经网络的全局同步控制问题.
上述事件触发控制是对所有的事件进行控制,这可能会导致传输信息过程中一些不必要的浪费.因此,由于间歇控制可以减少传输和控制成本,其可能是一个更好的选择.许多学者已经对间歇控制进行了研究,并且取得了一定的研究结果[18–22].文献[19]基于复杂时滞动态网络的一般模型,利用李雅普诺夫稳定性理论和周期性间歇控制方法,得到了一类复杂时滞动态网络同步的有效判据.文献[20]通过周期间歇控制,得到了基于忆阻器的混沌神经网络指数同步的一些新的充分条件.然而,间歇控制策略的控制时间内是基于时间触发的,这也许会浪费资源.因此,有必要改进间歇控制策略.事实上,文献[21]提出了一种新的周期间歇离散观测控制,虽然这是一种改进,但该策略的控制部分基于周期采样,具有一定的局限性.
鉴于间歇控制和事件触发控制的优点,将事件触发控制引入到间歇控制中具有更广泛的应用价值.文中,文献[23]提出了间歇事件触发控制来研究多智能体网络的一致性问题.而文献[23]提出的间歇事件触发控制策略是静态的.事实上,静态事件触发控制已经引起广泛的研究[23–26],然而静态事件触发控制的事件触发次数高于动态情况,因此具有冗余性.基于上述讨论,为了进一步改进控制策略,本文提出了一种新的间歇动态事件触发策略,该策略的控制部分是基于动态事件触发的,相比于间歇静态事件触发控制策略,极大地减少了事件触发次数.与以往文献相比,本文的主要贡献如下: 1)本文提出了一种新的间歇事件触发策略,即,触发时刻只发生在间歇控制的控制区间,极大地减少了事件触发次数;2)本文考虑的间歇控制的控制增益是自适应的,这具有动态调整的作用.另外通过使用李雅普诺夫方法,本文给出通过间歇事件触发控制实现延迟多链接复杂网络同步的充分条件.
本文的其余部分组织如下: 第2节描述了一些基本符号和数学模型;第3节给出了主要结果;在第4节中,给出了耦合振子系统的应用;第5节给出了一个数值算例和一些仿真结果,以验证文章理论的有效性;最后,第6节给出了一些结论.
2 符号说明
本节给出一些图论的相关介绍.一个有向图G=(M,E)包含节点集M={1,2,···,M}和由弧(h,k)组成的弧集E,这些弧从初始节点k通向终止节点h,对于所有的k ∈M满足(k,k)/∈E.如果每个弧(h,k)被赋予一个正值的权重akh,则有向图G是加权有向图.A=(akh)M×M表示有向图G的权矩阵,其中,akh >0,当且仅当G中存在弧(h,k).一个带权矩阵A的有向图G记为(G,A).如果对于任何一对不同的节点,存在一条从一个节点到另一个节点的有向边,则一个有向图(G,A)是强连通的.
3 模型描述和预备知识
本部分考虑以下具有时变延迟的多链接复杂网络:
注1多链接复杂网络意味着复杂网络的两个节点之间存在不止一条链接,每个节点都有不同的性质.以通信网络为例,人们可以通过电话、电子邮件、MSN、普通信件等方式相互联系,每种通信方式对应一类链接.并且,在时延的影响下,人们接收信息的响应时间也会有所不同.因此,本文设计的具有s个子网络和M个节点的延迟多链接复杂网络更符合实际意义.
考虑如下的一个孤立节点系统:
其中x(t)∈Rm表示孤立节点的状态向量.
令zi(t)=yi(t)-x(t)为同步误差向量.基于系统(1)和(2),得到如下误差系统:
其中,间歇事件触发控制策略ui(t)设计如下:
其中: [tk,sk)代表第k个控制区间,[sk,tk+1)代表第k个休息区间,在间歇事件触发控制策略(4)中di(t)满足
其中:ηi,βi,是正常数,触发时刻由以下触发机制确定:
其中:εi >0,αi >1,pi >0,δi(t)满足
其中:ξi >0,δi(0)>0.
基于系统(3)和间歇事件触发控制策略(4),得到如下的误差系统:
现在,给出一些必要的引理、假设及相关的定义.
定义1延迟多链接复杂网络(1)和孤立节点系统(2)是指数同步的,如果存在常数η >0及M0>0,有
引理1[27]假设函数y(t)是连续非负的,且满足以下的微分不等式:
其中: 0 ≤τ(t)≤,k=0,1,2,···,a1,a2和a3是正常数.如果以下不等式成立:
那么
假设1存在正常数α1和,使得以下不等式成立:
4 主要结果
在本章中,给出确保系统(1)和(2)实现指数同步的一些充分条件.现给出本文的一个主要结果.
定理1如果假设1成立,有向图(G,A)是强连通的且满足以下条件:
其中:ψ ∈(0,1),λ是如下方程的唯一正解:
则系统(1)与系统(2)达到指数同步.
证 考虑如下的李雅普诺夫函数:
其中ci表示有向图(G,A)的拉普拉斯矩阵的第i个余子式.基于文献[28],得到ci >0.同时,可得
结合式(7)和式(14),得到
结合式(15)–(16),可推得
基于式(7),能够得出
将式(18)代入式(17),推得
因此,可得
当di(t)≥,基于式(5),可得出
结合式(20)–(21),得到
将式(22)代入式(19),可得
因此,结合式(13)和式(23),可得
基于文献[28],可得
将式(25)代入式(24)得到
类似地,当t ∈[sk,tk+1),可得
基于式(25),可得
因此,得到
注2在定理1中,本文要求有向图(G,A)是强连通的.事实上,对于非强连通有向图,可以根据文献[29]中的Tarjan算法和文献[30]中的分层算法找到有向图的强连通分支,进而分析它在各个强连通分支中的动力学性质.也就是说,对具有非强连通性的延迟多链接复杂网络的动力学性质的研究可以转化成具有强连通性的延迟多链接复杂网络的研究.因此,基于分层算法,可以用本文的方法类似地得到具有非强连通性的延迟多链接复杂网络的动力学性质.
为了更好地说明参数设定的依据,本文对于定理1给出如下的间歇事件触发控制策略设计流程算法(如表1).

表1 间歇动态事件触发控制策略设计流程算法Table 1 Design process of intermittent dynamic eventtriggered control strategy

表2 参数值Table 2 Parameter values
现在,本文给出如下的一个关于不存在Zeno行为的定理.
定理2如果定理1的所有条件满足,则不存在Zeno行为.
基于事件触发条件
因此,不存在Zeno行为.证毕.
5 振子系统的应用
耦合振子在许多工程和科学领域受到了广泛关注[31–33].本章考虑如下的振子系统:
其中:ξ >0,f是非线性函数.
考虑耦合因素和时变延迟,得到如下的耦合振子系统:
现在,将系统(34)写成如下的紧凑形式:
考虑如下的一个孤立节点系统:
现在,将系统(36)写成如下的紧凑形式:
令Ei(t)=Yi(t)-Y(t).基于系统(34)(36),得到误差系统
定理3如果假设1成立,有向图(G,A)是强连通的且满足以下条件:
其中:ψ ∈(0,1),λ是如下方程的唯一正解:
则系统(34)与系统(35)达到指数同步.
注3在过去几十年中,振子系统受到了学者们的广泛关注,文献[34]研究了具有时变延迟的耦合振子系统中的同步现象.文献[35]考虑了混合多随机权值耦合振子系统的平稳分布和指数稳定性.然而,研究多链接耦合振子系统会更具有实际意义.因此,本文将主要结果应用于具有时变延迟的多链接耦合振子系统中,并设计了一种间歇动态事件触发控制,进而使系统(35)和系统(36)达到指数同步.
注4间歇事件触发控制策略在许多领域具有广泛的实际应用,例如智能交通系统,机械臂系统,互联网系统等[36–39].文献[36]将间歇动态事件触发控制策略应用在双连杆机械臂模型上.文献[37]研究了无人驾驶飞行器的定位问题.本文设计的的间歇动态事件触发控制策略也可以应用于上述两个问题.
6 数值算例
本章给出一些仿真结果来说明理论结果的有效性.令M=6,M={1,2,3,4,5,6}.具有6个节点的耦合振子系统的拓扑结构如图1所示.由图示可知,有向图是强连通的.给出如下的参数:
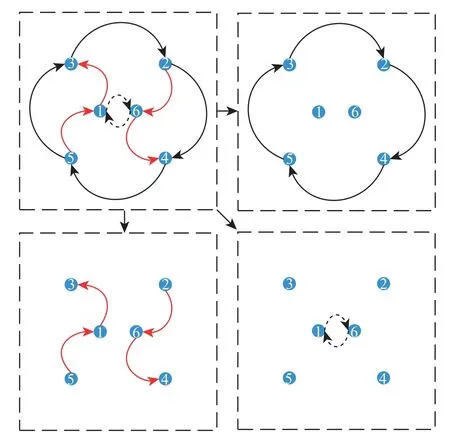
图1 带有6个节点的有向图(G,A1,A2,A3)及其被分成的3个子图(G,A1),(G,A2),(G,A3)Fig.1 A digraph (G,A1,A2,A3) with 6 nodes,which is split into three spanning subgraphs(G,A1),(G,A2),(G,A3)
图2展示了系统(34)的轨迹图.图3代表了误差系统的均方轨迹图.图4展示了6个节点的间歇动态事件触发图.图5展示了6个节点的间歇静态事件触发图.通过图4与图5对比,可以看出间歇动态事件触发控制下的事件触发次数明显小于间歇静态事件触发控制下的情况.因此,间歇动态事件触发控制可以显著减少事件触发次数.综上所述,数值仿真结果表明了本文设计的间歇事件触发控制策略的有效性.

图2 系统(34)的样本轨迹图Fig.2 The sample trajectories figure of system(34)
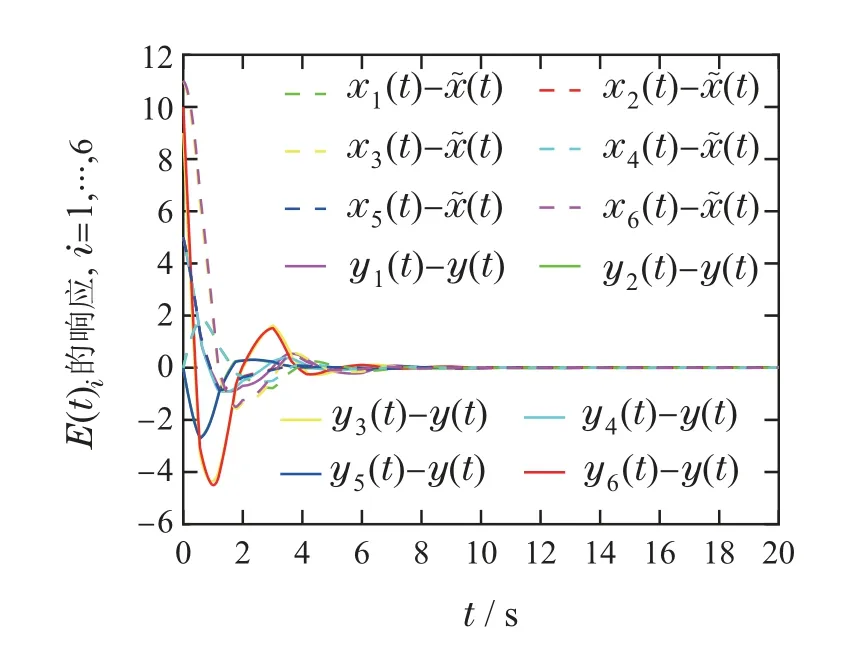
图3 误差系统(37)的均方轨迹图Fig.3 The mean square trajectories figure of error system(37)

图4 6个节点的间歇动态事件触发图Fig.4 Intermittent dynamic event-triggering figure with 6 nodes

图5 6个节点的间歇静态事件触发图Fig.5 Intermittent static event-triggering figure with 6 nodes
7 结论
本文提出一类间歇事件触发控制策略,并使用其研究了延迟多链接复杂网络的指数同步问题.基于图论和李雅普诺夫方法,给出实现延迟多链接复杂网络指数同步的充分条件.最后,本文给出数值仿真验证理论结果的有效性.在未来的工作中,笔者将考虑延迟多链接复杂网络的固定时间同步性问题,并将设计的间歇动态事件触发控制策略应用到电力系统等具有实际意义的问题中.

