新型电力系统惯量特性及其实时感知技术

马骏超，陆承宇，王晨旭，冯启帆，夏杨红，彭 琰

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.浙江大学 电气工程学院，杭州 310027）

0 引言

在实现2030年前碳达峰、2060年前碳中和的“双碳”目标的背景下，电网接入新能源电源的比例迅速上升［1-2］，导致电力系统转动惯量迅速下降，如果不采取有效的频率控制策略，将对系统频率稳定性造成巨大影响［3-7］。频率问题在受端电网中表现尤为突出，2015年某馈入华东电网的特高压直流系统曾发生双极闭锁，瞬时损失功率5 400 MW，导致系统频率最低跌至49.56 Hz，是近10年来首次跌破49.8 Hz，频率越限时间长达数百秒，给新形势下的大电网频率安全问题敲响了警钟。同时相较于常规电源，新能源电源接入点与自然资源密切相关，存在电源接入点分散、单接入点容量较低的特点，对新型电力系统中各电源的控制策略提出了新的要求［8-9］。随着电网“双高”特性的进一步凸显，新型电力系统低转动惯量稳定特性和分布式电源集群主动惯性支撑技术是一个需要深入研究的课题。

电网惯量作为决定电网频率动态行为的关键因素，对研究电网的稳定性问题至关重要。在估计系统惯量方面，传统的惯量估计方法大多是基于测量扰动后的频率和功率变化，通过摇摆方程计算转动惯量。文献［10］采用滑动数据窗口来实现连续计算惯量估计值。文献［11］采用扩展卡尔曼滤波技术和轨迹灵敏度分析，对向量单元记录的扰动数据进行模型参数识别。文献［12］则通过环境测量，采用数据驱动的方法计算系统中转动惯量的数值，避免了对系统进行大扰动，但是该方法需要正确地建立系统的状态空间方程。

随着大量新能源发电单元通过电力电子设备渗入电网，替代传统同步发电机向电网输出功率，导致电网的元件组成复杂多变，虚拟惯量控制、下垂控制、虚拟同步发电机的引入等使得惯量不确定因素不断增加［13-14］。惯量作为决定电网受扰后频率动态行为的重要特征参数，在新能源电力系统中的表现形式复杂多样，其中跟网型逆变器的惯量与发电机转子提供的惯量具有显著的物理差异，其本质仍是功率源［15］。由于稳定性的限制，构网型逆变器提供的转动惯量H非常有限，更多地提供了阻尼D［16］，因此在新型电力系统中仅采用转动惯量来表示系统中的惯量水平难以准确反映扰动下的频率特性，需要厘清不同惯量的响应过程，研究新型电力系统的惯量特性并提出惯量的实时感知技术。

此外，在含有虚拟惯性控制的新能源占比较高的电网中，由于电力电子调频装置动作速度较快，大规模新能源的消纳使得电网的频率特性更加复杂。仅采用发电机转子的转动惯量和一次调频来表示系统的频率响应模型难以有效拟合实际的频率变化情况［17-18］，需要在明确不同机组的惯量响应过程、实时感知惯量的基础上，建立适合于新型电力系统的等值惯量模型。

本文首先介绍传统同步发电机的惯量特性，在此基础上研究新能源机组的惯量响应过程并建立相应的数学模型，厘清不同惯量的基本概念。然后结合机组在地理空间上的分布特性，合理划分区域，提出采用改进多项式曲线拟合法和系统辨识法测量系统中惯量的具体数值。最后通过IEEE 9 节点系统模型仿真分析新能源机组提供的虚拟惯量对系统频率的影响，并对系统的惯量水平进行定量评估。

1 新型电力系统虚拟惯量及其数学模型

新能源机组包含光伏、风电、储能、制氢等多种异构式分布电源，其动态特性完全不同于同步发电机，传统摇摆方程难以全面刻画新型电力系统频率受扰后的动态过程，因此对含有大量新能源机组的新型电力系统的惯量特性进行研究。为了厘清不同设备在频率扰动下的响应过程，需要对同步发电机和新能源机组、负荷的惯量响应过程建立相应的数学模型。

1.1 同步发电机惯量响应过程及数学模型

首先简要介绍同步发电机的惯量响应过程。在仅有发电机作为电源的传统电力系统中，电力系统的惯性描述了表示系统机电特性的摇摆方程：

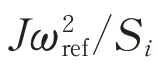
同步发电机及调速器的模型可以用负载功率变化与频率偏差的传递函数表示，如图1所示并表示为式（2）中的传递函数G，其中：s为拉普拉斯算子；TG为调速器系数；FHP为涡轮HP系数；TRH为再热器时间常数；TCH为主入口容积时间常数；ΔPD-pu为阻尼环节吸收的功率；Δfr-pu为系统频率与额定频率之差；1/R发电机调速器的调差系数。

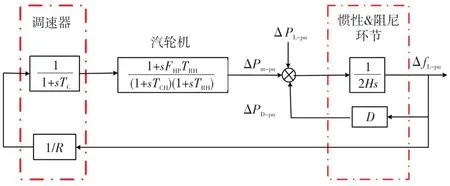
图1 同步发电机及其调速器数学模型Fig.1 Mathematic model of synchronous generator and governor

不同惯量的同步发电机频率响应如图2所示。随着发电机惯性的增加，系统受到扰动后的RoCoF（频率变化率）降低，频率最低点抬升。由于发电机组的调速器及自动调频装置调节汽轮机汽门或水轮机导向叶片开度需要一定的时间，一次调频和二次调频动作较慢，响应初期只有惯性作用，惯性越大则将为一次调频争取越多时间，从而防止低频减载的误动，有利于系统的频率稳定。

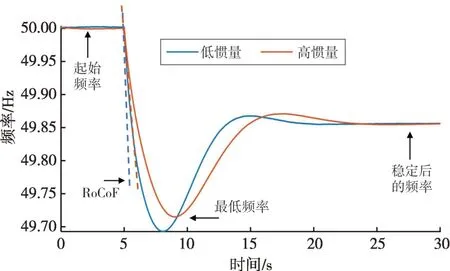
图2 不同惯量的同步发电机频率响应Fig.2 Frequency responses of a synchronous generator at different rotational inertias

1.2 新能源机组惯量响应过程及数学模型

可再生能源发电单元与传统的集中式发电机组有明显差异，主要体现为以下3个方面［13，18］：

1）新能源发电单元通常缺少常规发电单元中可用来抵消频率变化的能量缓冲环节，其中不涉及旋转部件且电容器中存储的能量非常少，可近似认为其惯量为零。

2）可再生能源发电单元通常通过电力电子换流装置连接，该电力电子变换器将发电机与电网完全或部分分离，阻隔了发电机转速与系统频率之间的联系，导致换流器连接的新能源发电单元无法直接对整个系统的惯量做出贡献。

3）新能源发电单元采用的调频装置动作较快，在时间尺度上与发电机转子的惯性响应更为接近，虚拟惯性对电网频率的支撑使得频率变化更为复杂。

因此，亟需研究全方位评估电网惯量特征的方法体系，对新能源电力系统的惯量动态特征进行分析。

1.2.1 同步惯量与非同步惯量

新型电力系统中存在的惯量按照频率与能量的关系可以分为同步惯量和非同步惯量，如图3所示，其中：ωr为同步发电机的角频率；PVIC为与频率调节相关的控制环节产生的功率变化指令；PPRC为系统的基准功率；Pref为系统加入非同步惯量后的功率参考值。

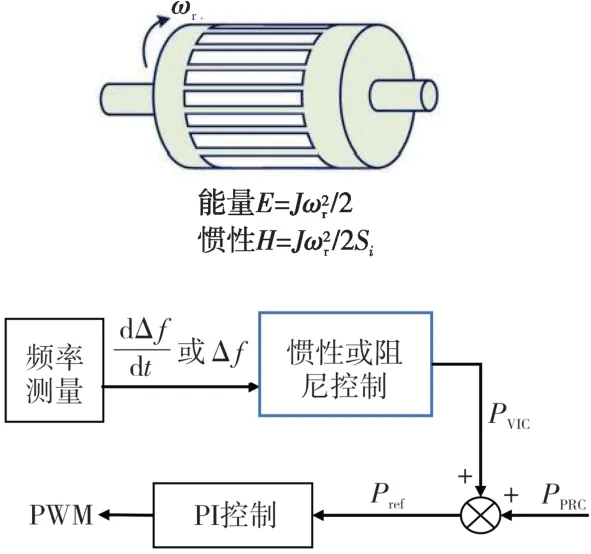
图3 同步惯量和非同步惯量Fig.3 The synchronous inertia and asynchronous inertia

同步发电机转子固有的物理特性就是通过释放转子中储存的能量来响应负载的变化，频率的变化是转子动能释放的结果，因此这种基于摇摆方程的惯量称为同步惯量。非同步惯量的频率调节特点是根据并网点频率的变化来调节发出的有功功率，主要由系统中存在的各种具有频率调节能力的电源提供，如新能源发电、储能系统以及同步发电机的调速器（包括一次调频和二次调频）等。由于测量与控制的延迟，存在一定的滞后，即频率已经下降了，控制策略才开始起作用［13-14］。两种惯量的对比如表1所示。

表1 同步惯量与非同步惯量对比Table 1 Comparison of the synchronous inertia and asynchronous inertia

尽管系统中非同步惯量的控制策略不同，但可以系统地表示和区分发电机调速器以及不同新能源机组具有的等效虚拟惯量的作用。虚拟惯量根据拓扑的不同可分为基于RoCoF 的虚拟惯量（或称作虚拟转动惯量）、基于频率偏差或功率-频率下垂特性的虚拟惯量（或称作虚拟阻尼）、基于频率积分的虚拟惯量。系统的同步惯量与非同步惯量整体模型如图4所示，其中：∆f为系统的频率与额定频率之差；∆P为系统中电源和负荷的功率变化，下标sync 和non-sync 分别代表同步惯量和非同步惯量，下标gov表示发电机调速器，下标VI表示系统中的虚拟惯量；HVI、DVI、KVI为不同虚拟惯量的增益；延时和惯性环节代表控制器的响应滞后于频率变化。

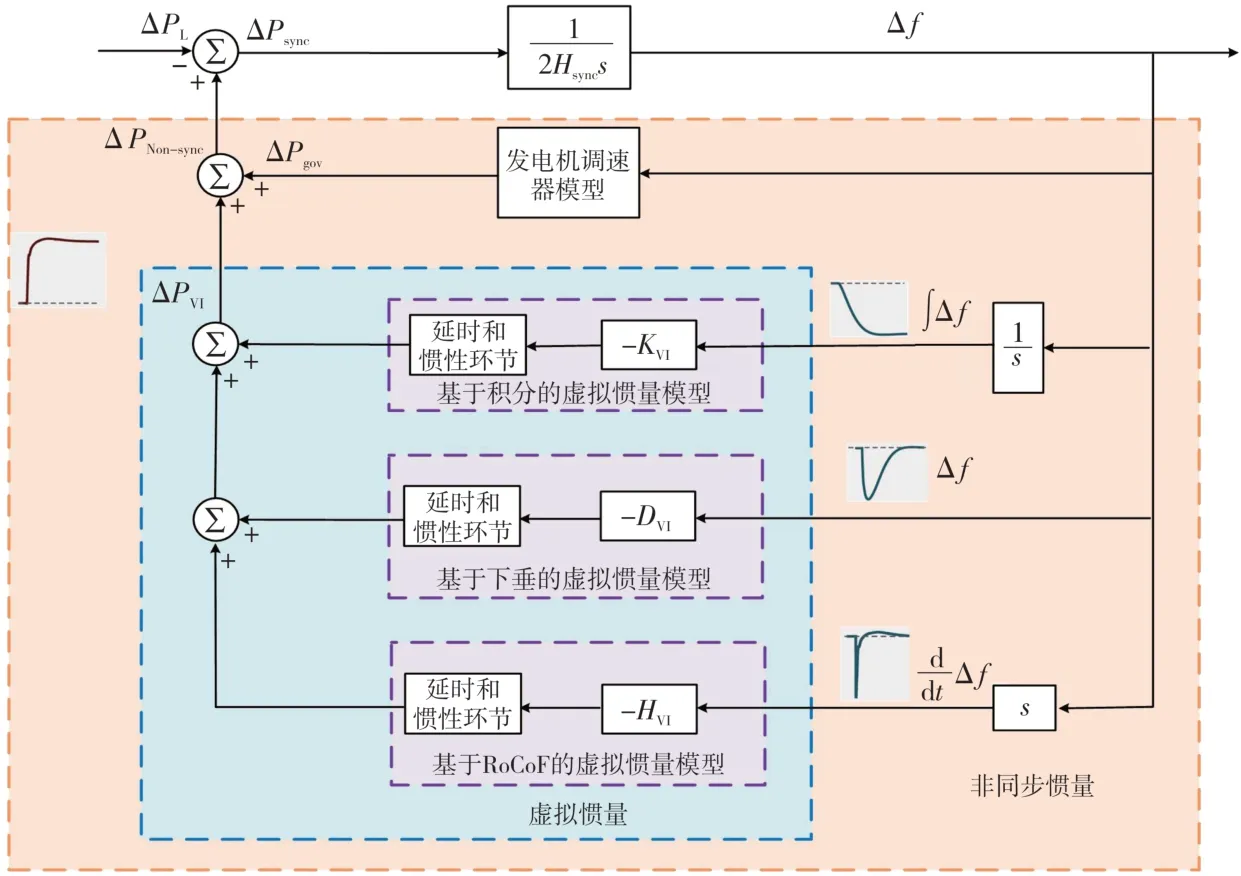
图4 同步惯量和非同步惯量整体模型Fig.4 The aggregated model of synchronous inertia and asynchronous inertia

1.2.2 新能源机组虚拟惯量

目前电网中存在的新能源机组依靠逆变器向电网输送功率，分为跟网型控制（电流源型新能源机组）和构网型控制（电压源型新能源机组）两类，如图5所示，其中：Cpv为新能源出口侧的滤波电容；Cdc为直流链路电容；d1和d2分别为DC/DC变流器和DC/AC逆变器开关管的占空比；θ和f分别为锁相环输出的相位角和频率；θref和Vref分别为构网型控制的电压参考相位角和幅值；Pref和Qref分别为构网型控制输出的有功、无功功率参考值。

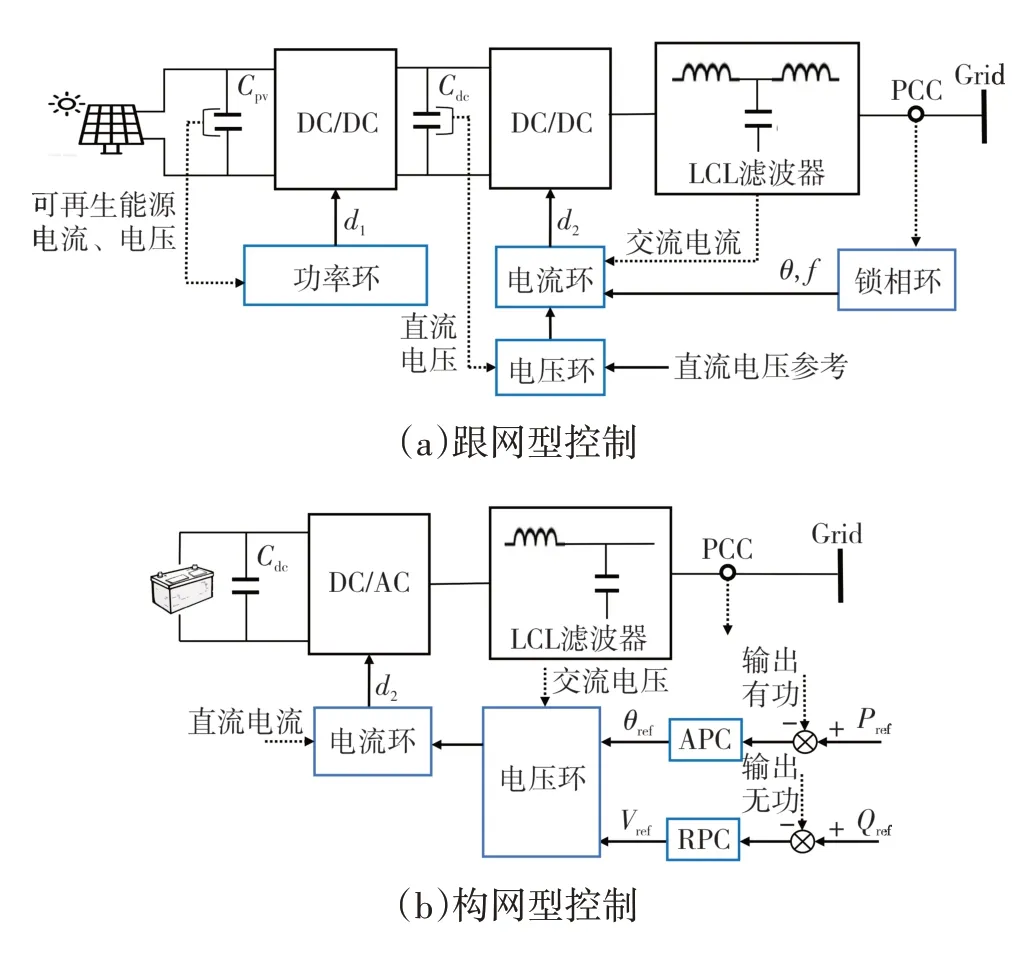
图5 跟网型控制与构网型控制Fig.5 Grid-following control and grid-forming control

跟网型控制策略通过锁相环跟踪并网点的电压相位，矢量电流控制基于并网点电压的dq参考系定向，新能源机组作为功率源运行。构网型控制策略通过APC（有功功率控制）和APC（无功功率控制）调节并网变流器的输出有功和无功功率，产生电压基准的相位角和电压幅值，并通过电压控制回路调节逆变器输出的电压；该控制策略本身可以为系统提供频率和电压支撑，但是需要储能环节提供稳定的直流电压和额外的功率支撑。

通常情况下采用跟网型控制策略的新能源机组工作于最大可用功率点，其出力直接受天气影响，不具备在频率降低时发出额外有功功率的能力［19］。因此，为新能源机组配备储能系统，可提升系统的整体功率可调性，系统可根据频率变化主动调整其输出功率，是实现频率支撑的有效途径［20-21］。文献［22］利用光伏变流器直流侧滤波电容作为储能设备，将电容储存的能量等效为转子惯量，该控制策略需要配置较大的电容。此外，风电、光伏可以通过主动降载运行来预先储备一部分功率，在功率可调裕量内，变流器根据母线频率自适应调整风电、光伏出力，进而主动支撑频率［23-24］。

对于采用跟网型控制策略的新能源机组而言，其输出电流需要跟随电网电压相位的变化，具有功率源的特征，控制器的响应滞后于频率变化。逆变器在检测到电网频率发生变化或接收到释放额外功率的指令后，根据RoCoF或Δf调整输出的有功功率参考值，经由内环的PI 控制完成对参考值的追踪。考虑到通信环节，逆变器和滤波器、隔离变压器等连接组件的延迟性，机组的频率响应速度相对较慢，因此采用包含逆变器时间常数和连接组件时间常数的延迟或惯性环节的简化惯量模型来表示跟网型控制的频率特性：

式中：HVI和DVI分别为虚拟转动惯量、虚拟阻尼的增益；Gdelay为图4 中的延时和惯性环节，可以通过传递函数近似表示。

与同步发电机相比，跟网型逆变器调节有功功率存在一定的滞后，不能在扰动的瞬间响应频率的变化，必须依靠同步惯量和阻尼。但是跟网型逆变器的响应速度比同步发电机的一次调频更快，在时间尺度上与发电机转子的惯性响应更为接近，采用较小的虚拟惯量即可实现与发电机调速器相比更好的调频效果。如图6所示，对不含虚拟惯量和含有光伏机组提供的虚拟惯量的系统进行负荷阶跃扰动，其中发电机调速器的调差系数（1/R）与虚拟阻尼（DVI）之和相等，系统中的其他系数均相等。由图6可知含有虚拟阻尼的系统频率最低点较高，因此对新能源发电采用虚拟惯性控制策略，有利于系统的频率稳定。

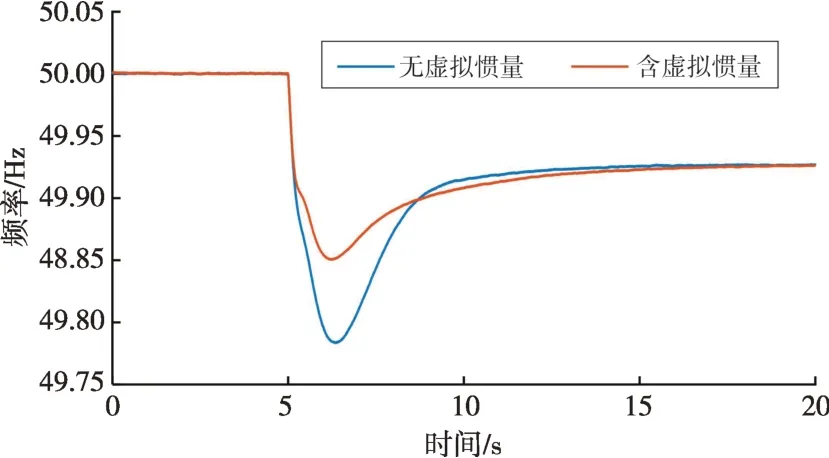
图6 有、无跟网型控制虚拟惯量的频率响应对比Fig.6 Comparison of frequency response with or without grid-following virtual inertia control

采用构网型控制的新能源机组可以根据输出的有功功率来调节并网点电压的相位及频率，具有电压源的特征，并网点电压的相位不会发生突变，能够不依靠电网独立运行，实现组网功能。因此，构网型控制与同步发电机类似，无需添加其他控制策略即可实现对电网频率的主动支撑。由于构网型控制由输出的有功功率决定频率，构网型控制具有的虚拟惯量可以视为同步惯量和阻尼，与同步发电机组的转子和阻尼具有相同的作用。常见的构网型控制包括下垂控制和VSG（虚拟同步发电机）控制，其频率-功率特性为：

构网型逆变器与同步发电机的频率响应对比如图7所示。相较于同步发电机，构网型逆变器具有更快的一次调频速度，与具有相同调差系数和阻尼的发电机相比，受到相同的负荷阶跃变化的扰动后，频率更容易恢复稳定。但是构网型具有较低的转动惯量，系统受到扰动后初始的RoCoF较大。

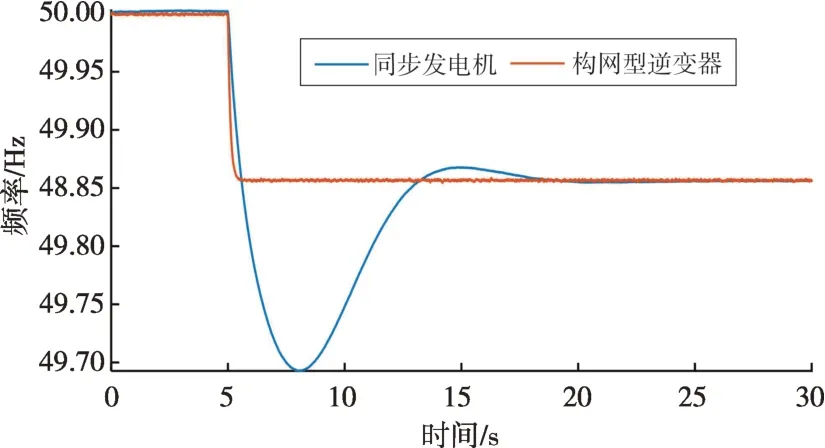
图7 构网型逆变器与同步发电机的频率响应对比Fig.7 Comparison of frequency responses of grid-forming inverter and synchronous generator

采用跟网型控制和构网型控制的新能源机组的虚拟惯量特征总结见表2。

表2 跟网型控制与构网型控制虚拟惯量对比Table 2 Comparison of virtual inertias of grid-following control and grid-forming control

2 电力系统惯量时空分布模型和实时感知方法

2.1 惯量的时空变化与区域划分

复杂、多区域网络结构受到扰动后，电气距离较远的各节点频率量测不一定一致［25］，考虑新能源机组出力随机性与源荷空间分布差异性，需要建立以新能源为主体的新型电力系统惯量时空分布模型。

根据传统同步发电机、新能源机组、负荷等在地理空间上的分布特性，以机组动态特性相似及电气距离最短为指标，合理划分区域。如图8所示，同类型、控制策略相同、电气距离较近的机组被划分为一个区域。综合考虑区域内不同设备的惯量响应过程，计算出整个系统的等效惯量。

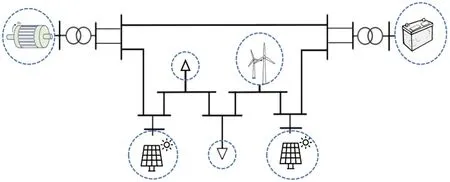
图8 多区域电力系统Fig.8 Multi-regional power system

2.2 同步惯量、非同步惯量实时感知方法

2.2.1 测量同步惯量-改进多项式曲线拟合法

负荷的变化会导致系统RoCoF 和Δf的变化，如图9所示。

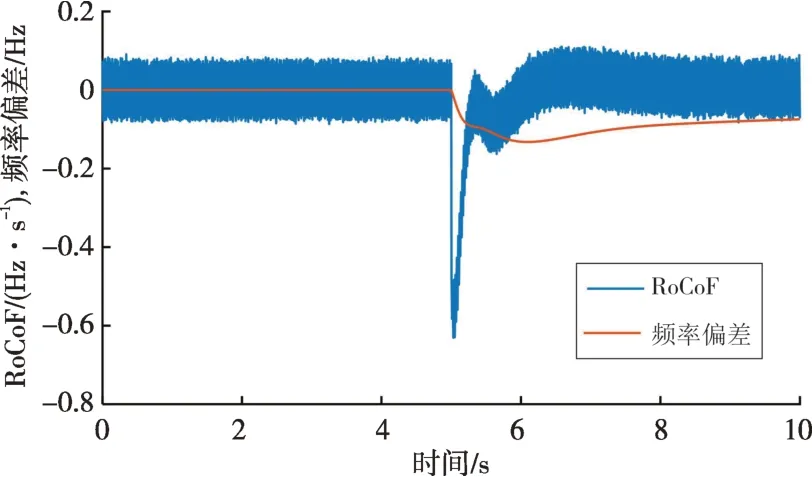
图9 系统受扰动后的RoCoF与频率偏差Fig.9 RoCoF and frequency deviations after system disturbance

由式（1）可知，在扰动发生的瞬间，系统的频率偏差Δf=0，同步发电机的调速器和阻尼的影响只与Δf有关，对频率的变化率没有影响，DΔfpu项和ΔPm-pu项可以忽略。此时采用跟网型控制的机组提供的虚拟惯量还未发生作用，所以只有系统的同步惯量会影响RoCoF 的变化。对于一个已知的扰动，如果可以准确地量测扰动初始时刻（t=t0）的RoCoF，就能计算出系统的同步惯量：

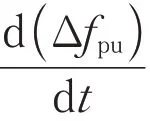
式（6）中多项式每一项的系数A0，A1，…，An由曲线拟合的结果所决定，在t=t0时刻，多项式的主导部分是A1t，由此可以求得：

在传统电网中，由于扰动后的较短时间内频率的变化主要由发电机的转动惯量决定，曲线较为简单，采用较低阶的多项式拟合频率响应即可获得较为准确的结果［26］。在含有虚拟惯性控制的新能源占比较高的电网中，频率响应较为复杂，传统方法测得的RoCoF 与实际情况可能误差较大，因此测得的系统惯性不准确。但是，多项式拟合并非阶数越高越好。本文提出了改进多项式曲线拟合的方法，可以更为准确地测量系统的Δfpu，进一步可以获得同步惯量。

图10展示了进行改进多项式曲线拟合的过程，其中输入为频率偏差Δf和功率变化ΔP，输出为系统的同步惯量H。首先通过式（5），利用量测的RoCoF计算得到同步惯量的粗略估计值HRoCoF。然后初始化曲线拟合阶数n=2，通过式（6）、式（7）进行曲线拟合得到对应的同步惯量Hn，如果Hn与HRoCoF偏差较大则表明拟合结果不够理想，应舍去。当n+1 阶多项式拟合结果和n阶多项式拟合结果之差ΔH在容许的数值（本文为2.5%）之内时，拟合得到的同步惯量较为准确，输出H作为最终的结果。若ΔH不满足上述条件，则令n=n+1，重新进行曲线拟合。

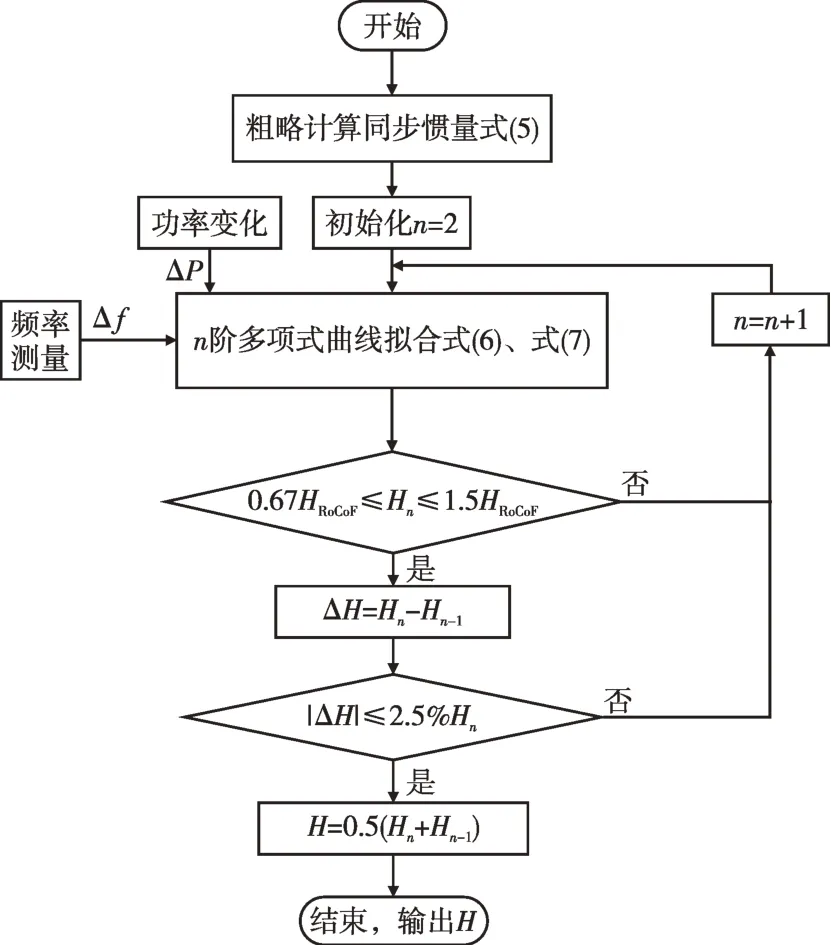
图10 改进多项式曲线拟合法测量同步惯量Fig.10 Synchronous inertia measurement using improved polynomial curve fitting method

2.2.2 测量区域内惯量-系统辨识法

改进多项式曲线拟合法测量同步惯量只适用于规模小且网络结构简单的孤岛运行的系统，系统内各点频率几乎一致，且系统中的同步惯量全部来源于系统内的同步发电机和构网型逆变器。因此，该系统的频率变化只与系统内的惯量有关，将同步惯量的影响分离出去后即可得到非同步惯量的频率-功率响应。但是在系统并入大电网运行时，系统内的频率变化受大电网影响严重，无法确定系统内的同步惯量。此外，若某一区域中只包含跟网型逆变器，由于跟网型逆变器需要其他电源提供电压支撑，不能独立运行，必须排除区域外惯量的影响。

在某一区域进行负荷阶跃扰动，获得区域内的频率变化和区域内跟网型逆变器的功率变化后，在已知系统的基本拓扑和输入、输出的情况下，采用系统辨识的方法可以确定跟网型逆变器提供的非同步惯量，即用传递函数去拟合基于RoCoF、频率偏差、频率积分的虚拟惯量以及测量与控制的延迟。如果跟网型逆变器的功率变化难以直接测量，根据功率平衡原理，可以采用负荷功率减去区域外功率变化的方法间接获取。

与多项式曲线拟合类似，系统辨识的效果与选择的传递函数阶数有关。采用一阶系统拟合计算复杂度低，但是辨识准确度可能受限；采用高阶系统对提高辨识准确度有一定帮助，但是计算复杂度高，多区域聚合后形成的惯量模型表达式将更加复杂。因此，需要选取合适的传递函数阶数。本文提出的系统辨识法测量非同步惯量如图11所示，其中Gdelay为延时和惯性环节。首先用一阶系统拟合输入、输出曲线（频率变化曲线-功率变化曲线），其中传递函数的极点数目p=1，零点数目z=0。如果系统辨识的准确度在90%以上，且进行系统辨识的传递函数的零点数目和极点数目增加1 后，对系统辨识的准确度几乎没有影响，则输出系统辨识的结果，根据系统辨识的结果可以确定虚拟惯量的大小和延时、惯性环节的传递函数表达式；反之若辨识准确度不高，则应当逐渐增加传递函数的零点数目和阶次，直到系统辨识的结果符合要求为止。

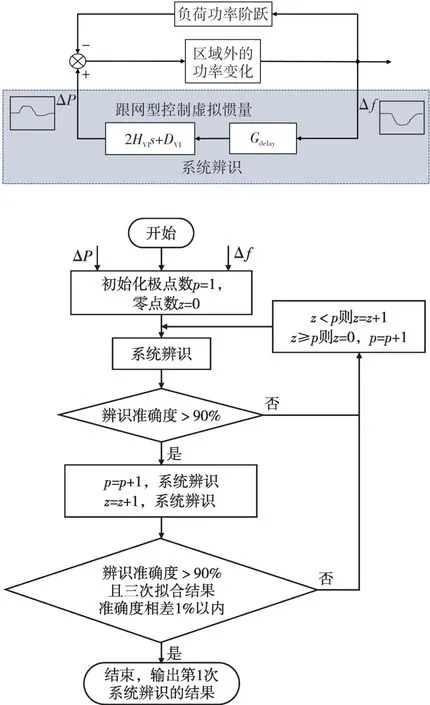
图11 系统辨识法测量非同步惯量Fig.11 Asynchronous inertia measurement using system identification method

2.3 电力系统惯量分布模型和系统等效惯量

对于多机系统，考虑到光伏、风电等新能源机组出力的时变特性，需要研究在同一区域不同时间段的惯量变化；在同一时间尺度上，不同区域的惯量特性也不尽相同。不同时间段测量的不同区域的惯量，如图12所示，该惯量水平可用于表示转动惯量，也可以表示阻尼、虚拟惯量等。在多个惯量不足的相邻区域内，受到扰动后更容易发生频率越限事故。

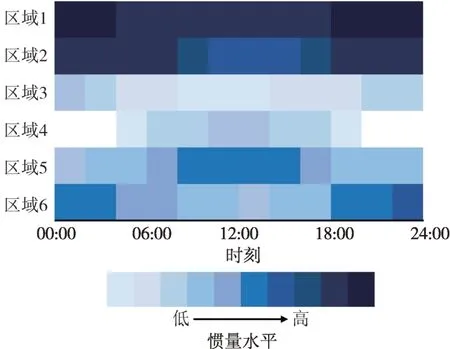
图12 不同时间、不同区域惯量水平对比Fig.12 Comparison of inertia levels in different regions at different times

进一步地，不同区域的惯量可以聚合为系统的惯量模型，其中相同类型的惯量按照不同机组的基准功率进行合并，整个系统的惯量Hsys可以表示为：

式中：Ssys为多个区域形成的系统的功率基准；N为区域总数；Sj和Hj分别为区域j内机组的功率基准、转动惯量（同步惯量和虚拟惯量）。同理阻尼和基于频率积分的惯量也符合式（8）的聚合方式，最终形成整个系统的惯量模型如图4所示。该惯量模型对应的频率变化视为整个系统惯量中心的频率变化，由于机电扰动可在电网中长时间传播，且机电波的传播速度远小于光速，系统中各节点的频率变化不完全一致，但是均呈现出与惯量中心的频率变化类似的趋势［27］。

3 案例分析与频率响应性能评估

3.1 惯量感知性能分析

采用IEEE 9节点系统进行案例分析，如图13所示，其中新能源渗透率为50%，同步发电机转子提供的同步惯量H=1.5 s（基准功率10 MVA），同步发电机的调差系数1/R=20，跟网型逆变器含有DVI=5的虚拟阻尼，在第1 s时加入3%（0.3 MW）的负荷阶跃变化。

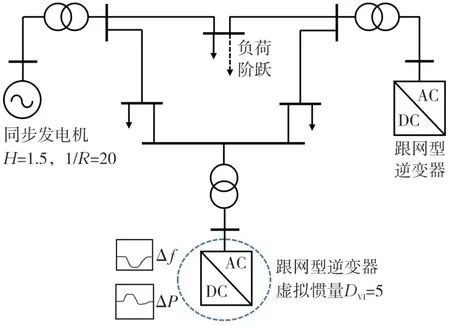
图13 案例分析-IEEE 9节点系统Fig.13 Case analysis of IEEE 9-node system

首先进行同步惯量的估计，直接选取量测的最大RoCoF 进行计算，代入式（5）得到的HRoCoF=1.21，与实际值偏差较大。在采用曲线拟合之前需要首先确定曲线拟合的时间，其中较长时间的频率偏差曲线需要更高阶的多项式来拟合，较短时间的频率偏差曲线需要更精准的频率量测和更精确的拟合精度，本文采用第1 s至第1.5 s的频率偏差曲线进行拟合。采用传统的曲线拟合方法，选取4阶多项式进行拟合，得到：

经曲线拟合得到的频率偏差曲线和实际的频率偏差曲线对比如图14所示，两者吻合程度较高。其中A1=-0.706 5，ΔP=-0.029 8，代入式（7）可以求得H=2.13，与实际值偏差较大。采用本文提出的改进多项式拟合法后，拟合结果如表3所示，求得H=1.47，更符合实际值。

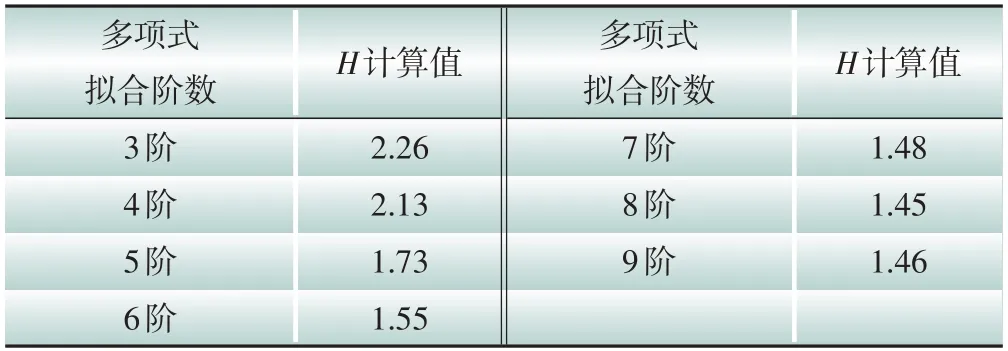
表3 同步惯量计算值Table 3 Calculations of synchronous inertia

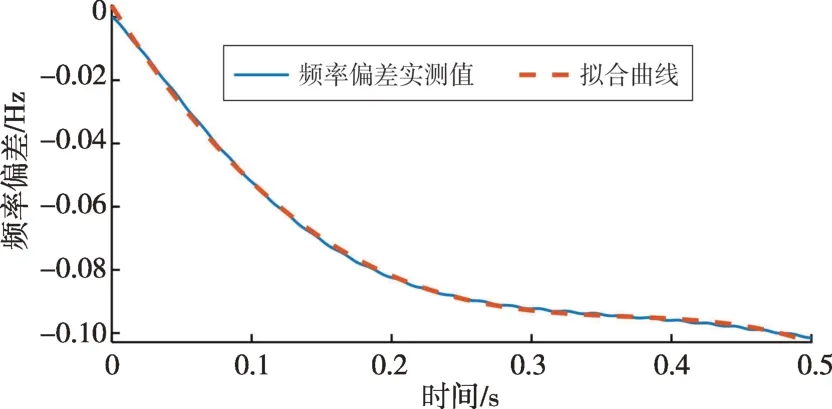
图14 频率偏差实测值与4阶多项式拟合曲线对比Fig.14 Comparison of measured frequency deviations and fourth-order polynomial fitting curve

然后采用系统辨识法进行非同步惯量的估计。将提供虚拟惯量的跟网型逆变器划分为一个区域，单独测量区域内的频率变化和跟网型逆变器发出功率的变化，采用图11 中的方法，得到跟网型控制提供的虚拟惯量的表达式为：

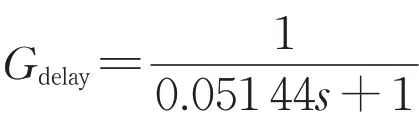
表4 系统辨识结果Table 4 System identification results

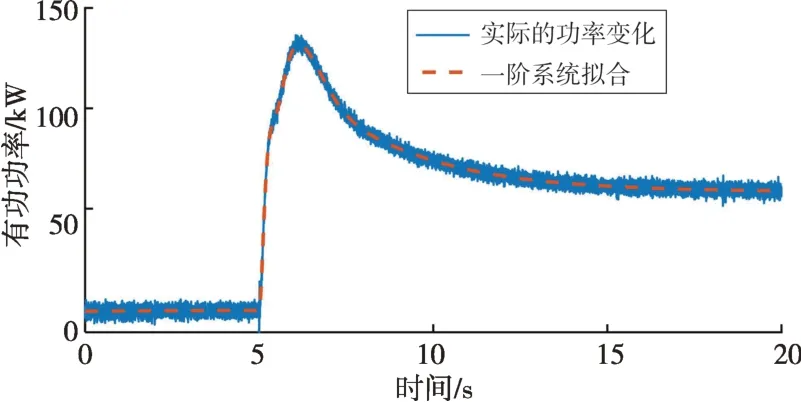
图15 功率实测值与一阶系统拟合曲线对比Fig.15 Comparation of measured power and the first-order system curve fitting

3.2 应对电网阶跃扰动性能评估

以该IEEE 9 节点测试系统为例，进行系统等效惯量评估，根据测量的转动惯量、新能源发电含有的虚拟惯量和发电机调速器模型，结合各机组的额定功率和容量，形成功率基准为10 MW的等值惯量数学模型。用该等值惯量模型模拟系统受到3%负荷扰动后的频率变化，并与测试系统的仿真结果进行对比，如图16所示。实际测量的频率变化与采用等值惯量模型得到的频率变化相似，这是由于实际系统的线路中含有电感、电容，拟合得到的惯量偏小，如果等值惯量模型受到扰动后未发生频率越限，那么实际系统也不会发生频率越限。

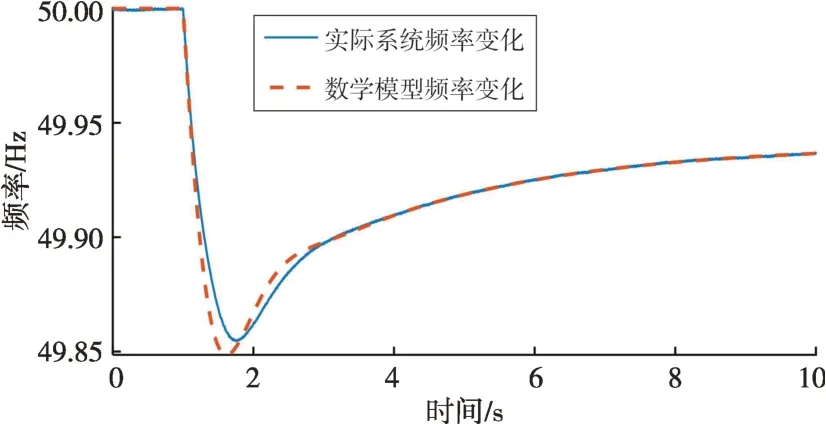
图16 时域仿真与等值惯量模型频率响应曲线对比Fig.16 Comparison of time domain simulation and frequency response curve of equivalent inertia model

对比不同类型的虚拟惯量的作用，其中跟网型逆变器分别采用了基于频率偏差的虚拟惯性（DVI=5）和基于RoCoF的虚拟惯性（2HVI=5）。系统的频率响应如图17所示，对应的跟网型逆变器的功率变化如图18所示。与无任何虚拟惯量的系统相比，加入基于RoCoF 的虚拟惯量（虚拟转动惯量）在扰动发生后的短时间内即可降低系统的频率变化率。转动惯量高的系统频率变化更慢，需要较长时间恢复稳定，对提升最低频率的贡献不大，对稳定后的系统频率没有影响。此外，跟网型逆变器在动态过程中需要快速跟踪功率指令的变化，对频率的准确测量也是影响控制效果的关键因素。加入基于频率偏差的虚拟惯性（虚拟阻尼）在扰动初期并不能降低RoCoF，但更为有效地抬升了系统的频率最低点，并且在频率稳定之后逆变器释放额外的功率以提升系统频率。因此，系统在扰动后发生低频减载的主要原因是缺少阻尼。

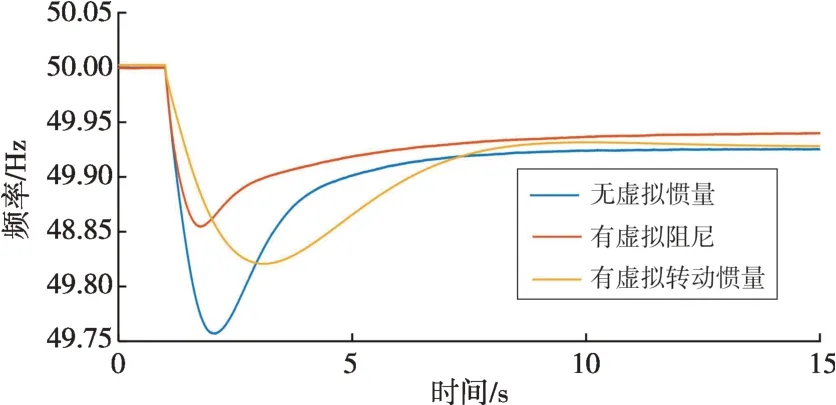
图17 不同类型虚拟惯量频率响应对比Fig.17 Comparison of frequency responses of different types of virtual inertias

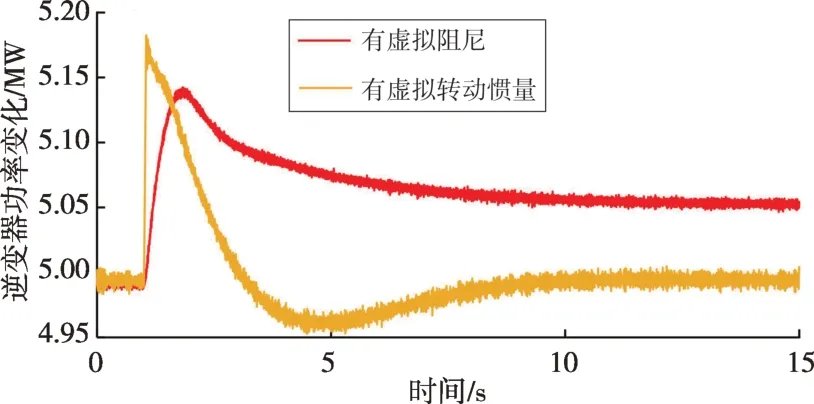
图18 跟网型逆变器功率变化Fig.18 Power change of grid-following inverter

在3%负荷阶跃作用下，评价惯量是否充足的指标包括最低频率、稳定后频率、最大RoCoF、稳定所需时间、不触发低频减载（低于49.7 Hz）系统可承受的最大负荷阶跃，具体见表5。可以看出，含新能源提供的虚拟惯量的系统频率稳定性显著地高于不含虚拟惯量的系统。

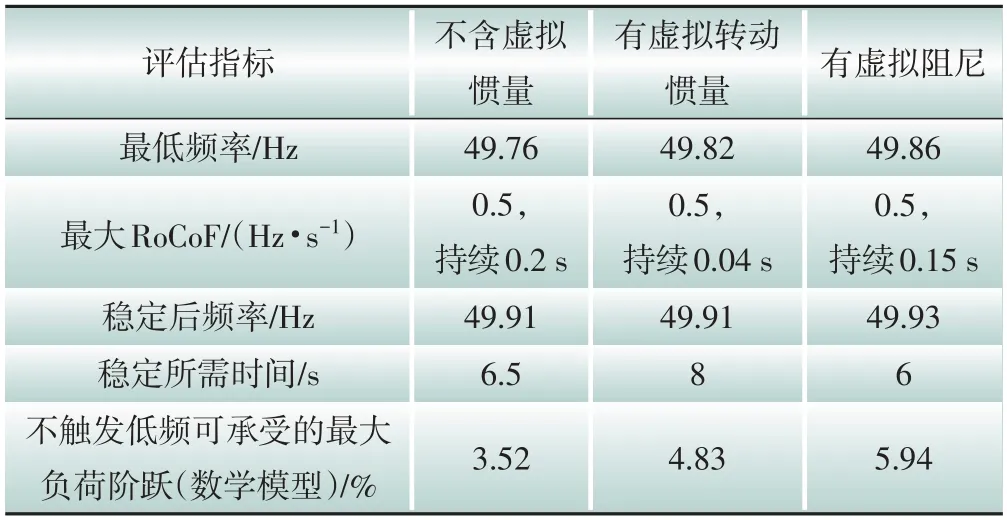
表5 惯量是否充足的评估指标Table 5 Indicators of the adequacy of inertia

由表5 与图17 可知，无论采用跟网型控制还是构网型控制，新能源机组提供的惯量并不能有效降低扰动瞬间的RoCoF，因此在含有高比例新能源的系统中，RoCoF 的瞬时值不宜作为评价惯量是否充足或进行低频减载的标准。由于电力电子调频装置的动作速度快于发电机调速器的一次调频，虚拟惯量对提升系统最低频率的作用更加明显。在新能源比例渗透率较高的情况下，应首先考虑受到扰动后的最低频率和不触发低频减载时系统可承受的最大负荷阶跃作为惯量是否充足的指标。此外，新能源出力的随机性或间歇性可能导致提供虚拟惯量的机组出现惯量水平不足，因此需要合理安排机组出力和提高惯量管理能力。

4 结语

本文揭示了电力系统中惯量的特征，明确了新能源机组的频率响应特性并建立了对应的数学模型，提出了对新型电力系统的同步惯量和非同步惯量的实时感知方法，最后在IEEE 9节点系统中对低转动惯量场景下的频率稳定特性进行评估。

本文提出的虚拟惯量数学模型准确地刻画了同步发电机、跟网型和构网型逆变器的惯量响应过程。提出的改进多项式曲线拟合法可以准确测量系统中的转动惯量，相较于传统的直接测量法和曲线拟合法更适用于新能源渗透率较高的新型电力系统。提出的系统辨识法可以准确测量某一区域内的惯量，具有足够的准确度和较低的计算复杂度，在此基础上形成了电力系统惯量时空分布模型和惯量的等值数学模型。通过案例分析虚拟惯量对低转动惯量电力系统频率的影响，为系统频率稳定提供决策分析支持。