自由面碎冰浮冰环境高速入水动力学特性

张润东，段金雄，孙铁志，2，*，张桂勇，2

(1.大连理工大学 船舶工程学院，大连 116024；2.工业装备结构分析优化与CAE 软件全国重点实验室，大连 116024)

0 引 言

航行体高速入水问题普遍存在于鱼雷空投、跨介质航行器入水以及空天飞行器回收等方面[1-2]，其入水冲击、入水空泡以及入水弹道等问题受到广泛关注[3]。航行体高速入水过程涉及气、液、固强耦合作用，过程中往往伴随着复杂的多相流动、剧烈的入水砰击以及入水空泡的非线性发展等现象[4-5]，严重威胁入水航行体的安全性和可靠性。受到全球温室效应的影响，极地区域冰层加速融化形成了部分散碎浮冰与小厚度层冰覆盖区域，这为极地高速航行器的投放入水创造了适宜的操作环境，但是相较于传统的无冰环境入水问题，漂浮碎冰环境下的航行体入水过程中冰结构与航行体之间的碰撞破坏将进一步增加碎冰环境下航行体高速入水过程的复杂性[6]。因此针对碎冰环境下航行体高速入水过程开展相关数值仿真研究对认识与把握碎冰复杂界面下的高速入水问题具有极大的学术与工程研究价值。

目前国内外学者针对不同环境下的高速入水空泡发展过程已经开展了广泛研究，形成了一定的成果积累。在实验方面，Schaffar等[7]进行了超空泡航行体高速入水实验，并将试验结果与仿真结果进行了分析比对。Shi等[8]研究了入水航行体弹头形状、撞击速度和撞击角度对入水空泡动力学特性的影响。张东晓等[9]基于高速摄影技术，利用实验的方法研究得到了冰孔约束条件下的弹丸入水空泡演化特性，并进一步总结了入水初速度对冰孔约束下弹丸入水运动特性的影响。目前大多数实验主要是研究低速航行体的入水空泡发展过程，高速入水试验流场演化剧烈，实验精确捕捉入水信息难度大，因此针对高速入水空泡研究大多数采用数值模拟的方法，一方面可节约试验成本，另一方面可对高速入水空泡流场进行更加精确、更加全面的信息捕捉与流场分析。在数值模拟方面，苗圃等[10]数值模拟分析了圆柱体入水过程的空泡发展、压力演化和速度衰减过程，施红辉等[11]基于有限体积法建立了两连发高速航行体入水计算模型，并对其入水过程的超空泡演化规律和超空泡压力场变化情况进行了计算分析。利用机理研究的方法可对高速航行体入水过程快速建模，对理想入水环境下的空泡发展情况进行快速预测。Lee等[12]利用能量守恒原理对航行体高速入水空泡演化特性进行了研究，建立了高速入水条件下的入水空泡动力学模型；Li等[13]基于准确的入水空泡形状预测模型，对带调节尾舵的超空泡航行体入水过程的空泡发展与入水机动特性进行了研究，揭示了尾舵触水的非同步性对入水航行体机动的影响机理。

航行体高速入水过程中的强流固耦合特性会增加航行体发生大变形及破坏的可能性，计及入水过程中的流固耦合现象研究更有利于真实、深入地理解高速入水过程。由于流固耦合实验不仅要考虑入水流场的演化捕捉，而且针对结构应力应变需要构建有效的测量方法，这极大增加了实验的设计与执行难度，因此高速入水航行体流固耦合研究也往往采用数值模拟方法。Brooks和Anderson[14]基于Ls-dyna平台采用任意拉格朗日-欧拉（arbitrary Lagrangian-Eulerian,ALE）算法开展了返回舱入水过程的模拟计算，期间利用Gruneisen状态方程和流体的压力密度等关系式，采用无反射边界来对无限水域进行模拟，最终得到了与试验数据吻合较好的计算结果。Feng等[15]通过ALE方法开展了固定翼飞机入水仿真工作，具体研究了飞机初始姿态角对入水加速度变化以及压力场分布的影响。Li等[16]采用ALE算法并结合罚函数耦合的方式计算并总结了缓冲罩壳在结构体入水过程中对流场及载荷的影响规律。魏英杰等[17]采用实验与数值模拟相结合的方法研究发现超弹性球体入水后局部绕流与球体变形导致超弹性球体的表面压力变化范围要比刚性球体大。范旭东等[18]基于ALE方法研究发现入水冲击载荷大小和空泡轮廓尺寸均与航行体空化器尺寸成正比。于佳晖等[19]采用ALE方法建立了锥形头部圆柱入水流固耦合仿真模型，并利用分段刚体计算截面载荷的方法研究了初始入水速度对航行体入水冲击加速度、速度、位移和截面载荷的影响规律。

与传统高速入水问题研究相比，极地碎冰分布环境下的航行体高速入水过程研究引入了航行体-流体-海冰之间的复杂耦合关系，这对航行体高速入水过程的研究带来了更大挑战。Ren 和Zhao[20]开展了三维刚性球体穿越层冰入水的数值模拟，获得了球体撞击冰层的裂纹发展路径、空泡形态以及球体入水的运动特性。Cui等[21]开展了航行体穿越层冰入水的数值研究，分析了有无层冰的空泡演化形态，并得到了冰层厚度与航行体砰击载荷之间的规律。闫雪璞[22]结合试验与双向流固耦合算法对浮冰扰动下航行体入水空泡演化、倾斜入水、流场发展特性与结构动力学特性等方面进行了研究。汪春辉等[6]采用S-ALE方法进行了圆柱体垂直破冰出水过程的数值研究，通过采用弹塑性应变率表征冰材料力学参数，并与试验结果验证得到一致的破坏效果，为极地入水航行体强度及优化设计提供了研究基础。

综上所述，国内外学者针对航行体入水空泡流场、入水流固耦合以及冰环境入水等方面均开展了大量研究工作，但由于高速入水流场扰动剧烈，入水空泡非线性显著，碎冰环境下航行体高速入水的同时与浮冰发生碰撞所带来的耦合效应复杂，因此针对高速航行体跨介质入水空泡流动以及航行体-流体-碎冰耦合作用机制等问题在研究手段以及分析方法上还需要进一步挖掘。本文针对碎冰环境下航行体高速入水过程开展了相关数值仿真研究，在方法上基于ALE算法创新性地构建了模拟实冰破碎过程的航行体高速入水计算模型，并针对碎冰群以及碎冰群间隙对航行体入水过程流场、动力学参数及其载荷的影响展开研究。本文研究结果进一步揭示了碎冰环境下高速入水过程流固耦合作用机制，为极地跨介质航行体研究提供了技术储备。

1 计算方法理论基础

1.1 控制方程

ALE方法综合了拉格朗日法与欧拉法的优点，结构体的边界追踪采用拉格朗日法进行捕捉，内部网格划分则采用欧拉方法。流动控制方程主要由质量、动量及能量守恒方程组成，本文ALE算法通过Lsdyna平台实现。

质量守恒方程：

动量守恒方程：

能量守恒方程：

其中：ρ为流体的密度；vi为物质速度；wi为物质速度与参照坐标的相对速度，常为对流项；xi为欧拉坐标；bi为作用于流体的体积力；E为总能比；i、j分别为网格坐标。应力张量 σij表达式为：

其中，p为压力，δij为克罗内克函数，μ为动力黏度。

1.2 接触算法

对于显式有限元计算，由于结构对流体的冲击而产生界面力，而这种接触力作用于流体及结构体网格节点，为了防止节点在界面间发生大穿透，在接触计算中通过指定相应的主面及从面对接触表面进行区分，并通过罚函数约束方法对从节点施加阻力，使穿透的节点以反方向作用，从而与主节点平衡。施加阻力Fs的表示公式为：

式中：d为渗透矢量；k为弹簧刚度，由主材料的体积模量K确定；χf为界面刚度的比例因子，取值范围为[0,1]；A为主面分段的面积；V为主面网格单元的体积。

1.3 流体状态方程

由于流体在受到结构体砰击后会发生较大变形，本文采用关键字*MAT_NULL对流体的黏性应力本构关系进行表达，通过状态方程对流体的压力及密度的关系进行表征。本文计算水介质采用Mie-Gruneisen状态方程，其关系式为：

其中： ρ0为材料初始密度；c为水中声速； µw为水的体积变化率；α为Gruneisen系数 γ0的一阶修正值；S1、S2、S3分别为冲击波速度与流体质点速度关系曲线的斜率无量纲系数；E0为初始材料内能。计算采用关键字*EOS_GRUNEISEN进行设置，具体参数见表1。

表1 水介质状态方程参数Table 1 Parameter of Water Medium State Equation

空气介质则采用线性状态方程liner-polynomial进行设置，状态方程压力公式为：

其中， µa为空气的体积变化率；Ci为线性多项式系数，对于空气介质，设置参数为C3=C4=0.4，其余多项式系数为0；E0为初始体积内能，设置为2.533×105。

2 数值方法验证与计算模型设置

2.1 ALE数值方法验证

为了验证ALE算法在高速入水问题上的有效性，结合已开展的高速入水试验进行数值验证。试验航行体模型为直径D= 0.12 m、长度L= 0.51 m的铝合金圆头空心体，模型等效密度为1237 kg/m3，总质量为5.35 kg。采用加压方式为航行体提供加速度并通过双束激光间隔测量入水瞬时速度，入水速度v0=64.83 m/s，6400帧/s高速相机对试验图像进行采集，模型内部布置加速度传感器。数值计算模型与试验条件保持一致，模型网格数共800万。

图1中数值计算所得到的入水空泡发展演化情况与试验情况相似，表明本文建立的高速入水数值计算方法可以有效地对航行体高速入水空泡形态与发展过程进行模拟捕捉。

图1 入水空泡形态对比Fig.1 Comparison of water entry cavity shape

图2为航行体加速度计算结果与实验结果的对比验证，撞水瞬间计算得到的加速度峰值为380g，与试验结果385g接近，在整个加速度变化时间内误差小于10%，进一步验证了本文数值方法的有效性与准确性。

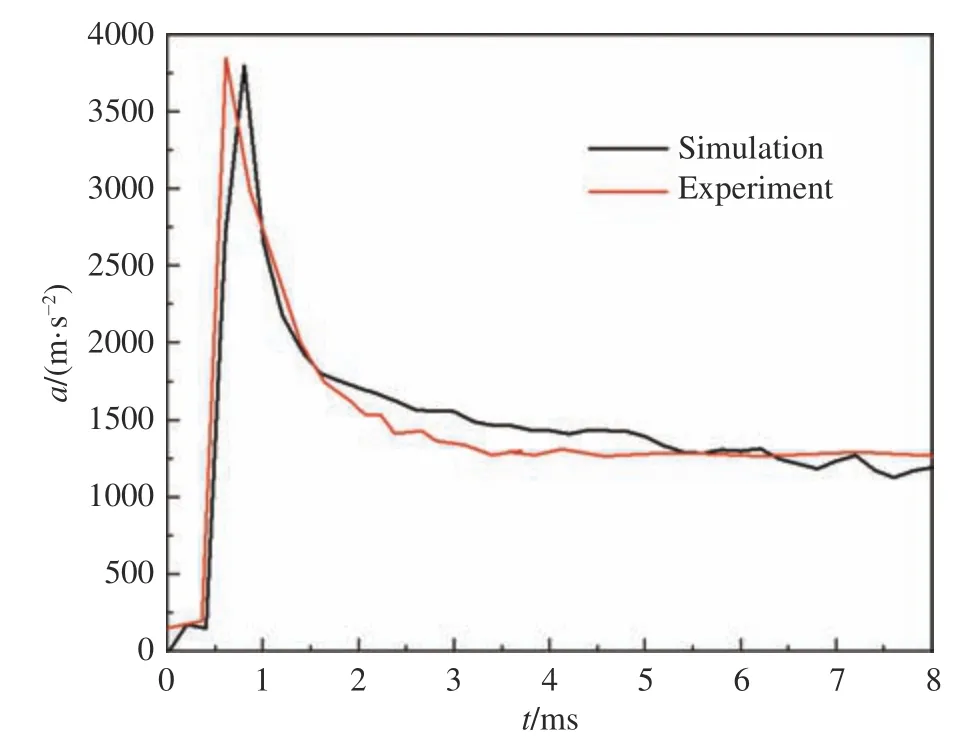
图2 入水加速度对比Fig.2 Comparison of water entry acceleration

2.2 冰材料模型验证

航行体高速入水过程中与液面浮冰发生碰撞，浮冰体受到碰撞将发生断裂破碎。为了更好地模拟浮冰破碎过程，需要构建浮冰材料模型，并对冰材料模型的破坏过程进行有效性验证，本文参考冯炎和李辉[23]所做冰材料的三点弯曲试验开展冰材料性能的验证工作。试验中冰材料为0.65 m（长）×0.07 m（宽）×0.07 m（高）的长方体，图3（a）给出了三点弯曲试验的原理及试验结果图像，该试验主要通过在底部对称布置两个承载点，并在中部施加载荷p，记录加载物的位移载荷曲线以及冰材料的破坏状态。压力施加采用缓慢增速方式实现，因此忽略材料的动态效应。数值验证模型采用本构材料ISOTROPIC_ELASTIC_FAILURE规定的一种简单塑性应变非迭代塑性破坏模型，该模型在模拟冰体裂纹产生与扩展方面具有较好的效果。模型尺寸与试验一致，布置方式与网格划分情况如图3（b）所示，所采用的冰材料参数[24]如表2所示。

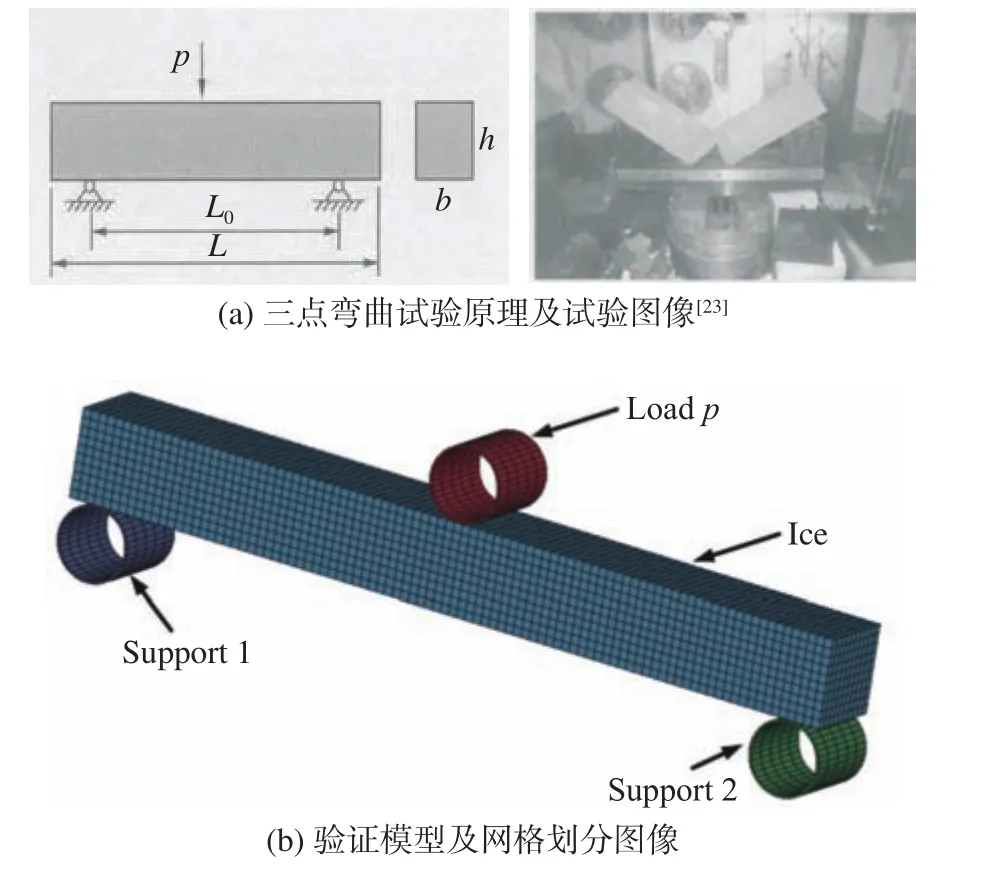
图3 三点弯曲试验与数值模型图Fig.3 Three-point bending test and numerical model diagram

表2 冰材料参数[24]Table 2 Material parameters of ice[24]

图4给出了数值计算和试验测量的加载物体位移与所受载荷的关系曲线，发现载荷峰值出现的位移相近，且加载物体发生相同位移时对应的载荷峰值误差小于5%。图5给出了三点弯曲数值模拟过程中冰材料受力的应力云图以及开裂趋势，可以观察到，开裂位置由底部中心点开始，同时断裂时间十分短暂，裂纹同时向上迅速发展，整个冰梁结构断裂为两段，这与图3（a）记录的冰断裂试验结果相近，因而验证了本文数值冰材料的有效性。

图4 数值与试验载荷位移曲线对比Fig.4 Comparison of load-displacement curves between numerical and experimental results

图5 冰材料加载破坏过程应力云图Fig.5 Stress contour during the loading and failure process of the ice material

2.3 计算模型及设置

本文计算航行体采用MK54简化模型，其具体尺寸如图6所示，模型总长度L= 2.7 m，圆柱段直径D= 0.324 m，头部截面直径D1= 0.2 m，尾部端面直径D2= 0.1 m。采用等效密度计算，模型总质量为240 kg。

图6 航行体几何模型Fig.6 Vehicle geometry model

航行体采用六面体进行网格划分，网格基础尺寸为0.01 m，对航行体头部及尾部过渡段进行局部加密以保证耦合效果；流域采用圆柱体几何建模，为消除边界效应，流域直径尺寸为航行体圆柱段直径的16倍，长度则为航行体模型总长度的5倍，同样采用六面体网格，并对水面以及航行体运动轨迹区域进行网格加密，水面处网格尺寸与航行体尺寸相同，共绘制820万网格，网格划分情况与坐标系定义方法如图7所示，其中定义重力方向为坐标系z轴负向。

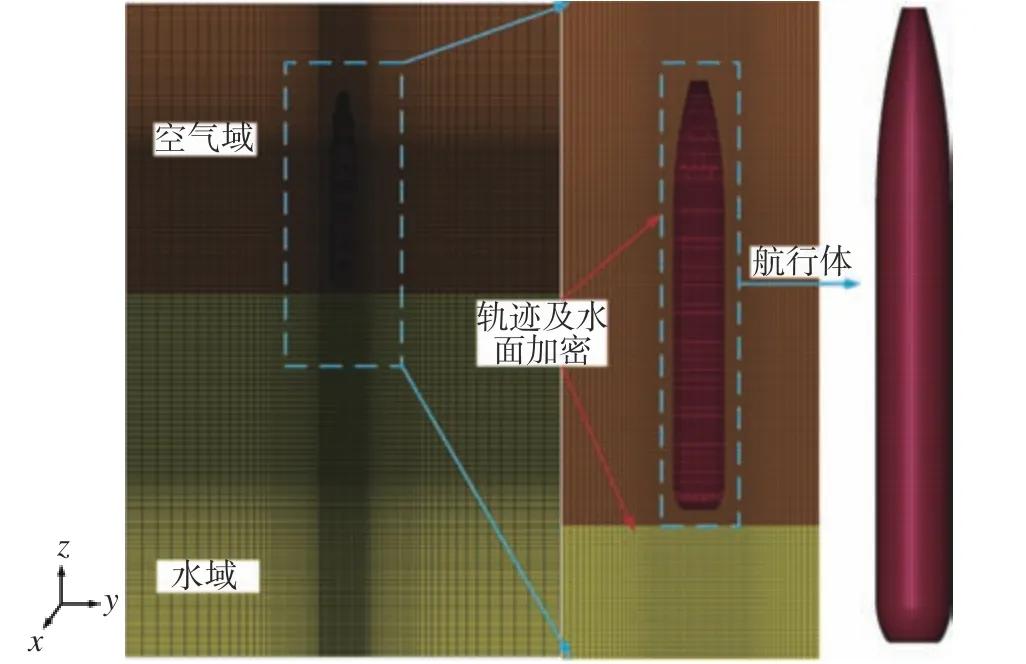
图7 计算域及航行体模型网格划分Fig.7 Gridding of computational domain and vehicle model

碎冰采用长方体几何建模，单块碎冰尺寸为0.1 m（长）×0.1 m（宽）×0.05 m（高），构成正方形碎冰群9（行）×9（列），每两个碎冰块之间的间隙为0.02 m，且布置结构体落点位于碎冰群的正中心。为保证结构体碰撞耦合形式良好，碎冰网格同样采用六面体网格进行划分，网格尺寸为0.01 m，网格划分形式如图8所示。由于自然环境中冰层悬浮于水面环境，因此为保证初始碎冰的悬浮状态，考虑浮力与重力相平衡，在计算初始化过程中将浮冰90%体积置于水面以下。航行体初始头部位置到碎冰群上表面的垂直距离为0.2 m，初始速度为100 m/s。

图8 碎冰群几何结构及网格划分Fig.8 Geometric structure and grid division of ice group

3 结果与讨论

3.1 碎冰环境入水流场演化特性

碎冰环境下航行体高速入水过程中，航行体-流体-碎冰耦合过程复杂，本文首先在无冰环境下针对入水过程中的空泡流场演化开展研究。图9（a）为航行体入水过程中的空泡演化情况。航行体头部入水后，自身夹带的空气也进入水中并向两侧排开流体形成初始入水空泡，随着航行体入水深度的不断增加，入水空泡体积随着空泡的扩张也逐渐增加。当t= 32 ms后，航行体完全处于水线以下，水面发生抬升，在静压以及空泡切向速度共同作用下，空泡逐渐闭合至一点，形成空泡表面闭合，且在闭合后水面上方观察到明显的射流现象；t= 40 ms时刻可以观察到两股反向的射流分别向空泡内部以及空中冲击。

图9 航行体入水空泡演化Fig.9 Water entry cavity evolution of vehicle

图9（b）给出了航行体穿越碎冰环境过程中入水空泡的演化情况。航行体初始撞击水面浮冰，使撞击部位的浮冰发生破坏并被迫挤压向下运动。空泡发展过程中（t= 8～24 ms），一部分碎屑冲击至气水界面并随着空泡壁一起运动，其中部分碎冰伴随着飞溅冠的运动向空气中溅起。未直接受到模型冲击的碎冰在水面抬升的影响下向上隆起，并在水平方向上随流体发生一定程度的移动。t= 32 ms时，由于静水压力与空泡壁面黏性力相平衡，入水空泡形成表面闭合，空泡上表面表现为收缩状，碎冰随之向中心位置收缩，部分碎屑在射流影响下进入空泡内部。

通过对比有无碎冰情况下航行体入水空泡形态可以发现，碎冰环境入水初始阶段，空泡壁面会出现界面波动，如图9（b）中t= 8 ms的空泡图像所示。碎冰环境下的初始开空泡是由于碎冰受到航行体的挤压而产生的，航行体与水面之间的初始间隙由冰层占据，当冰层发生破碎失效且侧向滑移时，水面下沉速度较小，因此航行体与水面的间隙逐渐消失并产生直接接触，航行体的直接触水使得入水空泡进入了新的扩张阶段，其扩张空泡与原有的空泡初生壁面相交融，从而形成了不光滑带有拐点的空泡波动壁面。在靠近水面的部分空泡壁面上可以观察到部分冰碎屑在整个时间历程的附着现象，这说明了空泡壁面具有流动特性，如图中虚线所示。碎冰屑垂直方向抬升轨迹与时间近乎成正比，因而呈现随空泡壁匀速抬升运动的现象，同样在水平方向上碎冰屑随空泡壁面产生了扩张或者收缩的运动响应。

在飞溅冠的发展上，碎冰明显对水面的抬升起到了抑制作用。碎冰环境的飞溅为冰水混合物，且在发展趋势上明显受到水面上其余未被破坏冰层的影响，在水面抬升高度以及飞溅的收缩性上受到明显阻碍作用。t= 40 ms时无碎冰环境下入水空泡表面闭合形成，并产生了向上及向空泡内部的明显射流现象。无冰环境泡内射流的冲击速度高于航行体且具有较大的冲击载荷，而在碎冰环境中，射流现象并不明显，但存在碎冰屑的泡内下落，这表明碎冰通过延缓飞溅冠的演化、表面闭合时间以及闭合状态，对泡内压力变化产生了影响。

图10给出了碎冰环境航行体入水过程中流体的速度场演化过程。观察水面与航行体头部接触位置速度可以发现，t= 4 ms时存在明显的流场加速过程，此时最大流场速度达到105 m/s。随着航行体入水深度不断增加，动能逐步转换为流体的变形能，头部端面流体峰值速度开始降低，对比4～12 ms时的空泡尺度，发现在航行体同一垂直位置处空泡尺度基本相同，且其速度场范围也基本相近，这与空泡独立膨胀原理相一致。在t= 12 ms后，空泡壁面的流动速度呈现不均匀式分布特点，越靠近水面其速度越低，较大的速度主要集中在航行体头部附近，从航行体头部至肩部，速度由90 m/s减小到30 m/s，而在肩部至水面范围内速度则在0～30 m/s之间，且该趋势随入水深度增加未发生变化。在飞溅演化上，在飞溅冠形成发展期间（t= 12～28 ms），可以观察到飞溅冠的速度随着高度增加而增加，即飞溅越远离水面，其速度越快，因而飞溅的连续性难以维持，呈现出扩张、离散形式的发展规律。

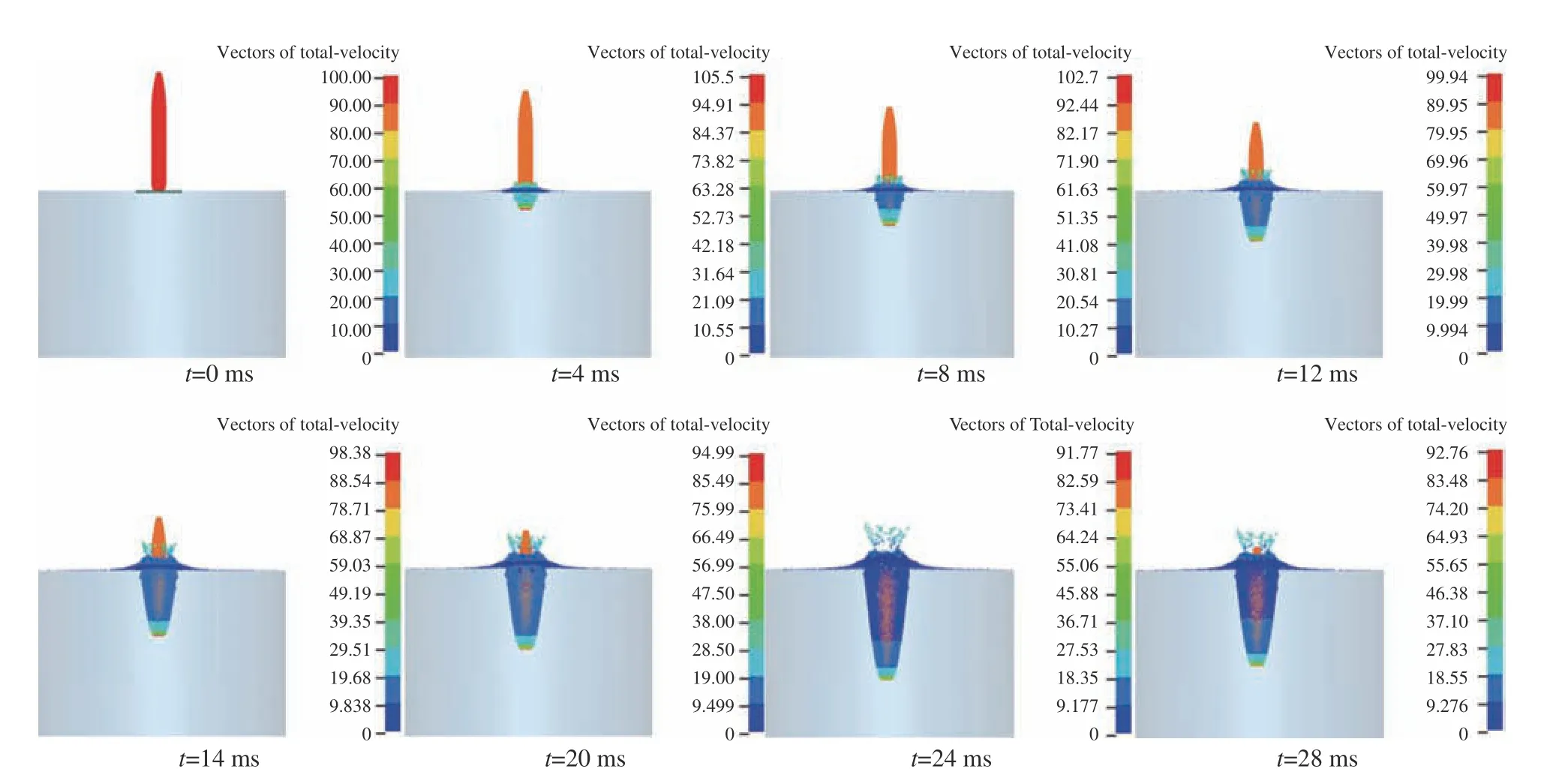
图10 碎冰环境航行体入水速度场演化Fig.10 Velocity field evolution of water entry of the vehicle in the fragmented ice environment

图11给出了t= 36 ms时航行体在有无碎冰环境下的流场速度云图对比。对比发现碎冰的存在一方面抑制了水面抬升速度，另一方面航行体撞击产生的飞溅水质点会携带冰碎屑向上运动。由于冰的密度小于水，在相同动能条件下会具有更大的运动速度，因此碎冰环境高速飞溅分布范围大于无碎冰环境。有无碎冰环境入水空泡壁面上的速度分布同样存在着差异性，虽然撞击冰面后航行体所具有的速度较小，但在头部速度分布上， 20～90 m/s区间，撞冰入水的空泡壁面分布区域更大。在碎冰环境下观察到空泡内部的溅落物运动速度高于无冰环境，溅落速度最大可达到100 m/s，超过了航行体的运动速度，后续会撞击航行体或者空泡壁面形成扰动。

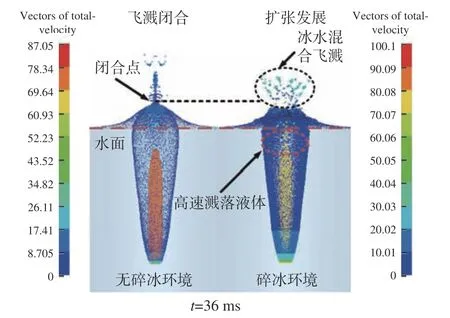
图11 有无碎冰环境流场速度云图对比（t = 36 ms）Fig.11 Comparison of velocity contour with and without the fragmented ice environment (t = 36 ms)

3.2 碎冰冲击破坏特性

航行体高速冲击浮冰冰块，整个过程局部浮冰发生明显的运动与破坏，碎冰冲击破坏特性直接影响入水流场演化过程及其入水航行体动力学特性。通过提取入水的俯视图可以观察到碎冰群的破坏形式，图12为整个入水时间历程内碎冰破坏应力的发展云图，整个冲击发展历程分为模型冲击破碎、冰层挤压破碎、冰块翻转破碎以及收缩破碎等4个阶段。冲击破碎阶段主要是由于模型与冰层的直接接触载荷超过冰层强度而产生的，一般发生在航行体刚开始撞击冰面时刻，即为图12中t= 0～8 ms期间。冰层挤压破碎的直接诱因是入水所激起的不均衡水面抬升现象，在水面抬升过程中，抬升高度以撞水点为中心，随着远离撞水点而降低，因此，靠近中心部位的冰层在抬升后由于重力以及波纹传播的影响向四周的冰块靠近并发生碰撞挤压，该过程主要发生在t= 8～24 ms期间。冰块翻转以及收缩过程的破碎则是由水质点的砰击所导致的，如t= 24～32 ms期间，冰块在受到挤压之后开始产生翻转，进而产生翻转碰撞破碎，当受到影响的冰块翻转结束再次落水；t= 32～40 ms期间，入水空泡慢慢闭合溃灭，周围的碎冰向空泡中心不断聚集，此时碎冰破碎主要由于向空泡中心运动过程中碰撞产生的，即收缩破碎阶段。在大气压力以及静水压力联合作用下，空泡壁面收缩逐步形成闭合，此时水质点的运动速度较大，会在一定程度上对冰块产生冲击从而发生破碎现象，但相较于上述模型碰撞以及冰层挤压，这种破碎的范围较小，破碎程度较弱。

图12 碎冰砰击破坏过程演化Fig.12 Evolution of fragmented ice destruction process

在碎冰群整体演化趋势上，如图12所示，航行体冲击瞬间的冲击孔隙与航行体头型相一致，而在应力传递后与模型直接接触的中间9个冰块最先发生完全破碎，此时的孔隙如图12中t= 8 ms图像所示，其孔隙形式上为方形扩张。值得注意的是方形孔隙形状特点与碎冰的排布方式有直接关系，因为在t= 16 ms左右，碎冰扩张的轮廓呈现为圆形，这表明方形孔隙的产生是由于应力传播过程中顶角位置所受的阻力与上下左右四个方向相比较大，其冰层破坏扩张速率表现出了差异性。随着入水空泡发展至表面闭合，碎冰在水面流体质点向内收缩流动的驱动下向内收缩，并发生了向中心位置的转动，碎冰之间的间隙再次增大。在碎冰形成扩张趋势到收缩的整个过程中，碎冰区域有效应力变化较小，均维持在4 MPa左右，即水质点流动过程的破碎效果较弱，冰的破碎主要是航行体冲击以及冰层间的挤压所造成的。

图13提取了冰层破碎初始时刻的演化情况。为方便说明，对中心位置9块碎冰进行编号，如t= 0 ms时刻图像所示。在t= 0.2 ms时，模型与冰层未完全接触，此时的应力主要是模型头部的气垫效应所导致的。气垫效应之所以产生，是因为本文计算采用的航行体头部为平头结构，且航行体入水速度极高，在入水之前，航行体头部区域就驻留了大量的气团，气团聚集起来形成了高速气垫。与冰块最先接触的高速气垫直接拍击冰面，导致了冰面上的应力呈现出与航行体头部形状类似的圆环状分布形式，有效应力最大值分布在碎冰模型中心位置，且应力随着远离中心而降低，峰值有效应力为0.35 MPa。特别的，可在2、4、6、8号碎冰块边线上观察到应力集中现象。t= 0.4 ms时，模型与冰层发生接触碰撞，最先接触为模型头部平面，此时在冰层表面表现为均匀的高压分布，有效应力值为0.168 GPa。随着航行体模型的进一步运动，模型推动冰体发生下陷，且在模型头部轮廓边缘与冰结构交接处出现了应力集中，此时最大有效应力进一步增加至0.18 GPa，其受力远超过冰材料的强度，进而t= 0.8 ms时层冰发生了碎裂现象。可以明显看出，1、3、7、9号碎冰块仅在模型接触的一角发生了较为明显的碎裂现象，并出现应力的传递，在t= 1.0 ms时完全破碎。在这个过程中，冰层表面的应力随破坏脱离航行体的进行而减小，在内部9个冰块完全破碎时最大有效应力降低至20 MPa。

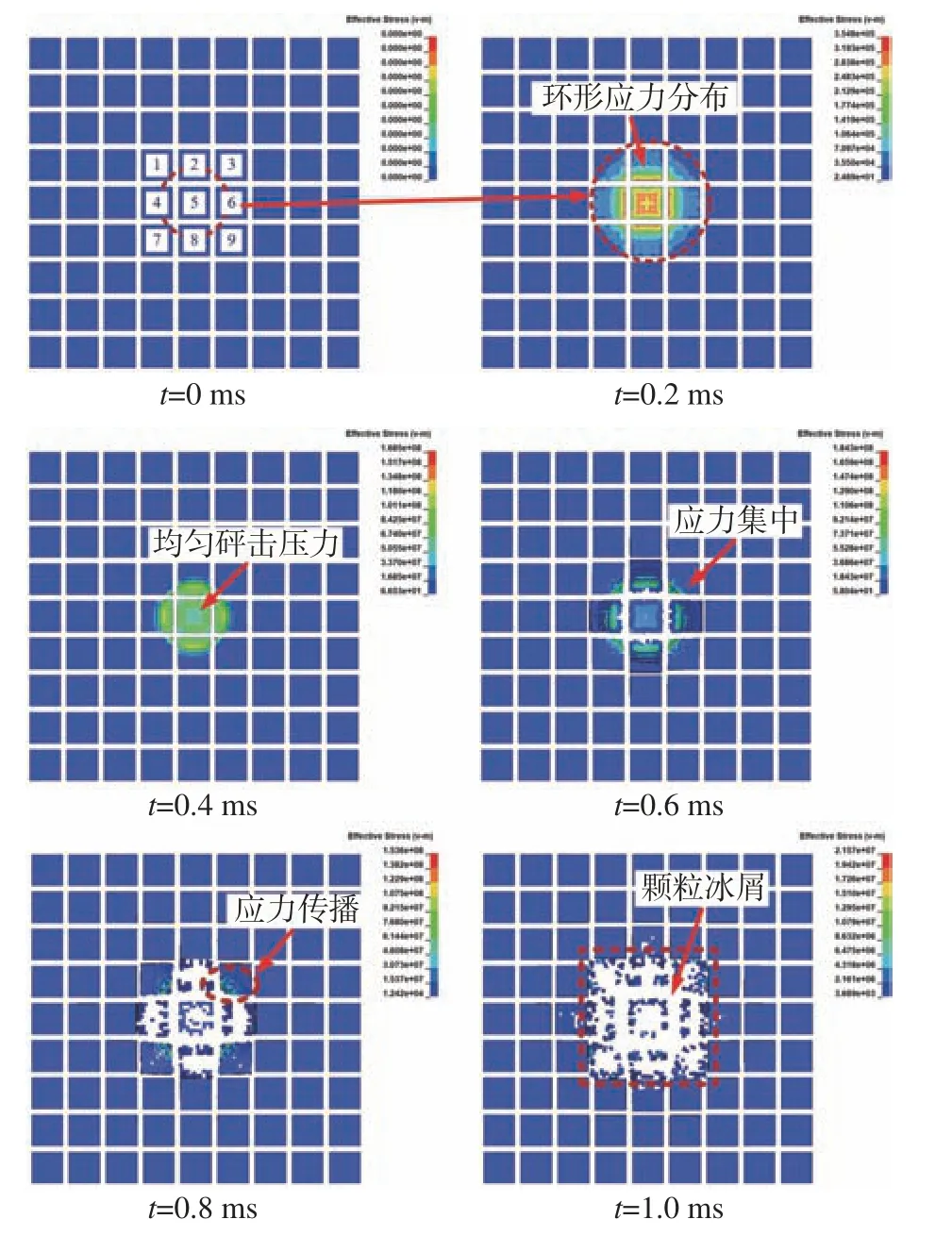
图13 入水早期碎冰破坏应力云图Fig.13 Stress cloud map of fragmented ice failure in the early stage of water entry

3.3 碎冰环境入水运动特性研究

由于航行体初始撞击物质材料属性差异，航行体撞击产生的冲击载荷以及运动特性也会存在差异。图14为有无碎冰环境下航行体入水过程运动特性参数曲线。无冰环境中，航行体撞水瞬间加速度峰值为700g，而碎冰环境下入水加速度峰值可达到1325g，两种环境下的加速度峰值脉宽基本相同。加速度峰值出现后，碎冰逐渐消失，航行体与水面发生拍击并产生了局部加速度峰值。由于流体初始阶段的加速运动以及航行体撞冰发生的动能转换和能量损耗，二次砰击加速度峰值远低于第一次砰击加速度，峰值仅为187g，所以碎冰的存在一定程度上减小了航行体撞击水面的二次冲击载荷。

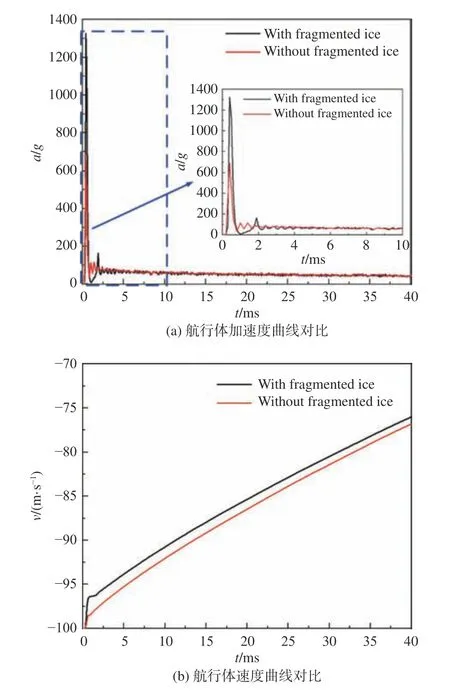
图14 不同入水环境航行体运动特性参数曲线Fig.14 Parameter curves of vehicle motion characteristics in different water entry environments

碎冰环境入水时，航行体的部分能量被碎冰的变形破坏过程所吸收，因而在速度曲线上表现为明显的瞬时拐点，且碎冰环境具有更大的速度损耗。两种入水环境下航行体加速度曲线变化趋势基本一致，因此在速度的降低趋势上同样表现出一致性，仅在数值大小上存在差异。

3.4 碎冰间隙影响研究

北极海域地区除了被厚度较大的层冰覆盖外，还存在以散碎浮冰形式覆盖的海冰水域，这些水域往往更适合高速航行体入水发射。碎冰覆盖海域浮冰块之间存在一定的海冰间隙，因此针对海冰间隙展开入水研究具有实际应用价值。本文针对碎冰分布的间隙大小开展参数化研究，探究碎冰间隙对入水流场及载荷的影响规律。碎冰间隙r选取方式为：当r= 0.05 m时，航行体触水时头部与相邻冰块正好相切，以此为基准，分别向内、向外变化0.03 m，对应r= 0.02 m工况与r= 0.08 m工况，具体如图15所示。碎冰网格划分方式同图8，航行体入水速度为100 m/s。

图15 碎冰间隙示意Fig.15 Schematic of fragmentated ice gap

图16和图17分别为航行体在r= 0.05、0.08 m时的入水空泡演化情况。对比图9（b）不难发现，在水面抬升程度上，碎冰间隙的影响并不明显，而飞溅冠生成过程中，大碎冰间隙入水时所形成的飞溅中夹带有较大块冰屑，且飞溅冠形成的水流稳定程度与碎冰间隙呈现出正相关性。在水下空泡形态发展及空泡尺度上，不同碎冰间隙的差异性并不明显，空泡发展皆较为完全，空泡演化连续；而初始撞击产生的碎冰在空泡壁面附着产生的空泡扰动则具有随机性，在较大碎冰间隙入水时，空泡壁面的附着量明显降低，且影响相对较小。因而，碎冰间隙对空泡演化的影响主要集中在飞溅冠的演化，以及碎冰屑的附着量上。

图16 碎冰间隙r = 0.05 m时的入水空泡演化Fig.16 Evolution of water entry cavity for ice gap of r = 0.05 m

图17 碎冰间隙为r = 0.08 m时的入水空泡演化Fig.17 Evolution of water entry cavity for ice gap of r = 0.08 m

t= 40 ms时不同间隙尺寸条件下的入水流场速度如图18所示。对比3种工况可以发现，在水下空泡壁面速度场分布上三者差异较小，在航行体头部位置空泡壁面运动速度达到72 m/s，且空泡壁面不同速度区域过渡明显，仅在靠近航行体头部区域具有较大速度，整体空泡速度多分布于0～20 m/s区间。在飞溅演化上，可以明显观察到在r= 0.02 m时具有更大速度的飞溅发展，且在飞溅物的连续性上较差。这主要是由于在碎冰间隙较小时，初始碰撞产生的碎屑夹带在飞溅液滴中向上运动，由于混合发展，飞溅冠的连续性受到破坏，而间隙增大时，碎屑体积相对减小，水面抬升作用于整块碎冰，因此可以在r= 0.05、0.08 m时的飞溅中观察到较为完整的冰块，飞溅则主要由水质点组成，因而在连续性上得到改善。同时，可以注意到随着间隙的增加，飞溅的闭合时间也将提前。在闭合形成的射流方面，随着碎冰间隙增大，射流的峰值速度将会降低，因此后续运动中对模型的冲击干扰也将得到减缓。

图18 不同碎冰间隙入水流场速度云图（t = 40 ms）Fig.18 Velocity contour of water entry flow field of vehicle at different ice gaps (t = 40 ms)

图19为不同碎冰间隙条件下入水初期冰层破碎过程的有效应力云图。在破碎形态上，在间隙较小时，航行体与冰层的初始作用面积存在一定的区别。由于航行体头部端面直径为0.2 m，因此在r= 0.02 m时，初始撞击会接触以中心点为圆心四周共9块碎冰，但对角方向的冰块接触面积较小，因此在破坏程度上较轻。随着间隙增加，航行体撞冰初始接触面积降低，因此初始破碎冰块的数量逐渐减少：在r= 0.05 m时为中心及上下左右5块，而在r= 0.08 m时，可以观察到破碎主要集中在中心冰块。

图19 碎冰冲击破坏初期有效应力云图Fig.19 Effective stress contour at the initial stage of ice fragmentation impact failure

在应力分布上，由于冰块形状为正方形，因此在碰撞挤压过程中冰块的边界处易发生应力集中现象。对比发现应力峰值大小随着间隙的增大而降低：在t= 0.4 ms时，r= 0.02 m的峰值应力达到168 MPa，而在r= 0.05、0.08 m时相对应的应力峰值则为135、81.5 MPa。随着破碎发展，应力峰值逐渐降低，而在小间隙时模型与碎冰的接触面积大，其航行体所受阻碍持续时间长，应力仍维持在较大程度，在大间隙时则具有较为明显的应力衰减情况。

图20为航行体模型在不同碎冰间隙下入水的运动特性参数曲线，从中可以得到碎冰间隙对航行体整体冲击载荷的影响规律。通过对比撞击瞬间加速度峰值可以发现，随着间隙的增加，撞击加速度峰值呈现减小的趋势。r= 0.05 m时加速度峰值由r= 0.02 m时的1300g降低至950g。但值得注意的是，在r=0.05、0.08 m时的加速度峰值差距较小，这主要是由于瞬时冲击加速度主要和航行体与冰层的接触面积有关，在间隙达到足够大时，碰撞接触面积基本稳定，因而加速度峰值变化较小。入水后航行体运动速度差别较小，但同样呈现出随着碎冰间隙增加而逐渐增加的趋势。

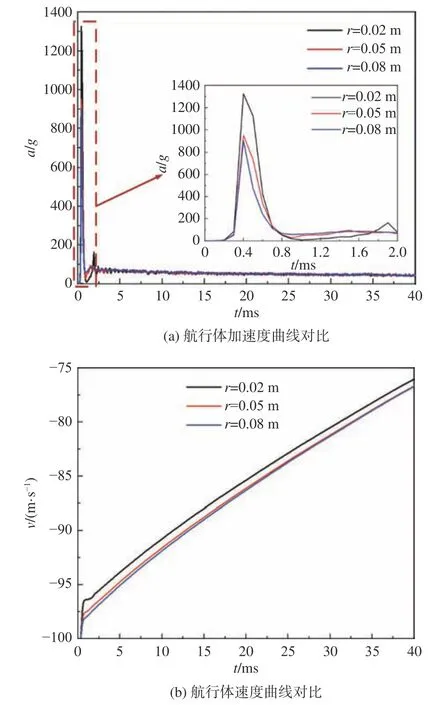
图20 不同碎冰间隙入水航行体运动特性参数曲线Fig.20 Parameter curves of water-entry vehicle motion characteristics in different ice gaps

4 结 论

本文针对漂浮碎冰环境下的航行体高速入水动力学问题展开研究，利用ALE算法建立了碎冰环境下航行体高速入水流固耦合计算模型，并对碎冰作用下的航行体高速入水流场、载荷特性以及不同碎冰间隙环境下的航行体入水特性进行了计算分析，针对碎冰不同的破坏原因进行了分类分析，将碎冰破坏发展过程归纳为不同的特征阶段。得到以下结论：

1） 在航行体入水空泡及流场的演化方面：碎冰的存在对航行体入水后的水面抬升以及产生的飞溅演化存在抑制作用；碎冰的破碎主要受到航行体砰击、冰层挤压以及水质点冲击等因素的影响，并且航行体砰击在冰块破碎中占主导作用，此外冰层破碎过程中存在圆形应力集中、方形扩张、圆形收缩等一系列具体发展特性。

2） 在航行体入水载荷方面：碎冰环境下航行体的入水冲击载荷显著增加，其过程相较于无冰环境具有更大的动能损耗，但其砰击载荷持续时间与无冰环境入水一致，航行体碎冰环境入水过程会产生两次砰击峰值，且第二次峰值远小于第一次。

3） 在碎冰间隙对飞溅冠演化及砰击载荷影响方面：飞溅冠的连续性随着间隙的增加而提高，冰层所具有的峰值应力随着间隙增加而减小，且破碎倾向集中发生于中心位置。在本文所取间隙范围内，航行体瞬时砰击载荷与间隙大小呈负相关关系，间隙足够大时，砰击载荷变化相对较小。

未来将基于本文开展的研究工作内容，进一步针对不同海冰环境下的弹性航行体高速入水过程进行研究，其中主要聚焦于不同的海冰几何模型与分布模型下的高速入水过程，以此达到更加真实地反映极地环境下航行体高速入水过程的目的，进一步提升研究的工程实际价值。