基于卷积神经网络的气动热预测方法

袁佳铖，宗文刚，*，曾 磊，李 强，张昊元，蔺佳哲

(1.四川大学 化学工程学院，成都 610065；2.中国空气动力研究与发展中心，绵阳 621000)

0 引 言

作为高超声速飞行器面临的主要挑战之一[1]，气动热防护一直是其设计工作的重点。在实际工程工作中，设计师们会对目标飞行器的气动热环境进行预测以辅助热防护设计，为了保证飞行器能够正常工作，通常会进行大量的冗余设计，这样虽然保证了飞行器的飞行安全，但也增加了成本和重量，严重制约了飞行器的性能。因此气动热环境预测的准确度与速度是飞行器性能与设计效率的关键。目前常用的飞行器气动热环境预测方法有3种，分别是工程计算方法、风洞试验和CFD数值模拟[2-4]。其中，随着计算机硬件技术的飞速发展，CFD数值模拟技术越来越成熟并逐渐成为获取大量气动热数据的主要手段之一。

在多年的研究与工程实践中，我们已经积累了大量的气动数据，如何对这些数据进行再利用，探索科学研究的“第四范式”，逐渐成为一个研究重点。在这一方面，美国已经开展了大量的研究，例如由NASA资助的XAI-DAV（eXplainable AI for Design of Aerial Vehicles）项目已经能够在短时间内从9000多个飞行器外形中筛选出最优秀的设计案例，并提供合理的设计依据，使设计方案更具可解释性和可靠性。

随着深度学习技术的快速发展，国内外许多学者尝试利用深度学习技术构建数据驱动的气动特性预测方法，并取得不少成果[5]。作为深度学习的关键技术之一，卷积神经网络（convolutional neural networks,CNN）[6]以其对空间信息出色的处理能力，赢得了众多学者的青睐。在航空航天领域，许多学者利用CNN开展了气动特性以及流场预测方面的工作，并取得了不错的效果[7-12]，但主要应用于二维流场。CNN在三维流场中应用并不广泛，主要原因是三维飞行器的几何特征难以提取，而且普通计算机难以处理大尺寸、高维度的张量。但是，如果只考虑三维外形表面的热流等问题，那么需要考虑的就只有飞行器的表面几何特征，因此将CNN应用于三维飞行器外形的气动热预测是可行的。

目前也有一些学者尝试利用机器学习方法建立了数据驱动的快速气动热预测方法。在不考虑飞行器外形因素的条件下，许多学者采用本征正交分解（proper orthogonal decomposition, POD）建立了气动热代理模型[13-15]，针对单个飞行器，以来流参数为输入，实现气动热的快速预测。采用类似的思路，张智超等[16]提出了一种基于径向基函数神经网络的气动热预测代理模型，该模型在飞行器表面的每个点上建立独立的网络来进行热流单独预测。除此之外，还有利用气动热与边界层外缘信息相关的特点，基于支持向量机建立了当地化的气动热快速预测方法[17]。这两种方法由于没有考虑外形对气动热分布的影响，因此无法做到不同外形飞行器在不同来流条件下的气动热预测。为了能够对大量气动数据进行有效地再利用，实现飞行器设计所需的气动热快速预测，建立能够预测不同外形飞行器气动热分布的模型是十分必要的。Li[18]采用深度学习技术根据飞行器的整体几何特征和局部几何特征实现了不同飞行器在不同来流条件下的气动热快速预测。该方法的思路是可行的，但其在建模前需要获取飞行器的多种几何特征，且其神经网络结构过于复杂，因此建模效率较低。

综上，本文以不同外形飞行器在不同飞行条件下的气动热快速预测为目标，采用对几何信息具有较强处理能力且模型参数更少的卷积神经网络，建立了气动热快速预测模型。采用CFD数值模拟方法建立了气动热数据集，并用不同的神经网络模型对不同外形飞行器的气动热进行了预测，探索了不同网络模型的预测能力。与其他类似方法不同，本文所提方法采用了大量卷积神经网络结构进行飞行器外形特征的提取和热流重构工作，这使得模型参数量变少而且能够通过GPU实现加速，大大提高了训练效率。

1 热流预测模型

本节首先提出了一种三维外形几何表达方法，然后依据该方法详细介绍了两种基于卷积神经网络的热流预测模型，整个热流预测流程如图1所示。

图1 建模流程Fig.1 Flowchart of the modeling process

1.1 几何表达方法

飞行器的外形对其表面的热流分布有着巨大影响，同一飞行器表面不同区域的热流值不同，不同飞行器也会因为外形差异而热流分布不同。因此，想要神经网络模型能够准确预测不同位置、不同飞行器的热流值，如何将飞行器的外形几何信息传递给神经网络是关键。符号距离函数（sign distance function, SDF）作为目前深度学习领域常用的一种几何表达方法，广泛应用在空气动力学建模领域，但基本上是针对二维几何外形的。本文依据SDF原理，针对典型飞行器外形，提出了一种可用于卷积神经网络的三维外形几何表示方法，该方法具体实施步骤如下：

1） 在飞行器表面建立大小为M×N的单块结构网格，M表示沿x轴顺时针旋转方向上的网格点数，N表示沿x轴从飞行器头部到尾部方向上的网格点数。钝锥的重构网格如图2所示，可以看出由于外形的原因，网格线在n=1处坍缩为一个奇点。飞行器的头部热流通常较高，因此头部也是气动热预测工作中的关键区域，在CFD模拟中常常会对头部网格进行加密从而实现关键位置热流的精确模拟。本方法在建立网格时可以调整网格分布从而实现对头部网格的加密。针对本文研究的4种外形，考虑对周向网格采用均匀分布，而对轴向网格则在头部采用等比分布，在尾部采用均匀分布。

图2 钝锥重构网格Fig.2 Reconstructed mesh of the blunt cone

2） 计算网格中的每一个点到x轴的距离Rm,n并进行归一化，可以获得一个含有三维曲面特征信息的矩阵，如式（1）所示，并且根据这个矩阵可以还原三维外形。与SDF函数类似，这样的矩阵也能够转化为图像并作为神经网络的输入。

3） 根据重构的网格，对CFD计算得到的物面热流数据进行插值，获得重构网格对应点位的热流值并组成热流值矩阵，如式（2）所示。由于重构网格中n=1的点都对应了网格前端的奇点，因此理论上这些点的预测热流值应该相等，但事实上神经网络的输出并不满足这个要求，所以需要对预测热流矩阵中该列的值求取平均值，以避免无意义的误差。

1.2 卷积神经网络

卷积神经网络是深度神经网络的一种，广泛用于处理图像等有序数据，与人工神经网络类似，卷积神经网络的灵感来自动物视觉皮层的组织结构[19-20]。卷积神经网络通常由卷积块和神经网络的一些通用层组成，其中卷积块是由卷积层和池化层组成的，作用是提取输入图像的特征。CNN最重要的组成部分之一是卷积层，其主要功能是使用卷积核对矩阵进行运算。图3给出了一个简单卷积层的计算过程，可以看出一个7×7的矩阵在经过卷积层的运算之后变成了5×5的矩阵。

图3 卷积层运算过程Fig.3 Operation process on the convolution layer

由于矩阵在经过卷积层的运算之后尺寸会发生变化，因此为了保持输出图像的尺寸，通常会在矩阵边缘填充零来消除卷积层对矩阵大小的影响。此外，输出矩阵还受到卷积运算步长和卷积核大小的影响，输出矩阵大小的具体计算方法如式（3）所示：

式中：Sout和Sin表示卷积层输出和输入的尺寸，Spadding表示边缘填充的层数，Skernelsize表示卷积核的尺寸，Sstride表示卷积运算步长。在此基础上，为了保持矩阵的尺寸，卷积层的运算转变为图4所示的过程。

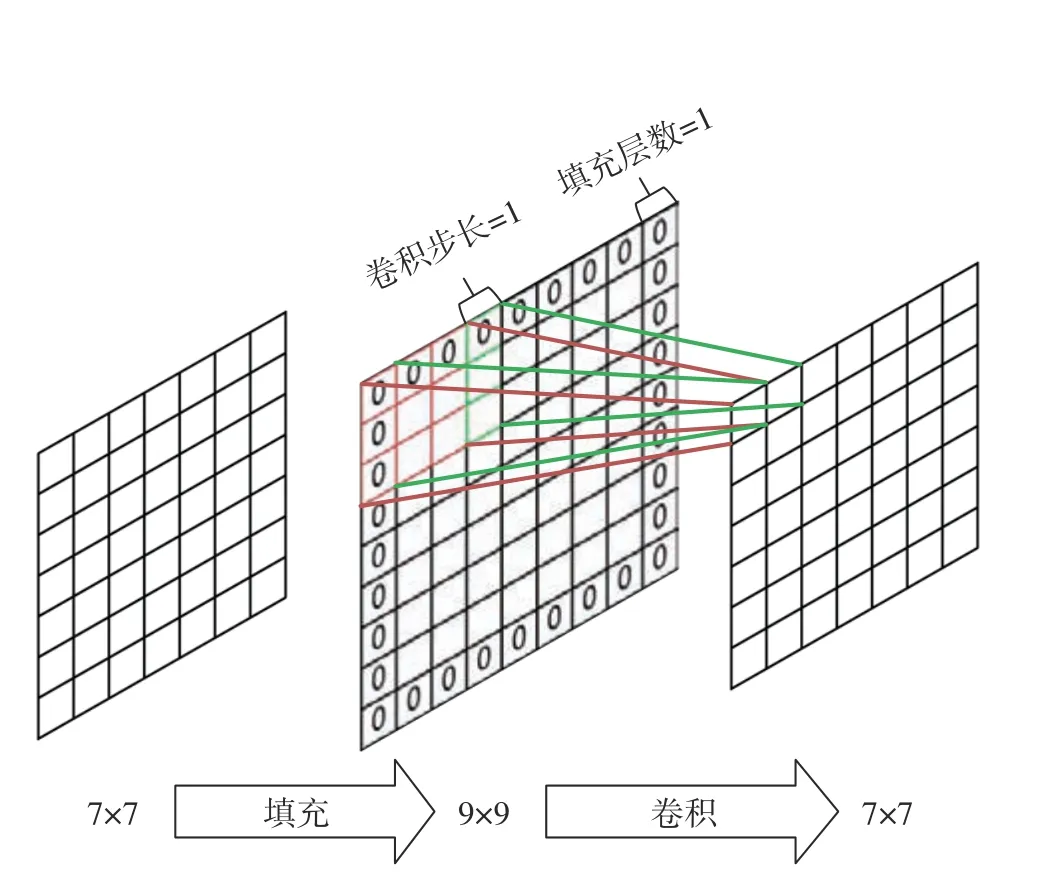
图4 带边缘填充的卷积层运算过程Fig.4 Operation process on the convolution layer with padding

目前卷积神经网络常用于图像识别和语义分割。针对图像识别的卷积神经网络通常是以图片为输入，以类别为输出，因此一般是由一系列的卷积块和一个全连接网络组合而成的。而语义分割的卷积神经网络是以图像为输出，因为需要根据卷积层提取出的特征对图像进行还原，所以其结构相对于前者来说更加复杂。本文采用类似语义分割的方法，以飞行器的外形特征矩阵和飞行条件为输入，对其表面热流进行重构，因此选用了通常用于语义分割的卷积神经网络结构。

1.3 网络结构

为了探索适用于热流预测的网络模型结构，本文分别基于传统卷积神经网络的编码器-解码器架构和全卷积神经网络（fully convolutional networks, FCN）的变体U-Net模型设计了两种热流预测模型。为了便于说明，分别用CNN模型和U-Net模型指代两种网络模型。

针对CNN模型，由于网络模型的输入不仅包括飞行器几何信息矩阵，还包括由飞行高度、马赫数和迎角组成的一维飞行状态向量。因此，有必要设计两个编码器来处理两种输入信息，然后通过一个全连接神经网络将两个编码器的输出进行融合并传递给热流解码器。整个神经网络由几何信息编码器、飞行条件编码器和热流解码器三部分组成，其整体结构如图5所示。其中几何信息编码器是由多个卷积层和池化层组成的一个卷积神经网络，其输入是二维的外形信息矩阵，输出是一个一维的向量，主要作用是对几何信息进行编码。来流条件编码器由多个全连接层构成，其输入是飞行高度（H）、马赫数（Ma）和迎角（α）组成的一维飞行条件向量，输出是一个一维向量，主要功能是将飞行条件编码为与几何信息编码器输出维度相同的向量。热流解码器结构相对较为复杂，其首先通过一个全连接神经网络对两个编码器的输出进行整合，然后通过卷积层和上采样层对热流矩阵进行重构，其输出是一个与几何信息矩阵尺寸相同的热流值矩阵。

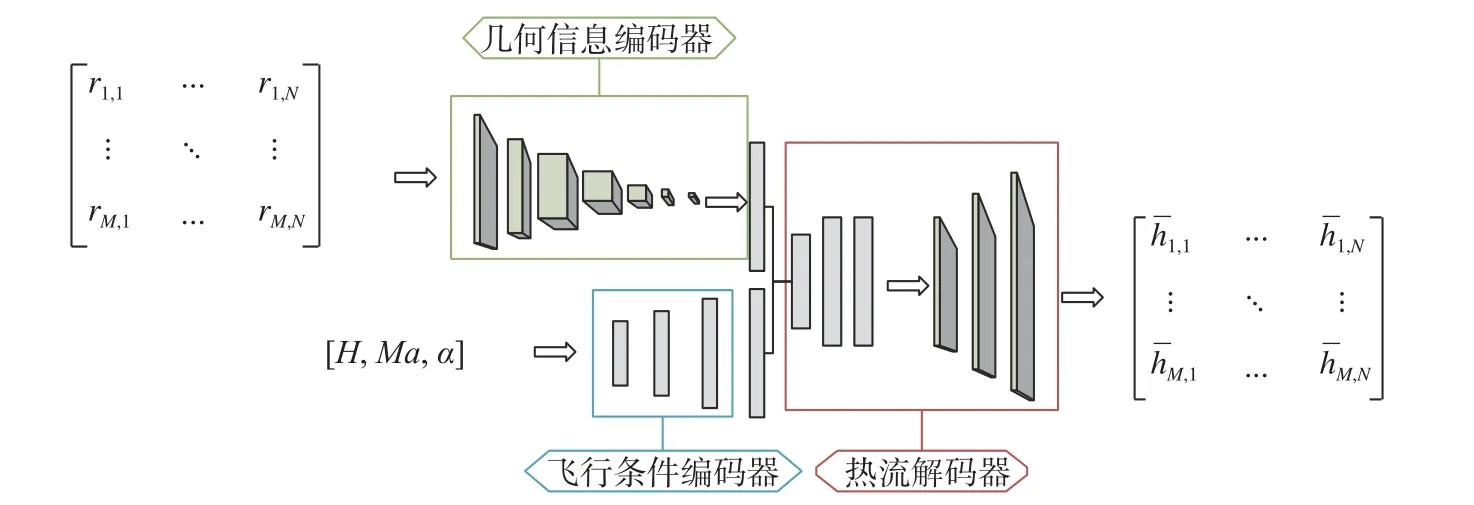
图5 CNN结构Fig.5 Structure of CNN

FCN是Long[21]于2015年提出的一种用于语义分割的神经网络模型，与传统CNN模型不同的是，该模型将全连接层全部替换为卷积层，使得整个神经网络完全是由卷积层、池化层和上采样层组成，这使得图像在神经网络运算传递过程中仅是分辨率发生了变化。U-Net作为FCN的一种，在提出时被用于医学图像分割，由于效果出众而被广泛应用于各个行业[22]。U-Net模型将编码器中不同层级的特征跳跃连接到解码器中，实现了编码器和解码器的深度耦合。

由于U-Net是全卷积神经网络架构的一种，无法像CNN模型一样用全连接神经网络处理飞行高度、马赫数和迎角组成的飞行条件向量。因此考虑将飞行高度、马赫数和迎角与飞行器外形信息矩阵组合为一个四通道的矩阵作为整个神经网络的输入，该矩阵的第一个通道为飞行器外形信息矩阵，第二至第四个通道分别是飞行高度、马赫数和迎角，其结构如图6所示。

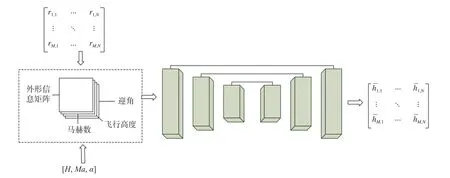
图6 U-Net结构Fig.6 Structure of U-Net

2 模拟结果与讨论

2.1 数据准备与预处理

在这项工作中，本文使用NNW-HyFLOW软件模拟得到了用于训练神经网络的气动热数据。由于没有涉及侧滑角，因此采用半模计算并将计算结果处理为全模的形式用于神经网络的训练。为了研究CNN、U-net两种模型在不同方面的性能，本文创建了以下3个不同的数据集。

数据集A：该数据集由9个不同锥角的钝锥在不同飞行条件下的物面热流数据组成。具体的飞行条件如表1所示。锥角为7°、8°、9°、10°、11°、12°、13°、14°、15°，飞行高度为20～60 km，马赫数为5～20，迎角为0°～20°。采用全因子设计法，每种外形可以得到252个不同的飞行状态，9种外形共有2268个算例。

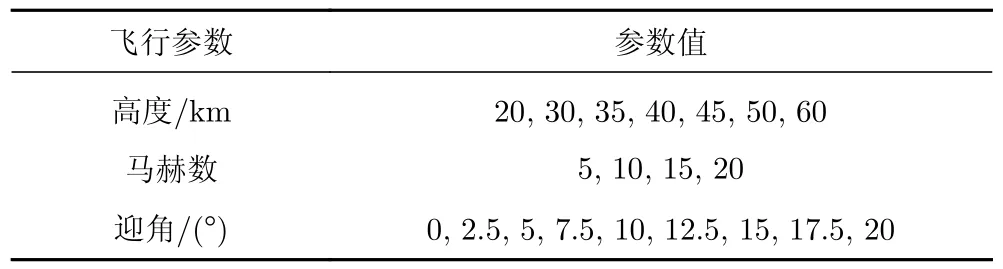
表1 飞行条件Table 1 Flight conditions

数据集B：为了考查模型在外形发生巨大变化时的热流预测能力，按照表1所示的飞行条件采用全因子设计法，针对锥角为7°的钝锥、双椭球、钝双锥和升力体4种外形进行CFD模拟。每种外形可得到252个样本，整个数据集共有1008个样本。

数据集C：数据集C是数据集A的子集，由锥角为7°的钝锥表面热流数据组成，用于研究不考虑飞行器外形变化时模型的热流预测能力。

本文的4种模型外形为：不同锥角的钝锥模型球头半径均为10 mm，锥身长为190 mm；钝双锥模型球头半径为10 mm，第一锥角为7°，第一锥身长为190 mm，第二锥角为12°，第二锥身长为100 mm；双椭球模型采用文献[23]中给出的数学模型并设置总长为200 mm；升力体外形是自主设计生成的，该外形球头半径为20 mm，后掠角为10°，总长为1350 mm，其具体外形如图7所示。

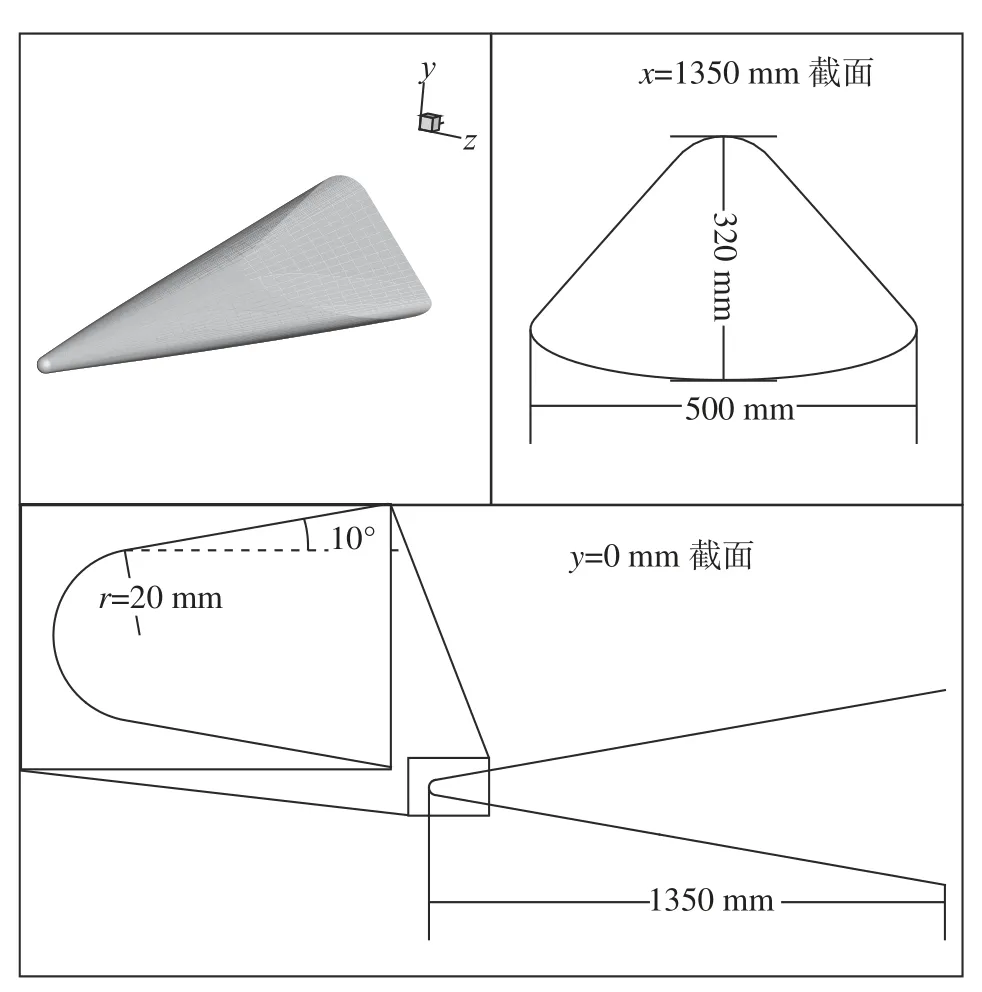
图7 升力体几何示意图Fig.7 Schematic diagram of the lifting body geometry

设置输入输出矩阵的尺寸为128 × 128，采用1.1节所述的几何表达方法对数据集中的所有样本进行数据预处理。针对CNN模型，在数据的边缘添加虚拟单元以降低模型对边缘区域的预测误差，虚拟单元的值从矩阵的内层映射得到，具体的设置方法如图8所示。考虑到添加了虚拟单元会影响模型的网络结构，为了保证添加虚拟单元前后不影响几何特征编码器的输出尺寸，设置添加6层虚拟单元，添加了虚拟单元后输出的尺寸变为140 × 140。

图8 虚拟单元添加方法Fig.8 Method of adding virtual cells

2.2 网络参数设置

根据输入输出的尺寸，分别对两种模型的具体网络结构进行设计，CNN模型3个组件的具体网络参数如表2～表4所示，U-Net模型的具体参数如表5所示。

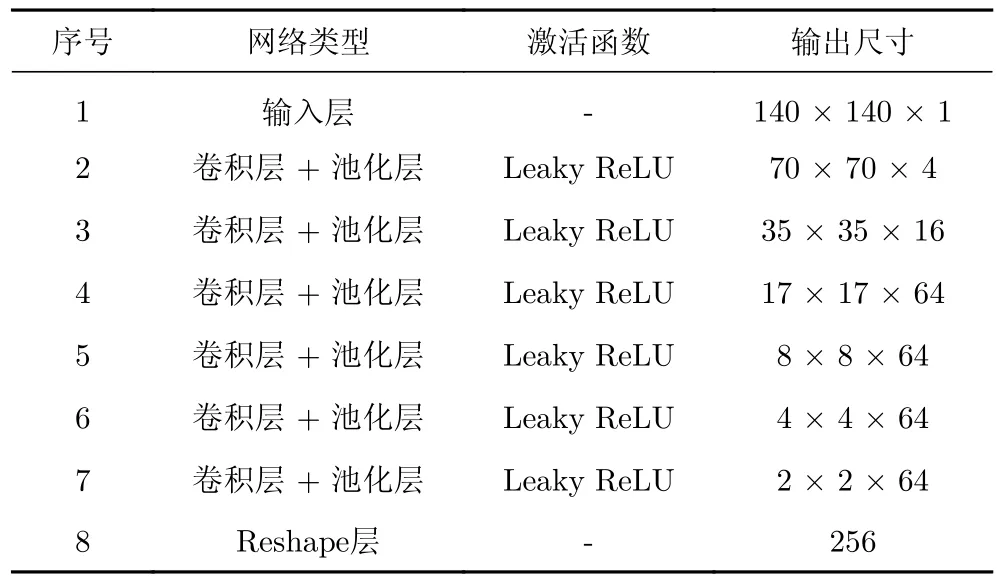
表2 几何信息编码器网络结构Table 2 Structure of the geometric information encoder

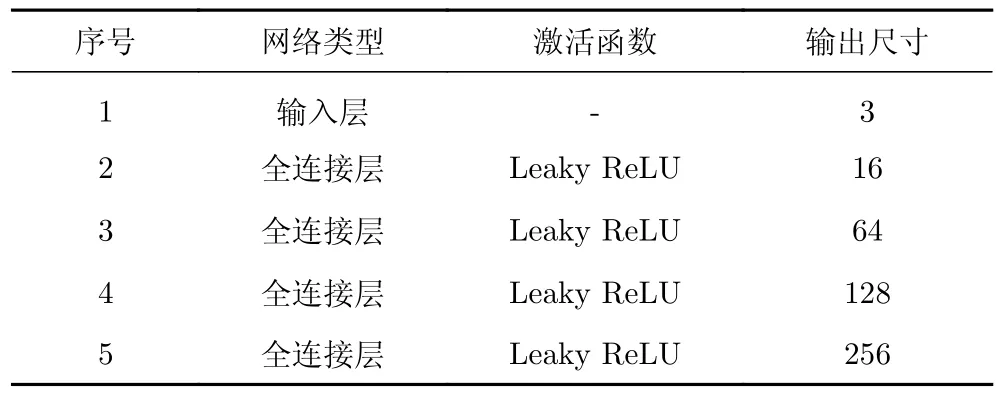
表3 飞行条件编码器网络结构Table 3 Structure of the flight condition encoder

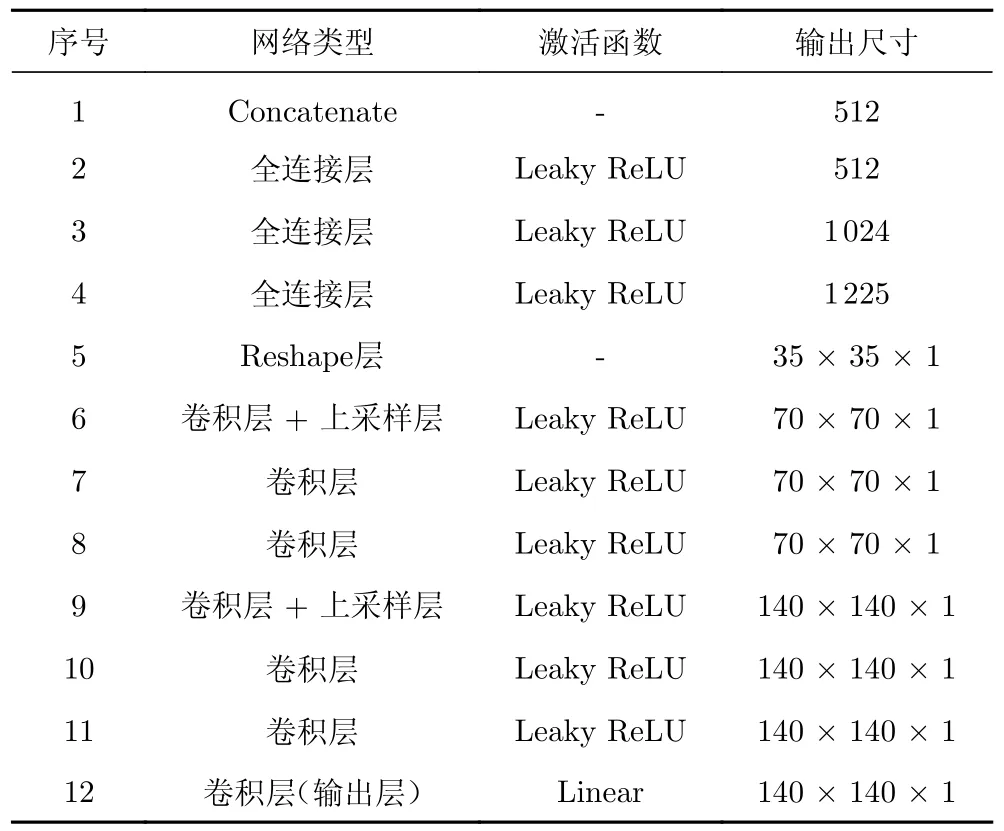
表4 热流解码器网络结构Table 4 Structure of the heat flux decoder

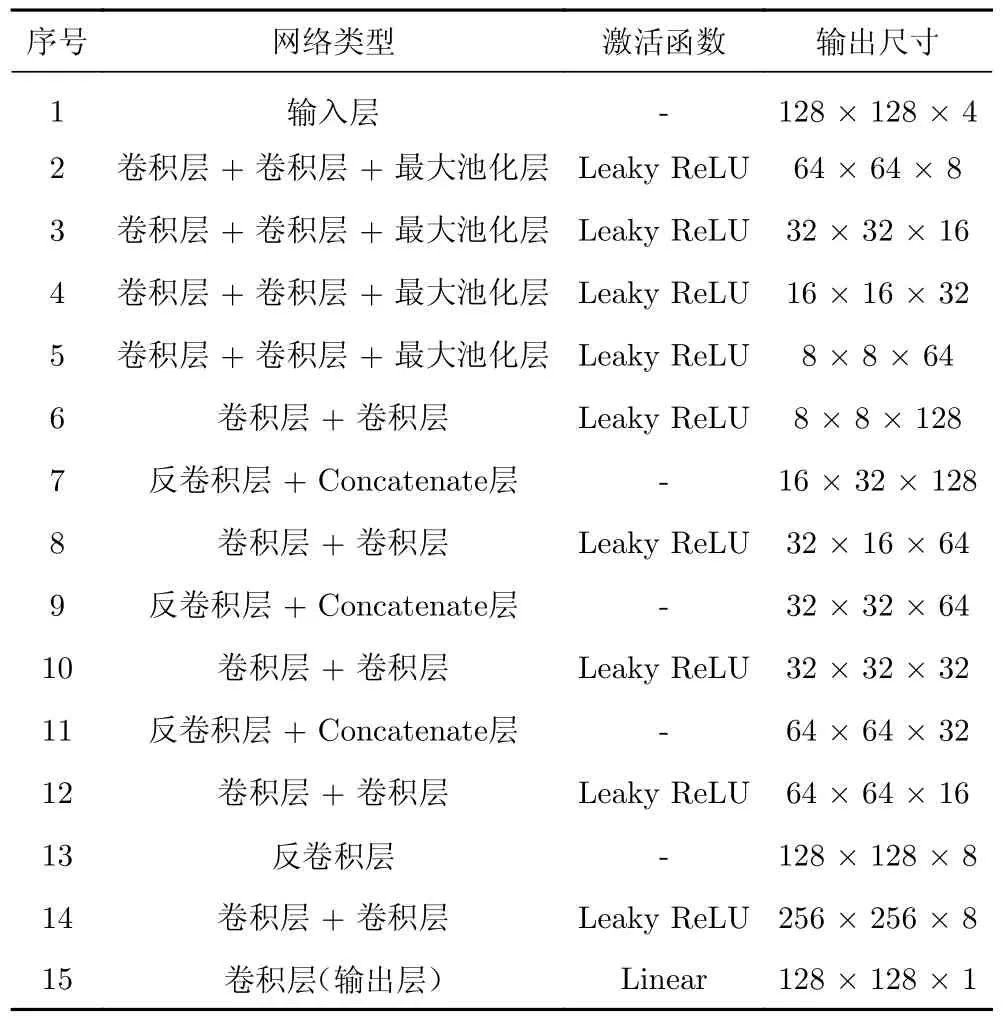
表5 U-Net网络结构Table 5 Structure of U-Net

由于CNN模型的训练数据是添加了虚拟单元的，而虚拟单元区域的误差是不需要考虑的，因此在损失函数和模型评估指标中仅统计其有效区域的误差。本文选用绝对百分比误差e（absolute percent error,APE）衡量单个样本的预测误差，用平均绝对百分比误差l（mean absolute percent error, MAPE）作为损失函数，二者可由式（4）～式（7）计算得到：

其中：hij和分别表示热流矩阵中 (i,j)位置处的CFD热流值和预测热流值，S表示当前数据集的样本个数。由于不同条件下的热流差别巨大，相对误差更能反映模型的真实预测精度，因此本文考虑采用MAPE作为模型性能的评价指标。为了全面考查模型对热流的预测能力，以MAPE为基础设计了全局误差、高热流区域误差和最大热流值误差。全局误差是指飞行器整个物面上热流的平均绝对百分比误差，高热流区域误差是指高热流区域热流值的平均绝对百分比误差，最大热流值误差是指热流最大值的平均绝对百分比误差。

2.3 钝锥热流预测

将数据集A以4∶1的比例分为训练集和测试集，采用适应性矩估计优化器（adaptive moment estimation optimizer, Adam），设置学习率为0.0005，设置模型每次优化的样本数为64，对两种模型分别进行训练。在5000次训练后，U-Net模型在训练集和测试集上的误差分别为1.46%和1.51%，CNN模型在训练集和测试集上的误差分别为2.66%和2.92%，可以看出U-Net模型的预测精度是明显高于CNN模型的。两种模型的学习曲线如图9所示，同样可以看出在5000次训练后U-Net的误差明显更低，而且U-Net模型的训练收敛速度也略快于CNN模型。

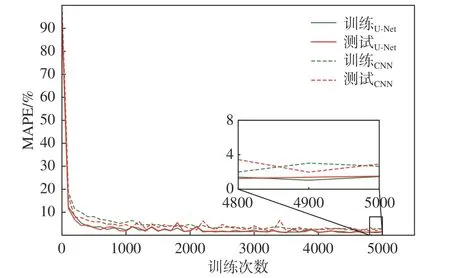
图9 CNN和U-Net在数据集A上的学习曲线Fig.9 Learning curves of CNN and U-Net trained by dataset A

对于数据集A，选择钝锥的球头区域作为高热流区域。测试集的3种误差结果见表6，结果表明，UNet不论是整体预测误差还是局部区域的预测误差均低于CNN模型。

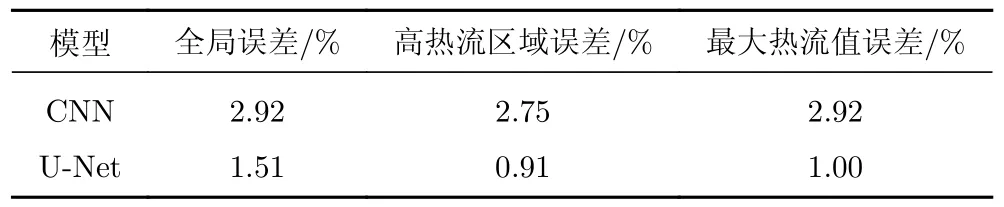
表6 CNN和U-Net模型在测试集上的预测误差Table 6 Prediction errors of CNN and U-Net on the test dataset

在测试集中随机抽取3个锥角不同的钝锥作为测试样本，3个样本的具体参数如表7所示，分别用两个模型对其热流分布进行预测，将不同位置（z= 0，y= 0，x= 50）的预测结果与CFD计算得到的热流值进行对比，其结果如图10所示。图中z= 0处热流变化曲线表示热流沿该线由下至上的变化，y= 0处热流变化曲线表示半模结果中热流沿该线由头部到身部的变化，x= 50处热流变化曲线表示半模结果中热流沿该线由下至上的变化。从图中可以看出，在大面积区域两种模型的预测结果与CFD模拟得到的结果均吻合良好，说明对不同锥角的钝锥组成的简单数据集，两种模型均有较高的预测精度，但在局部区域（x=50），U-Net模型的预测结果与CFD结果吻合得更好。

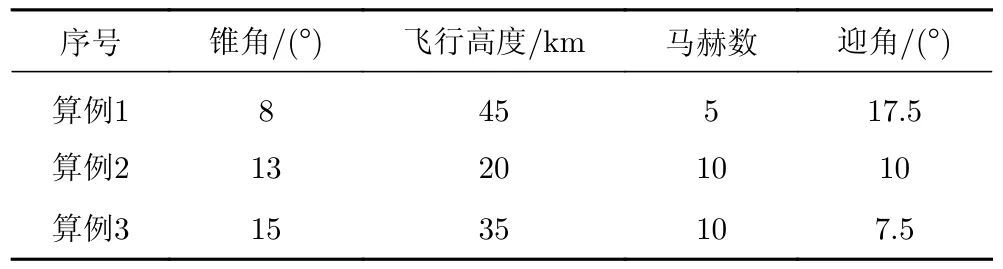
表7 钝锥测试算例参数Table 7 Parameters of the blunt cone test samples

图10 不同锥角钝锥局部位置热流对比（左：z = 0，中：y = 0，右：x = 50）Fig.10 Comparison of the heat flux in different areas of the blunt cones with different cone angles (left: z = 0, middle: y = 0, right: x = 50)

2.4 多类外形热流预测

两种模型在钝锥热流数据集上均有较好的预测效果，但钝锥的外形以及热流分布较简单，而且不同锥角的钝锥热流分布相似性高，因此无法体现模型对外形变化的感知能力。本小节考虑采用由钝锥、双椭球、钝双锥和升力体4种外形热流数据组成的数据集B对两种模型进行训练和测试。同样将数据集以4∶1的比例分为训练集和测试集，采用Adam优化器，设置学习率为0.0005，设置模型每次优化的样本数为64，对两种模型分别进行训练。在10000次训练后，CNN模型在训练集和测试集上的误差分别为4.78%和5.17%，U-Net模型在训练集和测试上的误差分别为1.63%和1.94%。在数据集变复杂之后，两种模型的预测误差有了明显增大，但U-Net模型仍然保持着精度上的优势。两种模型的学习曲线如图11所示，同样可以看出在10000次训练后U-Net模型具有更低的预测误差。

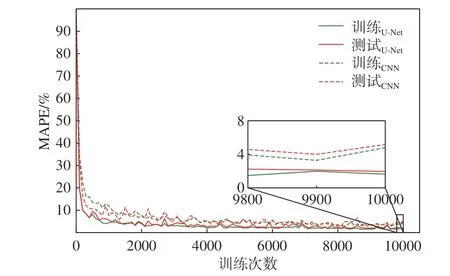
图11 CNN和U-Net在数据集B上的学习曲线Fig.11 Learning curves of CNN and U-Net trained by dataset B

从测试集中随机选取不同外形的样本各一个，用于对模型进行测试，4个样本的具体参数如表8所示。分别采用两种模型对4个样本进行预测，将不同位 置（z= 0，y= 0，x= 50、100、500）的 预测结果与CFD结果进行对比，其热流云图与局部位置的对比如图12～图15所示。从算例的对比可以看出，针对稍微简单的轴对称外形，钝锥和钝双锥两种模型在大面积区域与CFD结果吻合较好；针对一些变化较大的外形，例如升力体和双椭球，可以明显看到CNN模型预测的热流分布发生了较大的波动。尤其是在双椭球的第二椭球区域，CNN模型的预测结果出现了较大的偏差，而U-Net模型的预测结果则相对较好。这说明相比于CNN模型，U-Net模型对飞行器外形的感知能力更强，具有更高的预测精度。

表8 4类外形测试算例参数Table 8 Flight parameters for the different model geometries

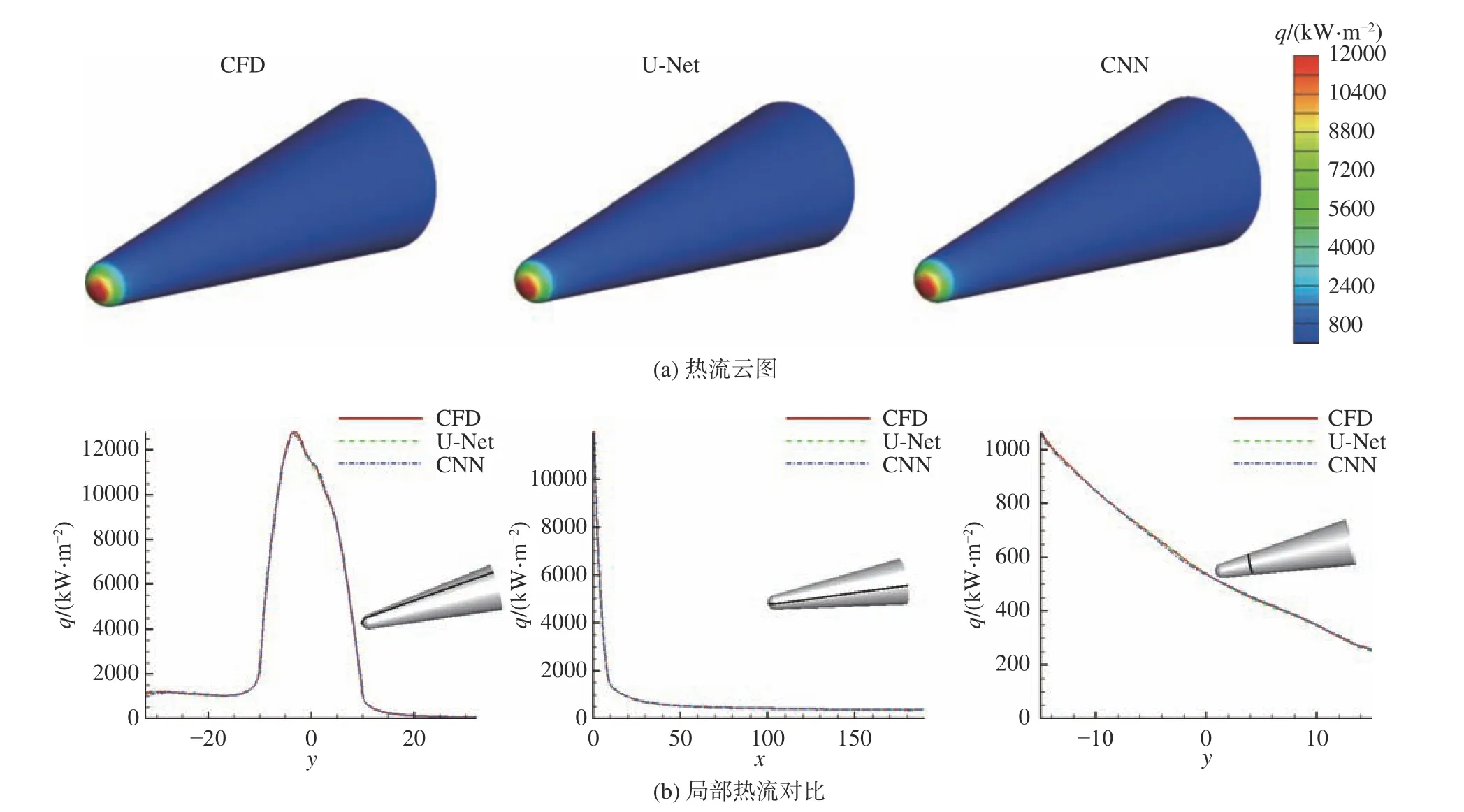
图12 钝锥的热流预测结果对比（左：z = 0，中：y = 0，右：x = 50）Fig.12 Comparison of the predicted heat flux of the blunt cone (left: z = 0, middle: y = 0, right: x = 50)

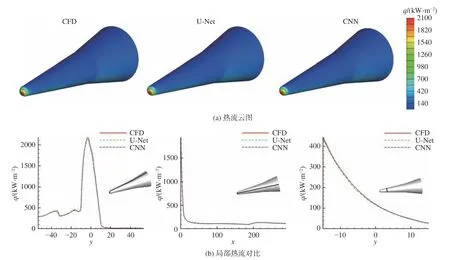
图13 钝双锥的热流预测结果对比（左：z = 0，中：y = 0，右：x = 50）Fig.13 Comparison of the predicted heat flux of the double cone (left: z = 0, middle: y = 0, right: x = 50)

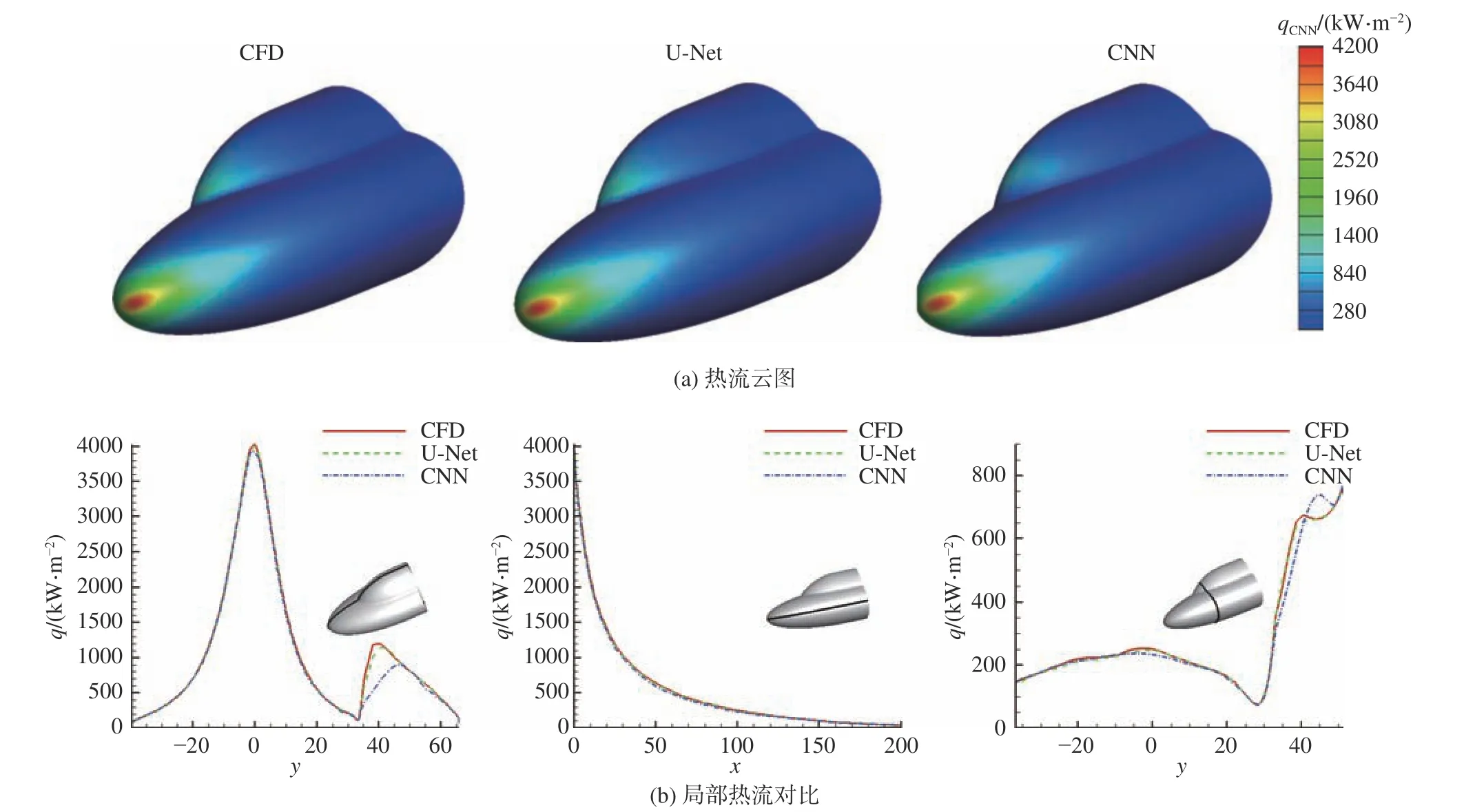
图15 双椭球的热流预测结果对比（左：z = 0，中：y = 0，右：x = 100）Fig.15 Comparison of the predicted heat flux of the double ellipsoid (left: z = 0, middle: y = 0, right: x = 100)

对双椭球的两个热流峰值的预测误差随训练次数的变化趋势进行考查，结果如图16所示。从图中可以看出两个模型对第一峰值的热流预测效果良好，其中U-Net模型的精度略高；但对第二个热流峰值的预测，CNN模型的预测结果明显存在较大的偏差，而U-Net模型也需要更多次的训练才能获得较好的预测效果。这是由于双椭球相比于其他外形会多一个热流峰值，该峰值是外形的变化造成的。图16的结果表明U-Net模型相比于CNN模型对外形变化的感知能力更强，因此其对热流的预测精度更高。另一方面，模型在第二峰值的误差在训练10000次时基本稳定，因此在数据集变复杂之后，模型需要增加训练次数才能获得良好的预测效果。

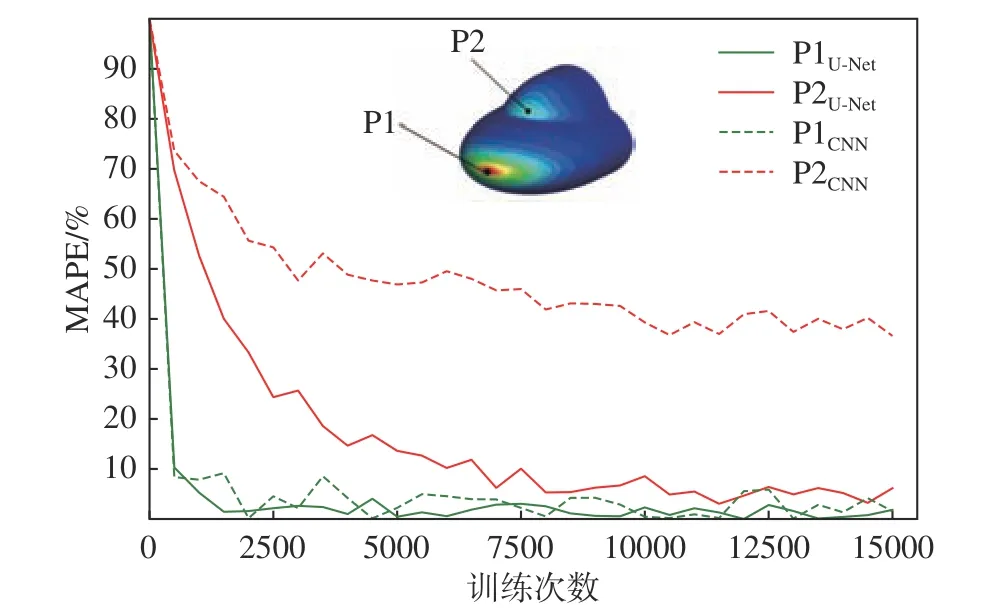
图16 两个热流峰值预测误差随训练次数的变化趋势Fig.16 Error variation of the two heat-flux peak values with the training times

2.5 与其他方法的对比

2.5.1 与RBF方法对比

RBF方法是由张智超[16]提出的一种基于径向基函数神经网络的气动热预测代理模型，对飞行器表面的每个点构建了正则化的径向基神经网络，并同时对这些网络进行训练。这是一种预测在不同飞行条件下的物面热流的方法，因为没有考虑飞行器的外形特征，所以该方法只能对单个外形的热流数据进行建模。

对于不考虑外形变化的气动热预测模型，更重要的是如何用更少的训练数据来提高模型预测精度。为了研究训练样本数量对模型的影响，从数据集C中选取不同数量的样本训练CNN模型、U-Net模型和RBF模型，将剩余的数据作为测试集，对比结果如图17所示。

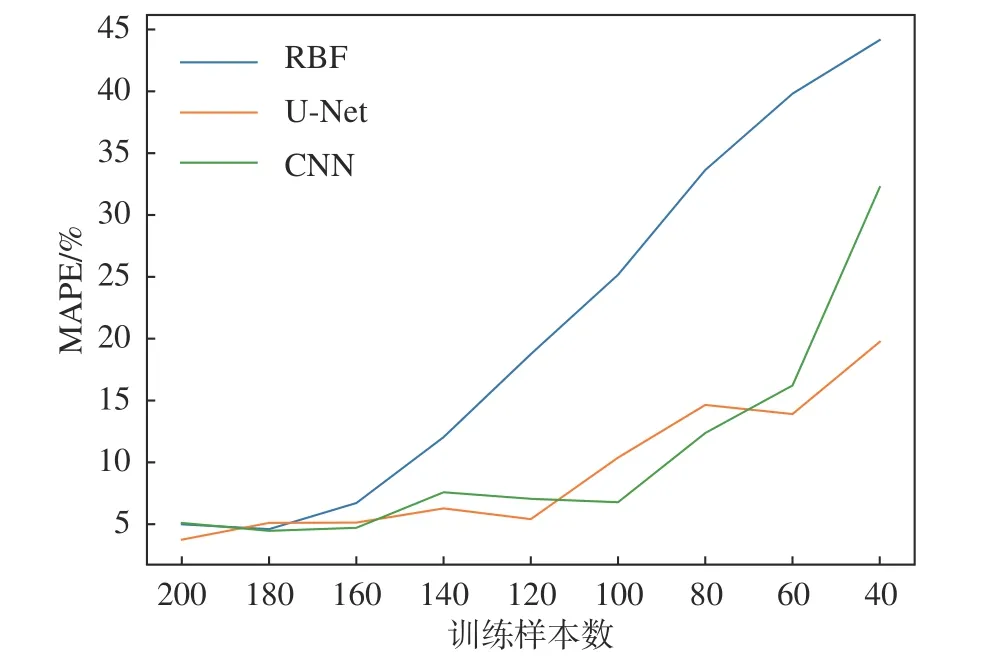
图17 不同训练样本数时三种模型的预测误差Fig.17 Prediction errors of the three models trained by datasets with different numbers of samples

对比结果表明，当样本量较大时，3种模型的预测精度相似，但随着样本量的减少，CNN模型和UNet模型的预测精度明显高于RBF模型，其中UNet模型在训练样本数量较少时预测误差最低。这表明本文所采用的U-Net模型在训练数据较少的情况下仍具有相对较强的学习能力。

2.5.2 与SA-HFNet对比

Li等[18]提出的SA-HFNet是一种基于深度学习的气动热预测方法。为了考查本文采用的两种模型的训练效率，本小节使用数据集A在配备Inter(R)Core(TM) i9-10940X CPU @ 3.30 GHz 3.31 GHz和NVIDIA GeForce RTX 3090的 计 算 机 上 对CNN、U-Net和SA-HFNet模型三个模型进行训练和测试。抛开精度谈效率是没有意义的，所以在模型训练时设置当测试集的平均绝对百分比误差达到2%时即停止训练。

训练结果的对比如表9所示，可以看出，CNN模型和U-Net模型能够用更少的训练时间获得与SAHFNet相当的精度。CNN与U-Net相比，虽然时间的消耗相差不大，但是U-Net的训练次数远小于CNN模型，这是因为U-Net模型收敛得更快。CNN模型和U-Net模型能够在短时间内达到目标精度的原因有二：一方面，权值共享是卷积神经网络最突出的特征之一，这使得其在训练中比全连接神经网络更高效；另一方面，与SA-HFNet不同，CNN模型和U-Net模型以整个表面的热流为单个样本，而SA-HFNet以单个点的热流为单个样本，这导致SA-HFNet的训练样本数量远大于CNN模型和U-Net模型。

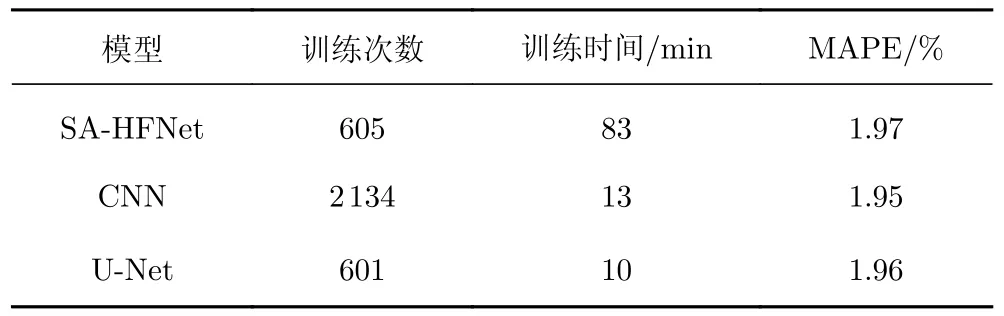
表9 SA-HFNet、CNN和U-Net训练效率对比Table 9 Comparison of the training efficiency of SA-HFNet,CNN and U-Net

3 结 论

本文针对气动热的快速预测问题，将卷积神经网络应用于高超声速飞行器的气动热预测，提出了一种三维曲面几何特征表达方法，并基于该方法通过两种不同架构的神经网络模型实现了不同外形飞行器在不同飞行条件下的表面热流预测。通过对多种典型外形的热流预测结果对比，以及与同类方法的对比，可以得到以下结论：

1） 基于编码器-解码器架构的CNN模型与UNet模型针对简单外形均有不错的预测精度。但当外形变复杂时，基于U-Net的气动热预测模型具有更强的外形感知能力，因此预测精度更高。另一方面针对更复杂的外形，模型需要更多的训练次数才能获得良好的预测效果。

2） 在不考虑飞行器的外形变化时，U-Net模型具有更强的学习能力，能够在训练数据较少的情况下获得相对较高的预测精度。

3） 由于采用了大量的卷积神经网络结构，本文所提方法训练效率较高，其中U-Net模型具有更快的收敛速度，能够在更短时间内达到目标精度。

本文针对提出的方法，使用了一些典型高超声速飞行器外形进行了仿真测试，下一步将针对更复杂、更贴近工程应用的飞行器外形进行研究。同时对方法的泛化性进行深入探讨，对气动热以外的其他气动特性进行建模预测。