多孔介质传热模型在多孔壁湍流中的适用性
赵泽灏,张金龙,董宇红,*
(1.上海大学 力学与工程科学学院,上海市应用数学和力学研究所,上海 200072;2.上海市能源工程力学重点实验室,上海飞行器力学与控制研究院,上海 200072)
0 引 言
多孔介质广泛存在于自然界和工业界,除了对动量输运的影响之外,多孔介质对传热的影响也是一个重要的问题。近年来,金属泡沫材料这类高孔隙率的多孔介质因为其金属本身出色的传热性能在设备热管理、能源储存等领域得到了广泛的关注。作为一种多孔材料,金属泡沫相比普通金属的特点在于比表面积巨大,且其内部不同的孔隙结构可展现出不同的物理特性。同时,金属泡沫材料因其高孔隙率和高导热系数等特点在热交换器应用方面具有特殊的优势[1-3]。
高孔隙率金属介质在设计优化过程中,预测其传热性能的关键在于多孔介质传热模型的准确性。局部热平衡(local thermal equilibrium, LTE)模型假设多孔介质内某点固体相与当地流体相温度相同,只用一个控制方程描述温度场;局部非热平衡(local thermal non-equilibrium, LTNE)模型则假设多孔介质内一点固体相与当地流体相的温度可以不同,需要针对流固两相采用两个不同的控制方程来描述多孔介质温度场。由于LTE模型简化程度高、方便求解,且计算时间短、计算成本低,是多孔介质传热问题数值求解中运用最为广泛的模型之一。事实上,只有当多孔介质内流体和固体两相间的导热足够快速,以至于相间的局部温差可以忽略不计时,LTE模型才能普遍成立。然而,工程中也存在多孔介质相间温差过大的情况。比如扩散传热和对流传热之间存在显著差异,或固体多孔基质中的颗粒尺寸与热边界层厚度相当,或基质颗粒超过热边界层厚度[4],这时局部热平衡假设的局限性就会凸显。
关于LTE模型适用范围的研究,Whitaker等[5-6]率先用孔隙率、密度、比热容、流体相和固体相的导热系数建立了LTE的适用准则,但没有考虑流固两相间传热的影响。Kim和Jang[7]考虑了相间传热的影响,用普朗特数、雷诺数和达西数等无量纲数建立了新的适用准则。之后,Zhang和 Liu[8]在恒定热通量边界条件下研究了充满球体的多孔槽道内的强迫对流问题。他们认为在流体导热系数不变的情况下,固体相导热系数越小,LTE模型的有效性越高,并据此提出了一个新的适用准则。
Kuznetsov[9]使用摄动法对二维多孔介质槽道流进行了分析,发现LTE模型在低达西数时边界处更加有效,而在高达西数时远离边界的流场则未必有效。Lee和Vafai[10]给出了Kuznetsov[9]所研究的模型的精确解,考查了不同Biot数下LTE模型的有效性,并给出了一个经验准则。
Vafai和Sözen[11]使用数值方法研究了充满多孔介质的水平槽道内的强迫对流,认为LTE模型对于雷诺数和达西数非常敏感,两个参数中只要有一个偏大时LTE模型就不再有效,且发现LTE模型在固体相的导热系数较低时表现更好。Amiri和Vafai[12]通过计算全域内流固两相的最大绝对温差,研究了瞬态过程中LTE模型的表现,发现在低达西数且流体相和固体相的导热系数之比接近1时,LTE模型适用性较好,于是认为流体相和固体相导热系数之比是评估LTE模型是否有效的关键参数。Singh等[13]研究比较了LTE模型与LTNE模型在不同雷诺数下(Re=10~10000)的表现。他们的研究表明,当流体和多孔介质分别为水和玻璃球时,由于两相间的高导热性,雷诺数越大,LTE模型与LTNE模型的预测结果越接近;而当流体和多孔介质分别为空气和金属线材时,由于金属的高导热性,上述两个模型所得结果的差别显著。Singh等[14]又以水为流体介质对振荡的温度边界下填满钢质球型颗粒的圆管实验结果进行比较,发现LTNE模型与实验结果非常接近,而LTE模型失真严重。并且,LTNE模型对温度变化的响应也与实验结果很吻合,而LTE模型与实验结果完全不吻合。
上述研究多是以低孔隙率、球形颗粒的传统多孔介质为前提进行的,对于以金属泡沫为代表的新型高孔隙率多孔介质研究较少。Pulvirenti等[15]数值研究了金属泡沫内部传热的性质,依据金属的极高导热系数这一特点提出理想金属泡沫(ideal metal foams,IMF)假设,结合边界条件将两方程的LTNE模型简化为单方程模型,减少了计算量,但他们没有给出IMF模型的适用准则。Freitas等[16]分析了充满金属泡沫的矩形槽内混合对流热场的稳定性,采用了IMF模型,但也没有对IMF模型的适用性进行分析。随着以金属泡沫为代表的高孔隙率多孔介质得到越来越多的应用,研究并评估各类传热模型在金属泡沫传热问题中的适用性是非常必要的。
基于上述背景,本文以带有高孔隙率多孔介质壁面的槽道流为研究对象,采用直接数值模拟方法对多孔介质层内外的剪切湍流的流场和温度场进行模拟。在多孔介质层外流体区域通过有限差分方法求解不可压缩 Navier-Stokes 方程和温度对流扩散方程,在多孔介质层内使用修正的Darcy-Brinkman-Forchheimer模型描述多孔介质阻力。在验证计算结果的基础上,对LTE、LTNE和IMF三种多孔介质传热模型在不同参数下的有效性展开研究,并分析对比各多孔介质传热模型预测结果的差异,为高孔隙率多孔介质在湍流作用下的传热数值研究提供参考。需要指出的是,虽然雷诺数对模型的选择存在一定影响,但本文把不同Biot数及水和空气两类流体介质下多孔介质传热模型的有效性作为主要研究内容。
1 数理模型与计算方法
1.1 物理模型与控制方程
槽道湍流是典型的工程湍流的规范模型,对其动力学和热力学的研究可以推广到其他壁面剪切湍流。本文所采用的物理模型如图1所示,底部是多孔介质层,顶部是自由面。槽道的长、宽、高分别为Lx×Ly×Lz=2πh×1.2h×πh,其中流体层的高度为h,多孔介质层的厚度hp=0.2h。

图1 带有多孔介质层的槽道流和传热模型示意图Fig.1 Channel flow and heat transfer with porous layer
以h为特征长度,以壁面摩擦速度uτ为特征速度,以上下壁面的温度差为特征温度进行无量纲化,无量纲的控制方程如下:
多孔介质外流体区域:
其中,流向x、法向y和展向z的速度用u、v、w或ui(i= 1,2,3)表示,θ表示温度, δi1是Kronecker符号,代表了流向的驱动压力梯度,壁面摩擦雷诺数Reτ=ρfuτh/µ , 普朗特数Pr=µcf/kf, ρf是流体介质的密度,uτ是壁面摩擦速度, µ是流体介质的黏性系数,cf是流体介质的比热容,kf是流体介质的导热系数。
多孔介质区域:
式 中, 〈ui〉 是 多 孔 介 质 区 域 内 的 达 西 速 度, φ是 孔隙率,Di是多孔介质阻力,这里考虑高孔隙率故采用适用于较高流速的Darcy-Brinkman-Forchheimer模型[17]:
其中,Da=K/h2是达西数,K是多孔介质的渗透率,CF是Forchheimer数。在此我们使用Ergun[18]提出的模型其中dc是多孔介质单元的尺度。模型中的常数则采用Biasetto等[19]提出的适用于高孔隙率多孔介质的参数:A= 3.63,B=357.1。
流向和展向取周期性边界,上下壁面的边界条件为:
式中, θf和 θs为多孔介质区域流体相和固体相的温度。
本文在计算时使用速度、温度连续条件耦合多孔介质内流体和多孔介质层以上流体区域,考虑多孔介质固相基架在界面处主要与介质内流体进行直接热传递,设为绝热条件:
1.2 多孔介质传热模型
LTNE模型同时考虑固体相的温度 θ∗s和流体相的温度 θf∗以及两相之间的传热,是最接近真实传热状态的传热模型,具体控制方程为(本小节中上标 * 表示有量纲的量):
式中, ρ∗sc∗s是多孔介质固体相的密度乘比热容,即为固体相的单位体积热容量,同理 ρ∗fc∗f是多孔介质流体相的单位体积热容量,ks∗和kf∗分别为固体相和流体相的导热系数,h∗v是容积换热系数,表征了多孔介质内部流固两相的换热能力。
LTE模型假设多孔介质内部某点固体相和当地流体相具有相同温度,即 θ∗s=θf∗=θ∗,控制方程为:
IMF模型在LTNE模型的基础上,假设多孔介质材料是泡沫金属,考虑金属出色的传热能力,导热系数远大于流体相的导热系数,即k∗s≫kf∗,认为 ∇2θ∗s=0。结合本文算例,认为多孔介质内部固体相的温度总是与底部的温度相同,即 θs∗=θ∗bottom,控制方程为:
将式(10~13)无量纲化,可以得到3种模型无量纲形式的传热方程:
LTNE模型:
LTE模型:
IMF模型:
式中, ρsfcsf=(ρ∗sc∗s)/(ρ∗fc∗f)是固体相和流体相的单位体积热容量之比,ksf=ks∗/kf∗是固体相和流体相的导热系数之比, ρsfceff=(1-φ)(ρsfcsf)+φ是无量纲的等效单位体积热容,keff=(1-φ)ksf+φ是无量纲的等效导热系数,Bi=h∗vh2/kf∗是Biot数,表征了流固两相间的传热能力。
LTNE模型所用的假设最少,是3种模型中适用范围最广的模型。从实验研究中[13-14]也可以看到LTNE模型准确预测了与金属相关的多孔介质传热问题;另外,从方程上看,可以认为LTE模型和IMF模型分别是在LTNE模型的基础上增加了不同的假设简化得到的。然而,LTNE模型的不足在于方程求解复杂,计算量大。综上所述,可以使用LTNE模型的结果作为比较基准,验证LTE模型和IMF模型的有效性。
1.3 计算方法和程序验证
在对带有高孔隙率多孔介质壁面槽道湍流及其传热进行的直接数值模拟中,所有控制方程均是在交错网格上进行空间离散,为保证分辨率,在上部自由面和多孔介质界面附近均采用了法向加密网格处理。空间上均采用二阶中心差分进行离散化,时间上使用混合三步Runge-Kutta 格式结合Crank-Nicholson格式进行离散[20]。压力泊松方程的求解被用来保证散度为零的质量守恒条件。计算域流向、法向和展向网格为Nx×Ny×Nz=128×192×128,其中多孔介质层内的法向网格数为32。
关于计算方法和程序的验证,本研究组已经从带有多孔介质的剪切壁湍流模型和多参数算例进行了可靠的验证考查工作,具体详见前期的工作[21-25]。这些相关数值结果以及与其他实验和典型算例的比较提供了我们数值方法的细节,能够保证本文计算方法、程序和数值结果的可靠性。
高通滤波器的设计步骤很简单,如图1所示[4]。对于归一低通滤波器的设计采用插入损耗法(insertion loss method),该方法采用网络综合技术设计出有完整的特定频率响应的滤波器。
2 结果与讨论
由于铝的低密度、廉价等特点,泡沫铝是金属泡沫领域最具潜力的材料,本文的多孔介质参数参考了泡沫铝的各项数据。在流体方面,则选择了空气和水这两个最常见的流体作为工作介质。固体相和流体相的材料参数如表1所示。

表1 流体和固体介质的热力学参数Table 1 Thermodynamic parameters of fluid and solid media
本文算例:Reτ= 180, φ = 0.9,Da=1×10-5。由于Bi与介质的热力学参数、多孔介质结构、流速等因素相关,综合本文所考虑多孔金属介质的特性参数范围以及前人的工作[26-27],选取Bi= 300~30000。各算例参数选择如表2所示。

表2 不同算例的热力学参数Table 2 Thermodynamic parameters of different cases
本文的统计数据取自流场以及温度场充分发展之后足够长的时间段。为了比较不同传热模型所预测热场的差异,对该段时间内的流场以及温度场取法向平面平均和时间平均,得到了流场的平均温度分布以及温度脉动均方根 θ′rms分布[28]。另外,为了表达方便,将多孔介质区域流体相的平均温度和温度脉动均方根也记为 θ¯ 和 θr′ms。
2.1 “空气-泡沫铝”多孔介质壁湍流的传热问题
图2比较了“空气-泡沫铝”传热问题在3种传热模型下的平均温度。不同的Bi下,IMF模型与LTNE模型得到的结果基本一致,而LTE模型与LTNE模型的结果有很大偏差,并且随着Bi的增加,偏差不断增加。另外,从LTNE模型所计算出来的固体相的温度分布可以看到,在“空气-泡沫铝”中固体相的温度分布呈一直线,与IMF假设中的∇2θs=0相符,并且数值上固体相的温度也与底面温度基本一致,与我们所预估的 θs=1相符合。
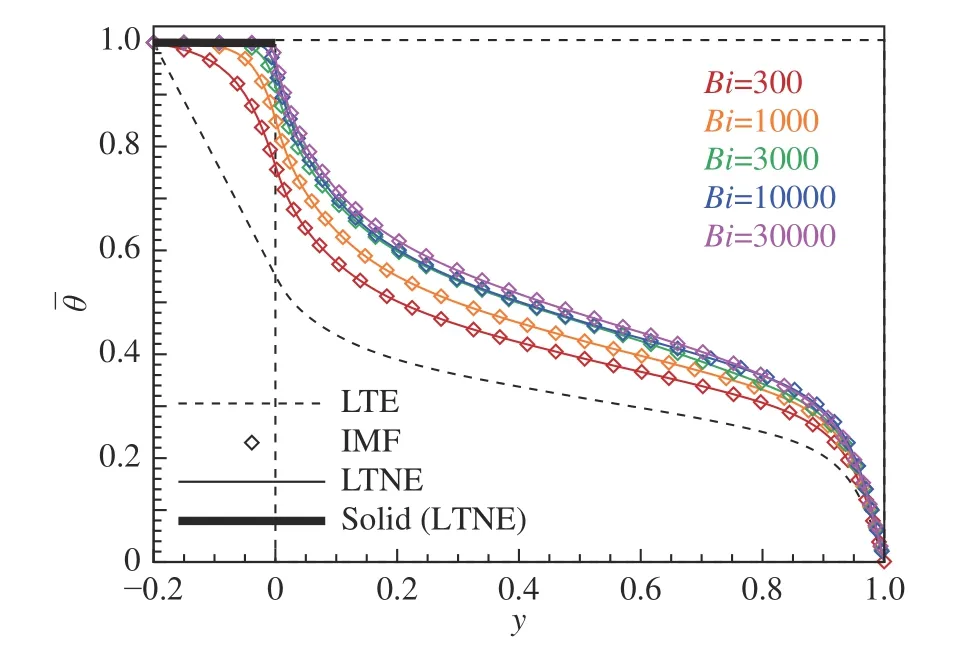
图2 “空气-泡沫铝”由3种传热模型所得平均温度沿法向的剖面图Fig.2 Average temperature profiles from three heat transfer models in "Air-Al foam"
图3比较了“空气-泡沫铝” 传热问题在3种传热模型下的温度脉动均方根。不同的Bi下,IMF模型得到的结果与LTNE模型得到的结果仍然基本一致。Bi=300时,多孔介质层内除交界面附近区域(y<-0.05),LTE模型的结果与LTNE模型吻合较好,但LTE模型在交界面附近区域以及多孔介质外流体区域低估了温度脉动均方根。LTNE模型所预测的温度脉动均方根随着Bi的增加不断增加,而LTE模型的等效单位体积热容和等效导热系数都没有考虑Bi的影响,因此与LTNE模型的结果比较,LTE模型对于温度脉动均方根的低估随着Bi不断增加。
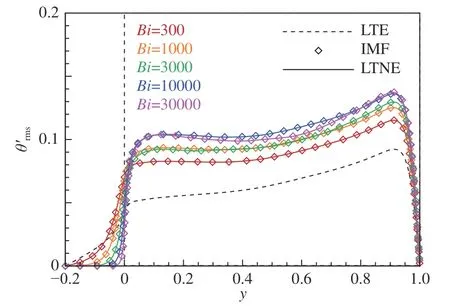
图3 “空气-泡沫铝”由3种传热模型所得温度脉动均方根沿法向的剖面图Fig.3 Temperature fluctuation intensities from three heat transfer models in "Air-Al foam"
结合图2和图3可以看出,在“空气-泡沫铝”的传热问题中IMF模型在不同的Bi下都能和LTNE模型的结果吻合得很好,因此在计算“空气-泡沫铝”的多孔介质传热问题时,相比两个控制方程的LTNE模型,只需要一个控制方程、计算量更小的IMF模型是一个很好的替代。
图4比较了LTE模型和不同Bi下LTNE模型计算所得流体相的平均温度和温度脉动均方根。图4(a)中,槽道总体平均温度随着Bi的增大而增大,这是因为随着Bi的增大,固体相和流体相之间的传热能力增强,更多的热量由固体相传至流体相。在多孔介质外流体区域和交界面附近区域,温度脉动均方根随着Bi的增大而增大;多孔介质层内除交界面附近区域外的温度脉动均方根则随着Bi的增加而减小,这是因为在大Bi时,多孔介质内流体温度的法向梯度较小,且由对流导致的温度变化可以通过固体相与流体相之间的传热快速补偿。
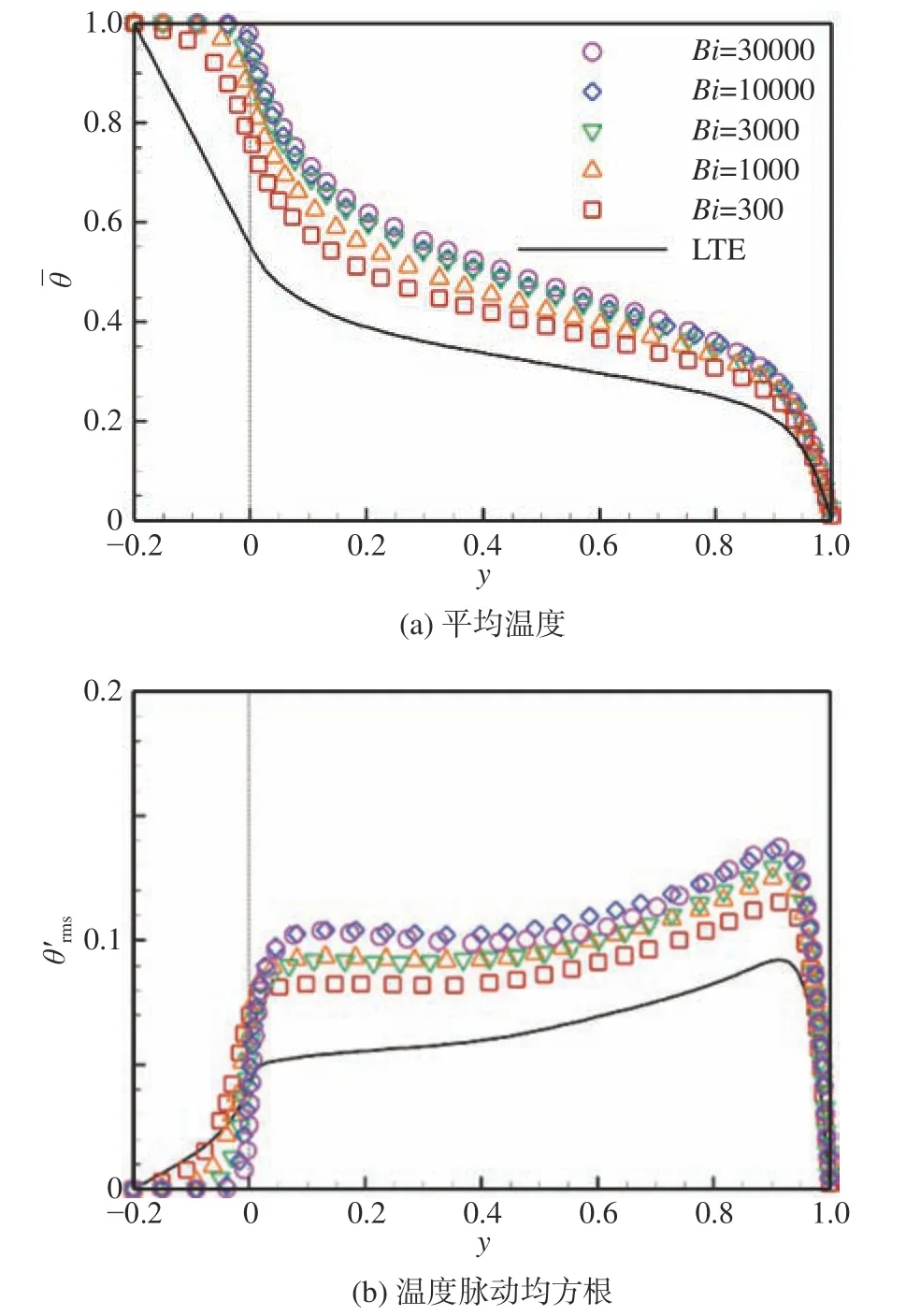
图4 “空气-泡沫铝”在不同Bi下流体相的平均温度和温度脉动均方根Fig.4 Average temperature profiles and temperature fluctuation intensities in "Air-Al foam" at different Bi
2.2 “水-泡沫铝” 多孔介质壁湍流的传热问题
图5比较了“水-泡沫铝”传热问题在三种传热模型下的平均温度。Bi=300时,与其他Bi的结果比较,三个模型的平均温度相对接近,但是LTNE模型中的固体相温度与流体温度存在明显差异。随着Bi的增加,LTE模型和IMF模型与LTNE模型结果的偏差越来越大,其中,IMF模型与LTNE模型的偏差相对较小。LTE模型的平均温度低于LTNE模型的平均温度;而IMF模型的平均温度高于LTNE模型的平均温度。这是因为在IMF算例中固体相的温度恒定为底壁的温度,与用LTNE计算出来的固体相温度相比,高估了固体相的温度。

图5 “水-泡沫铝”由三种传热模型所得平均温度沿法向的剖面图Fig.5 Average temperature profiles from three heat transfer models in "Water-Al foam"
图6给出了不同Bi下“水-泡沫铝”传热问题在不同传热模型中温度脉动均方根的对比。Bi=300时,IMF模型的结果与LTNE模型的结果基本一致;在交界面附近,相比LTNE模型,LTE模型明显低估了温度脉动均方根,而在自由面附近,LTE模型的结果与LTNE模型的结果接近。随着Bi的增加,在多孔介质外流体区域,将IMF模型与LTNE模型的温度脉动均方根对比,显示出高估的变化趋势;而LTE模型则明显低估了多孔介质外流体区域的温度脉动均方根。

图6 “水-泡沫铝”由三种传热模型所得温度脉动均方根沿法向的剖面图Fig.6 Temperature fluctuation intensities from three heat transfer models in "Water-Al foam"
值得注意的一点是,在多孔介质层内除交界面附近区域,LTE模型与LTNE模型的温度脉动均方根的偏差随Bi的增加不断减小,而IMF模型与LTNE模型的温度脉动均方根的偏差不断增大。这是因为IMF模型中所预估的固体相温度恒等于底壁温度。在“水-泡沫铝”中IMF模型高估了固体相的温度,并且随着Bi的增加,固体相向流体相的传热增加,固体相温度降低,IMF模型对固体相温度的高估也相应变大。同时,因为Bi的增加,在IMF模型中流体相温度的法向梯度变小,且由对流导致的温度变化可以通过固体相与流体相之间的传热快速补偿,因此低估了对流带来的温度脉动。
图7比较了LTE模型和不同Bi下LTNE模型得到的流体相的平均温度和温度脉动均方根。图7(a)中,随着Bi的增加,流体相从固体相得到了更多的热量,平均温度增加。在交界面处温度脉动均方根的峰值接近;而在多孔介质外流体区域,Bi越大,温度脉动越大,在多孔介质层则有相反的趋势。

图7 “水-泡沫铝”在不同Bi下流体相的平均温度和温度脉动均方根Fig.7 Average temperature profiles and temperature fluctuation intensities in "Water-Al foam" at different Bi
综合考虑“空气-泡沫铝”和“水-泡沫铝”传热问题的结果:在“空气-泡沫铝”中,Bi改变对IMF模型和LTNE模型结果一致性的影响很小;而在“水-泡沫铝”中,IMF模型和LTNE模型结果的差异性随着Bi的增大而增大。这是因为空气的比热容很小,导致只需要很小的热量就能改变空气的温度,且由于多孔介质内部流速低,对流传热对热量传递的贡献小,此外空气的Pr小,传热能力弱,不能及时将热量传递出去,最终导致固体相的温度与底壁温度的差距很小;而水的比热容很大,相应改变水的温度需要极多的热量,且由于水的Pr大,相比空气能更快地将热量传递到低温区域,Bi增大时,固体相向流体传递了大量的热却无法及时通过固体相内部的热传导得到补充,因此在“水-泡沫铝”算例中,离底壁越远,固体相的温度越低。
图8给出了LTNE模型计算得到的多孔介质层内固体相和流体相平均温度之差。可以看到,在“空气-泡沫铝”和“水-泡沫铝”中存在相同趋势:Bi越大,两相的温度差越小。在Bi= 30000的算例中,除了交界面附近,流固两相的温差几乎可以忽略不计。这说明LTE所假定的 θs=θf在远离交界面的多孔介质区域是适用的,且两相之间的传热能力越强,Bi越大,LTE的适用性越强,这与前人的研究[8,10]一致。但是从图2和图5所显示的结果来看,LTE与LTNE之间的偏差却随着Bi的增大而增大,这是因为LTE模型所预估的等效单位体积热容量 ρeffceff以及等效导热系数keff只考虑了孔隙率的影响[29-32],没有考虑流固两相之间的传热,即Bi的影响,低估了多孔介质层内的传热能力。

图8 LTNE模型所得的多孔介质层内固体相与流体相的温度差Fig.8 Temperature difference between solid and fluid phases in the porous layer calculated by the LTNE model
图2中固体相温度的分布以及IMF模型与LTNE模型结果的一致性表明IMF在“空气-泡沫铝”传热问题中是非常有效的。但是图5中IMF模型与LTNE模型结果的差异性表明IMF模型在“水-泡沫铝”这类大比热容、大Pr的流体介质中表现不佳。然而,进一步观察图5中不同Bi下的固体相温度可以发现,虽然离底壁越远,固体相与底壁的温差越大,但固体相的温度分布依然满足IMF模型中所作的假设 ∇2θs=0,表明IMF模型在一定程度上依然可以适用于大比热容、大Pr的流体介质,条件是在预估固体相温度分布的时候需要将比热容、流固两相间的传热能力纳入考量。
2.3 Nusselt数和Biot数的进一步讨论
为了进一步分析比较不同模型对槽道传热能力的预估,本文计算了不同算例中三种模型所得热场的Nusselt数(Nu):
图9给出了LTE和IMF模型计算所得的Nu与LTNE模型计算所得的Nu之比和Bi的关系。可以看到,IMF模型会高估槽道的传热能力,而传统的LTE模型则会低估槽道的传热能力,并且随着Bi的增加,LTE模型和IMF模型结果与LTNE模型结果的偏差越来越大。在本文所考虑的参数范围内,相较于LTE模型,IMF模型与LTNE模型结果的偏差更小。

图9 LTE和IMF模型计算的Nu与LTNE模型计算的Nu之比和Bi的关系Fig.9 Ratios of Nu calculated from LTE and IMF models to Nu calculated from LTNE model as a function of Bi
图10给出了LTNE模型计算所得的Nu和Bi的关系。可以看到,不论是“空气-泡沫铝”算例还是“水-泡沫铝”算例,槽道的Nu随着Bi增加不断提高。在本文所选取的参数范围内,Nu与Bi存在标度律关系Nu~Bi0.05。
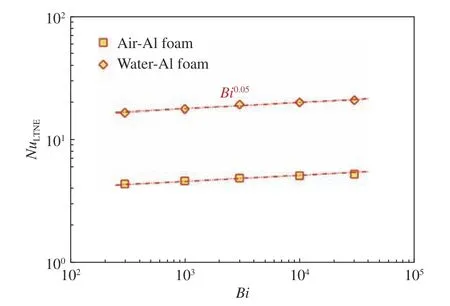
图10 LTNE模型计算所得的Nu与Bi的关系Fig.10 Nu calculated by the LTNE model as a function of Bi
3 结 论
本文以“空气-泡沫铝”和“水-泡沫铝”为例,运用直接数值模拟研究了高孔隙率多孔介质不同传热模型在不同Bi下的适用性。由于LTNE模型考虑多孔介质的传热时,无相关的简化和假设,在本文所考虑的参数范围内该模型可准确描述不同介质的传热问题,因此本文着重研究了不同Bi下LTE模型和IMF模型的适用性,得到以下主要结论:
1)对于空气这类小比热容、小Pr的流体介质,IMF模型在不同Bi下都有很强的适用性,可以代替LTNE计算金属泡沫的多孔介质传热问题。
2)对于水这类大比热容、大Pr的流体介质,IMF模型的适用性随Bi的增大而降低,需要进一步结合流体介质的比热容、Pr和流固两相之间的传热能力等因素对固体相的温度分布进行预估。
3)LTE模型对于高孔隙率金属泡沫传热问题的适用性很差,会低估平均温度和温度脉动均方根。原因是LTE模型中估计的等效单位体积热容量ρeffceff以及等效导热系数keff只考虑了两相单位体积热容量、导热系数和孔隙率的影响,没有考虑流固两相间传热能力的影响,低估了多孔介质内部的传热能力。
在实际的换热器中,有时会使用热力学性质更好的流体介质来增加传热效率,因此对于这些流体介质在各种简化模型下的表现需要进一步研究。

