各向异性Kelvin泡沫胞元高径比对其流动传热特性的影响

张 超，孔祥壮，杜雁霞，王 娴，肖光明，*

(1.西安交通大学 航天航空学院，机械结构强度与振动国家重点实验室，陕西省先进飞行器服役环境与控制重点实验室，西安 710049；2.空天飞行空气动力科学技术全国重点实验室，绵阳 621000)

0 引 言

泡沫材料具有比表面积大、质量轻、高导热系数等[1]优点，被广泛应用于高超声速飞行器热管理系统中[2]，如用于高超声速飞行器前缘主动冷却结构的SiC泡沫[3]以及金属泡沫[4]。然而，真实泡沫材料的微细结构极度复杂无序，且具有明显的各向异性[5-6]，使得对泡沫材料内部流动传热特性的精确预测有较大困难。对于泡沫材料的微细结构表征，X射线断层成像技术是较为精确的方法[7-9]。该方法能完全还原泡沫骨架微细结构及孔隙分布特征，有非常高的精度。然而，受限于加工过程中一些结构参数的不可控，如前文提到的孔隙结构，使X射线断层成像技术无法高效地运用到结构优化设计的相关研究中。因此，为了进一步优化泡沫材料的传热性能，需要对真实泡沫材料微细结构进行关键特征提取，建立等效模型并对关键结构参数进行定量分析。

最初，许多学者不考虑泡沫材料的结构各向异性，采用各向同性的代表性单元表征泡沫材料微细结构。应用最为广泛的是Kelvin泡沫[10]，该结构提取了泡沫材料中的韧带、节点和孔3个关键参数，在泡沫材料的等效导热系数理论预测问题上具有较高精度，最早由Boomsma和Poulikakos[11]将其运用到泡沫材料等效导热系数的理论预测中，经过Dai等[12]对热流传递方向的修正，形成一套完整的理论体系。在此基础上，Yao等[13]通过改变节点形状及分布进一步优化了该模型，并采用实验进行验证，最大相对误差小于10%。上述研究中，泡沫结构各向异性对传热的影响被忽略；然而，自从Ranut等[14]通过ANSYS CFX计算真实泡沫结构沿3个正交方向的对流导热系数和压降，发现3个正交方向的导热系数和压降均存在较大差异，泡沫材料结构各向异性对传热各向异性的影响逐渐被一些学者关注。

泡沫结构各向异性产生的主要原因是在发泡过程中，由于重力和黏性力的影响，使泡沫骨架产生拉伸和变形[15]。而对于泡沫结构各向异性的描述，常用各个方向的孔径长度比值进行定量表征[5,16]。在不考虑孔内介质的条件下，Iasiello等[8]采用形态学分析，统计出3个正交方向的胞元直径，以高斯分布的中值作为各向异性的表征量。此外，采用COMSOL Multiphysics计算3个正交方向的等效导热系数。结果表明，结构各向异性与导热各向异性正相关。当考虑孔内流体流动时，Iasiello等[17]发现，当骨架自身为热源对孔内流体进行加热时，拉伸方向的传热系数最小，说明传热各向异性不仅与结构各向异性有关，也与边界条件强相关。

上述关于各向异性的研究主要是针对真实结构的，然而，真实结构无法控制孔隙结构参数，无法有效对结构进行设计和优化。在此基础上，本团队[18]结合Dai等[12]的各向同性Kelvin泡沫理论模型和Iasiello等[8]的各向异性结构表征，通过理论推导，建立了各向异性Kelvin泡沫等效导热系数理论预测公式，并且将理论预测结果和真实结构的数值计算结果进行对比，发现两者吻合良好，进一步定量证明了导热各向异性与结构各向异性正相关，并且指出Kelvin泡沫拉伸方向的导热系数最大，且最大值数值可达到胞元最短方向等效导热系数的1.47倍。

根据以上表述，如果将沿主流方向的尺寸作为直径，加热方向尺寸为高度，Kelvin泡沫的各向异性可用不同胞元高径比来表征。胞元高径比的改变影响各向同性Kelvin泡沫的传热特性，那么是否可利用胞元高径比去设计和优化各向异性Kelvin的传热特性？对于该问题，Sun等[19]已经开展了部分工作，将Kelvin泡沫沿通道主流方向拉伸1.5倍和2.0倍，此时，胞元高径比分别为2/3和1/2，最终结构的比表面积随着胞元高径比的减小而增大。在数值计算中，与Iasiello等[17]的边界条件相同，骨架自身为热源对孔内流体进行加热，分析不同速度下胞元高径比为1、2/3、1/2时Kelvin泡沫内的流动传热特性。结果表明，胞元高径比为1/2时的导热系数最低，传热系数与Kelvin泡沫比表面积成反比。该现象似乎与传统认知相反，事实上，主要原因是Sun等的研究更偏向于工程应用，在计算中保持速度大小一致，在该条件下胞元高径比越小，流道高度越低，导致雷诺数较低；而导热系数随着雷诺数的增大迅速增大，特别是在非达西区，Sun等[19]的计算又刚好位于非达西区。此外，Sun等未考虑骨架自身的导热，将流-固边界定义为等热流边界，只对孔隙中流体的流动传热进行数值模拟。事实上，在实际工程应用中，骨架的导热增强是十分重要的。因此，在同时考虑泡沫骨架导热和Kelvin泡沫内孔隙尺度强迫对流换热的共轭传热时，胞元高径比对传热性能的影响可在保持雷诺数一定的条件下作进一步分析。

基于上述问题和现状，本研究在保证流态相同的条件下，以各向异性Kelvin泡沫为研究对象，开展不同胞元高径比对各向异性Kelvin泡沫流动传热特性的影响研究，着重分析胞元高径比变化对流动传热内在影响机制，为飞行器热管理系统中泡沫结构设计提供技术支撑。

1 Kelvin泡沫几何参数

本文选择如图1所示的5种不同泡沫进行研究。其中，Kelvin泡沫的长度x和宽度z保持一致，记为Kelvin泡沫的直径，其尺寸均为D。高度H（y）与直径D之比H/D则定义为胞元高径比。当胞元高径比H/D=1.0时，该结构为最为常用的各向同性Kelvin泡沫[20-22]。本文选取H/D= 0.5、0.75、1.5、2.0的各向异性Kelvin泡沫进行研究。

对于Kelvin泡沫，孔隙率是影响传热性能的主要参数之一，在本研究中孔隙率保持不变，因此通过调整Kelvin泡沫的韧带半径和节点尺寸，最终保证本研究的5种构型Kelvin泡沫的孔隙率ε均为0.912。此外，为了便于对比分析，保持流道方向长度D= 4 mm。经过上述尺寸设定，在孔隙率一定的条件下，5种构型Kelvin泡沫的比表面积αsf分别为1412.9、1189.2、1079.8、955.6、891.2 m2/m3，可以看出，随着H/D不断增大，比表面积不断减小。表1给出了5种Kelvin结构的结构参数。

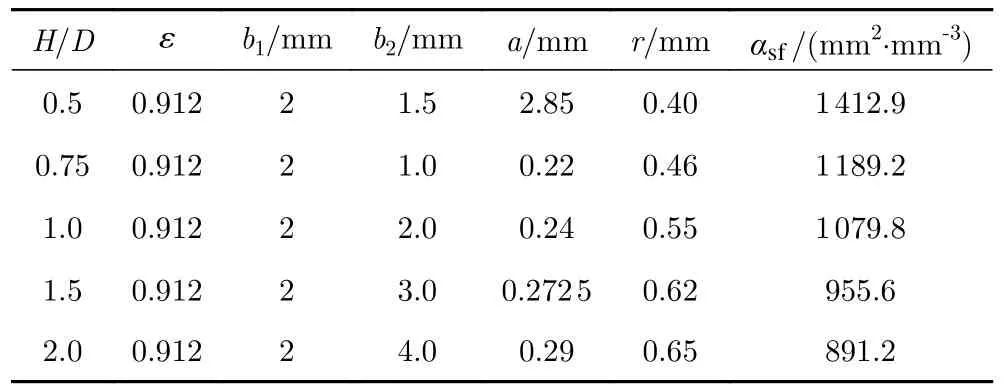
表1 Kelvin泡沫几何参数Table 1 Geometrical parameter of Kelvin structure

2 计算模型与方法

2.1 计算模型

本文采用如图2所示的计算模型，参考Iasiello等[16]的研究，沿通道方向布置4个Kelvin泡沫，其尺寸为 4D×D×H，流体通道的整体尺寸为Lx×Ly×Lz=6D×D×H。其中，通道沿y方向的高度分别为0.5D、0.75D、1.0D、1.5D、2.0D。Kelvin泡沫设置为导热体，其导热系数为ks，W/(m2·K)；通道流体的导热系数为kf，W/(m2·K)。此外，4个Kelvin泡沫的上壁面为加热面，保持高温Th，K；左壁面为进口，进口冷却流体的温度为Tc，K，速度为u0，m/s；右壁面为出口，设为压力出口边界；前后壁面为对称面，其余壁面保持绝热。

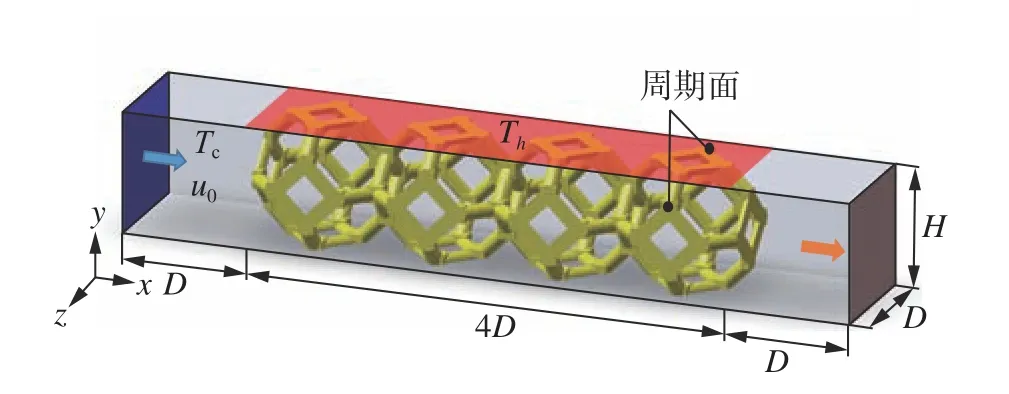
图2 计算模型示意图Fig.2 Schematic of numerical model

在对流动传热特性进行分析之前，需要控制一些变量以保证流动及传热特性相似。对于本文的强迫对流问题，最重要的参数是雷诺数。对于该结构，通常选取流道高度H为参考长度，其雷诺数的表达式为：

式中 υ为动力黏度，Pa·s。为了保证流动相似（即Re相同），对于不同胞元高径比结构，需要设置不同的初速度。

2.2 计算方法与流程

本文计算采用混合热格子Boltzmann法（hybridthermal lattice Boltzmann method, HTLBM），即流场采用多松弛格子Boltzmann法（multi-relaxation time lattice Boltzmann method, MRT-LBM），温度场采用有限差分法（finite difference method, FDM）。

2.2.1 流场计算

MRT的演化方程为[23]：

其中：r为空间坐标系；δt为时间步长；f是速度空间的密度分布函数；M是N×N阶转化矩阵，用于将f从速度空间线性地转化为矩空间的m；S是非负的松弛矩阵；m和meq是矩空间的分布函数和平衡态分布函数。m、f和M之间的关系满足：

其中，m、f和meq的表达式为

本文采用D3Q19模型，其转化矩阵M为：

转换后，矩空间内m和meq分别为：

其中松弛系数的取值为：se=sε=sπ=sv=1/τ,sm=sq=8(2-sv)/(8-sv)。

对于流-固边界，采用LBM反弹格式进行处理。本文采用均匀笛卡尔网格进行数值计算，流-固边界与坐标点无法保证完全重合，直接反弹会产生一定误差，因此通过提高网格规模来降低边界格式带来的误差，最大计算网格数达1.16亿。

2.2.2 温度场计算

对于流体域，无内热源、常物性稳态流体对流-扩散方程：

其中，αf为流体热扩散系数，m2/s。采用以下参数进行无量纲处理：

得到：

分别采用二阶迎风和中心差分格式离散式（11）中的对流项和扩散项：

其中：

式（13）中：

式（14）中：

时间项采用二阶显式Runge-Kutta方法进行离散：

式中，n为计算时刻点。

固体域的能量方程，即骨架导热方程如下：

其中αs为固体域热扩散系数，m2/s。时间项和扩散项离散方式与流体域相同，不再赘述。

对于流-固边界，为了和流场计算边界进行统一，不再对边界进行单独建模，采用虚拟节点来表示流-固界面，如图3所示。图中，（s,i）和（f,i）为同一节点，即s-f为虚拟点。通过上述定义，流-固界面的离散方程为：

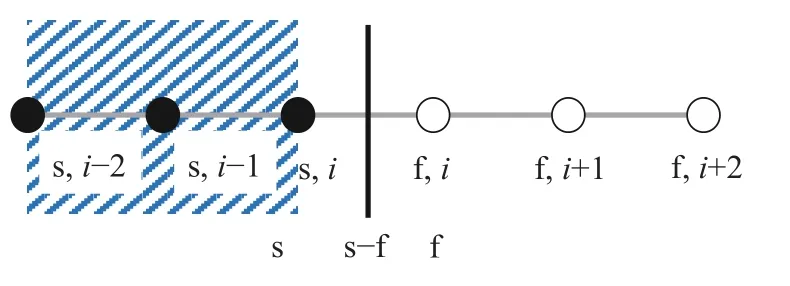
图3 流-固边界示意图Fig.3 Schematic of fluid-solid boundary

其中，kr=ks/kf，ks和kf分别为Kelvin泡沫骨架和流体的导热系数。

2.2.3 计算流程

对于含有多孔介质的复杂流动、传热和结构导热的多场耦合问题，采用如图4所示流场和温度场同步求解的方法进行数值计算，即流场和温度场采用相同的时间步长。此外，复杂结构（图1）的网格划分及边界识别方法可参考之前的研究[18]，这里不再赘述。

图4 计算流程图Fig.4 Flow chart of numerical simulation

为了充分发挥LBM天然并行性的优势，采用4张Tesla A100 GPU卡并行加速，网格数最大为1.16亿，可获得2153.5 MLUPS的计算效率。

2.3 流动传热特性参数定义

对于该类问题，衡量流动特性的参数有很多种，应用最为广泛的是流道进出口压降、渗透率和摩擦系数。

进出口压降的计算公式为：

式中，pin和pout分别为进口、出口压力，Pa。

由于压降的方向是沿流动方向，所以渗透率同样沿流动方向进行计算。根据达西定律，渗透率的表达式为：

其中，Kf为渗透率， µm2；υ 为动力黏度，Pa·s； 〈ux〉为沿流道流过泡沫的平均速度，m/s； ∇p为压力梯度，Pa。

对于本研究，采用LBM进行流场求解，因此，以x方向为例，最终的渗透率计算公式为[24]：

其中，Lf为通道长度，m；Nf为Lf长度对应的格子点数。

摩擦系数的定义如下：

其中， ∆p为 压差，Pa；Dh为水力直径，m，在本文中，流道截面为正方形，水力直径等于流道截面的边长Lf；其中， 〈ux〉的求解见公式（22）。

为了定量化地表征泡沫材料在不同方向的传热性能，定义换热系数h和体导热系数hv如下：

其中，q为热流密度，W/m2；Th为加热面温度，K；Tf为泡沫材料内部平均温度，K。

此外，泡沫结构需要保持高导热系数和低压降。然而，当hv很高时，泡沫结构总是伴随着高压降。因此，需要对这些参数之间进行权衡，既满足传热需求，又在合理的压降范围。一些学者采用综合评价指标j/f1/3来衡量泡沫结构综合性能指标。

其中，j为Colburn因子，Nuv为努塞尔数：

病史摘要:患者17岁,因“反复下腹胀痛1月,加重3天”入院。患者12岁初潮,月经基本规则,量中,伴痛经。近1月反复出现下腹胀痛,可忍受,伴腰痛,无异常阴道流血流液,自行购买止痛药物后缓解。3天前患者自感上述症状加重,伴发热,遂来我院门诊就诊。未婚有性生活1年,未孕。

2.4 程序验证

为了验证本文数值计算方法，采用如图2所示的计算模型进行数值验证。其中，Kelvin泡沫胞元高径比选为1。为了与Xia等[25]的实验结果进行对比，Kelvin泡沫骨架为铜，流体为空气。本文计算结果和文献对比结果如图5所示。结果表明，整体上看，本研究的计算结果与文献中的结果整体上吻合良好，但在局部存在一定差异，与Xia等[26]的实验最大相对误差为7.63%。主要原因是本文采用的是Kelvin结构，而Xia等[25]采用的是真实泡沫铜，两者微细结构存在一定差异。

图5 体传热系数hv计算值与实验值的对比Fig.5 Comparison of calculated and experimental values of body heat transfer coefficient hv

2.5 网格无关性验证

由于本文中的模型尺寸不相同，在计算中分别对H/D= 0.5、0.75、1.0、1.5、2.0五组模型在Re= 1000的工况下进行网格无关性考核。结果如表2所示，表中采用不同条件下的高度H的网格数为参考。从表中可知，对于H/D= 0.5、0.75、1.0、1.5、2.0的五组模型，当高度方向的网格数分别达到154、140、156、206、182时，hv不再受网格变化的影响，因此，H/D= 0.5、0.75、1.0、1.5、2.0时， 高度方向的网格数分别取154、140、156、206、182。

表2 不同 H/D 和 高度方向网格数下的hvTable 2 The value of hv in different grids andH/D

3 结果与讨论

本文在Sun等[20]的研究基础上，重点分析Kelvin泡沫胞元高径比对其流动传热特性的影响。与Sun等的研究不同的是，本文不仅保持了相同的雷诺数，而且考虑了多孔介质的复杂流动、传热和结构导热的多场耦合，同时分析了结构参数Kelvin泡沫胞元高径比的变化对流动传热的影响。相比较于Sun等的研究，本文的研究更全面地考虑了多种因素对流动传热的影响。

3.1 流动特性分析

图6为Re=100 时、不同H/D下的流线图。从图中可以看出，随着H/D的不断增大，流线分布逐渐均匀，即骨架柱体对流线的扰动越来越小。特别是在通道的尾端，当H/D=0.5时，尾端流线受骨架的扰动发生明显偏转，但当H/D增大到2.0时，这种偏转现象变得平缓，流线逐渐变得平直。原因主要是骨架柱体对流体的扰动程度主要受压力和雷诺数的影响，随着流通面积的逐渐增大，相同流态下（Re相等），压差变得越来越小。为了进一步分析，沿流道中心（y=0.5H，z=0.5D），取三种条件下的压力沿x方向的分布如图7所示。为了便于比较，采用通道长度6D对x进行无量纲化。

图6 不同H/D 时的流线图Fig.6 The streamlines at different H/D

图7 H/D = 0.5、1.0、2.0时流道中心（ y = 0.5H、z = 0.5D ）上的压力随x的变化Fig.7 Variation of pressure on the center of the flow channel(y = 0.5H and z = 0.5D) with x at H/D = 0.5, 1.0, 2.0

从图7中可以看出，在x方向的相同位置，以进口压力为参考，随着H/D的不断减小，压差逐渐增大。此外，在骨架位置压差的分布呈周期性下降，取一个单胞分析，H/D= 0.5、1.0和2.0时的压差分别为0.00066p0、0.00135p0和0.00374p0。H/D从2.0减小到0.5，压差增大55.67倍。因此，该结果也进一步解释了图6中，流线由不均匀分布转为均匀分布的原因。此外，H/D=2.0时，压力随着x增大是连续下降的，骨架喉道区域的前端压力几乎不变，尾部是产生压降的主要部位。随着H/D减 小，特别是H/D=0.5时，压力随着x增大在骨架的喉道区域出现明显的脉动，尽管产生压降的主要部位仍位于喉道的尾部，但最大压力同样为喉道的尾部区，说明喉道尾部发生明显阻塞。当H/D=2.0时，喉道前中部位置的压力几乎不随x的增大发生明显变化，当H/D减小到0.5时，喉道前中部的压力随x的增大出现先减后增的趋势。产生该现象的主要原因是尾部的阻塞使得前部压力降低，当流体流过喉道区域，流道的扩张使阻塞效应变小，使得流体压力降低。而使压力产生波动的主要原因是随着H/D的减小，喉道内Kelvin泡沫顶部骨架和底部骨架的距离减小，骨架间流体的相互扰动也随即增大，使得压力沿流道方向的分布不再均匀。

图8为不同H/D时z=0.5D截面上的无量纲速度分布云图。在前文中提到，为了保证流态相似，在计算过程中保持雷诺数不变，因此无量纲速度的范围保持一致。可以看出，z=0.5D截面上的速度分布随着H/D的减小发生明显的变化。图中红色区域为流速较高区域，不同H/D时，其分布形状均近似为三角形。随着H/D的减小，喉道进口位置的高度越来越低，三角形逐渐被压扁，由近似为等边三角形变化为明显等腰的锐角三角形，且流道方向的锐度也越来越大，原因主要是喉道进口处出现的阻塞效应随着喉道高度的减小而增大。此时，流体在喉道进口处被挤压的强度最高，因此，相同喉道长度下，压差随着H/D的减小而增大，导致高流速区域面积占比增大。此外，定义等腰三角形的底角为 θu，如图8所示。

表3 不同H/D时的θuTable 3 The value of θu at different H/D

图9 流道中心（y = 0.5H、z = 0.5D）上的速度沿x分布Fig.9 Distribution of velocity along x at H/D = 0.5, 1.0, 2.0

为了进一步分析流场的分布特性，图10给出了不同H/D时z=0.5D截面上的无量纲涡量分布。从图中可知，除了流道进口位置外，对称涡主要存在于各个喉道的进出口位置，其余仅在H/D= 0.5时，在结构的每个骨架的迎风面形成明显的对称涡。

图10 H/D = 0.5、0.75、1.0、1.5、2.0时，z = 0.5D截面上，无量纲涡量分布云图Fig.10 Dimensionless vorticity distribution on z = 0.5D surface at H/D = 0.5, 0.75, 1.0, 1.5, 2.0

与流场特性相似，在喉道位置涡中心线与竖直方向夹角发生明显变化，定义该夹角为 θω，如图10所示。不同H/D条 件下的 θω如表4所示，与速度场中的 θu相似，随着H/D的 减小， θω也逐渐增大，增大的趋势也较为接近。

表4 不同H/D条件下的θωTable 4 The value of θω at different H/D

对于该类Kelvin泡沫，无量纲参数D2/Kf是评价其流动特性的重要参数，其表达式中运用了渗透率的倒数，D2/Kf越小，Kelvin泡沫的渗透性越好，因此认为D2/Kf可表征流经Kelvin泡沫产生的阻力特性。为了更好地对比不同H/D条件下的渗透特性，分别计算Re=10 、 100、1000条件下的D2/Kf，如图11所示。不同Re条件下，D2/Kf均随着H/D的增大而减小，表明随着H/D的增大，渗透性越好，主要原因是随着H/D的增大，Kelvin泡沫沿着高度方向被拉伸，流动截面逐渐增大，压差逐渐减小，流动阻力越来越小，渗透性也就越来越好；相同H/D条件下，D2/Kf随着Re的增大而增大，表明流速越大，相同结构下流动阻力越来越大，骨架的渗透性越差；随着H/D的增大，不同Re间D2/Kf的差异减小，表明H/D和Re对D2/Kf的影响均是非线性的。进一步说明，对于各向异性Kelvin泡沫，结构参数H/D与流态表征Re在实际工程设计中均不可忽视。

图11 不同Re下D2/Kf随H/D的变化Fig.11 The change of D2/Kf with H/D at Re = 10, 100 and 1 000

3.2 传热特性分析

3.1节中重点分析了Kelvin泡沫H/D对其流动特性的影响，本节将重点分析H/D对传热特性的影响。

图12为Re=100 条件下，H/D= 0.5、1.0、2.0时，Kelvin骨架表面温度分布以及3个方向中截面温度分布。由于3个样品的高度不同，选择同一位置的单个细胞进行相互比较具有一定的局限性[20]，因此在进行骨架对比分析时选择4个胞元。3种样品的骨架温度分布相似，温度较低的部位主要位于流速较高的喉部。此外，当H/D=2.0时，由于顶部骨架背风处存在明显的低速区，该区域的空气温度高于胞元其他区域。当H/D=0.5时，背风区域减小，低温区域不仅位于喉部位置，骨架通道位置也形成明显的低温区。

图12 Re = 100时Kelvin骨架表面以及x 、y 、z 方向中截面温度分布：（a）H/D = 0.5；（b）H/D = 1.0；（c）H/D = 2.0Fig.12 The temperature distribution on the surface of the Kelvin skeleton，and middle sections in x, y and z directions at(a) H/D = 0.5，(b) H/D = 1.0 and (c) H/D = 2.0 when Re = 100

为了进一步分析上述现象，给出不同H/D条件下，z=0.5D截面上的温度分布如图13（a）所示。随着H/D的增大，骨架底部区域的温度场差异较小，但顶部区域的差异较为明显。顶部区域的差异主要体现在以下3个方面：

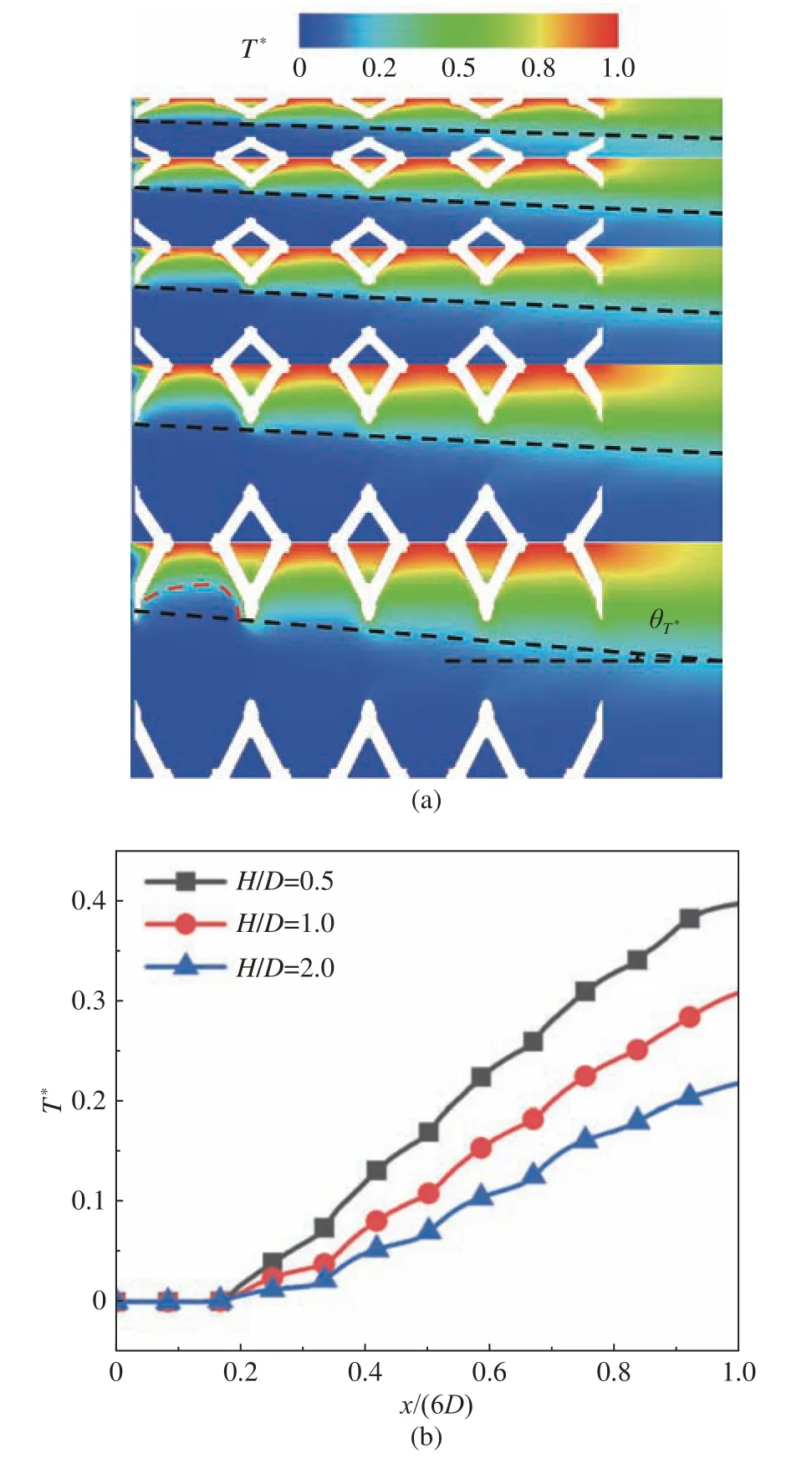
图13 Re = 100时，（a）不同H/D下，z = 0.5D截面的温度分布；（b）H/D = 0.5、1.0、2.0时流道中心（y = 0.5H、z =0.5D）温度沿x的分布Fig.13 Re = 100, (a) The temperature distribution on z = 0.5D surface under different H/D; (b) Temperature distribution of the center of the flow channel (y = 0.5H and z = 0.5D) along x at H/D= 0.5, 1.0 and 2.0

首先，喉道前部位置，当H/D= 0.5时，骨架迎风面几乎无高温区域，随着H/D的增大，骨架沿高度方向的长度增大，迎风区域骨架边缘的温度明显降低；与此同时，骨架背风区域的低温区域占比变大，原因是背风区域形成了明显的低速区，导致传热性能降低。

其次，在喉道的中间区域，当H/D为0.5时，在第一个骨架区域，等温线与主流方向几乎平行，但随着H/D的增大，等温线形成了明显的拱形且凹面向下分布（图13（a）中红色虚线）。该现象说明胞元高径比H/D影 响了传热主导方式。当H/D=2.0时，由于背风面存在流动低速区，导致强迫对流换热强度较小。由于骨架和流体的导热系数比为1000，骨架导热起主导作用，热量优先沿骨架传递，因此骨架周边的温度明显高于四周，等温线在上部区域形成明显的拱形；但当H/D减小到0.5时，背风面的低速区域明显减小，此时，强迫对流占主导，拱形区域逐渐消失；但在单胞尾部喉道位置，H/D=2.0时的骨架周边温度却高于H/D=0.5时的温度。为了进一步定量分析这种现象，引入场协同理论，对于对流传热问题，场协同角 β的表达式为：

根据场协同理论， β是流动方向与温度梯度方向的夹角， β越小传热性能越优。H/D=0.5和2.0时，z= 0.5D截面上Kelvin泡沫区域的场协同角分布如图14所示。重点关注通道上部区域，单喉道前部位置（图14中黑色虚线标记），H/D=0.5 时 的 β明显小于H/D=2.0 的 β。与之相反的是，单喉道尾部位置（图14中红色虚线标记），H/D=0.5 时 的 β 明显大于H/D=2.0的 β，这就可以解释为何Kelvin泡沫前部和尾部喉道位置，H/D=0.5和2.0时的温度分布呈现明显差异。

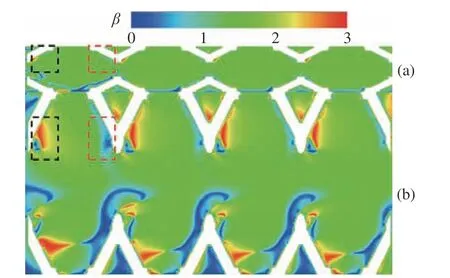
图14 Re = 100时，z = 0.5D截面上Kelvin泡沫区域的场协同角分布：（a）H/D = 0.5；（b）H/D = 2.0Fig.14 The distribution of field-synergy angles on the z = 0.5D surface of the Kelvin structure for (a) H/D = 0.5 and (b) H/D = 2.0 with Re = 100

最后，高温区域与主流方向的夹角呈现明显差异。为了便于对比，取通道尾部温度为0.3向通道进口连线（图13（a）中黑色虚线），对通道的高温区域和低温区域进行近似划分。取分界线与主流方向夹角为 θT∗，如图13（a）所示。从图中可以看出， θT∗随着H/D的增大而增大；与之相反的是，高温区域面积占比随着H/D的增大而明显减小。

为了进一步定量分析，沿流道中心（y=0.5H，z=0.5D），取三种条件下（H/D= 0.5、1.0和2.0）的无量纲温度沿x方向的分布如图13（b）所示。从图中可以看出，三种条件下，温度沿x方向的变化趋势相类似，呈明显的波动特性。在每个单喉道内，三种条件下温度曲线发生波动的位置保持一致，分别位于喉道进口、中间位置和喉道尾部位置。此外，除了进口位置，H/D=0.5 时 温度最高，随着H/D的增大，温度越来越低，这与图13（a）中高温面积增大的原因相同，主要是喉道高度变低，流动由骨架导热主导变为对流传热占主导，使得对流传热性能提高，中心位置的温度升高。对流传热性能的提高也会导致整体喉道前部温度升高，这也是 θT∗降低的原因，因此随着H/D的增大，Kelvin泡沫的传热性能逐渐降低。为了进一步验证，根据公式（27），计算不同H/D条 件下的Nuv如图15所示。

图15 Re = 10、100、1 000时Nuv和αsf随H/D的变化Fig.15 The change of Nuv and αsf with H/D at Re = 10, 100, 1 000

从图15中可以看出，在三种Re条件下，Kelvin泡沫的Nuv均随着H/D的 增大明显降低，并且，Nuv随H/D的 变化曲线是非线性的。与此同时，随着H/D的增大，不同Re之间Nuv的差异越来越大。H/D从0.5增大到2.0，Re=10 、 100和1000时，Nuv分别降低77%、80%和84%，说明Re越大，H/D对Nuv的影响越大。此外，图15给出了不同H/D条件下的比表面积。从图中可知，随着H/D的增大，比表面积减小，这与Nuv随H/D的变化规律保持一致。对于多孔介质材料，比表面积越大，流-固界面换热效率越高，这也可进一步解释Nuv随着H/D的增大而降低的原因。

通过前述分析可知，对于不同H/D的Kelvin泡沫而言，降低H/D能很大程度上提高传热效率，但与此同时会使流动阻力增大。因此，需要采用综合评价指标对该问题作进一步分析。 本文采用常用的j/f1/3（见公式（26））来评价流动传热性能，不同H/D条件下的j/f1/3如图16所示。从图中可以看出，相同H/D条件下，随着Re的增大，j/f1/3减小，这与Sun等[19,26]以及Yang等[9]的结果一致。此外，在不同Re条件下，随着H/D的 增大，j/f1/3也减小，与图15中Nuv的变化趋势相同。结果表明，尽管H/D的增大使得流动阻力减小，但Nuv的降低占主导地位，使得综合评价指标j/f1/3减小，因此整体上看，降低Kelvin泡沫胞元高径比有利于结构的综合传热性能。

图16 Re = 10、100、1 000时，j/f 1/3随H/D的变化Fig.16 The change of j/f 1/3 with H/D at Re = 10, 100 , 1 000

4 结 论

本文以各向异性Kelvin泡沫为研究对象，分析了其胞元高径比对流动传热特性的影响，主要结论如下：

1）不同Re下，各向异性Kelvin泡沫流动阻力（D2/Kf）及努塞尔数（Nuv）均随着胞元高径比（H/D）的减小而增大。当Re= 10、100和1000时，D2/Kf分别增大203%、208%和305%，Nuv分别增大77%、80%、84%。尽管不同Re下流动阻力增大的百分比均大于Nuv增大的百分比，但综合传热因子j/f1/3仍随着H/D的减小而增大，即小胞元高径比的Kelvin泡沫具有更好的综合传热性能。

2）不同H/D下 ，综合传热因子j/f1/3随着Re的增大而减小，表明Kelvin泡沫在低雷诺数下的综合传热性能更优。

3）本研究在考虑泡沫骨架导热且保证雷诺数一定的条件下获得的规律与Sun等[19]不考虑骨架导热且保持速度一定时得到的结果完全相反，表明骨架导热和Re是该类问题中不能忽略的重要影响因素。

本研究假设飞行器在无重力环境下服役，未考虑重力的影响。实际上，在一些情况下，如在飞行器起落和在微重力环境下飞行时，重力的方向和大小对流动传热的影响不可忽略，这也是作者下一步的研究工作。