结合机器学习与高光谱遥感的城市内河水质反演

曾江超, 黄风华, 李秉政, 高荣刚

(1. 福州大学数字中国研究院(福建), 福建 福州 350108; 2. 福建省空间信息感知与智能处理重点实验室(阳光学院), 福建 福州 350015; 3. 空间数据挖掘与应用福建省高校工程研究中心(阳光学院), 福建 福州 350015)

0 引言

水环境治理的前提是准确获取水体的健康状况, 进而及时调整治理策略, 保障水体质量健康稳定[1]. 总磷(TP)、 总氮(TN)是评价水体富营养化的重要指标, 主要来源是化肥和洗涤废水排放, 研究这些指标对于监测和治理河流水体富营养化有着重要意义[2].

由于内陆水体成分复杂多样, 多光谱遥感探测水体的光谱信息较弱[3]. 而高光谱遥感带来了丰富的光谱信息, 能够提高内陆水体水质参数的反演精度[4]. 再者城市内河宽度较窄、 水网密集, 因此空间分辨率更高的无人机影像成为内河水环境监测的首选方案[5].

目前, 利用卫星和无人机高光谱影像的水质反演已有大量研究[6]. Wang等[7]基于地貌学的非点源污染模型分析了长江干流TN浓度及其对水质的影响, 但是此类半经验模型的泛用性不高. Cao等[8]采用极端梯度增强树对中国东部湖泊进行水质反演, 证明了机器学习算法在水体监测的潜力. Chen等[9]采用随机森林回归(RF)对墨西哥湾进行TP、 TN的反演, 结果表明RF算法能卓越处理此类非线性问题. 盛辉等[10]采用改进的支持向量回归(SVR)对潍河水域取得了较好的反演效果, 并在山东半岛峡山水库测试了该模型的泛化能力. 以上研究均表明, 采用机器学习算法进行水质反演具有较高的可行性.

本研究基于高光谱相机采集的影像, 利用机器学习算法, 结合福建省福州市晋安河的实测光谱数据, 进行TP和TN模型构建和水质反演, 从而既能丰富城市内河水质遥感反演的理论研究, 又可对内河的水体富营养化监测提供重要参考价值.

1 材料与方法

1.1 研究区概况

福建省福州市晋安河历史悠久, 贯穿晋安区、 鼓楼区和台江区, 其河流水质的好坏直接影响福州市的整体市容市貌和居民生活. 因此本研究选择晋安河为研究区, 由于研究区域长度将近7 km, 整条河流水质反演图效果不直观, 所以仅展示图1晋安河东门村河段(26.09°～26.10°N, 119.310°～119.312°E)约800 m的水质参数反演结果.

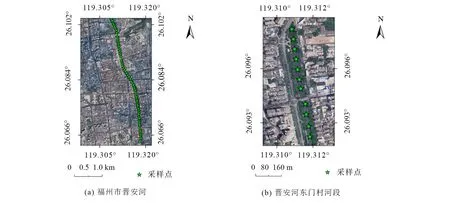
图1 研究区与采样点示意图Fig.1 Schematic diagram of study area and sampling points资料来源: 水经微图(图幅号G50H092170, G50H092171, G50H093171)http://www.rivermap.cn/

1.2 水质参数样本采集

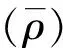
表1 晋安河取样点实测水质数据统计

1.3 水面实测光谱数据采集

由于此次无人机航飞晋安河采用的高光谱相机波段范围为400～1 000 nm, 波长总数为176个, 故使用Field Spec4手持光谱仪在波段为400～1 000 nm内按照3.4 nm间隔采样. 在标准取水器采水之前, 使用手持光谱仪采用45度倾斜法采集采样点处水面光谱信息, 单个采样点重复采集5次, 均值作为水体反射值, 每次测定前需要采集自然光和灰板数据用于数据校正. 图2为实测数据绘制的光谱反射率曲线, 其中波长用λ表示, 反射率物理量用R表示.

图2 样本点处实测光谱信息 Fig.2 Measured spectral information at sample points

1.4 无人机高光谱影像采集与处理

根据研究区域的地形制定对应航线, 通过DJI M600 Pro六旋翼无人机搭载双利合谱GaiaSky-mini2高光谱相机获取晋安河高光谱影像, 光谱范围为400～1 000 nm, 光谱分辨率和空间分辨率为8 nm和0.32 m. 由于较强的水汽吸收, 波长大于900 nm时信噪比低, 反射率波动较大, 故反演建模和可视化时选择400～900 nm波段. 而且无人机高光谱影像反射率振幅大, 本研究采用Symlet小波变换对无人机高光谱影像各像素点反射率进行处理[13]. 其中选用sym8作为小波基, 并采用5层小波分解进行去噪. 去噪前后结果如图3所示. 小波变换公式为

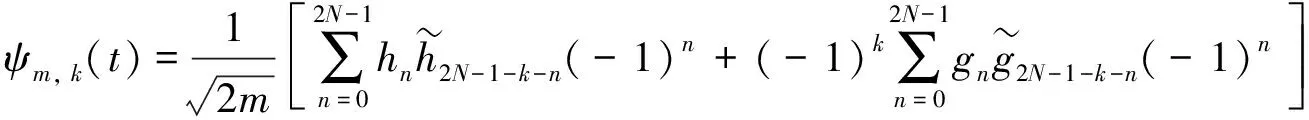
(1)

图3 影像去噪前后结果Fig.3 Results before and after denoising of image

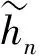
1.5 研究方法

1.5.1波长筛选和处理算法

1) 连续投影算法(SPA)是一种降维算法, 从光谱变量中找到冗余信息最少的变量组合. 该算法通过将波长投影到其他波长上, 比较投影向量大小, 以投影向量最大的波长为待选波长, 然后基于矫正模型选择最终的特征波长[14].

2) 皮尔逊相关系数(Pearson)可以反映两个变量的线性相关程度, 本研究主要是筛选出能用于各水质参数反演波长和波长组合.

采用方差膨胀因子(VIF)主要是为了避免使用相似作用的因子, 减少模型的误差. 当该值大于10时, 则说明多重共线性较强, 需要舍弃.

3) 大量研究表明, 对两种及以上波长进行组合计算, 可以降低部分外界干扰, 增强有效的光谱信息, 从而增大模型的拟合度. 因此, 本研究构建了双波长差异指数(ID)、 比率指数(IR)和归一化差异指数(IND)模型对波长进行处理. 即

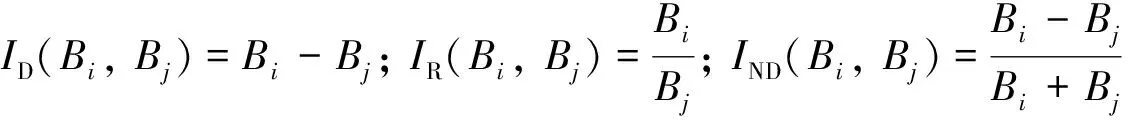
(2)

式中:i=1, 2, …, 176;j=1, 2, …, 176;Bi和Bj表示无人机遥感影像的波长值.

1.5.2机器学习算法和评价指标

1) 采用机器学习算法如随机森林回归(RF)、 支持向量回归(SVR)、 KNN回归(KNN)、 Adaboost回归算法建模. 机器学习算法部分均采用Sklearn库, 其中SVM采用的是径向基核函数, 并采用GridSearchCV库进行调参. AdaBoost的基本思想是通过多次迭代, 将若干个弱分类器组合成一个强分类器[15].

2) 评价指标为决定系数(R2)、 平均相对误差(EMR)和均方根误差(ERMS). 其中:R2值在0～1之间, 相当于分类问题的精度, 其值越高越好;EMR用来衡量估计值与真值的相对误差百分比;ERMS用来衡量估计值与真值之间的偏差. 即

(3)

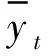
2 实验结果与分析

2.1 相关性分析

1) 各水质间的相关性. 由于TP、 TN水质参数对光谱不敏感, 因此参照李澜博士的处理方式, 计算TP、 TN与当天所采的其他9个水质参数的相关系数, 并将相关度较大的纳入反演模型自变量中[16]. 相关系数热力图如图4所示, 其中相关性大小用r表示. 由图中可知, TP、 TN与氨氮的相关性为0.70、 0.61, 说明氨氮 指标能影响TP、 TN质量浓度, 因此本研究尝试将影响氨氮的特征波长纳入TP、 TN水质反演中[16].

2) TP、 TN波长组合相关性分析. 选取晋安河86个样本点176波长, 逐波长遍历构建ID、IR和IND指数, 并计算其与TP、 TN浓度的皮尔逊相关系数. 水质参数与双波长指数相关性等值图如图5所示.

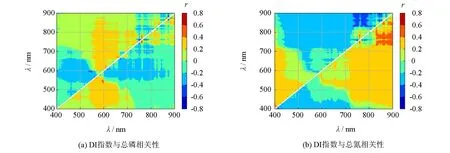
图5 相关性等值线分布图Fig.5 Correlation contour map

从图5可以看出, 采用ID指数对两两波长进行处理, 发现其与TP相关性最高接近0.8, 波长组合主要分布在600、 750 nm附近; TN与双波长ID指数相关性最高接近0.8, 相关性高的区域主要分布在800～900 nm之间, 相关性满足河流水质模型反演要求.

2.2 自变量筛选

由于高光谱数据原始波长数据量大, 自变量个数较多, 其中无关变量也多, 从而导致模型计算量大, 稳定性低. 因此采用合适的自变量是水质反演模型好坏的重中之重.

2.2.1SPA特征波长筛选

通过多次采用SPA算法设置不同阈值进行实验, 实验表明在样本数为86时, SPA迭代波长次数最高设置为20次. 同时将各波长反射率归一化(R′),R′范围为[-1,1], 模型效果较优. 如图6所示, 对总磷的波长进行筛选, SPA算法迭代到波长数为14时,RMSE处于最低值。最终总磷SPA选择888、 885、 404、 763、 899、 866、 401、 813、 827、 870、 670、 820、 475、 795 nm这14个波长; 总氮SPA选择763、 866、 728、 462、 813、 707、 401、 881、 578 nm这9个波长.

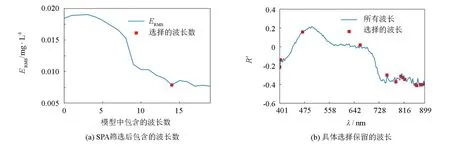
图6 SPA对总磷的特征波长选择Fig.6 SPA’s selection of characteristic bands for TP

2.2.2Pearson特征波长组合筛选

采用经验法选用Pearson系数较高的5个指数值(包括Pearson系数最高的ID、IR、IND各1个, 其余2个为所有Pearson系数最高的双波长指数)作为待反演水质模型的自变量, 同时采用VIF对这5个自变量进一步筛选, 剔除共线性强(VIF>10)的自变量,选出最终参与模型运算的双波长组合. 采用如上方法对TP、 TN和氨氮进行计算, 得到TP的双波长组合为ID(874, 867)、IR(750, 760)、ID(757, 760); TN双波长组合为ID(853, 860)、IND(670, 663); 氨氮双波长组合为ID(874, 867)、ID(767, 760)、IND(544, 600).

2.2.3最终采用的自变量

结合2.2.1与2.2.2, 晋安河TP、 TN反演最终采用的模型自变量如表2所示.

表2 各水质参数筛选的自变量

2.3 模型构建与精度评价

基于2.2.3所挑选的自变量作为模型训练的输入, 随机挑选70%样本点进行模型训练, 30%样本点进行测试. 采用10折交叉验证建立回归模型, 以决定系数(R2)、 平均相对误差 (EMR)、 均方根误差 (ERMS) 作为评价指标. 测试集对模型各指标检验结果如表3所示.

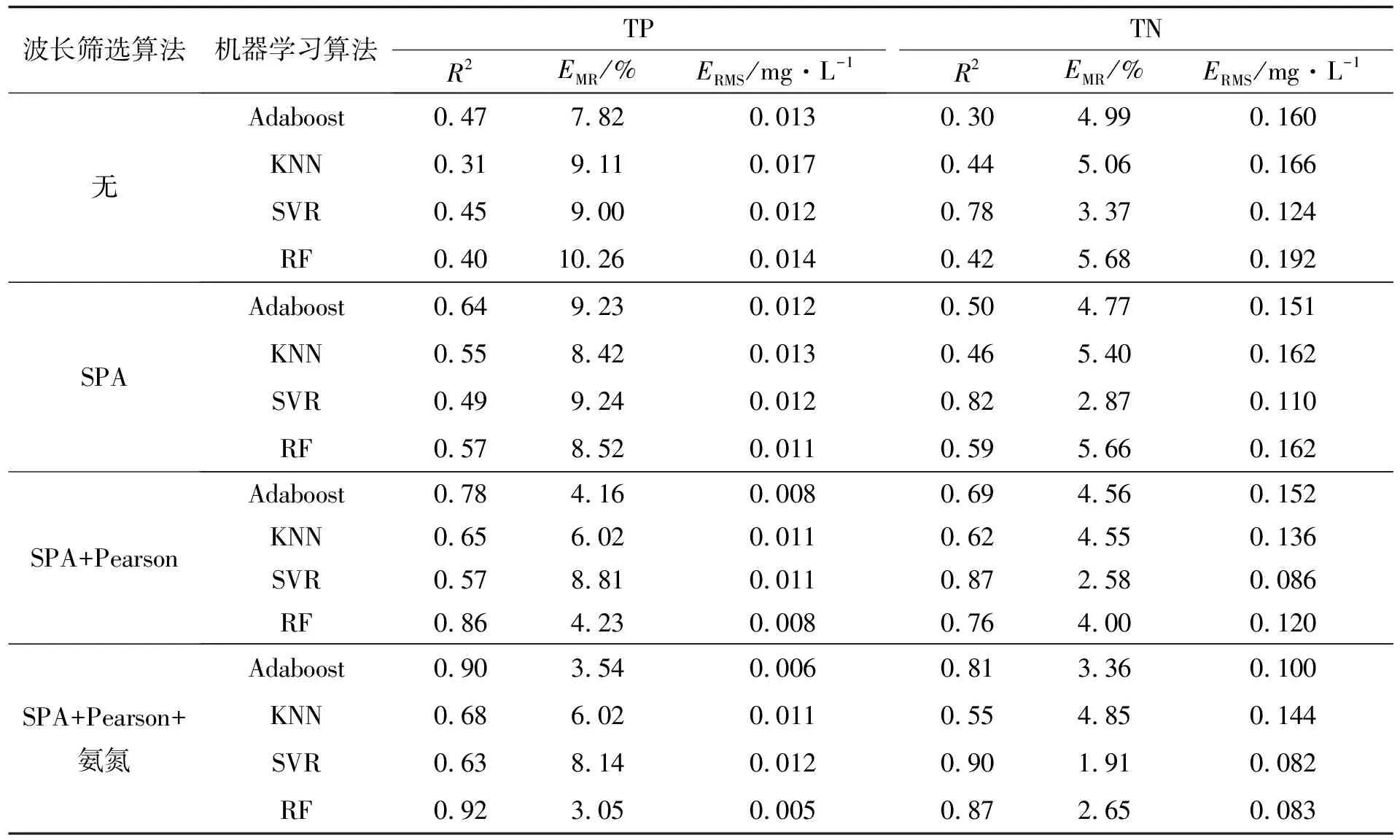
表3 各水质参数反演模型

由表3可知, 对于TP、 TN来说, 采用SPA+Pearson比SPA筛选算法模型的百分比偏差均有所降低,R2均有所提升, 这表明波长筛选算法结合的方式确实比单纯采用单波长建模效果更优. 并且将影响氨氮波长组合加入TP、 TN反演时, TP模型R2从0.86提升到0.92,ERMS从0.008 mg·L-1降低至0.005 mg·L-1, TN模型R2从0.87提升到0.90,ERMS从0.086 mg·L-1降低至0.082 mg·L-1, 模型的效果有所提升.

测试集最优模型验证图如图7所示. 其中TP、 TN反演模型R2均为0.9以上, 实验结果表明, 将SPA与Pearson波长筛选结合的方式, 同时考虑其他水质参数的影响, 可以取得较好的反演效果. 这对复杂内陆水体光学活性较差的水质参数反演有着借鉴意义.

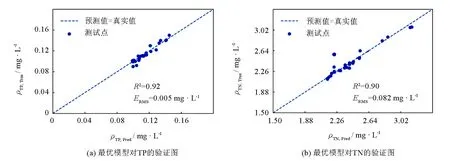
图7 晋安河最优模型与相应水质参数验证图Fig.7 Verification diagram of Jin’an River optimal model and corresponding water quality parameters

2.4 模型的泛化能力

采用福州市长乐区下洞江, 对SPA+Pearson+机器学习算法模型构建的TP、 TN模型泛化能力进行验证. 下洞江样本点数量为87, 数据分布如表4所示, 取其中70%作为训练集, 30%作为测试集. 实验结果如图8所示, 可以看出, 采用SPA+Pearson+氨氮的随机森林算法构建的TP模型决定系数R2为0.86,ERMS为0.032 mg·L-1, 采用SPA+Pearson+氨氮的SVR算法构建的TN模型决定系数R2为0.74,ERMS为0.450 mg·L-1. 结合晋安河实例, 该方法对下洞江的水质反演效果没有晋安河好, 其原因是下洞江水闸处于开放状态, 相较晋安河河流流速较快, 下洞江水质样本数据相对较差. 但尽管如此, 其水质反演效果仍旧良好, 这说明利用本研究提出的算法模型泛化能力不错, 能应用于其他河流水质反演之中.

表4 下洞江取样点实测水质数据统计

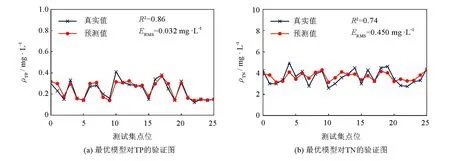
图8 下洞江最优模型与相应水质真实值和预测值验证图Fig.8 Verification diagram of Xiadong River optimal model and real-predicted value

2.5 反演结果

通过上述模型之间的对比, 选择最优模型对东门村河段无人机高光谱影像进行TP、 TN参数的反演可视化. 可视化结果如图9所示, 可以看出该河段TP质量浓度范围为0.09～0.14 mg·L-1, TN质量浓度范围为1.80～2.60 mg·L-1. 经现场调查发现, 河流两侧为居民地, 存在面源污染的情况, 其中左上角和左下角有两个居民排污口, 因此河流左侧相对桥下的TP、 TN浓度偏高, 从图中也可以明显看出这一趋势, 研究结果符合实地调研情况.

图9 东门村河段总磷和总氮反演图Fig.9 Inversion map of TP and TN in Dongmen Village reach

3 结语

本研究基于晋安河实测水质数据和光谱数据, 通过SPA算法对光谱波长降维提取, 并采用经VIF调整后的双波长Pearson相关性分析挑选出相关性强的波长组合, 之后再将与TP、 TN强相关的氨氮水质参数加入机器学习模型自变量中进行建模. 经测试集实测数据与模型预测结果的验证分析, TP、 TN两者最高模型R2均可达0.9,ERMS也相对较低, 同时在福州市下洞江对该方法模型进行验证, 实验表明模型拟合效果和泛化能力都较为出众. 最后采用最佳模型对晋安河东门村河段进行了TP、 TN的水质反演可视化, 结果表明, 各模型对无人机高光谱影像水质参数浓度反演的空间分布与东门村河段的实地调研情况基本符合.

目前采用无人机遥感进行水环境治理前景很大, 但季节性差异和区域性差异对河流水质的影响较大, 未来可以研究不同季节之间的模型差异, 从而进一步增强模型的泛化能力.