美国初中数学教科书中的中国数学史
王 彬,李春兰,张 涛
美国初中数学教科书中的中国数学史
王 彬1,2,李春兰1,张 涛3
(1.内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022;2.新惠中学,内蒙古 赤峰 024399;3.内蒙古师范大学 科学技术史研究院,内蒙古 呼和浩特 010022)
在研读分析21世纪初美国11本初中数学教科书的基础上,从栏目分布、内容分布和运用方式3个方面梳理了这些教科书中所融入的中国数学史内容.发现美国多本初中数学教科书中用精美别致的版面引入了中国数学史内容,如,勾股定理、负数、线性方程组、中国古代数学著作中的历史名题以及七巧板等内容.就美国初中数学教科书中融入中国数学史,得到5点启示:坚持立德树人,坚定对中华优秀传统文化的自信;追根溯源,求真求实;名题变式,以题说法;游戏数学,玩中传知;图文并茂,不乏趣味性和艺术性.
中国数学史;美国;初中数学教科书;历史名题;七巧板;民族自豪感;文化自信
1 问题提出
英国数学家格莱舍(J. W. L. Glaisher,1848—1928)说过:“如果企图将一门学科和它的历史割裂开来的话,我们确信,没有哪一种学科会比数学损失的更多.”[1]美国著名数学史家克莱因(M. Kline,1908—1992)主张:数学教材的编写者应该读一读历史上大科学家的有关著作,将教材写得更人性化一些[2].老一辈数学家余介石强调:“教师对于学理,必须考其在历史上发展之迹象,以觇人心认知之程序与限度,庶可因时指宜,善为说理,既不至使初学难以猝通,亦不至养成其谬见或误解.历史之于教学,不仅在名师大家之遗言轶事,足生后学高山仰止之思,收闻风兴起之效.更可指示基本概念之有机发展情形,与夫心理及逻辑程序,如何得以融合调剂,不至相背,反可相成,诚为教师最宜留意体会之一事也.”[3]国内外中小学数学教科书中融入数学史内容亦由来已久.例如:在美国数学教育家、美国数学会和美国数学协会的发起人史密斯(D. E. Smith,1860—1944)编写的教科书(《解析几何》,1922年)中介绍了解析几何的历史,数学家余介石编写、南京正中书局出版的《建国教科书高级中学平面解析几何学》(1936年)以该书为蓝本,融入了一定数学史内容;在段育华编写、上海商务印书馆出版的《新学制混合算学教科书初级中学用》第一至第六册(1923—1926年)中,共插入数学家肖像30幅(其中28位西方数学家,2位中国数学家),并附载小传;等等.
从19世纪末开始,美国数学史家和数学教育家们对数学历史的教育功能有颇多的阐述,包括激发学生的学习兴趣、改变学生的数学观、使数学人性化、让学生从原始文献汲取数学家的原始思想和社会文化信息、帮助学生更好地理解和欣赏数学、增强学生的自信心、通过历史可以了解学生学习数学的困难和认知过程等[2].《美国学校数学教育的原则和标准》中的课程原则强调,数学史知识可以作为“值得学生花时间和精力学习的数学内容”,它有助于“加深学生对数学作为一门学科和作为人类创造活动的理解”[4].在美国学者如此重视数学史的呼声下,美国初中数学教科书中融入了哪些中国数学史内容?是如何融入的?中华文化源远流长,积淀着中华民族最深层的精神追求,代表着中华民族独特的精神标识.在整个数学史的海洋中,中国数学史占有举足轻重的地位,中国古代数学体现算法化的优秀数学思想,在如今的数学教科书中,中国数学史内容必不可少.研究者选取2000年至2010年十年间美国初中数学教科书,不分版本,共查阅32本美国初中数学教科书,发现其中有11本(见图1、表1)教科书编有中国数学史内容.

图1 美国11本初中数学教科书书影
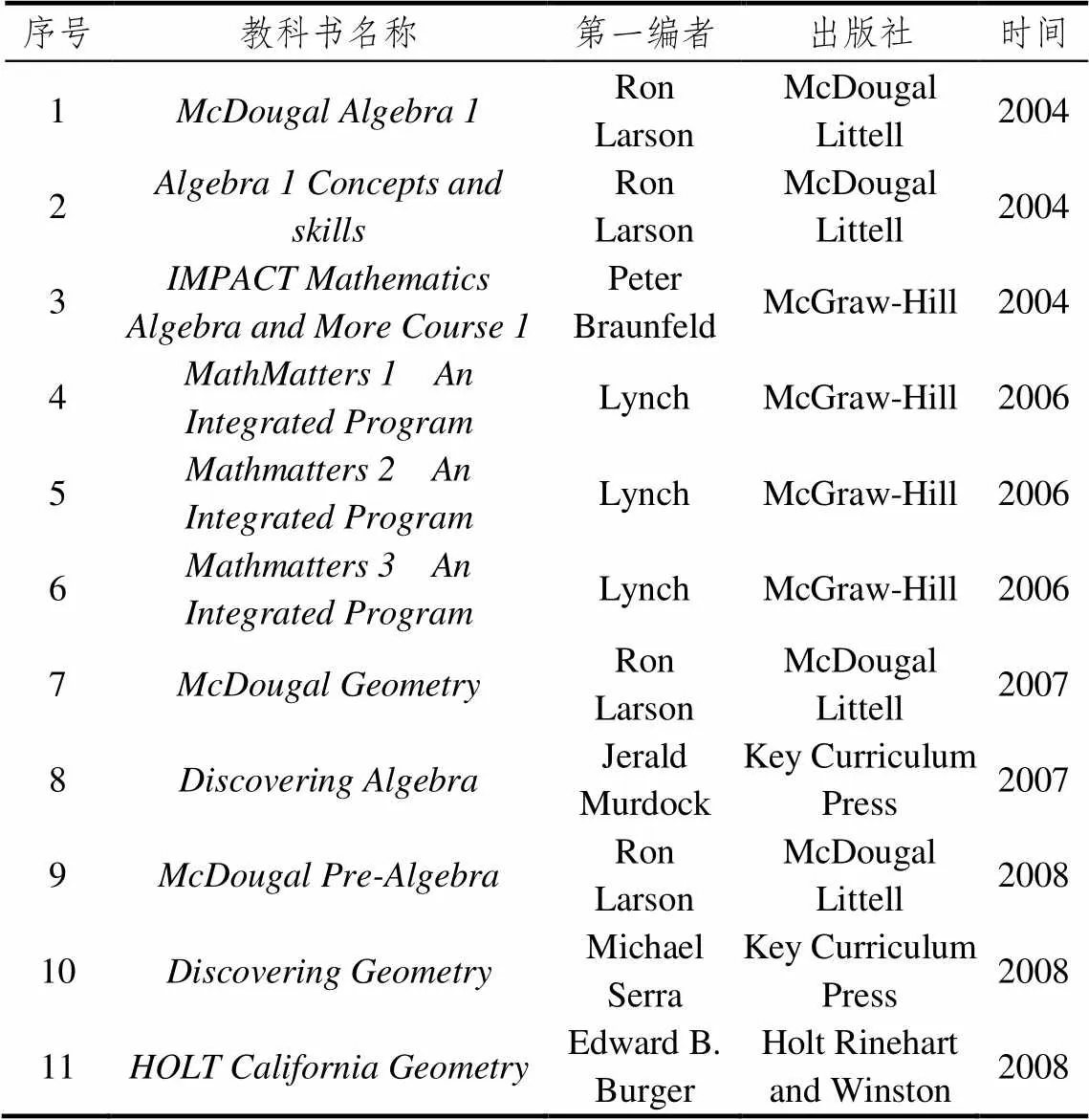
表1 编有中国数学史内容的11本美国初中数学教科书
研究者从栏目分布、内容分布和运用方式3个维度对这11本美国数学教科书中的中国数学史内容进行了梳理、比较和分析.研究如下问题:美国数学教科书中是如何呈现中国数学史内容的?具体包含了哪些中国数学史内容?又是如何运用这些内容的?对中国数学教科书编写数学史内容有何启示与借鉴?
2 教科书中的中国数学史栏目分布
美国初中数学教科书的栏目设置一般有:章头、引入、探究活动、例题、习题、旁白、阅读材料等.根据王建磐等人对教科书栏目的分类方法[5],将上述11本教科书栏目分为:非正文、引入、例题、习题4类,并统计其中的中国数学史内容,结果如表2所示.

表2 美国初中数学教科书中中国数学史栏目分布与数量
11本美国初中数学教科书中的中国数学史内容共25处,主要位于非正文、引入及习题部分,例题部分未查询到中国数学史内容,习题部分的中国数学史内容为9处,多为中国古代数学著作中的历史名题.其中,19处中国数学史内容以图文并茂的方式呈现,6处以文字叙述的方式呈现.
3 教科书中的中国数学史内容分布
基于数学史概念,将美国初中数学教科书中的中国数学史内容主要分为数学概念的起源与发展、历史名题、数学游戏3类,具体信息见表3.
3.1 数学概念的起源与发展
教科书,在“勾股定理”一节中提到,毕达哥拉斯定理是以生活在公元前6世纪的希腊数学家毕达哥拉斯的名字命名的.然而,这种关系在更早的时候就为人所知了,比如古巴比伦人、古埃及人和中国人.教科书在“勾股定理”一节中也提到,早在1000年左右,勾股定理就被中国人和古巴比伦人发明和使用.此书复习题第3题[6]介绍了中国最古老的数学和天文学的来源之一——《周髀算经》,并展示了著作中的赵爽弦图,让学生根据赵爽弦图来了解探究中国人是如何使用和证明的勾股定理,如图2.

表3 中国数学史内容分布
图2 利用赵爽弦图探究勾股定理
教科书,在“11.4勾股定理”一节的旁白处设置了历史链接[7](History Connection):“毕达哥拉斯定理最早的证明来自两千五百多年前的中国.你可以利用中国证明的图形来证明2+2=2吗?”(如图3)

图3 历史链接
教科书在“11.3勾股定理”一节的开头[8],介绍了中国古代数学著作《周髀算经》,并展示了与著作中类似的插图,图中包含4个全等的直角三角形和一个正方形(如图4).书中设置了3个问题,通过重新排列图形来比较非阴影区域的面积,以及探究非阴影区域与三角形边长的关系,从而引入勾股定理.

图4 介绍《周髀算经》与勾股定理
勾股定理作为初等几何中重要的定理之一,它从历史背景到多种证法都蕴含了丰富的数学史料,美版教科书不仅用文字叙述了勾股定理在中国的发展,还巧妙地设置问题情境,将赵爽弦图融入勾股定理的探究活动与问题之中,使数学史料更贴近学生的学习,拓宽学生的视野,寓数学教育于多元文化之中.《周髀算经》中赵爽弦图体现了中国古代数学的特色——面积“出入相补”原理,这种证明方法直观简明,也体现了数形结合的思想方法.
教科书在“5.4用矩阵求解方程组”练习题中的第15题提到:两千多年前,中国人发展了列方程矩阵作为求解线性方程的一种方法[7].对于线性方程组的研究,中国有着悠久的历史,《九章算术》的“方程章”主要讲述了一次方程组的解法.
教科书在“2.6分配律”一节的数学与历史[9](Math & History)模块展现了从古至今负数的发展与应用.首先介绍了负数的历史:“7世纪的印度数学家婆罗摩笈多(Brahmagupta,598—665)解释了负数的运算.直到16世纪,许多数学家仍然认为数值小于零的想法是荒谬的.早在公元前200年,中国就使用了负数.”接着提出问题:“从中国人提出负数概念到公元628年在印度被发现,大约相隔了多少年?”并用时间轴刻画了负数的发展历程,如图5.还绘制出西汉时期(负数最早出现于中国西汉时期编成的一部数学巨著《九章算术》的“方程章”中)数学家与皇帝讨论算筹的彩图,并标注:中国人用红色的算筹表示正数,用黑色的算筹表示负数.美版教科书中精心设计的彩图与文字相互映衬,使阅读材料“有滋有味”,能够吸引学生的阅读兴趣,拉近学生与数学史之间的距离.

图5 数学与历史模块
教科书在“1.1寻找模式”[10]一节中介绍帕斯卡三角形时,首先在新知引入中介绍:“早在公元1100年,中国和伊斯兰的数学家就开始研究三角形.1653年研究三角形的法国数学家布莱斯·帕斯卡(Blaise Pascal)称其为算术三角形,为了纪念帕斯卡,将它称为帕斯卡三角形.”并在旁白处展示了朱世杰《四元玉鉴》(《四元玉鉴》3卷,元朱世杰撰,成书于1303年,全书共24门,288问,是宋元时期最重要的数学著作之一,中国传统数学水平最高的著作,也是中国数学史和世界数学史上最早系统论述多元高次方程组解法的宝贵文献)卷首的第二幅图:古法七乘方圆图,配有文字介绍:帕斯卡三角形出现在中国数学家朱世杰于1303年写的《四元玉鉴》中(如图6).教科书在拓展资料[7]“帕斯卡三角形”也设置了古法七乘方圆图(如图7),图片下方介绍:“帕斯卡三角形其实是朱世杰于1303年在《四元玉鉴》上首次发表的.”图7中的插图来自《四元玉鉴》卷首的第二幅图[11]:古法七乘方圆(如图8).但教科书在引入史料时,未核实史料的正确与否,误用“首次”一词,认为帕斯卡三角形是由朱世杰首次提出的.其实,朱世杰在《四元玉鉴》中发表的“古法七乘方圆图”是北宋贾宪“开方作法本源图”(即贾宪三角,贾宪三角是开方作法本源图的今称,由中国北宋数学家贾宪所创.西方的帕斯卡三角形的提出,晚于贾宪三角600年.贾宪三角是一个指数为正整数的二项式定理系数表)的推广,由七层推广到九层(八次幂),又用线条将各个数字连结起来,进一步展示出这些数字之间的规律:除三角形两条斜边都是由数字1所组成,其它的数字都等于它肩上的两个数之和.此图在杨辉《详解九章算法》“少广”章中有记载,指明此图:“出释锁算书,贾宪用此术.”[12]可知贾宪才是这三角形的发明人.

图6 介绍《四元玉鉴》

图7 拓展资料中的古法七乘方圆图

图8 古法七乘方圆
美版教科书在讲述帕斯卡三角形的时候,不忘追根溯源,引入数学家朱世杰的《四元玉鉴》,此书的数学成就已得到国际科技史界的瞩目和公认,美国科技史家萨顿称《四元玉鉴》是“中国数学著作中最重要的一部,同时也是整个中世纪最杰出的数学著作之一”,并称朱世杰“是他所生存时代的、同时也是贯穿古今的一位最杰出的数学家”[13].
3.2 历史名题
数学历史名题体现和谐之美,是人类文化的瑰宝,中国古代数学著作中蕴含了丰富的数学名题,以实际应用为目的,与生活紧密相连,颇有趣味.
教科书在“2.6用乘法或除法解方程”一节的习题39[14]将《九章算术》中的一道问题进行变式,题为:“一只羊、一匹马和一头牛误入农夫的麦田,吃了一些禾苗.马吃的是羊的两倍,牛吃的是马的两倍.农夫要求牲畜的主人给他5斗小麦来代替它们吃的东西.羊的主人应该给多少小麦?马的主人呢?牛的主人呢?”紧接着题目下方给出点拨.
a. 设为羊的主人应该给的小麦量(单位为斗).怎样用表示马的主人应给的数量?牛的主人呢?
b. 列一个方程并解出.到十分之一斗,每个牲畜的主人需要给多少小麦?
此题选自《九章算术》第三卷“衰分”,原题为[15]:今有牛、马、羊食人苗.苗主责之粟五斗.羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?该题考查的是按比例分配,美版教科书巧设未知数,列方程来解答此题,但未交代该题出自中国的《九章算术》.
教科书在“第9章勾股定理”中的习题22[6],引用了《九章算术》勾股章的习题.书中首先介绍了《九章算术》是中国古代数学教材,共有246道习题,许多题目使用了勾股定理,即毕达哥拉斯定理的中文名称,指出勾股定理为:勾2+股2=弦2.接着叙述了此题:“一根绳子从一木柱的顶端垂下来,有三尺在地上.当把绳子拉紧,使它的一端刚好接触到地面时,它离木柱的底部有八尺远.绳子有多长?”题旁插入了绳子与木柱的图片,形象地描绘了题目,将题意用图画(如图9)的方式呈现出来,易于学生的理解.图旁还使用中文标注着《详解九章算术》中的解法:木长如股索,余如股弦较;木长如股弦,索斜之如弦.原题为:“今有立木,系索其末,委地三尺.八尺而索尽.问:索长几何?”美版教科书直接引用中国的历史名题,插入带有中国汉字的插图,为学生提供了不同文化背景下的题目.

图9 引用《九章算术》勾股章中的习题
《九章算术》是中国传统数学中最重要的经典著作,历来被尊为算经之首.它之于中国和东方数学,大体相当于《几何原本》之于希腊和欧洲数学.在世界古代数学史上,《九章算术》和《几何原本》像两颗璀璨的明珠,东西辉映[16].《九章算术》集先秦到西汉的数学知识之大成,全书包含246个题目,题目由“问”“答”“术”3部分组成.它具有理论密切联系实际的风格,以计算为中心,奠定了中国传统数学的基本框架,不仅使数学成为中国古代最为发达的基础科学学科之一,而且深刻影响了此后两千余年间中国和东方的数学发展.《九章算术》具有如此重要的地位,这大概也是美国数学教科书融入其中名题的主要原因.
教科书在第2章“比例推理与变异”复习题的Improving your reasoning skills(提高你的推理能力)版块中有一道题目[7]:“一位城市官员在监测用水情况时,看到一位妇女在河里洗盘子.他问:‘这里为什么这么多盘子?’她回答道:‘这所房子里有一个晚宴.’他又问:‘有多少客人出席聚会?’女人不知道但回答道:‘每两位客人共用一盘米饭,每3位客人吃一道菜肉汤,每四位客人用一个盘子吃肉,宴会上总共用了65个盘子.’有多少客人参加了晚会?”此题是著名的“河上荡杯”问题(荡杯,即洗碗),教科书中介绍此题来自于中国古代著作《九章算术》,这是错误的,此题首先出自成书于公元400年前后的《孙子算经》中的第17题,《张邱建算经》和吴敬的《九章算法比类大全》中也存在这一题.而美国教科书误认为此题来自《九章算术》,可能是与《九章算法比类大全》混肴了.
原题是:今有妇人河上荡桮(杯的繁体字).津吏问:“桮何以多?”妇人曰:“家有客.”津吏曰:“客几何?”妇人曰:“二人共饭,三人共羹,四人共肉,凡用桮六十五,不知客几何?”此题故意将解法的思想过程隐藏起来,使读者很难领会解决同类问题的一般原则,从而锻炼学生的推理能力.题旁还展示了一幅来自17世纪中国的卷轴画《四季风景》(如图10).除了“河上荡杯”问题,“鸡兔同笼”“物不知数”等名题也都出自《孙子算经》.

图10 “河上荡杯”问题
教科书在“17.3用线性组合求解线性系统”一节的数学与历史模块[9]介绍了线性方程组的历史(如图11).从古至今,首先介绍了第一个线性方程组来自中国1247年的《数书九章》(该书内容异常丰富,计分大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易等9大类),给出书影及书中第八章军旅类中的“计造军衣”习题,原题是:“问库有布绵絮三色,计料欲制军衣.其布,六人八匹,少一百六十匹,七人九匹,剩五百六十匹.其绵,八人一百五十两,剩一万六千五百两,九人一百七十两,剩一万四千四百两.其絮,四人一十三斤,少六千八百四斤,五人一十四斤,适足.欲知军士及布绵絮各几何?”[17]接着用精美的图片和简略的文字回顾了从公元前3000年的第一个算盘,发展到1879年的收银机以及今天的带有扫描仪的收银机,展示了数学带来的科技进步.除这本教科书外,教科书,在“7.3用线性组合解线性系统”一节中也引入了此问题.

图11 介绍线性方程组的历史
图12是教科书“第2章比例推理与变异”的一道复习题[7],摘自《数书九章》第十二卷凡六问中“米谷粒分”问题,原文是:“问开仓受纳,有甲户米一千五百三十四石到廊,验得米内夹谷.乃于样内取米一捻,数计二百五十四粒,内有谷二十八颗.凡粒米率,每勺三百,今欲知米内杂谷多少,以折米数科责及粒,各几何?”[17]中国2015年湖北高考数学选择题也出过此题:粮仓开仓收粮,有人送来米1 534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为多少?

图12 “米谷粒分”问题
《数书九章》由南宋数学家秦九韶1247年编著完成,此书综合了前此的算学精华,并发挥了他的高度创造性,记载了秦氏的创造和发明,多誉之为算中宝典,是祖国至可宝贵的数学遗产.美国著名科学史家萨顿就曾指出:秦九韶是“他那个民族、他那个时代,并且确实也是所有时代伟大的数学家之一”[17].
中国古代数学体现出算法化的优秀数学思想,数学历史名题是在数学的发展,生产生活中产生的,具有相应的历史事实背景,能够体现数学思想方法.教科书中融入历史名题,能够直接反映当时的社会生活状况,也能了解当时人们的数学思维水平[18].解答数学历史名题,有助于培养学生的数学文化,也能使枯燥乏味的习题教学变得丰富多彩,见识到不同国家不同民族的文化生活,激发学生的学习兴趣.
3.3 数学游戏
七巧板是中国民间流传的一种拼图游戏,起源于宋代,后来传到欧、美、日本等许多国家和地区,又叫做“七巧图”“唐图”“智慧板”“流行的中国拼板游戏”“中国解谜”“东方魔板”等[19].搜集到的教科书中,有7本美国初中数学教科书涉及了中国七巧板的内容,具体信息见表4.

表4 美国初中数学教科书中的七巧板具体内容
由表4可知,中国七巧板多被应用于美国初中数学教科书的平面几何部分,如多边形对角线数目的探究、梯形概念的学习、正方形面积的推导、勾股定理的探究以及七巧板习题的变式等.美版教科书给予学生充分发挥想象力和创造力的空间,巧妙地利用了七巧板的灵活性、随意性和可操作性,学生直接利用七巧板或在纸上裁剪出各个板块,亲手制作七巧板,将其任意排列拼成不同形状的图形,在享受无穷乐趣的同时又经历新知识的探究过程,增长学习经验,提高几何直观能力.
研究七巧板的专家们一致认为,七巧板源于中国古时的勾股法,1846年出版的《七巧图集成》中有这样的话:“以七尖方,运勾股法,不觉三才万象,悠然而毕会千心,灿然而具列千目,非天下之至巧,其孰能与千此.”稍后于1861年出版的《七巧八分图》更直截了当地说:“七巧图传世久矣,源出勾股,意蕴精深,端倪层出不穷.”[20]既然七巧板源于勾股,显然勾股定理的探究中少不了七巧板,能让学生在拼图游戏中探究定理,何乐而不为?
4 教科书中运用中国数学史的方式
依据数学史与数学知识的关联程度,华东师范大学汪晓勤教授将数学教科书运用数学史的方式分为5种类型:点缀式、附加式、复制式、顺应式、重构式,具体信息如表5所示[21].

表5 数学教科书运用数学史的5种方式
由表5及美版教科书中的中国数学史内容分布的统计,发现美版教科书中的中国数学史运用方式多为直接引入,运用点缀式融入数学史料有2处,运用附加式有10处,运用复制式有4处,运用顺应式有9处,如图13.

图13 美国初中数学教科书中的中国数学史的运用方式
(1)点缀式.
点缀式运用中国数学史料主要出现于正文中,为知识点、习题等补充背景图片.如美版教科书中引入《数书九章》中的一道题目,在题旁插入了《数书九章》的书影以及古算盘的图片.点缀式史料主要是反映相关主题的历史图片,起到装饰的作用.
(2)附加式.
附加式运用中国数学史料主要出现于引入、阅读材料、正文叙述内容中.如先介绍七巧板的历史,起源于中国,由5个等腰直角三角形、一个正方形和一个平行四边形组成,后设置以七巧板为背景素材的习题,或引出三角形和四边形面积公式的推导等探究活动.教科书在呈现帕斯卡三角形内容介绍了朱世杰《四元玉鉴》中的古法七乘方圆图.教科书“矩阵与行列式”一节的“Math: Who, Where, When”栏目中介绍了类似与行列式的分离系数方法可以追溯到12世纪的中国数学家,中国人研究解决方程组的模式时,发现了可以将数值系数排列成一个方阵,类似于计算器(算盘)上的方阵.教科书设置数学与历史模块,介绍了负数的发展历史.附加式数学史料为教科书相关知识点介绍了历史背景,补充了历史知识,篇幅简洁明了,个别教科书还设置了精美的插图,形象生动,将数学史料跃然纸上,让学生身临其境地经历数学概念的发展过程.
(3)复制式.
复制式运用中国数学史料主要出现于习题中,多为直接呈现中国数学历史名题.如直接引入《九章算术》勾股章的绳子问题、“河上荡杯”问题、《数书九章》中的“计造军衣”与“米谷粒分”等问题.美版教科书展现了中国古代优秀的数学文化和思想方法,丰富了历史名题的现实意义,让学生感受不同文化背景下的优秀文化.
(4)顺应式.
顺应式运用中国数学史料主要出现于引入、探究活动、拓展题等部分.如教科书在“对角线和多边形的角”一节中利用中国古代的七巧板,引导学生将任何数量的板块排列组合成不同的图形,进而确定不同多边形对角线的数目.教科书在“勾股定理”一节中引入了中国古代数学著作《周髀算经》中的插图,通过4个直角三角形和正方形的组合来探究勾股定理.教科书在“勾股定理”一节中利用七巧板探究勾股定理(如图14).首先,让学生在坐标纸上画出七巧板的简图,并用给定的字母标记每一块,将这7块剪下来;其次,在另一张纸上画出七巧板中的一个大三角形,并用所有的七巧板在大三角形的直角边处,以两直角边为边长组成两个正方形;最后,将所有的七巧板沿着大三角形的斜边组成一个正方形.通过此过程引导学生观察拼成的正方形和三角形,探求它们之间的边长和面积关系,得到勾股定理.教科书,在“比例与测量系统”的章后拓展题中以七巧板为背景,设置了一道习题,求每个七巧板的面积与整个正方形的面积之比.顺应式运用中国数学史料以中国数学历史为背景,再现古人思想,设置题目与探究活动,起到古为今用,推陈出新,激发学生学习兴趣的作用.

图14 七巧板
5 结论与启示
5.1 结论
通过对11本美国初中数学教科书中的中国数学史内容的设置分析,得出以下结论.
(1)美国初中数学教科书中的中国数学史主要设置于非正文、引入和习题部分,多以图文并茂的形式呈现,不仅叙述了中国数学史料,而且设置了精美的插图,将史料以图画的形式展示出来,形象生动地与教科书所融合.
(2)美国初中数学教科书中的中国数学史内容展示了中国优秀的传统文化.书中以多样的形式呈现了勾股定理内容涉及的中国数学史料,包括文字叙述勾股定理在中国的历史、赵爽弦图的变式应用、《九章算术》中的历史名题、《周髀算经》中的证明方法等;精美的阅读材料版块,从古至今展示了负数以及线性方程组的历史;古著作中的原图跨越国界,呈现了朱世杰著作中的“帕斯卡三角形”.中国古代数学著作中的历史名题被应用到习题部分,展示了中国优秀的古代数学思想,如面积“出入相补”原理,将中国古代数学代数化、算法化等与西方公理化相结合.中国发明的七巧板在美版教科书中的平面几何部分灵活应用,尽显奥秘.遗憾的是,部分数学史料的引入出现了错误,如误认为“帕斯卡三角形”最早是由朱世杰发现的,河上荡杯问题的出处出现了错误.
(3)美国初中数学教科书以点缀式、附加式、复制式和顺应式为主,将中国历史名题、七巧板、古著作等优秀文化融入教科书中,为知识补充历史材料,为题目增添历史气息,为活动创设人文乐趣,重构式间接引入数学史略显不足.
5.2 启示
美国初中数学教科书的中国数学史内容的融入对中国数学教科书的编写有如下启示.
(1)坚持“立德树人”,坚定对中华优秀传统文化的自信.美国教科书中展示了勾股定理、负数、线性方程组等内容在中国的历史渊源,融入中国古代数学著作中的历史名题,以多种形式学习中国优秀的传统文化.文化是一个国家、一个民族的灵魂.中华优秀传统文化是中华民族的独特标识和突出优势,中国数学教科书中在融入外国数学史的同时,理应大力弘扬中国优秀的数学史内容,不忘初心,让优秀传统文化进课本、入课堂,在潜移默化中渗透数学文化,拓宽学生的视野,使中华文明得以传承.
(2)数学教科书的编写应追根溯源,求真求实,注意数学史运用的正确性.在呈现某一数学知识的历史背景时,要尊重历史,“刨根问底”,展现历史的本来面目,将历史背景了解得十分透彻全面,再融入教科书中,尤其对“首次”要核实清楚,以免发生错误.中国北师大版七年级下册“完全平方公式”一节的“读一读”中介绍了杨辉三角,并给出贾宪的“开方作法本源图”以及欧洲的帕斯卡三角形;华师大版八年级上册“乘法公式”一节最后的阅读材料中介绍了贾宪三角;人教版八年级上册“完全平方公式”一节的阅读与思考中也介绍了杨辉三角,但文中仅提到贾宪也用过此方法,并没有提到贾宪才是发明人,这一点可能会让学生对此三角形的真正发明人产生误解.
(3)数学教科书的编写应名题变式,以题说法.将古代经典数学著作中的名题适当融入中小学数学教科书中,将现代数学和古代经典数学连接起来,有助于学生了解历史文化、多元文化背景下进行数学思考,学习逻辑分析方法.中国北师大版八年级上册将《孙子算经》中的鸡兔同笼问题单独设一节,将古算题带进学生的学习生活.名题的引入也要注意方式,既可采取复制式直接引入,或者将其变式成符合当今时代背景的习题,拉近学生与名题之间的距离,利用名题讲解一些古代具有影响力的数学思想方法,开拓学生的视野.也可将数学史料以问题的形式融入教学过程中,寓史料于问题链中,潜移默化地向学生渗透数学史.
(4)数学教科书的编写可以适当游戏数学,玩中传知.美版教科书多次应用中国古代玩具七巧板,仅凭7个规则的板块,就给游戏者以充分发挥想象力和创造力的空间,在组合板块的同时,锻炼学生的空间想象能力和逻辑思维能力,在享受无穷乐趣的同时锻炼了智力.中国古典智力游戏3绝:七巧板、九连环和华容道.它们的背后有着许多有趣的数学问题,不管是在教科书的编写还是教学过程中,可以适当融入数学游戏,玩中学,做中学,体验过程,获取新知.
(5)数学教科书的编写应图文并茂,设计精美.中国数学教科书中一般设置单独的版块引入数学史料.例如:人教版“有理数的加减法”一节中设置“阅读与思考”,介绍了中国人最先使用负数,还插入古代红色与黑色的算筹表示数的图片;北师大版“有理数”一节的读一读设置了“负数小史”,以文字形式叙述了负数的历史;华师大版“有理数的加减混合运算”一节中的阅读材料介绍了中国人最早使用负数以及《九章算术》的历史和中国古代的“正负术”,也是以文字形式进行叙述的.中国数学教科书以文字形式对史料进行介绍,与美版教科书利用图文并茂的形式相比少了点趣味和吸引力,缺乏艺术性与美感.为增强学生的阅读兴趣,将拓展史料与正文相区别,应适当在版面设计时加以修饰,将某一知识点背后的数学史设计成精美图片或卡通图等样式,尽量减少纯文字的罗列,将数学史融入教学情境或教科书情境中.
[1] 汪晓勤,韩祥临.中学数学中的数学史[M].北京:科学出版社,2002:2.
[2] 汪晓勤.古为今用:美国学者眼中数学史的教育价值[J].自然辩证法研究,2004,20(6):73-77.
[3] 余介石.数之意义[M].上海:商务印书馆,1945:1-10.
[4] 全美数学教师理事会.美国学校数学教育的原则和标准[M].北京:人民教育出版社,2004:1.
[5] 王建磐,汪晓勤,洪燕君.中、法、美高中数学教科书中的数学文化比较研究[J].教育发展研究,2015,35(20):28-32.
[6] SERRA M. Discovering geometry [M]. Berkeley: Key Curriculum Press, 2008: 508, 531.
[7] MURDOCK J. Discovering algebra [M]. Berkeley: Key Curriculum Press, 2007: 159, 161, 184, 620.
[8] LYNCH. Mathmatters 2 an Integrated program [M]. Seattle: McGraw-Hill, 2006: 503.
[9] LARSON R. McDougal algebra 1 [M]. EVANSTON: McDougal Littell, 2004: 128, 438.
[10] BRAUNFELD P. IMPACT mathematics algebra and more course 1 [M]. Seattle: McGraw-Hill, 2004: 16.
[11] 朱世杰.四元玉鉴[M].郭书春,译.沈阳:辽宁出版社,2006:1.
[12] 沈康身.历史数学命题赏析[M].上海:上海教育出版社,2010:1 042.
[13] 周瀚光.科学史与科技古籍研究[M].上海:上海社会科学院出版社,2017:324.
[14] LARSON R. McDougal Geometry [M]. EVANSTON: McDougal Littell, 2007: 1.
[15] 九章算术[M].郭书春,译.沈阳:辽宁教育出版社,1998:249.
[16] 郭书春.中国古代数学[M].北京:商务印书馆,1997:6.
[17] 王守义.数书九章新释[M].北京:商务印书馆,1992:1.
[18] 张维忠.数学史融入初中数学教育研究[M].贵阳:贵州大学出版社,2017:155.
[19] 张祥斌.聪明人最爱的逻辑游戏500个[M].北京:中国财富出版社,2014:1.
[20] 吴鹤龄.七巧板、九连环、华容道:中国古典智力游戏三绝[M].北京:科学出版社,2015:71.
[21] 汪晓勤.法国初中数学教材中的数学史[J].数学通报,2012,51(3):16-20,23.
[22] 姜浩哲,汪晓勤.美国《线性代数及其应用》教材中的数学文化研究[J].高等理科教育,2019(3):74-80.
[23] 邵爱娣,栗小妮,汪晓勤.美国早期代数教科书中的“负负得正”解释方式研究[J].数学教育学报,2021,30(1):85-90.
[24] RON LARSON. Algebra 1 Concepts and skills [M]. EVANSTON: McDougal Littell, 2004: 210.
[25] LYNCH. Mathmatters 1 An Integrated Program [M]. Seattle: McGraw-Hill, 2006: 188.
[26] LYNCH. Mathmatters 3 An Integrated Program [M]. Seattle: McGraw-Hill, 2006: 126.
[27] RON LARSON. McDougal Pre-Algebra [M]. EVANSTON: McDougal Littell, 2008: 147.
[28] EDWARD B. HOLT California Geometry [M].ARIZONA: Holt Rinehart and Winston, 2008: 158.
[29] 姜天卓,李淑文,秦德生.学生使用数学教科书的国际研究现状与趋势——基于WOS数据库的HistCite计量分析[J].数学教育学报,2023,32(1):66-72.
[30] 张英伯.数学文化盛宴——评代钦著《艺术中的数学文化史》[J].数学教育学报,2023,32(1):99-101.
[31] 姜浩哲,沈中宇,邹佳晨.中美基础教育数学课程发展:比较与启示——蔡金法教授访谈录[J].数学教育学报,2023,32(3):56-63.
[32] 王玉,胡凤娟.中英高考数学概率与统计部分的比较研究[J].数学教育学报,2023,32(3):24-29.
[33] 温建红.基于数学核心素养培养学生提出问题能力的意义与策略[J].数学教育学报,2023,32(3):13-17.
History of Chinese Mathematics in American Middle School Mathematics Textbook
WANG Bin1, 2, LI Chun-lan1, ZHANG Tao3
(1. School of Mathematical Science, Inner Mongolia Normal University, Inner Mongolia Hohhot 010022, China;2. Xinhui Middle School, Inner Mongolia Chifeng 024399, China;3. Institute of History of Science and Technology, Inner Mongolia Normal University, Inner Mongolia Hohhot 010022, China)
On the basis of studying and analyzing 11 American junior middle school mathematics textbooks in the early 21st century, this paper sorts out the contents of Chinese mathematics history integrated into these textbooks from three aspects: column distribution, content distribution and application mode. It is found that many American junior middle schools’ math textbooks introduce Chinese math history content in exquisite and unique layouts, such as the Pythagorean theorem, negative numbers, linear equations, famous questions in ancient Chinese math works and tangram and so on. Regarding the integration of Chinese mathematics history into American junior middle school mathematics textbooks, we get five enlightenments: strengthen confidence in the excellent traditional Chinese culture; trace back to the source and seek truth and reality; change of title and use questions to teach the method; learn math in games; illustrated and beautifully designed, and, it’s fun and artistic.
history of Chinese mathematics; America; middle school mathematics textbook; famous question of mathematics history; tangram; a sense of national pride; cultural self-confidence
G423.3
A
1004–9894(2024)01–0077–08
王彬,李春兰,张涛.美国初中数学教科书中的中国数学史[J].数学教育学报,2024,33(1):77-84.
2023–09–12
内蒙古自治区哲学社会科学规划项目——落实中小学数学教科书立德树人任务研究(2021NDB197);内蒙古自治区高等学校科学研究项目(教育厅人文社科重点项目)——中国数学科普读物整理与研究(1912—1952 年)(NJSZ21004);内蒙古自治区研究生教育创新计划资助项目,内蒙古师范大学研究生科研创新基金资助项目——国外数学教科书中的中国数学史设置之研究——以美国初中数学教科书为例(CXJJS20087)
王彬(1997—),女,内蒙古赤峰人,硕士生,主要从事数学史与数学教育研究.李春兰为本文通讯作者.
[责任编校:陈汉君、陈隽]

