高考地理表格数据题的隐性信息处理*
奉明茂 邓 喆
(湖南省郴州市第三中学,湖南 郴州 423000)
统计方法在地理学中的应用十分广泛,其中表格数据统计是常用的方法。利用表格数据分析地理事物的特征、分布,并推测其成因,以此考查学生综合认识地理事物和现象和分析地理要素相互作用关系的能力,这是近年来高考试题中的常见考查形式。掌握正确的数据分析方法,形成良好的数据处理思路,找出其隐含的信息,就能快速解答这类试题。
一、找数据规律,析影响因素
表格数据题所呈现的数据大多是有规律可循的,一般有以下规律:数据平稳变化、数据递变、数据突变、数据波动等。解题时从表格数据中快速找出这些规律,就能化复杂为简单,从而找到答题的方向。
【例1】(2021年湖南省高考)某市地铁S线和T线开通前后距地铁线不同距离的住宅平均价格及其增幅如表1所示。S线横跨城市中心区和边区,T线连接城市边区和外围区,两条线路开通时间几乎相同,所经之地公共交通密度差异明显。据此完成下面小题。

表1 某市地铁S线和T线开通前后距地铁线不同距离的住宅平均价格及其增幅
1.地铁开通后,S线和T线距地铁线0.2千米范围内住宅平均价格相对较低的主要原因是
A.治安环境较差 B.运营期间交通较拥堵
C.大气质量较差 D.运营期间噪音和震动感较大
2.仅从距地铁线远近对住宅价格影响角度看,S线和T线开通后对住宅平均价格有效影响的距离分别不超过
A.2.5千米、1千米 B.1千米、1千米
C.3千米、3千米 D.2.5千米、3千米
本组试题数据量较大,许多学生初看此题,会被庞大的数据信息迷惑,感觉到无从下手。其实只要找出S线和T线开通后六年内距地铁由近及远的平均房价递变规律,如图1所示,试题就变得清晰了。表中S线开通后六年的平均房价数据自上而下依次为:①13160.0,②28900.0,③25493.7,④23383.3,⑤18760.6,⑥17066.7,⑦12941.6,⑧10008.3,⑨12115.0。
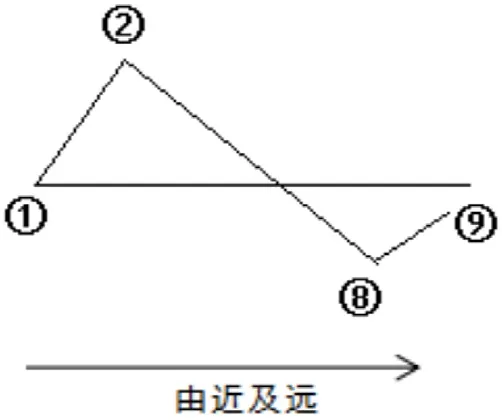
图1 平均房价递变规律
从这些数据的排列来看,其递变规律是:①~②上升,②~⑧下降,⑧~⑨上升(T线递变规律判断方法相同)。总结出这个递变规律后,问题就变得较为清晰。
第1题,距地铁最近的①处(0.2千米内)房价较低,这是地铁带来的不利影响,跟地铁相关的不利影响显然是地铁产生的噪声震动大,故选D。
第2题,要求判断S线和T线开通后对房价的有效影响距离。离地铁近则交通相对便利,房价自然较高,受地铁距离的影响,房价会逐渐降低。从S线房价示意图来看,在②~⑧阶段,房价一路走低,到⑧处之后,房价又开始上升,说明②~⑧段的价格是受地铁距离影响的。⑧处是转折点,⑧对应的房价是10008.3元每平方米,对应的地铁距离是2.5千米(同理,T线对应的距离则1千米),故选A。
在解答这类试题时,先要理清思路,观察数据排列中是否有规律可循,总结规律后再从不同角度分析影响数据变化的原因,问题就会变得简单。
二、看数据极值,探形成原因
数据极值包括数值最大值和最小值,是地理事物在特定环境下产生的数据,常常成为命题的切入点。利用特殊数据考查学生对地理事物发生发展的理解是常见的考查方向。
【例2】冰川物质平衡线是冰川积累区与消融区的界线。某团队运用模型计算青藏高原不同山地发育冰川的临界海拔,得出结果如表2所示。据此完成下面小题。
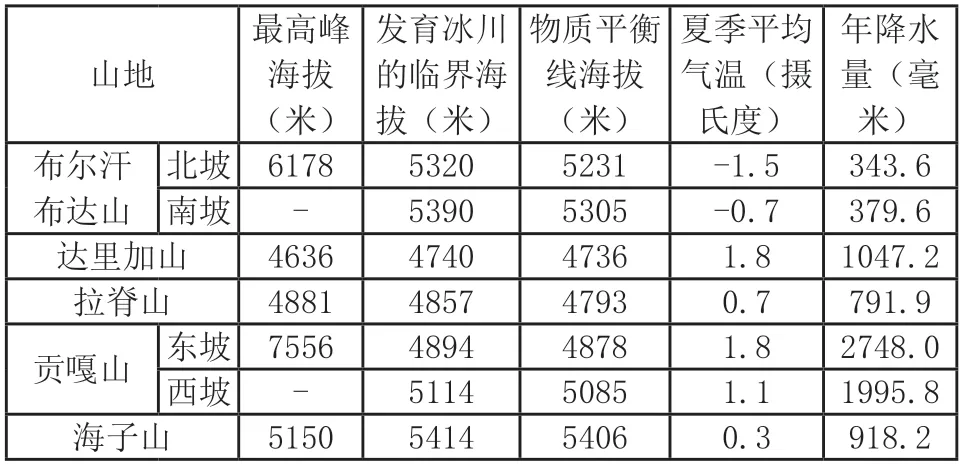
表2 青藏高原不同山地发育冰川的临界海拔
1.根据表格信息可以推测出贡嘎山
A.接近青藏高原腹地 B.受寒潮影响较大
C.纬度位置最高 D.受夏季风影响显著
2.与其他山地相比,布尔汗布达山发育冰川的临界海拔远高于物质平衡线,主要是因为该山
A.海拔较高 B.降水较少
C.气温较高 D.物质平衡线较高
本组试题提供的几座山学生都比较陌生,这就要求学生对情境材料中的数据进行快速处理,因为表中不同的山体数据没有递变规律,所以只能找极值。表中的极值有:①布尔汗布达山北坡夏季气温最低,年降水量最少;②达里加山最高峰海拔最低,发育冰川的临界海拔最低;③贡嘎山东坡海拔最高,同时也是所有山脉中降水最多的。找出极值后可以从影响极值的条件进行分析,快速找出问题的答案。例如,第1题是推测贡嘎山的自然环境特征,通过前面极值的分析可知贡嘎山东坡降水最多,与这个极值相关的答案显然是D(与东南季风有关)。贡嘎山降水多不可能接近青藏高原腹地,故A选项错误;青藏高原受寒潮影响小,故B选项错;表中所有山脉都位于青藏高原,纬度位置大体相当,贡嘎山降水多,不能由此推测其纬度位置,故C选项错。
第2题的解答也一样,布尔汗布达山在表中数据有两个极值:①布尔汗布达山北坡夏季气温最低;②年降水量最少。冰川临界海拔高于物质平衡线,其原因要么是气温不够低,不利于冰川的发育,要么是降水量不够,导致冰川发育少。从找出的两个极值看,布尔汗布达山北坡夏季气温最低,所以不是这个原因导致的。而第二个极值是布尔汗布达山北坡年降水量最少,这显然与题干所问相符,故B项正确。C选项“气温较高”属于直接信息解读错误,表中该山北坡气温是最低的;D选项也是属于常识表述错误,题干中问的是“布尔汗布达山发育冰川的临界海拔远高于物质平衡线”的原因,这与物质平衡线本身高低无关。
这类试题利用数据极值设计问题,在解题时,要善于从表格中快速找到极值,从而找到问题的切入口。
三、洞数据联系,比数值大小
很多数据不是孤立存在的,一些数值的大小与其他数据有着密切联系,有些数值间甚至会有严谨的运算关系,很多隐性数据就隐藏在这种数值关系之中。
【例3】2022年中央一号文件强调“挖掘农业碳汇潜力,推进农业纳入全国碳市场”。农业生产中的碳排放主要来自化肥、地膜等农资使用和能源消耗、畜牧养殖和秸秆燃烧等环节;碳汇主要来自植物光合作用、秸秆还田等植物和土壤固碳。黄土高原区不同农业生产模式碳效应对比数据如表3所示。据此完成下面小题。
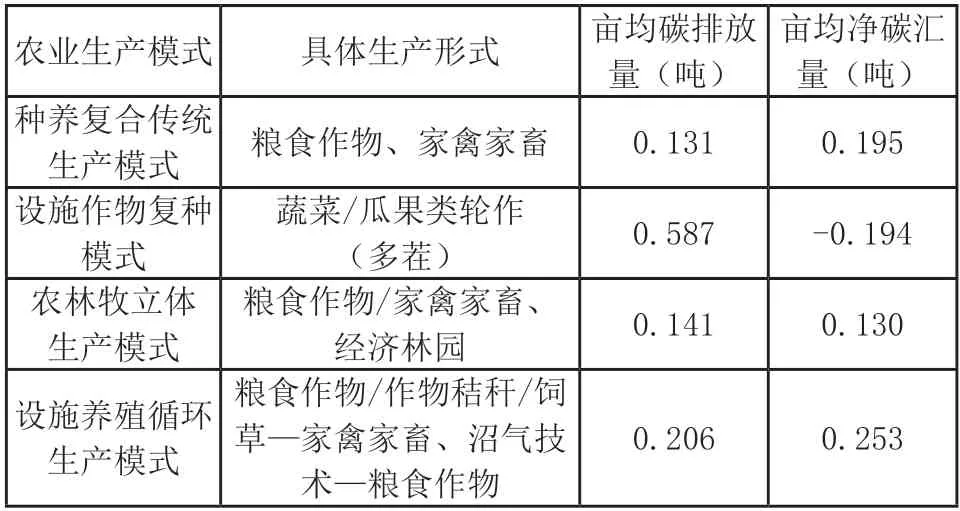
表3 黄土高原区不同农业生产模式碳效应对比数据
说明:净碳汇量常用碳汇量与碳排放量之间的差值来衡量。
1.关于不同农业生产模式碳汇量的描述及原因,说法正确的是
A.种养复合传统生产模式:碳汇量最大,粮食作物秸秆还田量大
B.设施作物复种模式:碳汇量最小,蔬菜光合作用弱
C.农林牧立体生产模式:碳汇量最小,土壤固碳少
D.设施养殖循环生产模式:碳汇量最大,秸秆还田和土壤固碳量大
2.从发展低碳农业的角度,黄土高原区退耕还林农户适宜发展的生产模式是
A.种养复合传统生产模式 B.设施作物复种模式
C.农林牧立体生产模式 D.设施养殖循环生产模式
在解答这组试题时,必须弄清楚碳汇量、净碳汇量、碳排放量三者之间的关系,建立它们之间的数据计算公式,这样才能把隐藏的数据挖掘出来。根据文字材料“净碳汇量常用碳汇量碳排放量之间的差值来衡量”,可以得出如下数据关系:净碳汇量等于碳汇量减碳排放量。因此,只要知道其中两个变量,就能计算出第三个变量的数值。例如,第1题要求比较不同农业生产模式的碳汇量的大小,根据数据关系可得:碳汇量等于净碳汇量加碳排放量。由此可计算得出:种养复合传统生产模式其亩均碳汇量为0.326吨,同理设施作物复种模式为0.393,农林牧立体生产模式为0.271,设施养殖循环生产模式为0.459,农林牧立体生产模式碳汇量最小是因为秸秆还田少,D正确。利用数据之间的关系判断第2题,表中数据设施养殖循环生产模式的净碳汇量最多,符合发展低碳农业,故第2题应选D。
由此可见,当不同数据间有关联时,要善于找出数据间的关系以简化问题。
四、看数据时间,联时代特征
地理事物在不同的发展阶段具有不同的特征,有些数据如果不与时代特征相联系,就很难判断数据所反映的地理事物的发展特征。在解题时一定要从时代背景入手,宏观把握地理事物发展进程,做到因时而异,才能真正理解数据所体现的地理事物的特征。
【例4】城市用地增长弹性系数是城市建成区面积和城市人口增长率的比值,通常被用来衡量城市用地扩张与人口间的协调关系,一般认为该系数为1.12时比较合理。我国各时期的城市用地增长弹性系数如表4所示。据此完成下题。
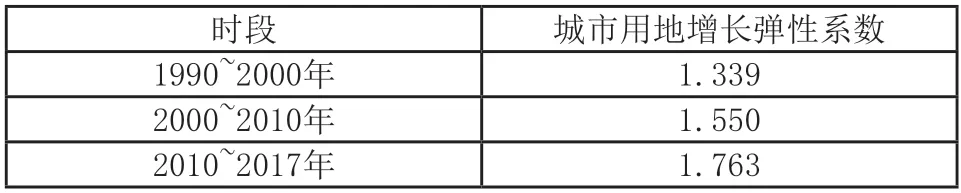
表4 我国各时期的城市用地增长弹性系数
1.城市用地增长弹性系数不断扩大的原因可能是
A.人口城镇化增速变缓 B.城镇人口峰期较晚
C.二者的快速增长期不同 D.城市用地峰期较早
如果不从时间角度思考我国城市发展速度和人口增长状况,很容易得出错误的结论。根据材料提供的信息,可以得出:城市用地增长弹性系数等于城市建成区面积除以城市人口增长率。由以上数据关系可以得出城市用地弹性系数增大有下列三种情况:①城市建成区面积扩大时,城市人口增长率下降;②城市建成区面积缩小时,城市人口增长率下降得更快;③城市建成区面积扩大较快,而城市人口增长率增长速度较慢。表中城市弹性系数呈现扩大趋势。此时段为20世纪末21世纪初,我国城镇化正处于加速期,而我国人口快速增长是20世纪70、80年代,此时段城市建成区扩张速度快于城市人口增长速度,C选项正确。A选项人口城镇化增速变缓不符合我国实际;我国城镇人口增长峰期较早,故B选项错;我国城市用地峰期晚于城市人口增长峰期,故D选项错。由此可见,正确认识我国城市建成区面积与城市人口增长率的时段特征,才能正确分析数据,找出正确答案。
做题时不能只观察表面数据,应结合时间信息,从不同时段呈现的地理数据的特征入手,找出它们的差异,精准分析问题。
高考表格数据虽然复杂,但只要掌握了最基本的数据处理方法,从挖掘数据的隐性信息入手,学生就能够快速融入试题情境,从而做出正确判断。

