一种基于拉格朗日与时间解耦的超大规模SCUC求解框架
彭超逸,顾慧杰,周华锋,邱方堃,张淼,葛言
(1.中国南方电网电力调度控制中心,广州 510663;2.杉数科技(北京)有限公司,北京 100102;3.上海财经大学交叉科学研究院,上海 200433)
0 引言
随着电力市场改革逐渐进入深水区,特别是“双碳”目标的提出以及电力需求增速不断提高,在市场环境下电力供应系统的稳定、有效和安全运行变得越来越重要。安全约束机组组合(security constrained unit commitment,SCUC)是电力市场中最基本的优化问题之一,旨在满足电力系统安全性约束的条件下,制定多时段的机组开停机计划。2021 年,全国全社会用电量8.31 TWh,其中火电占比超过50%,燃煤机组启动过程的复杂性对于机组启停的决策优化提出了很高的要求。
SCUC 可以被建模为一个混合整数线性规划问题(mixed-integer linear programming,MILP),由于它是NP-hard 问题,很难找到高效快速的算法。一般而言,SCUC 问题的求解会在商业求解器中进行,但是对于超大规模的SCUC 问题,由于其具有大量的变量和跨期约束,直接调用求解器无法在合理时间内得到可行解,从而无法保障电力系统实时调度的准备时间,影响电力系统的正常运行。因此如何基于求解器设计一套泛用、高效的求解算法框架成为了目前研究的重要方向。其中混合整数规划、拉格朗日松弛法与分解算法是解决SCUC 问题的常用方法。
在混合整数规划相关方法中,国内外的研究基本围绕着减小问题规模的角度去设计相应的算法,尝试构造更加简洁紧凑的模型。在文献[1]中,作者提出了一种快速安全约束机组组合(fast security constrained unit commitment,F-SCUC)方法。该方法的核心思想是减少混合整数规划中整数变量的数量,通过在求解初期固定单元的状态,削减问题的规模,若固定状态后的模型无解,则逐步将固定的状态调整成变量,纳入模型进行求解,该方法能有效提升计算效率,但准确性欠佳。文献[2]尝试通过引入辅助优化问题,建立安全约束失效的具体条件,识别无效的安全约束,从而减小SCUC 问题的规模、提高求解效率。文献[3]将凸包理论从单机组场景拓展到多机组场景,利用线性规划来近似混合整数规划问题,提高了大规模电力系统组合模型的求解效率。文献[4]将机组系统建立成0-1变量的混合整数二次规划问题,采用启发式算法减少目标机组数目,缩小优化空间,并将处理后的模型利用有效集割平面算法进行求解。文献[5]建立了一种包含4 类0-1 变量的机组组合混合整数规划模型,提出了简洁的启动费用线性公式与机组出力约束公式,缩小了最优解的搜寻空间,有效提高了求解效率。但是一般而言混合整数规划在求解大规模SCUC 问题时往往不能在较短的时间内得到有效的解,需要借助其他方法进一步降低问题的难度。
本文采用的拉格朗日松弛方法也是一种有效的方法,其基本原理是将对问题求解造成困难的约束吸收到目标函数中,得到相对容易解决的拉格朗日松弛问题[6]。它的最优值为原问题最优值的提供了一个界,其质量将会部分依赖于吸收到目标函数中所选取的参数。拉格朗日松弛方法于1970 年被文献[7]提出,其应用范围包括了十几种最困难的组合优化问题,使解决大规模问题成为可能。文献[8]和文献[9]分别提出了基于拉格朗日松弛方法的快速算法对机组组合问题与电网布点及容量规划问题进行求解。
虽然线性的拉格朗日松弛方法能够以迭代的形式避开复杂约束加速求解,但是在大规模的复杂问题中传统的拉格朗日松弛方法会存在收敛困难的情况,特别是在最优解附近会存在震荡现象。为了解决这一问题,文献[10]在1995 年提出了在拉格朗日松弛问题的目标函数中引入二次项。由于序列二次 规 划 问 题(sequential quadratic programming,SQP)在求解时收敛性更强,因此该方法成功解决了传统拉格朗日方法长时间不收敛的问题。虽然拉格朗日松弛方法可以解决难解约束以及收敛性问题,但是由于问题规模过于巨大,仍需进一步使用分解算法来缩小问题规模。
现有的SCUC 分解算法大都是基于地理位置以及应用场景进行分割。文献[11]利用渐进对冲算法(progressive hedging algorithm,PHA)将问题按照不同场景进行分割求解。文献[12]开发了一套协同并发搜索技术和基于场景的分解技术,分别用于计算确定性情况与随机情况下的每小时日前机组组合(hourly day-ahead unit commitment)。文献[13]利用基于场景的分解算法来解决两阶段随机机组组合问题。文献[14]利用Benders 分解将SCUC 问题分解成了一个主问题和若干子问题并将应急约束考虑在内。文献[15-17]按照地理位置将SCUC 问题分解成若干子问题,并使用并行算法来协调各个子问题。文献[18]总结了电力系统分区与解耦相关的研究,基于地理位置与拓扑结构对各类分区准则进行了汇总与评述,并指出当前较优的方法为快速解耦与相序解耦。文献[19]运用基于多目标差分进化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D)和多目标蚁群优化算法,将优化问题分解为多个子问题分别进行蚁群算法求解,动态生成分区方案,并使用二代非支配排序遗传算法(non-dominated sorting genetic algorithmⅡ,NSGA-Ⅱ)求解最优解集。文献[20]将配电网按照馈线规模进行划分,作为独立的求解模块进行分区处理,并基于ZeroMQ 技术构建了分布式并行计算框架,在配电网节点超过500 个时具有明显速度优势。
上述文献从不同的角度将原问题分解成多个子问题,但是实际应用的SCUC 问题无论地理位置或者是馈线规模等都存在着巨大的耦合性,无法轻易进行分解。相对来说,从时间角度出发进行约束解耦是更优的方法。实际上时间解耦方法已经被广泛应用于电网动态无功优化[21]、风电机组-机械动态优化[22]等领域,但极少数文献考虑SCUC 场景下的时间解耦算法[23-24]。文献[25]利用拉格朗日松弛方法,通过将爬坡约束和最小启停时间约束等时间耦合约束放松,将原问题分解成若干子问题求解,并使用分支定界法寻找原问题的最优解。文献[26]考虑了潮流约束和网络安全约束,将问题分解为一个主问题与若干时段的子问题,分别处理机组的启停、出力与可行性校验,利用Benders算法进行协调。
最近有一些学者尝试将机器学习与鲁棒优化中的方法引入机组组合问题中。文献[27]从机组组合问题中的负荷曲线特征出发,将负荷水平聚类为有限个状态,建立了关于负荷状态转移的模型,从而有效削减了问题规模,提高了在中长期机组组合场景下的求解效率。文献[28]基于K-means 算法与长短期记忆(long short-term memory,LSTM)深度学习模型,试图利用历史数据刻画决策与系统负荷之间的关系,提高模型的适用性与求解效率。文献[29]基于鲁棒优化提出了嵌套式列生成的双层分解循环算法用于求解N-k故障约束的机组组合问题。文献[30]提出了一种多目标驱动的动态规划算法,能够实现跨时间的高效滚动规划,用于求解天然气与电力混合机组问题。文献[31]基于改进的Kmeans 算法,对运行初始场景进行缩减,并构建了两阶段机组启停模型。
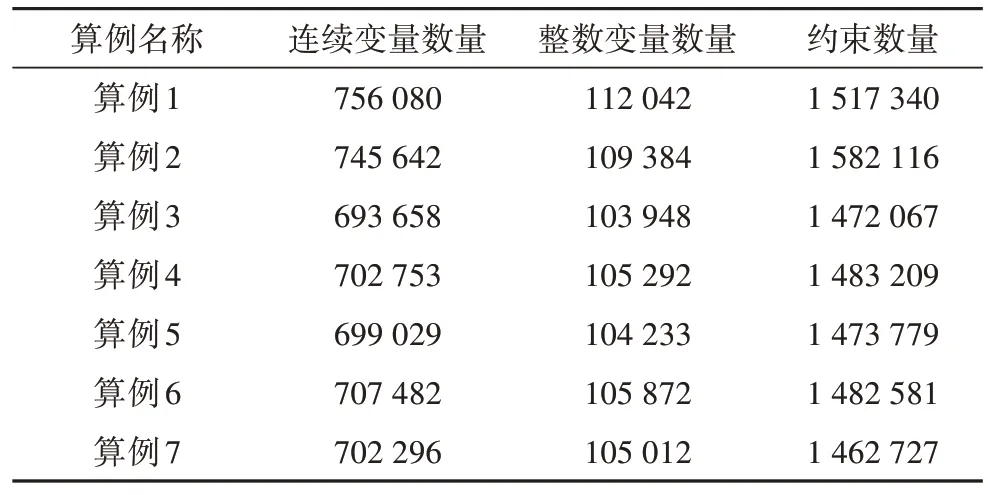
现有的方法大多存在两个问题:一是很多文献使用了经典数据集作为标准,传统经典数据集的规模较小,而实际生产环境中的求解规模要比标准数据集大将近8~10 倍,对于混合整数规划(mixedinteger programming,MIP)这种极度困难的NPhard 问题来说,标准数据集上的求解结果并不能够满足实际求解需求;二是在关注到时间解耦算法的文献中,大部分都引入了一些二次项惩罚以连接各个子问题模块,而这种二次项在超大规模的MIP中是不可接受的。
本文提出了一个线性化的解耦框架,并使用改进的拉格朗日松弛方法进一步加速SCUC 问题求解。线性化的时间解耦框架主要可以根据时间维度将问题分为多个子问题依次求解,减少求解时间;而改进的拉格朗日松弛方法能够处理稠密耦合性强的复杂约束,提升整体求解效率和保证一定的最优性。下文将详细介绍SCUC 模型、改进拉格朗日松弛方法和线性化的时间解耦框架,并通过数值实验来说明算法的有效性。
1 模型介绍
本文针对区域电力市场日前出清模型展开了研究,日前电力市场与实际运行情况较为接近,其出清结果对市场交易和系统运行均具有重要意义[32]。本文在参考文献[33-35]的基础上建立了模型,由于日前出清市场目前实际场景下使用的是每日96个决策区间,因此求解的决策颗粒度为15 min。在日前市场的出清中出清目标最优与求解效率提升均为算法考虑的范畴。
1.1 变量
本文涉及到的变量类型如表1所示。

表1 变量描述Tab.1 Variables description
1.2 目标函数
目标函数为电网总体运行成本的最小化,电网的运行成本包括发电成本、弃水成本和违反断面约束惩罚具体如下。
发电成本FP和弃水成本FW的计算如下。

机组发电量与单价的关系如图1所示。
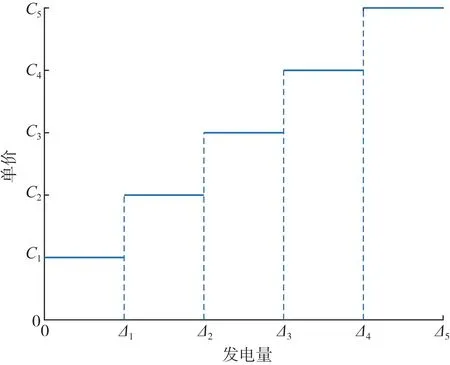
图1 机组发电量与单价关系示意图Fig.1 Schematic diagram of the relationship between generating capacity and unit price
1.3 约束
本文的SCUC 模型大部分采取了较为经典的建模方式[33-35],主要涉及的约束如下所示。
1.3.1 备用约束
备用约束指的是某个省开机的机组要比当前该省发电机总出力留有一定量的向上和向下调节能力。

1.3.2 机组与联络线组爬坡约束
对于火力发电的机组,机组发电功率在上/下爬坡时,均应当满足其爬坡速率要求。对于联络线组,其在某个时间点出力需要受到相邻时间点的出力值的影响。与机组爬坡不同的是联络线组爬坡需要考虑最小爬坡与最大爬坡,下爬坡和上爬坡都是同一个值,即需要引入向上爬坡和向下爬坡的两类变量。

1.3.3 机组与联络线出力约束
机组开机时有出力的下限和上限,关机时出力为0,在某些时间指定为关机状态并且不发电;水电机组需要考虑振动区,即出力区间是分段的。对于联络线,若某时间点不存在于拓扑中,则出力上界和下界均为0;若属于自由变化方向的类型,则上下界需要体现出方向(正负)的信息。
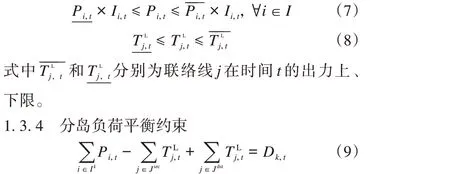
式中:Dk,t为电气岛屿k在时间t的电量负荷;Ik为电气岛屿k中的机组集合;Jsrc为送端联络线集合;Jdst为受端联络线集合。某个电气岛屿中所有的发电机的出力总和-该电气岛屿输送出去的电量+该电气岛屿接受到的电量=该电气岛屿的电量负荷。
1.3.5 机组开关机决策
式中:I为机组集合;Noni和Noffi分别为机组i所允许的最大、最小开机次数;Tu,i为机组i的最小持续开机时间;Td,i为机组i的最小持续关机时间;Igas为燃气机组集合;Nig为燃气机组ig中包含的机组数量。机组状态与决策相容(仅在关机状态下才能做开机决策,反之亦然),机组单日启停次数、最小连续启停时间限制在给定范围内,处于相同燃气机组群的燃气机组保持同启同停。
1.3.6 水电相关约束

下述几条约束为稠密和复杂的安全约束。
1.3.7 断面潮流约束
断面约束为电网中一个重要的安全约束的类型之一,其是否越限以及越限的程度都将严重影响电网运行安全的稳定。

1.3.8 线路输电约束
线路输电约束为电网中一个重要的安全约束的类型之一,其是否越限以及越限的程度都将严重影响电网运行安全的稳定。

1.3.9 交流联络线潮流约束
本文考虑多个区域的SCUC 问题。由于区域外的联络线传输功率一般由各区域间事先协商确定,这里提及的交直流联络线约束主要指的是区域内交直流联络线约束。交流联络线原本是非线性建模,为了让交流联络线参与建模,我们将其线性化和近似化表示。
交流联络线潮流安全约束是指在任意时间点,交流联络线拥有拓扑结构,不能像直流联络线一样进行自由优化,需要受到拓扑结构中的机组、直流联络线和负荷的影响。
在日常实际求解中,需要在求解完毕后校验断面、交流联络线潮流约束,如果存在违反,则相应调整上下限重新求解。本文更加关注SCUC 的MIP形式本身求解,调整约束上下界对于求解问题本身难度变化几乎为零,因此在本文中不作详细介绍。
断面潮流和交流联络线潮流这两类约束对于求解器存在着巨大的求解困难。求解器开发者曾经提出一个观点,在构建模型时要尽可能地避免构造出稠密的系数矩阵,一般以20 个非零元左右为界。而上述的两条约束对大规模电网而言,集合了几乎所有与电网相关的设备,远远高于20个非零元。在实际求解中我们也发现,正是因为这两种约束,大大增加了问题求解的难度。因此针对这种情况,本文提出了一种基于拉格朗日迭代的SCUC算法框架。
2 算法介绍
2.1 时间解耦算法
2.1.1 算法框架
尽管地理区域、不确定性场景和应急场景的分解可能会减少SCUC 的计算时间,但它们无法处理源自时间约束的计算复杂性。这种复杂性随着调度间隔数量的增加而增加。考虑调度间隔之间的偶然性和相互依赖性会增加SCUC 的计算时间。因此在考虑的调度时间范围内分解SCUC 可能是比地理分解更有前途的策略。
时间解耦的方法在工业界实践中已经被证明为最为有效的分解思路之一,在诸多不同工业场景下诸如工业排产,列车排班等等场景中往往可以提高近百倍的求解效率,同时最优求解的gap 可以有效确保在0.1%左右,完全能够符合日常排产的精度要求。上述SCUC模型可以表示为如下形式。
式中:I、P、T分别为机组开关、发电出力、传输功率的变量;Dscuc为问题的可行域。本文将总体的时 间 区 间T={1,2,…,n} 分 为k段Ti={ti-1,…,ti- 1},i= 1,…,k,其 中,1 =t0≤t1≤…≤tk=n+ 1。考虑如下分割:
式中:Ii、Pi、Ti分别为属于分段Ti的开关机组、发电出力、传输功率的变量;Di为只含有Ti中变量的约束集合;Doverlap为存在跨越时间段约束的集合。
我们考虑按照给定顺序T1,T2,…,Tk求解下列子问题。
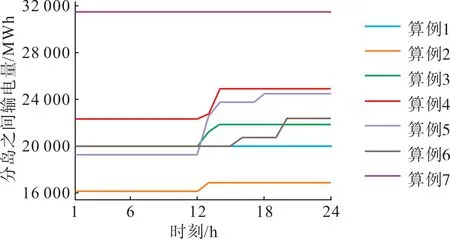
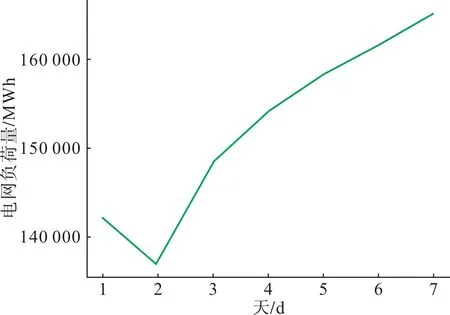
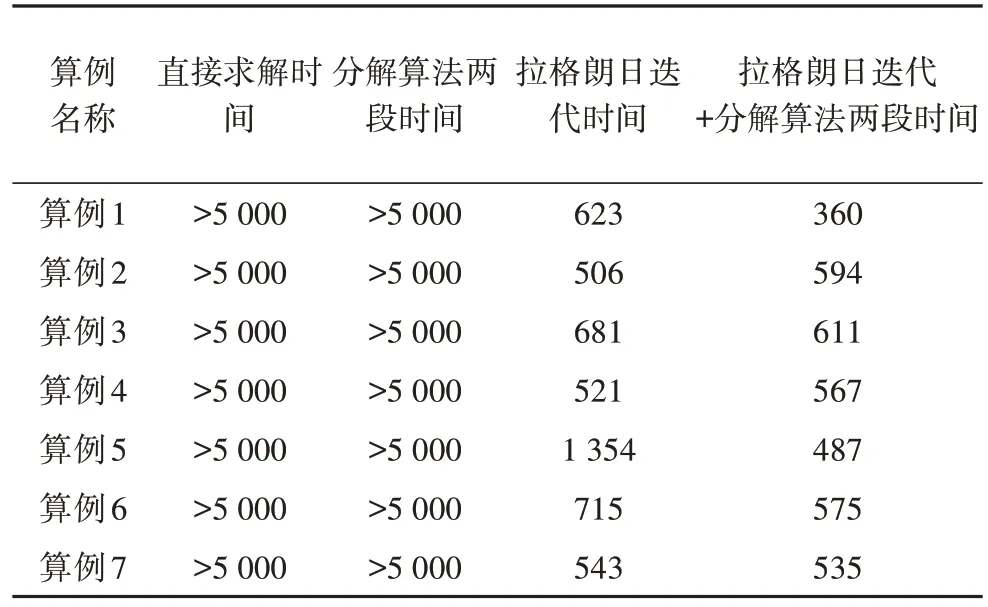
对于Optj,j 时间解耦算法遵循以下几个步骤。 1) 根据上面所定义的问题,构造出Ti对应的子问题,同时初始化队列; 2) 首先求解处于队列第一的T1对应的子问题,由于不存在其余的Optj,j 3) 根据解出的Optj,j 4) 将得到的解进行拼装即可得到严格可行的I、P、T。 时间解耦求解框架如图2所示。 图2 时间解耦求解框架Fig.2 Framework of time decoupling solution Doverlap中主要包含以下两类约束,分别具体处理如下。 1) 机组开关机决策 在该类约束中,都存在着机组开关机决策变量I跨越时间分段的情况,因此在求解问题Opti时,需要固定Ij,j= 1,…,i- 1 这些变量,这些变量先于Opti已经解出。在求解完Opti后下一个问题中需要进一步固定Ij,j= 1,…,i求解Opti+1。 2) 机组与联络线组爬坡约束 在该类约束中,跨越时间分段的主要有两种变量:发电出力变量P和传输功率变量TLG。处理方法同1)。 2.1.2 全局最优性约束 在实际算例求解中,由于约束之间耦合性较强,框架中直接对子问题进行分别求解可能会过分忽视子问题之间的关联性,造成框架求解最优性被严重破坏。因此,需要在解耦框架之上增加一种全局性的提示。 考虑一个原问题的近似问题如式(21)所示。 式中D′scuc的形成遵从以下几个规则。 1) 所有的整数变量松弛为连续变量; 2) 第1节中除断面潮流约束和交流联络线潮流约束外,其余的约束不作改动; 3) 在断面潮流约束以及交流联络线潮流约束中采样部分约束,除保留指定关键断面以外,其他约束采用随机抽取的方式。 这种随机抽取的方式并不会影响求解全局问题,其重要原因在于容易违反的断面约束几乎完全集中在关键断面之中,这些关键断面是结合日常生产经验以及一些启发式算法共同得出的,实践中这种随机抽取并不会引起过多的其他约束的违反。同时,在计算效率上,后续的拉格朗日框架中由于所有断面约束均统一加入了惩罚,问题形式不会有太大的变化,并不会引起求解效率的降低。 由此,问题的求解难度显著地下降。原因如下:1)整数变量被松弛,使原问题成为了线性规划问题;2)难以求解的断面以及交流线约束数量减少。但与此同时,问题的求解并没有损失太大的最优性。由式(21)得到的解(I′,P′,T′)添加一个全局性的正则项惩罚,构造以下问题。 式中λglobal为全局惩罚参数。本文通过构造1-模惩罚的方式将全局最优性纳入了框架考虑中,注意到这种惩罚函数的形式仍然为线性的,只是目标函数的形式发生了变化,因此时间解耦框架依然适用,且更接近最优解。 经过上述算法迭代后子问题虽然已经大幅度降低了规模,但是求解仍然会存在困难,这是由于子问题本身存在着难以求解的约束。考虑导致子问题求解困难的两类约束:断面潮流约束以及交流联络线潮流约束。 基于拉格朗日松弛迭代的SCUC 模型的算法具体流程如下。 1) 定位出SCUC 模型中稠密的耦合性约束,如SCUC 模型中的断面潮流约束和交流联络线约束,初始化对偶拉格朗日乘子, 跳至2)。 2) 根据拉格朗日松弛的原理,将以上耦合约束通过拉格朗日乘子加入到目标函数中,生成拉格朗日对偶问题,第ν次迭代中具体形式如下所示(以断面潮流约束为例)。 5) 判断式(23)迭代是否达到收敛(Oν+1-Oν≤σ),若达到收敛条件,则跳至6);若未达到收敛条件,则跳至3)。 6) 在SCUC 模型求解中使用拉格朗日迭代为子问题带来了重要的改进,这是由于去除了这两类极为稠密的约束后,原问题的稀疏性得到了极大的恢复。同时添加在原问题的目标函数上的惩罚项并不会过度地影响问题的数值稳定性,因为本文会通过δ控制惩罚项的量级,以确保原问题的最优性不会被破坏。 由于潮流约束越限数量决定了电网日常运行的稳定性程度,因此在问题(23)的迭代结束后若仍有部分断面越限,则还需要将这些越限的断面通过松弛惩罚的形式加入到SCUC 模型的目标函数中,并将第ν个问题(23)求解后未越限的断面以硬约束的形式加入到模型中,求解MILP 问题,跳至7)。MILP问题具体如下所示。 以上两部分算法使得原始超大规模的问题线性化的拆解成为了多个子问题,与此同时,针对稠密困难的约束,设计了一种线性化的松弛方案。与传统拉格朗日迭代不同的是,这种松弛方案多考虑了一步由线性松弛问题到原问题的一个近似MILP 的转换,以企图在不损失大量精度的情况下快速求解这个超大规模的SCUC 问题。下一章数值实验将阐明该求解框架的有效性。 本文选取了我国实际的某区域日前电力市场场景连续7 d 的真实算例,算例统一分为2 个分岛。图3 为分岛之间需要的输电量。图4 展示了整个电网系统每日总负荷情况,可以看出随着负荷上升分岛之间输电量一般呈正比关系。 图3 分岛之间输电量Fig.3 Power transmission between islands 图4 电网负荷Fig.4 Power grid load 表2 展示了电网部分运行参数。可以看到,电网存在一部分常量,如机组的数量。同时算例之间也有不同,如断面的数量。 表2 电网部分参数Tab.2 Partial parameters of power grid 综上,可以看到,目前本文所需要求解的具体问题规模庞大,难度极高,一般标准数据集难以企及。 我们采用python 语言编写程序,在CPU 型号为64 核,Intel(R) Xeon(R) Platinum 8 356 H CPU@3.90 GHz,内存为256 G 的设备上进行了实验。本文将根据发电成本、断面越限量以及计算时间来衡量算法的稳定性。在分解算法方面,本文分别比较了分段数为1(不分段)和2(分为两段)的求解效果,而对于拉格朗日迭代,本文则比较了使用前后的计算效率。各算法参数系数设置如表3所示。 表3 参数设置Tab.3 Parameters setting 3.2.1 求解效率对比 实验共展示7 个实时日前算例求解效率,这7个日前出清问题的问题规模如表4所示。 表4 问题规模比较Tab.4 Comparison of problem sizes 以上7 个算例都属于百万级别的数学规划问题,对于商业求解器而言,这已经属于较难求解的范畴,因此单纯求解问题本身已经非常困难,加上数值问题,导致了直接使用求解器几乎不可能完成这样的数学规划求解。因此另外单独使用了拉格朗日迭代算法以及分解算法进行求解,求解效率结果如表5所示。 表5 算法求解效率比较Tab.5 Comparison of algorithm solving efficiencies s 由表5 可见使用了分解算法后子问题的求解仍然会存在困难,而拉格朗日迭代算法由于巧妙地规避了求解器可能遇到的数值问题,求解迅速,在原始不能求解的问题上获得了巨大的效率提升。拉格朗日迭代算法加入了分解算法之后,问题的求解变得更为稳定,且用时更短。最好的情况下,在部分拉格朗日迭代问题上获得了近3 倍的提速,如算例5 由于输入参数的原因,导致求解器构建的问题数值情况不佳,但是分解算法由于缩减了子问题求解规模因此很好的抵消了数值问题带来的影响。 3.2.2 求解结果对比 本文还比较了两者最优性的情况,通过比较两者目标函数值的差异来证明算法的有效性,具体结果如表6所示。 表6 目标函数值比较Tab.6 Comparison of objective function values 由表6 可见两种算法求解结果相近,在算例4与7 中,分解算法甚至获得了比拉格朗日迭代更好的目标函数结果,这是由于λglobal的统一设置以及拉格朗日迭代本身带来的最优性损失使得算法并没有收敛到全局最优点,而分解算法在此时则有可能更为接近全剧最优解。 在此必须要指出SCUC 问题目标函数的近似下界也是很难给出的。两者给出的上界结果相近,实践中可以认为两种算法都已经得到了接近全局意义上的上确界,这也证实了算法的有效性。同时由于直接求解无法在合理时间内得到最优解,而分解算法两段直接求解也与其他可算算法的目标函数值比较接近,在一定程度上接近最优解。 3.2.3 数值实验总结 表7 给出了两种算法的表现,数值实验证明,两种算法的结合能够更加快速地求解超大规模SCUC出清问题,且求解更为稳定。 表7 算法表现比较Tab.7 Algorithms performance comparison 一般而言实际场景中的超大规模SCUC 出清问题直接使用求解器进行求解非常困难,因此本文从求解器求解难点出发提出了两种算法:1)以降低求解规模为目的的时间解耦算法;2)一种能够降低模型稠密度的拉格朗日松弛算法。同时,针对这类超大规模问题构建了基于这两种算法的求解框架。 数值实验证明,基于时间解耦以及拉格朗日迭代的算法在不损失较大精度的情况下获得了极大加速,满足了实际业务需求,为区域电力现货市场提供了有力的技术支持。 未来还可以开展更进一步的工作:一方面,实验发现,尽管大部分情况下分为多段求解会获得更高的效率,但是少数情况求解会出现不稳定的情况,因此如何确定优化分段也可以作为一大研究方向;另一方面,尽管得到的解已经较优,分解算法的最优性仍然存在优化空间,如果能够考虑分段之间求解的交互,而非完全独立,那么最优性可以获得进一步提升。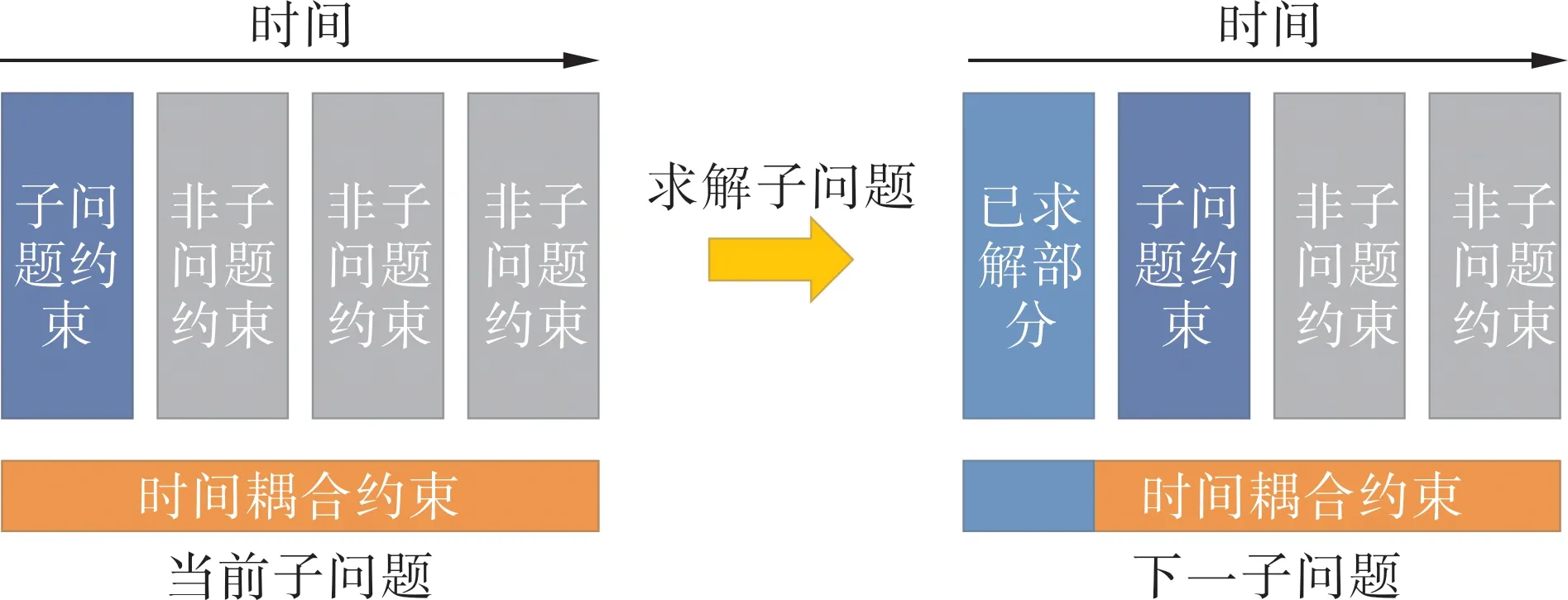
2.2 针对网络安全约束的拉格朗日松弛迭代


3 数值实验
3.1 数据介绍

3.2 参数设置及计算结果分析



4 结语

