考虑碳市场交易的寡头电力市场均衡分析
邓盛盛,陈皓勇,肖东亮,黄宇翔,余哲轩,曾鑫
(1.广东电网有限责任公司广州供电局,广州510620;2.华南理工大学电力学院,广州510641)
0 引言
温室气体的大量排放使生态环境日益恶化[1-2],采取必要措施以减少温室气体排放已成为世界上绝大多数国家的共识[3-4],我国政府也于2020 年9 月明确提出了2030 年“碳达峰”与2060 年“碳中和”的碳减排目标。目前碳减排机制主要有碳税制度[5-7]和碳排放权交易制度[8-10],后者以其市场化的机制实现了碳减排资源的优化配置,能以较低的成本控制碳排放[11],正受到越来越多国家的青睐。
2020 年12 月我国生态环境部正式印发了发电行业全国碳排放权交易配额总量设定与分配实施方案,2021 年7 月我国碳排放权交易市场(以下简称碳市场)正式开市,发电行业成为首个纳入碳市场的减排行业。根据制度安排,政府对纳入配额管理的发电行业重点排放单位碳配额总量进行设定与分配,各排放单位实际碳排放量大于其所分配碳配额数量的,可通过参与碳市场购入碳配额以满足履约要求。而对于实际碳排放量小于其所分配碳配额数量的,可通过参与碳市场出售多余的碳配额获利。
在新的背景下发电商需同时在电力市场和碳市场上进行交易决策[12],电力市场均衡状态也将受到发电商碳市场交易所影响。在电力市场均衡研究方面,文献[13]研究了考虑电动汽车的电力市场均衡模型,结果表明电动汽车参与电力市场可以使社会福利增加。文献[14-15]研究了绿色证书交易对电力市场均衡的影响,结果表明发电商在绿色证书市场上的策略性行为会抬高电力市场价格。文献[16]研究了固定电价制与可再生能源配额制对发电商决策及电力市场均衡的影响。然而,在考虑碳市场交易对电力市场均衡状态的影响研究方面,目前文献还比较少涉及。
文献[17]基于经典的古诺博弈竞争模型考虑了燃煤、燃气、水电等不同类型发电商,研究了碳排放成本对电力市场均衡状态的影响,但单位碳排放成本为假定的固定值。文献[18]在伊比利亚电力市场和西班牙碳减排计划框架下提出了一种考虑碳排放超标风险约束的发电商电力市场投标模型,但其考虑的仅为碳排放约束。文献[17-18]均未涉及发电商参与碳市场交易。文献[19]则考虑了电力网络约束,建立了碳市场背景下的电力市场双层均衡模型,但该模型中仅以碳排放总量约束和固定的碳排放成本来模拟碳市场所带来的影响。文献[20]在碳市场背景下提出了一种发电商参与电力市场投标的随机规划模型,但在该模型中碳市场及电力市场价格均由历史数据进行场景缩减形成。文献[19-20]所构建模型不能表征电力市场与碳市场的耦合关系及相互影响。文献[21]建立了考虑碳市场的电力市场古诺-纳什均衡模型,分析了碳市场交易对发电商在电力市场上的竞争策略的影响,但该模型假定碳市场为完全竞争市场,并没有考虑发电商在碳市场上的策略性行为。
总的来说,目前相关研究考虑碳市场交易的还比较少,尤其未涉及到发电商在碳市场上的博弈行为对发电商及电力市场均衡状态的影响。随着“碳达峰”与“碳中和”目标的提出及新型电力系统的建设要求,我国电力市场及碳市场建设正逐步向纵深推进。电力市场与碳市场之间存在着紧密耦合的关系,发电商在碳市场上的交易行为将对电力市场产生重要影响,因此研究碳市场及电力市场中发电商的交易决策及两个市场之间的交互影响关系,对于分析和改进市场机制,协同推进电力市场及碳市场建设具有重要意义。
本文从发电行业出发建立了一个考虑碳市场交易的寡头电力市场双层均衡模型,上层模型为各发电商以自身利润最大化为决策原则进行电力市场和碳市场上的交易决策问题,下层模型则包含电力市场出清及碳市场交易两个子模型,该模型可同时考虑发电商在电力市场和碳市场中的博弈行为。本文所建立市场均衡模型可以归结为一个具有均衡约束的均衡规划问题(equilibrium program with equilibrium constraints, EPEC),针对所提模型本文采用协同进化算法进行市场纳什均衡的求解。最后通过算例重点研究了碳市场对电力市场均衡及发电商市场博弈行为的影响。
1 基本假设
1.1 电力市场假设
考虑所有发电商各仅有一台机组,若拥有多台机组亦可折算为一台。假设发电商发电成本函数为二次曲线,如式(1)所示。
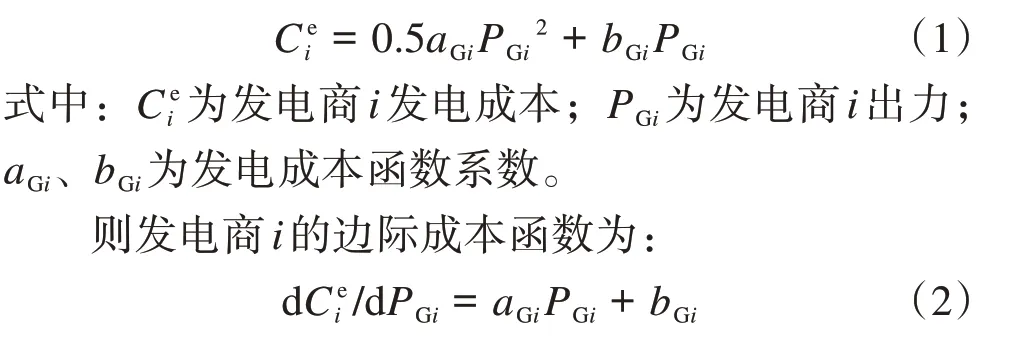
在完全竞争的电力市场中发电商通过申报真实的边际成本函数参与市场竞争。但在寡头电力市场中,发电商为寻求自身利益最大化[22],所申报竞价函数与其真实边际成本函数并不一致[23],因此本文假设发电商通过申报如式(3)所示竞价函数参与电力市场竞争。
式中:pi(PGi)为发电商i在出力PGi下的报价;ΔbGi为竞价增量,为发电商i参与电力市场的决策变量。应当指出的是发电商的竞价函数可以是对其边际成本函数的其他仿射变换形式,相应的决策变量也可以不同,但对本文相关分析不产生实质影响。
同理,对于电力用户而言其用电效用函数可表示为:
式中:Dj为电力用户j的用电效用;PDj为电力用户j用电量;aDj、bDj为用电效用函数系数。
则电力用户j的边际用电效用函数为:
本文假设电力用户通过申报真实的边际用电效用函数参与电力市场竞争,暂不考虑电力用户在电力市场上的策略性行为。
1.2 碳市场假设
根据国家发布的发电行业碳排放权交易配额总量设定与分配实施方案,发电行业初始碳配额采用基准线法免费分配,由监管机构规定单位供电量的碳排放基准值来控制发电商碳排放量。假设对于碳排放系数大于碳排放基准值的发电商(以下简称高排放发电商),须在碳市场上足额购买缺少的碳配额以满足碳配额履约要求。而对于碳排放系数小于碳排放基准值的发电商(以下简称低排放发电商),以多余碳配额的交易比例ui作为决策变量在碳市场上出售碳配额获利。
碳市场中碳配额价格受供需关系所影响,当ui< 1 时,意味着低排放发电商选择持留部分碳配额以操纵碳市场价格,当ui= 1 时,则可认为发电商在碳市场上无策略性行为。借鉴文献[24-25],假设碳配额价格满足如下函数关系。
式中:λc为碳市场碳配额价格;d为高排放发电商碳配额总需求量,亦即为高排放发电商碳配额总购入量;s为低排放发电商碳配额总出售量。需特别注意的是,高排放发电商碳配额总购入量不必等于低排放发电商碳配额总出售量,原因在于碳市场中市场主体除发电行业外还包括其他行业,因此不必保证单个行业碳配额供需平衡;β为发电行业碳配额净需求量(即d-s)对碳市场碳配额价格的影响因子;λ0c为发电行业碳配额净需求量为0(即d-s= 0)时的碳市场碳配额价格。β及λ0c可通过历史数据进行回归法[26]分析得到。
式(6)用一次线性函数关系表征了碳配额价格与供需之间的关系,碳配额虽然具有一定特殊性,但仍然满足一般商品的价格属性[27],即碳配额需求增加而供给减少时,碳配额价格升高,碳配额需求减少而供给增加时,碳配额价格下降。本文所假设的碳配额价格模型式(6)符合价格主要由供需所决定的市场规律[28]。
2 考虑碳市场交易的寡头电力市场均衡模型
本文中发电商通过申报竞价函数参与集中式的电力日前现货市场,电力交易机构在接收到发电商及电力用户申报的竞价函数后,以社会福利最大化为出清原则进行市场出清。碳市场为现货市场,发电商根据自身的碳配额需求或碳配额可供给量在碳市场上进行交易,碳配额价格由供需关系所决定。
本文通过建立上层模型为各发电商以自身利润最大化为决策原则进行电力市场和碳市场上的交易决策,下层模型则包含电力市场出清及碳市场交易两个子模型的双层模型来描述电力市场及碳市场间的交互影响关系及市场中发电商的交易决策问题。上层模型中发电商的决策依赖于下层模型所返回的电力市场电价和碳市场碳配额价格信息,下层模型电力市场出清及碳市场交易则依赖于上层模型中发电商的市场交易策略。
2.1 上层模型:发电商电力市场及碳市场决策
上层模型为发电商以自身利润最大化为决策目标进行电力市场及碳市场决策,在电力市场上所有发电商以竞价增量ΔbGi为决策变量,在碳市场上低排放发电商以碳配额交易比例ui为决策变量。发电商利润为售电收入减去发电成本及碳市场成本。对于低排放发电商,参与碳市场能够获得收益,此时碳市场成本为负值。则上层模型为:

2.2 下层模型1:电力市场出清
下层模型1 为电力市场出清模型,电力交易机构根据发电商及电力用户申报的竞价函数并计及电力供需平衡等约束,以社会福利最大化为目标函数进行出清,出清得到市场电价及发电商、电力用户的中标电量。下层模型1可表示为:

2.3 下层模型2:碳市场交易
下层模型2 为碳市场交易模型,在该模型中高排放发电商须全额购买与超额碳排放所对应的碳配额,而低排放发电商则以多余碳配额为出售上限,在碳市场上有策略性地决定碳配额出售比例。下层模型2可表示为:
式中:qmaxi为发电商i在碳市场上最大可交易碳配额数量,当其为正时表示需买入碳配额,为负时表示可出售碳配额;ξi、ξ*分别为发电商i碳排放系数、监管机构所确定的碳排放基准值;qi为发电商i实际交易碳配额数量。式(15)为发电商可交易碳配额上限约束,式(16)表示发电商实际交易碳配额数量,式(17)形成碳市场碳配额价格,式(18)为发电商碳市场成本(为负则为收益)。
2.4 电力市场和碳市场间的交互影响
根据2.1—2.3 节,本文所建立的碳市场与电力市场均衡模型如图1表示。
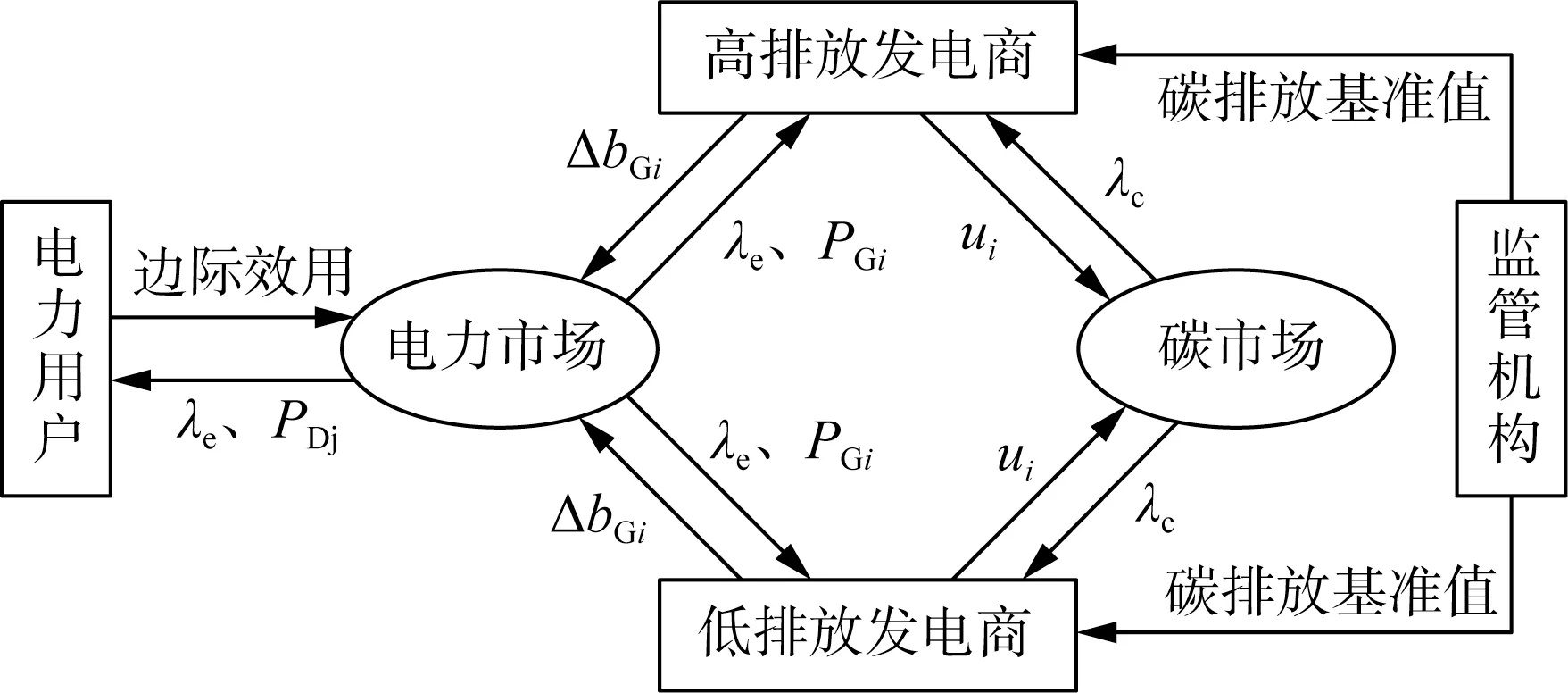
图1 碳市场与电力市场均衡模型Fig.1 Equilibrium model of carbon and electricity markets
在电力市场中所有发电商通过决策其竞价增量ΔbGi修正边际成本曲线以形成竞价函数参与市场竞争,而电力用户则申报真实的电能边际效用函数参与市场。电力交易机构根据发电商和电力用户所申报的竞价函数,以社会福利最大化为优化目标进行市场出清,形成出清电价及发电商、电力用户的中标电量,本文暂不考虑电力网络约束。
在碳市场中高排放发电商须根据中标电量在碳市场上全额购买超额碳排放所对应的碳配额,而低排放发电商则以中标电量所对应的碳配额盈余为上限,在碳市场上有策略性地进行碳配额交易比例决策,从而影响碳配额供给。碳市场价格由碳配额供需关系所决定,因此低排放发电商选择交易碳配额的比例ui及高排放发电商的碳配额需求均会影响碳市场碳配额价格。
低排放发电商在碳市场上对碳配额供给的操纵将影响碳市场碳配额价格从而影响高排放发电商的收益,高排放发电商在碳配额的约束下则会调整其在电力市场上的竞价策略,进一步对低排放发电商在电力市场和碳市场上的交易策略产生影响,因此各发电商的决策须同时考虑电力市场和碳市场的竞争情况,电力市场和碳市场之间存在着较为紧密的耦合关系。
3 协同进化算法求解市场均衡模型
3.1 求解流程
作为一种多群体智能算法,协同进化算法强调种群间的相互作用,能较好地模拟市场成员间的博弈和市场演化[29-30],因此本文采用协同进化算法求解所构建的市场均衡模型。求解流程如图2所示。

图2 协同进化算法求解流程Fig.2 Co-evolutionary algorithm solution process
2)步骤2:计算所有种群各个体适应度。以第k代种群i中各个体适应度计算为例,将种群i待评价个体j与其他各种群k-1代最优个体组成交易策略集合,形成相应的市场策略环境并进行电力市场及碳市场出清,得到发电商i利润Fk ij,并将Fk ij作为种群i个体j的适应度值。若j 3)步骤3:精英保留及种群更新。记录第k代各种群最优个体W k i,best,而后分别对各种群个体进行选择、交叉、变异操作,并将W k i,best替 换 新种 群最后一个个体,形成第k+1代种群。 4)若未满足收敛条件且k 发电商在市场中的竞争构成非合作博弈,由纳什均衡的定义,任一发电商i均以自身收益最大化为决策目标进行决策,当其他所有发电商(i′)都不改变策略时,任一发电商均不会单方面改变自身策略,否则自身收益Fi将降低,此时的市场状态就是一个纳什均衡状态,即满足: 本文采用协同进化算法求取市场均衡,若当多次迭代后各发电商利润进入稳定状态,发电商市场策略不再变化,则有: 又协同进化算法求取市场均衡,当迭代进入收敛状态时有: 将式(21)代入式(20)即为式(19)。因此当算法处于收敛状态时,此时市场为纳什均衡状态。 本文假设市场中共有发电商4 家,发电商参数如表1 所示,其中G1、G2 为高排放发电商,G3、G4 为低排放发电商。协同进化算法基本参数设置为交叉概率Pc=0.9,变异概率Pm=0.05,种群个体数量为Nsize=50,最大迭代代数为T=200,收敛条件参数设置为ϕ= 5,ψ= 0.1。设碳配额价格满足λc= 0.6(d-s) + 30,单位为美元/t CO2,碳排放基准值ξ*取为0.78t CO2/MWh。本文算例在一台2.3 GHZ、 4GB RAM 的个人计算机上使用MATLAB R2017a软件编程实现求解。 表1 发电商参数Tab.1 Parameters of power producers 4.2.1 市场均衡分析 协同进化算法求取市场均衡过程中各发电商利润变化情况如图3 所示,各发电商市场策略进化情况如图4 所示,其中图4(a)为发电商电力市场策略进化情况,图4(b)为低排放发电商碳市场策略进化情况。从图3—4 可以看出,在种群进化初期,发电商在电力市场及碳市场上的策略在不断地变化,发电商收益波动较为明显,原因在于发电商为实现自身利润最大化不断地对自身策略进行试探和修正,随着种群进化代数的增加,市场最终在70 代左右趋于均衡状态。 图3 发电商利润变化情况Fig.3 Changes in the profits of power producers 图4 发电商市场策略进化情况Fig.4 Evolution of market strategies of power producers 表2 为市场均衡状态下发电商相关情况。在市场均衡状态下,发电商中标电量G1>G3>G2>G4,而发电商收益G3>G1>G2>G4。原因分析如下:G3中标电量虽然低于G1,电力市场收益仅为G1 的87.6%,但作为低排放发电商的G3 通过在碳市场上出售碳配额获得了较高的碳市场收益,而高排放发电商G1 却须在碳市场上付出较高的碳配额购买成本,从而导致G3 最终收益高于G1。而G2 与G3相比,虽然发电商装机容量及发电成本参数均一致,但G2 为高排放发电商,由于碳排放约束的作用,须在碳市场付出相应减排成本,削弱了其市场竞争力,从而使得G2 中标电量及收益均低于G3。而G4 虽然碳排放系数最低,可在碳市场获得较多收益,但受限于其装机容量及发电成本,其最终收益仍为所有发电商中最低。 表2 市场均衡状态下发电商相关情况Tab.2 Relevant situation of power producers in the market equilibrium 4.2.2 碳市场对电力市场均衡影响分析 为分析碳市场对电力市场均衡的影响,本节考虑以下情形。 1) 情形1,无碳市场情形:发电商无碳排放约束,无须参与碳市场。 2) 情形2,考虑碳市场且发电商在碳市场有策略性行为情形:低排放发电商可通过策略性地决定卖出多余碳配额的比例以影响碳配额价格。 3) 情形3,考虑碳市场但碳市场为完全竞争情形:低排放发电商不再持留多余的碳配额,其在碳市场上的碳配额交易系数为1。 不同情形下市场均衡情况如表3 所示。首先对比分析无碳市场情形(情形1)与考虑碳市场且碳市场有策略性行为情形(情形2)。从表3 可以看到,考虑碳排放约束和发电商参与碳市场后,高排放发电商均选择增大其电力市场竞价增量,而低排放发电商电力市场竞价增量变化则并不一致。原因在于,对于高排放发电商而言,由于碳排放的制约须在碳市场上购买碳配额相当于增加了发电商发电成本,因此高排放发电商将选择提高电力市场报价,从而将碳减排成本尽可能传导至用户以减少碳排放约束对自身收益的影响,但相比无碳市场情形,G1、G2 收益分别下降了6.6%、8.8%。而对于低排放发电商而言,碳排放约束增加了市场竞争力,高排放发电商的部分出力将转移至低排放发电商。此时低排放发电商G3 和G4 间也存在博弈以争夺这部分“红利”。G4 在发电成本与碳排放方面相比G3均不占优势,因此选择报低价争取中标电量,而竞争力更强的G4则选择适当报高价以抬高市场价格,但无论选择哪种策略,低排放发电商的收益均得到较大幅度提高,G3、G4 收益分别提高了16.0%、17.7%。 表3 不同情形下市场均衡情况Tab.3 Market equilibrium in different scenarios 其次对比分析考虑碳市场且碳市场有策略性行为(情形2)与碳市场完全竞争情形(情形3)。从表3可以看到,发电商在碳市场上的策略性行为同时抬高了市场电价与碳价,减少了高排放发电商收益而增加了低排放发电商收益。原因在于低排放发电商通过在碳市场上持留碳配额降低了碳市场供给从而抬高了碳配额价格,增加了自身收益。而碳配额价格的抬高增大了高排放发电商的成本,促使高排放发电商提高自身电力市场报价,也因此减少了中标电量,导致高排放发电商收益下降。两种情形的结果对比也表明了市场竞争越充分则电价上涨的幅度就越小,即碳排放成本向用户传导的作用就越小。原因在于在高度竞争的市场环境下发电商不会选择过多的提高电力市场报价,否则其市场竞争力下降导致的利润下降将大于其向用户传导的碳减排成本,此种现象也将引导发电商更多地着眼于自身的碳减排升级改造而非一味转嫁成本至用户。 可以看到在碳排放基准值较高的情况下低排放发电商倾向于行使市场力持留部分碳配额以抬高碳配额价格,而在碳排放基准值较低的情况下低排放发电商则选择将多余碳配额全部售出。 4.2.3 碳排放基准值的灵敏度分析 图5 为不同碳排放基准值下发电商市场策略变化情况。从图5(a)可以看到,随着碳排放基准值的降低(即碳排放约束的收紧),高排放发电商G1、G2 在电力市场中的竞价增量均在不断上升,即不断提高电力市场报价。而低排放发电商的竞价增量变化并不一致,但变化幅度均相对较小。从图5(b)可以看到,在碳排放基准值较高的情况下,低排放发电商倾向于行使市场力持留部分碳配额以抬高碳配额价格,而在碳排放基准值较低的情况下,低排放发电商则选择将多余碳配额全部售出。 图5 发电商市场策略变化情况Fig.5 Changes in the market strategies of power producers 以上现象分析如下:碳排放基准值的降低将导致高排放发电商在碳市场上所需购买的碳配额增多,同时使得低排放发电商能出售的碳配额减少,碳市场供给减少而需求增加,因此使得碳价上升。碳价的上升又将进一步推高高排放发电商的成本,高排放发电商则会选择在电力市场上提高报价,虽然此举导致其中标电量下降,但是抬升了电力市场电价,也减少了其在碳市场上所需购买的碳配额数量,因此高排放发电商将选择抬高电力市场报价以最大化自身利润。 对于低排放发电商而言,在电力市场上会根据自身情况调整策略,如4.2.2 节所分析,竞争力稍弱的G4 选择适当降低报价争取中标电量,而竞争力更强的G3 则会选择适当提高报价以抬高结算价格。在碳市场上低排放发电商G3、G4 策略变化如图5(b)所示,原因在于碳排放基准值较高时碳市场价格较低,低排放发电商则有动力行使市场力持留部分碳配额以减少供给从而拉高碳配额价格,而在碳排放基准值较低时碳市场价格相对较高,此时发电商选择将全部多余的碳配额售出能够获得更高的利润。 图6为不同碳排放基准值下电价及碳价变化。 图6 市场价格变化情况Fig.6 Changes in market prices 正如上述分析,随着碳排放基准值的降低电价及碳配额价格均被不断抬高。另外注意到图6(a)中碳价由12.41 美元/t 上升至66.41 美元/t,而图6(b)中电价仅由59.39 美元/MWh 上升至61.85 美元/MWh,即电价的上涨远没有碳价上涨的幅度大,主要原因在于采用基准线法进行碳配额分配时碳排放基准值与各发电商的碳排放系数的差值通常并不大,如本算例中该差值绝对值的平均值仅为0.06 t CO2/MWh,即无论是高排放发电商还是低排放发电商,其单位发电量所需购买或可出售的碳配额均比较少,使得碳价上涨引起的电价上涨并不十分明显,另外一个原因则如4.2.2 节所述,不完全竞争市场中发电商间的博弈也将削弱碳排放成本的传导。 本文建立了一个考虑碳市场交易的寡头电力市场双层均衡模型,上层模型为各发电商以自身利润最大化为决策原则进行电力市场和碳市场上的交易决策,下层模型则包含电力市场出清及碳市场交易两个子模型,该模型可用于研究碳市场及电力市场中发电商的交易决策及两个市场之间的交互影响关系,得出以下结论。 1) 考虑碳市场后高排放发电商将选择提高电力市场报价,但最终收益均会下降。而低排放发电商电力市场报价策略的变化则取决于不同低排放发电商之间的市场竞争情况,但最终收益均会提高。 2) 发电商的策略性行为同时抬高了电价与碳配额价格,但市场竞争越充分,电价上涨的幅度就越小,即碳排放成本向用户传导的作用就越小。 3) 在碳排放基准值较高的情况下低排放发电商倾向于行使市场力以抬高碳配额价格,在碳排放基准值较低的情况下低排放发电商则会选择将多余碳配额尽可能售出。 4) 采用基准线法进行初始碳配额分配时由于碳排放基准值通常与各发电商碳排放系数相差不大,且受发电商间的市场博弈行为所影响,因此当碳减排政策收紧时,电价的上涨幅度将远小于碳价的上涨幅度。 未来将基于更加成熟的碳市场机制及更加丰富的市场运行数据进一步验证模型的准确性,同时在现有模型基础上进一步考虑电力网络约束及安全约束机组组合等相关因素,更为深入地分析电力市场及碳市场耦合下发电商的交易决策及两个市场之间的交互影响关系。3.2 纳什均衡判定


4 算例分析
4.1 基础数据

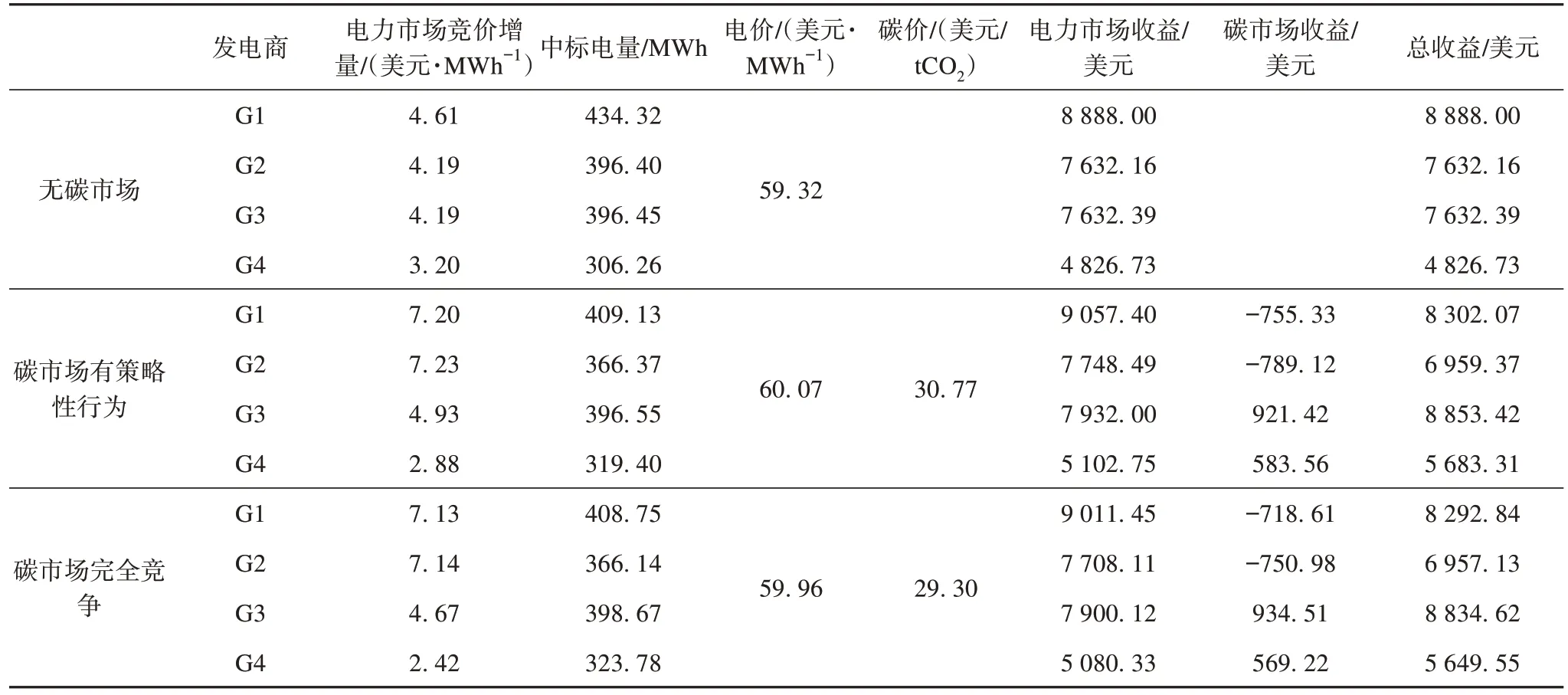
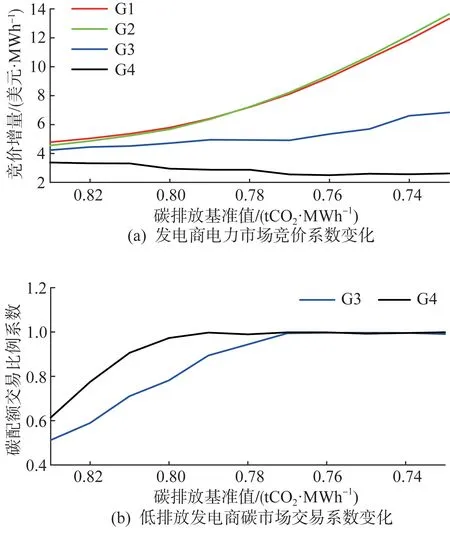
4.2 结果分析
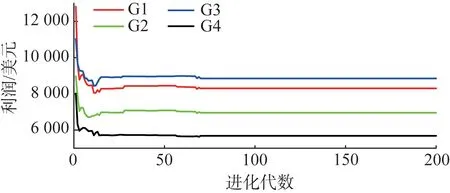

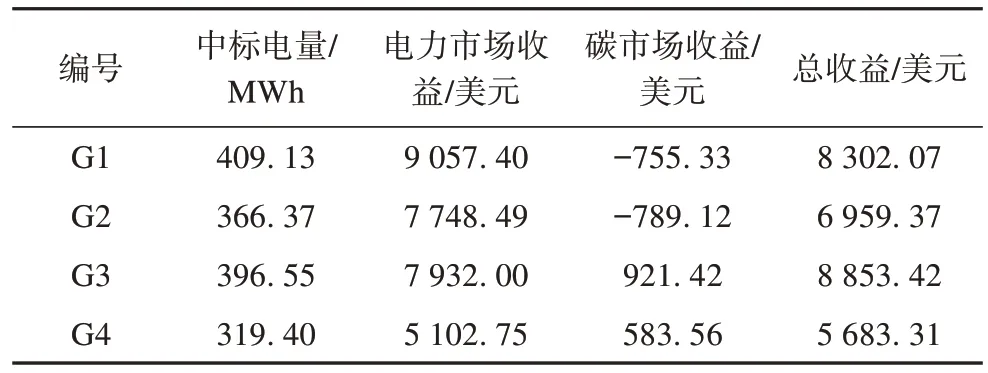

5 结论

