基于强化学习的电-气-热多微网系统定价策略

李媛，迟昆，王洲，彭婧，贾春蓉，刘炳文

（1.国网甘肃省电力公司经济技术研究院，兰州730050；2.西安交通大学电气工程学院，西安710054）

0 引言

在低碳减排的能源背景下，含电、气、热等的多能源微网通过整合多类能源，在提升能源利用效率、满足用户灵活多样的能源需求等方面展现出明显的优势［1］。未来电-气-热多微网的互联可形成规模化的电-气-热多微网系统。然而由于各类能源的复杂耦合，电-气-热多微网系统在规划、运行与管理等层面面临诸多挑战［2］。随着能源交易市场化，多微网系统可能由微网服务商、微网等诸多市场参与者共同管理。各市场参与者间的交易行为将影响系统的运行和各方的利益［3］。

现有研究已引入了不同的方法研究类似的市场交易。文献［4］研究了区域综合能源系统的交易策略，并建立了双层优化模型。文献［5］考虑了能源梯级利用以研究能源交易策略。两者都将双层模型转化为单层模型求解。文献［6-7］等研究使用博弈论来描述市场交易过程。但上述文献都采用集中式算法求解，考虑到市场环境下参与者之间的竞争与隐私保护行为，集中式算法难以实际应用。

因此，一些研究引入了启发式等算法以保护用户隐私。文献［8］采用了粒子群算法解决配电网与各微网间的斯塔克尔伯格（Stackelberg）博弈。文献［9］建立了三层优化问题，并采用遗传算法求解最上层问题。文献［10-12］等采用类似的启发式算法优化园区、微网的主从博弈定价策略问题。另外，文献［13］采用有效集法和最速下降法求解了综合能源微网交易策略，很好地保护了用户隐私。然而，对于大规模优化问题启发式算法难以保证求解效率，得到的可行解可能偏离最优解。有效集法等算法受限于复杂的数学形式，实用性较差。

相对而言，依赖于马尔可夫决策过程（Markov decision process，MDP）的强化学习算法以求解最优策略为目标，不易陷入局部最优，有更广泛的适用性。近年来，强化学习特别是深度强化学习（deep reinforcement learning，DRL）算法，在多能系统［14-16］应用广泛，能更好的应对系统的不确定性［17-18］。文献［19-20］证明了DRL 算法可兼顾用户隐私。除文献［21-22］外少有研究将DRL 算法用于求解类似博弈问题，文献［21-22］虽将斯塔克尔伯格博弈转化为MDP，但均未考虑时间耦合约束，然而现实中时间耦合约束是难以忽略的。因此针对所研究的定价问题，本文提出了一种基于强化学习的求解方法，以解决含时间耦合的斯塔克尔伯格博弈问题。

基于以上分析，本文首先描述了电-气-热多微网系统内部交易过程并建立了相应的系统模型。其次，微网服务商的定价策略问题被描述为斯塔克尔伯格博弈。可以证明，该博弈存在唯一博弈均衡点。针对这一问题，提出了一种基于强化学习的求解方法以保护用户隐私并提升求解效率。计算结果表明，该方法有效解决了含时间耦合约束的斯塔克尔伯格博弈问题，制定了符合各方利益的策略。

1 多微网系统模型

1.1 多微网系统结构

本文所研究的电-气-热多微网系统如图1 所示，包含了1 个微网服务商和N个电-气-热微网。考虑到微网服务商与各微网均为独立的经济实体，交易时各方均追求自身利益最大化。

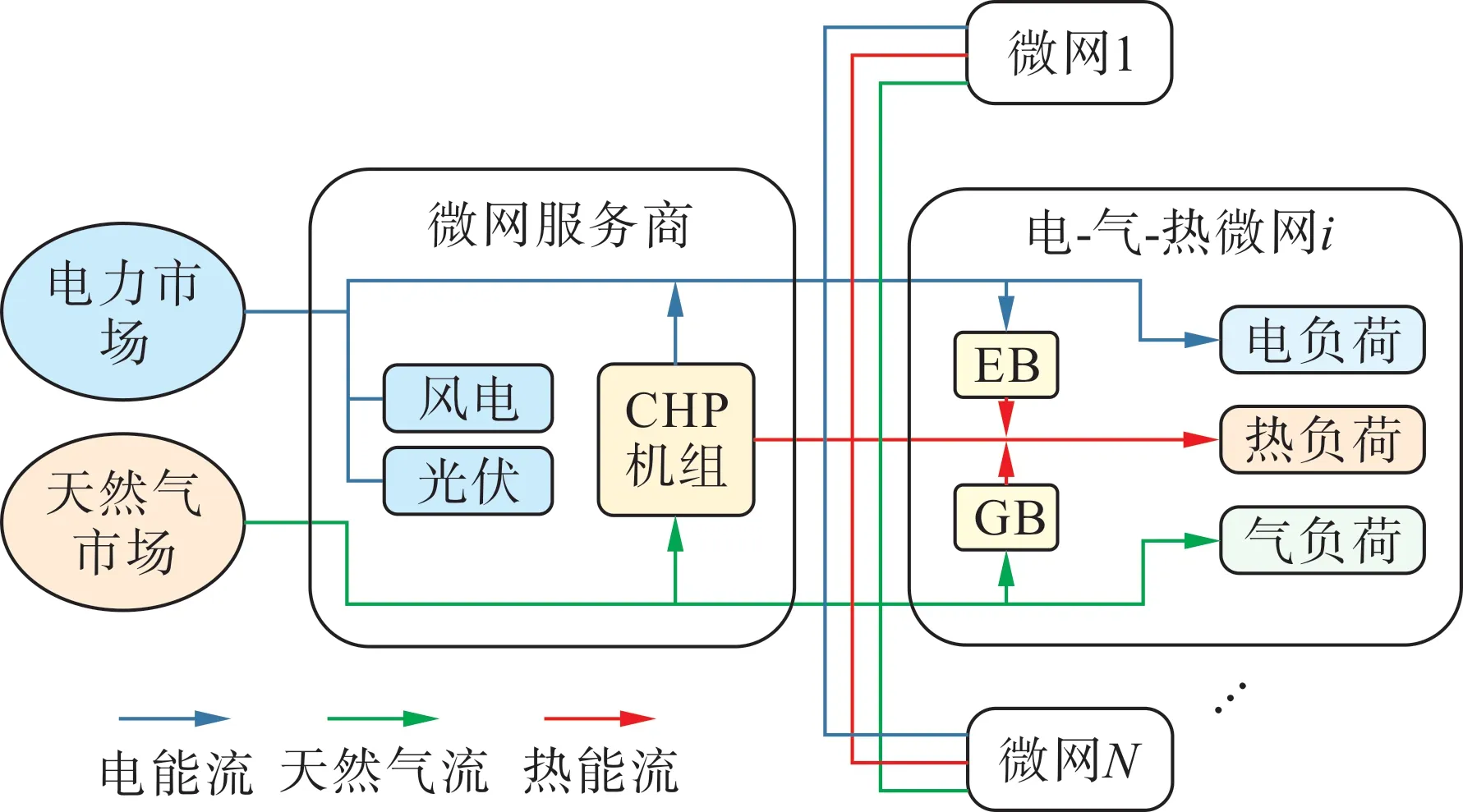
图1 电-气-热多微网系统Fig.1 Electric-gas-heat multi-microgrid system

微网服务商主要服务于配网层面，其向上可接入上级能源市场以购入电能、天然气，向下可连接区域内多个微网。微网服务商负责区域内配网的建设，其配备风电、光伏和热电联产机组等设备用以实现能源整合，同时制定零售价并向各微网供应能源以获取利润。

各电-气-热微网需从微网服务商购买能源以满足自身用能需求。各微网均参与综合需求侧响应，根据零售价调整自身策略，同时配备有一定容量的电锅炉（EB）、燃气锅炉（GB）设备以保证更经济灵活的热能供应。

本研究假定微网服务商不影响上级能源市场的价格。为保证可再生能源的消纳，微网服务商可向上级能源市场出售富余电能，但为避免问题退化，该问题只在多微网系统内部交易完成后考虑。

1.2 微网服务商定价模型

微网服务商首先制定电、气、热能零售价，并得到各微网反馈的购能信息。基于所得信息微网服务商进一步优化定价策略和运行策略。

1.2.1 目标函数

微网服务商的目标是最大化其全天净利润，如式（1）所示。第一项为售能收入，第二项为总成本，包括购能成本、设备运行成本。

1.2.2 约束条件

多微网系统需满足各类能源实时供需平衡。如式（2）—（4）所示，等式左侧分别表示电、气、热能的供应量，等式右侧分别表示各能源需求量。

式（5）—（8）为热电联产机组的运行约束。式（5）表示机组所消耗标准状态下天然气的体积，式（6）表示机组可输出的电功率限制，式（7）表示机组输出的热功率，式（8）为机组的爬坡功率约束。

式中：κa、κb、κc为热电联产机组成本系数；λe-h为机组输出热、电功率比例；Pchp，max为机组输出最大电功率；Pchp，rate为机组的最大爬坡速率。

式（9）—（11）为零售价格上下限约束，电、气、热能的零售价均应限制在合理范围内。

1.3 电-气-热微网优化模型

各电-气-热微网根据能源零售价，进行综合需求响应，并确定EB和GB的运行策略，以制定最符合自身利益的购能方案。微网模型可统一表示如下。

1.3.1 目标函数

电-气-热微网的的目标是最小化全天总成本，如式（12）所示。第一项为从微网服务商购能的成本。第二项包括需求响应成本和灵活供热成本。

1.3.2 约束条件

EB 设备需满足功率上下限约束和设备爬坡约束，如式（17）—（18）所示。

同样地，GB 设备需满足功率上下限约束和设备爬坡约束，具体形式类比式（17）—（18）。

电-气-热微网的实际购能量可由式（19）—（21）确定：

2 斯塔克尔伯格博弈

根据本文所研究的多微网系统模型，微网服务商与各电-气-热微网间存在如下交易过程：微网服务商首先向各微网报价；随后，各微网优化自身策略，以最小化总成本，并将购能量反馈给微网服务商；最后，微网服务商依据反馈结果调整零售价和相关运行变量。此交易模式决定了该定价问题可被描述为“一主多从”结构的斯塔克尔伯格博弈，其中微网服务商可被视为领导者，不同的微网可被视为跟随者，该博弈包含以下3个部分。

变电站改造期间临时供电模式的风险及预控措施初探…………………………………………… 李世博，赵红星（12-81）

1） 竞争者：包括1 个微网服务商和N个电-气-热微网，表示为P={MSP，{MG1，…，MGN}}。

可以证明，本文所提出的斯塔克尔伯格博弈存在唯一的博弈均衡点。

在达到博弈均衡点前微网服务商与各微网重复博弈的过程可被视为一类强化学习问题，即智能体代表微网服务商的利益不断与环境中各微网交互。为此，本文进一步研究了一种基于强化学习的斯塔克尔伯格博弈均衡点求解方法。

3 强化学习求解方法

现有研究将领导者视为智能体（agent），跟随者视为环境（environment），提出了相应的MDP［20-21］，利用强化学习训练智能体与环境交互，求解斯塔克尔伯格博弈均衡。但此类方法无法本文模型中存在的式（16）、式（18）等时间耦合约束，这些约束将破坏其MDP 的马尔可夫性。马尔可夫性可表示为式（22），是指环境的下一状态只与当前状态有关，而与先前状态无关。

式中：Pr［］表示［］中事件发生的概率。

因此本研究构造了一种新的MDP，以适应存在时间耦合约束的斯塔克尔伯格博弈。包括以下4个元素。

1） 状态：智能体观测到的环境状态。既包括微网服务商已有的信息，如风光机组出力、热电联产机组状态、上级能源市场的购买价格等；也包括各微网反馈的信息。针对某一确定的定价策略，每个微网都有唯一的最优响应，利用这一关系，可用定价策略唯一地表示微网的状态。因此，状态向量可表示为式（23）。

式中t包含包括所有仅与时间相关的状态信息；各类能源的定价策略则反映了各微网的状态。

3） 回报：智能体的目标应与微网服务商的目标函数一致，即时回报定义为式（25）：

式中：r1为时段1 的即时回报；rt为时段t的即时回报；(at，st)表示微网服务商基于at、st得到的完整定价方案；(s0)表示微网服务商的初始定价方案。

由式（26）可得，智能体总回报为：

4） 状态转移：首先，智能体确定某时段的动作值at；随后，环境根据at确定st中的cet、cgt和cht并计算即时回报rt；最后向智能体反馈st和rt。状态转移过程中的st和rt完全取决于at和st-1，马尔可夫性由式（22）得到保证。

利用该MDP，智能体可逐步优化微网服务商原有的定价策略，从而避免了时间耦合约束对马尔可夫性的破坏，同时很好地保护了用户隐私。

基于所提出的MDP，本研究提出的基于强化学习的求解流程如图2所示。

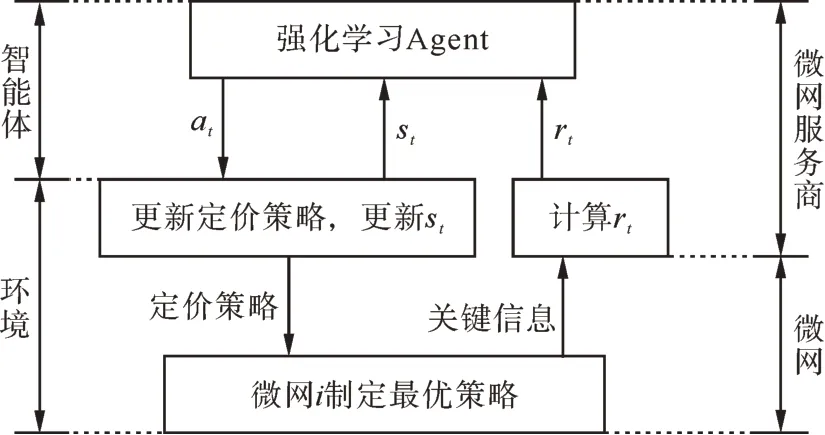
图2 基于强化学习的求解方法示意图Fig.2 Schematic diagram of the RL based solution method

4 算例及分析

本文选取了甘肃省3 个电-气-热微网作为研究对象。图3 展示了微网服务商配备的风电、光伏机组的典型出力曲线，图4 为微网服务商的购能价格，图5展示了3个微网的典型日负荷曲线。

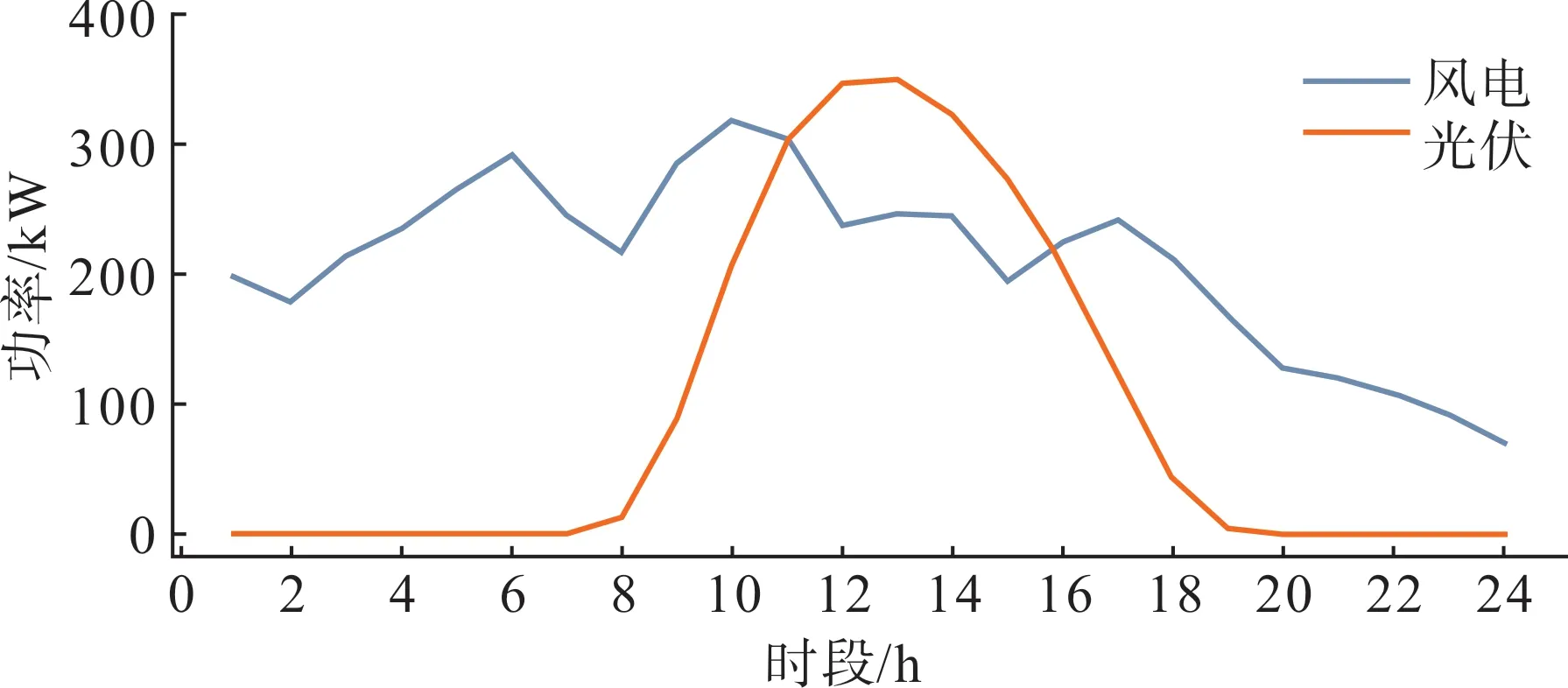
图3 风电、光伏机组的出力曲线Fig.3 Output power curves of wind turbines and photovoltaic units

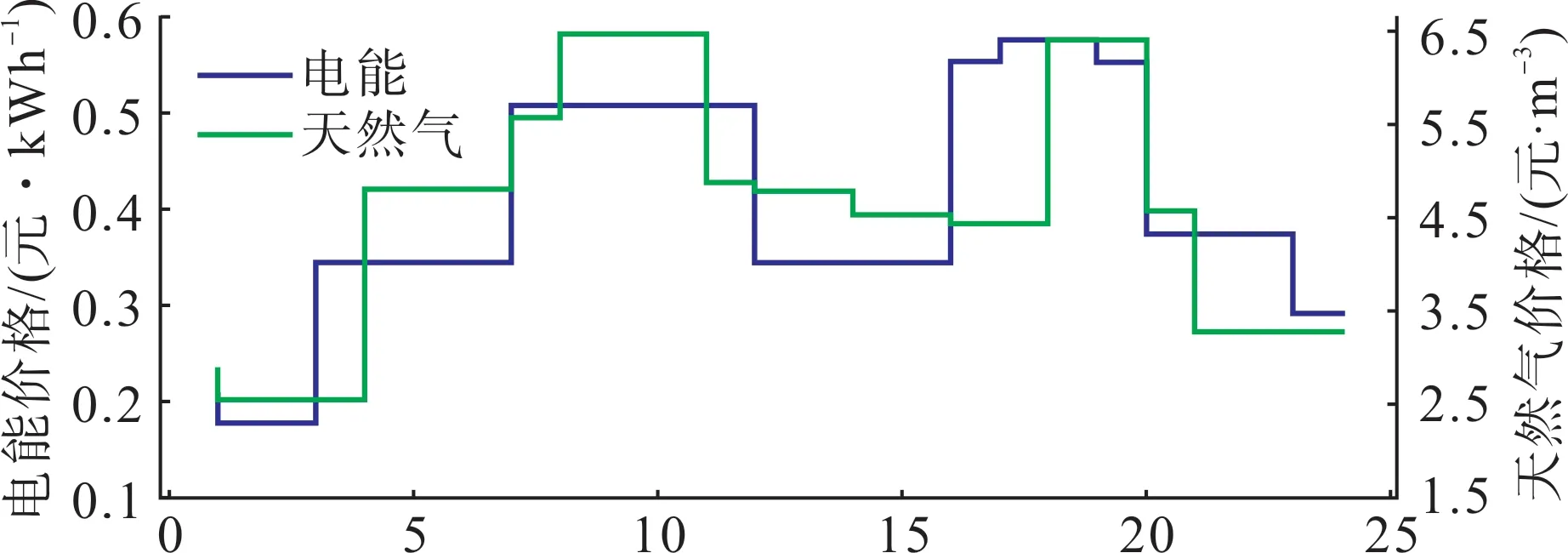
图4 上级能源市场能源价格Fig.4 Energy prices in superior energy market

图5 微网典型日负荷曲线Fig.5 Typical daily load curves of microgrids

电能、天然气的零售价下限等于上级能源市场价格；热能的零售价下限以天然气价格为参照，并考虑一定的制热成本；各类能源的零售价上限设定为下限的2 倍。微网服务商的初始定价方案设定为各类能源的价格下限。

本文选取了鲁棒性强、数据效率高的PPO（proximal policy optimization）算法实现求解。学习率la=4.0×10-4，lc=2.0×10-3；折扣因子γ= 1；梯度裁剪阈值为0.2。

4.1 求解结果

4.1.1 收敛曲线

图6 展示了本算例的收敛曲线，可以看出求解过程在1 165 次左右收敛。左坐标轴表示智能体的总回报，右坐标轴表示各微网目标函数的负值。训练初期不合理的定价策略使各微网削减了更多弹性负荷，这使得服务商的利润较低且微网的需求响应成本较高。随着训练的进行服务商的利润有所提高，更低的需求响应成本也使得微网总成本有所下降。随着定价策略不断优化服务商的利润持续提高，而各微网的总成本也持续增加，图6 中左右轴对应曲线呈现相反的变化趋势，这符合斯塔克尔伯格博弈中领导者与跟随者非合作竞争的利益变化趋势。当达到博弈均衡时智能体的总回报为43 293.99元，初始利润为-1 885.81 元，则微网服务商的实际利润达到41 408.18元，3个微网的总成本分别为43 791.53元、45 718.06元、39 223.76元。

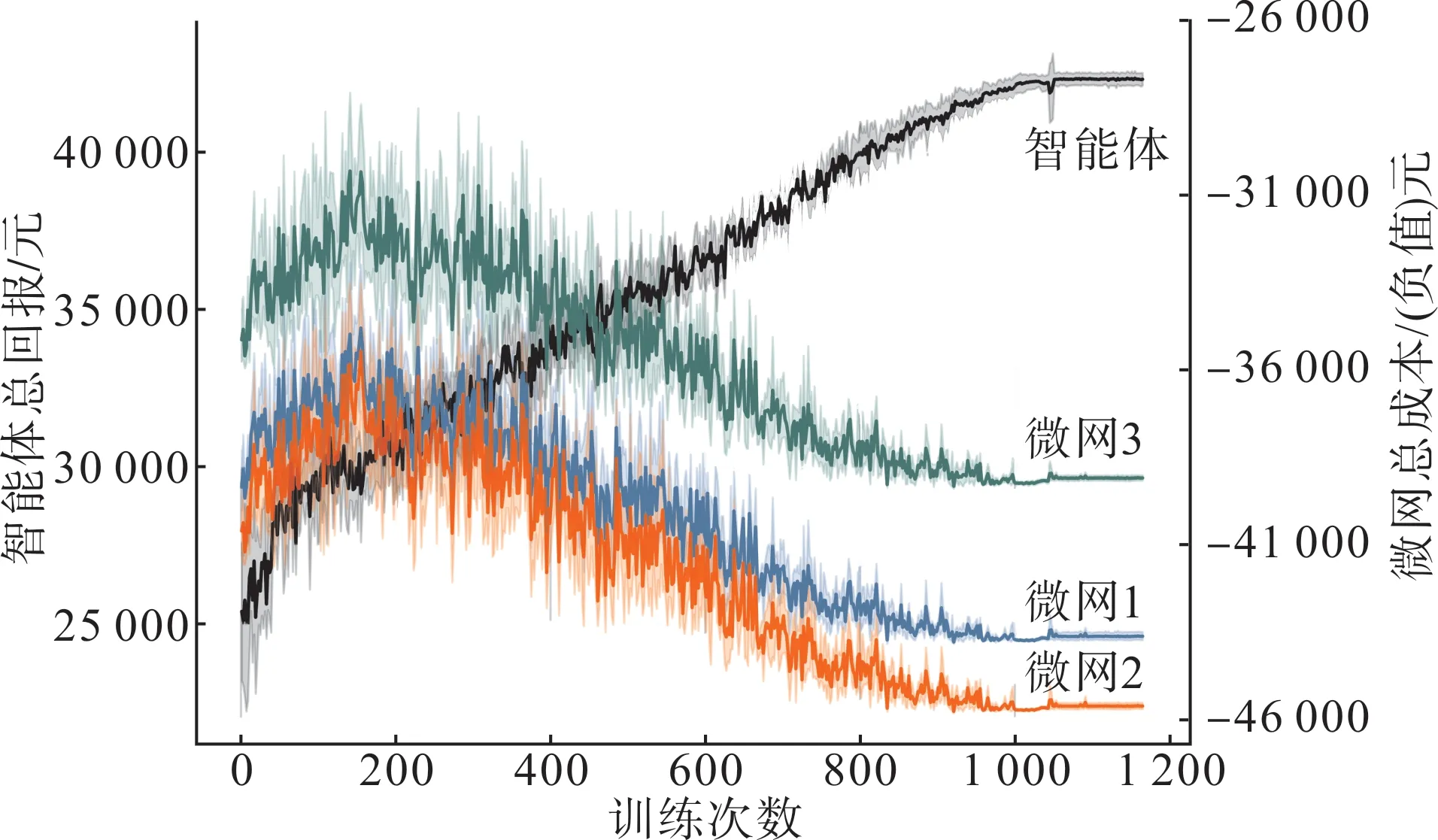
图6 算例收敛曲线Fig.6 Convergence curves of the case

4.1.2 微网服务商及各微网策略

微网服务商的定价策略如图7 所示，智能体的动作值 实际为初始定价方案的倍数。受篇幅限制，图8以微网1为例展示了微网的最优策略。

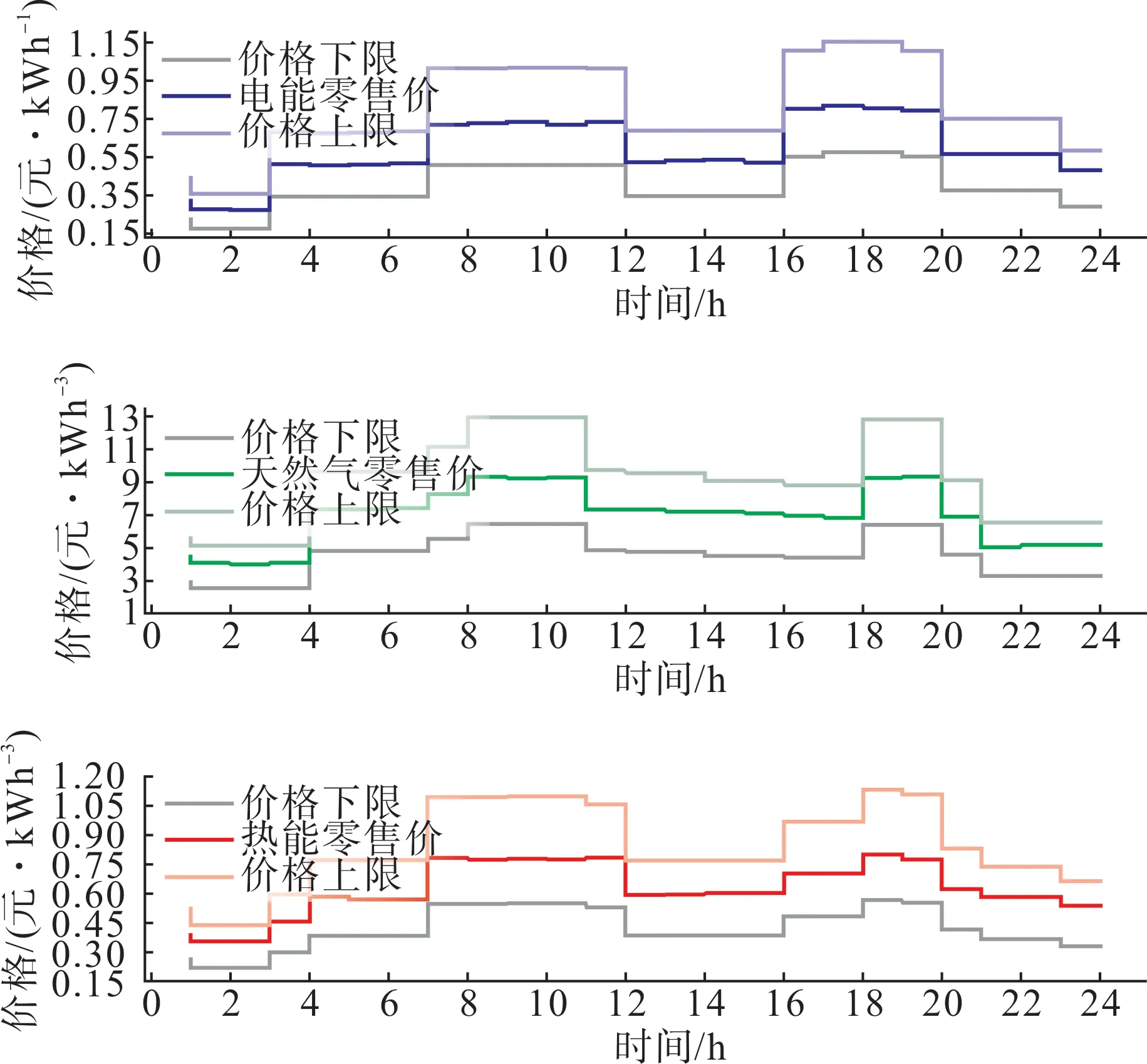
图7 微网聚合商定价策略Fig.7 Pricing strategy of MSP

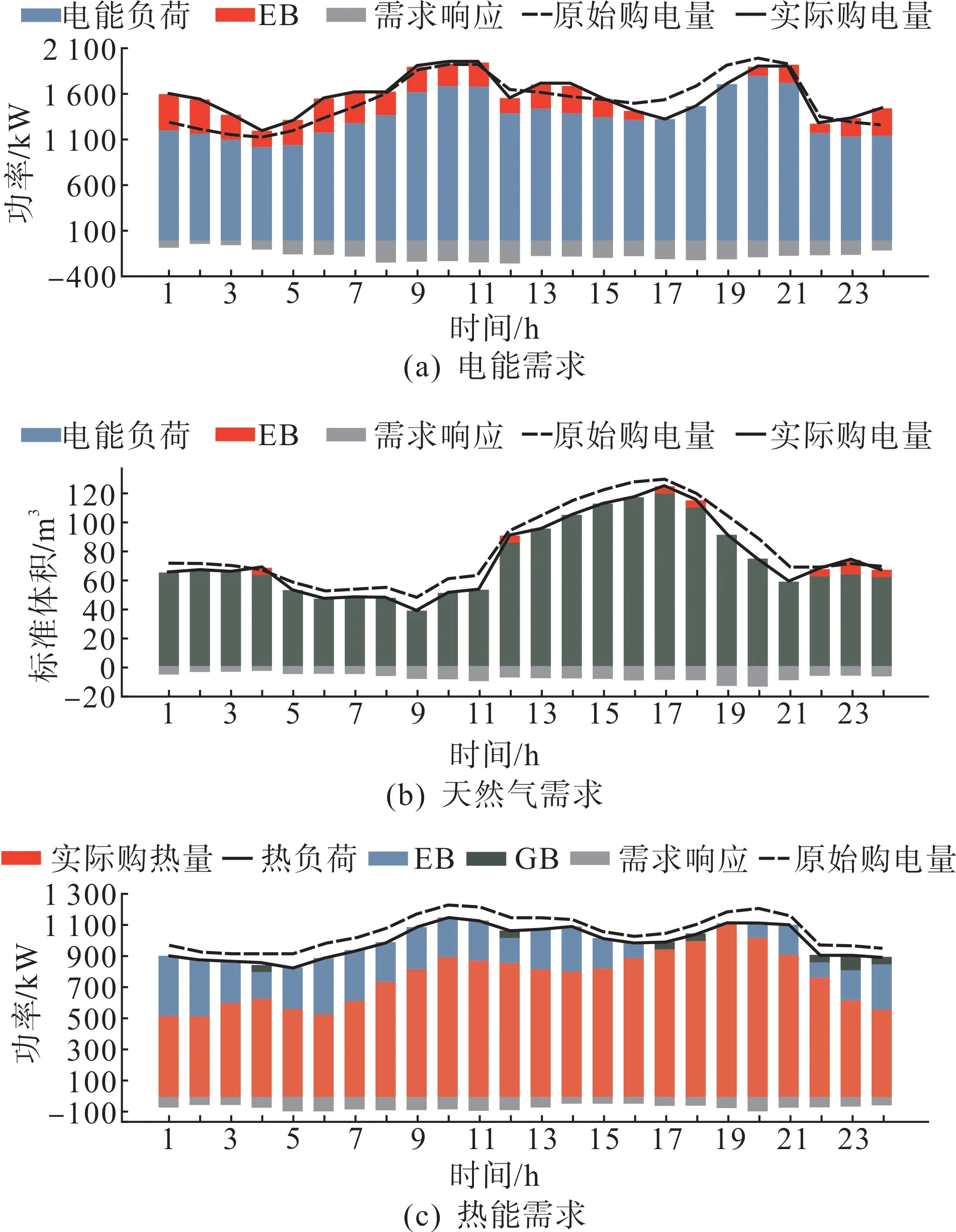
图8 微网1最优策略Fig.8 Optimal strategy of microgrid 1

可以看出，当价格偏高时各微网会削减或平移更多的弹性负荷以减小购能成本，这也会影响微网服务商的利润。因此，为避免相应时段的交易量大幅减少，微网服务商会采取更保守的定价策略。对比各微网的策略可以看出，各微网可通过调整需求响应参数影响博弈结果。另外，当热能零售价过高时各微网也可利用EB、GB降低供热成本。

4.2 求解方法评估

本节选取了不同的随机数和零售价价格区间以验证博弈均衡解的唯一性和所提方法的稳定性。

4.2.1 随机数

PPO 算法受随机数的影响，训练结果可能影响均衡解的结果。图9 以电价结果为例展示了5 组不同随机数对均衡解的影响。不同随机数对交易各方利润或成本的影响不超过0.83%。

图9 随机数对均衡解的影响（以电价为例）Fig.9 Influence of random numbers on the equilibrium solution（e.g.electricity prices）

4.2.2 价格区间

研究不同价格区间，即智能体不同动作空间对结果的影响。图10以电能零售价为例展示了3种价格区间的求解结果。结果表明不同动作空间下本方法的求解结果稳定。

图11 MDP效果对比Fig.11 MDP effect comparison

4.3 MDP效果对比

本文所提MDP 得到的微网服务商总利润约为41 408.18 元。根据现有研究的MDP 微网服务商的利润等于智能体总回报，约为39 525.43 元。由于不满足马尔可夫性，对比方法的收敛结果与本文所提MDP 方案差距达到4.55%。另外，由于环境的不确定性对比方法的训练过程更不稳定。

4.4 计算性能

本节研究了多微网系统中微网数量对计算时间的影响。所有算例在性能相同的计算机上完成求解，计算结果见表1。

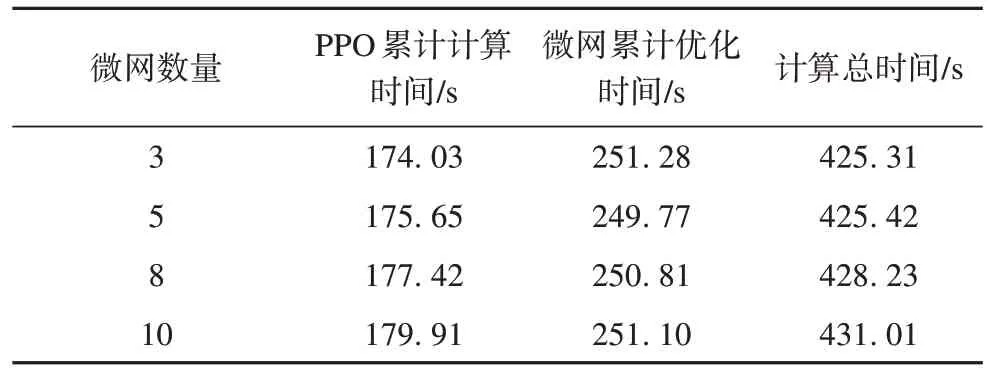
表1 不同微网数量下计算时间Tab.1 Computation time with different numbers of microgrids

本文所提方法展现了良好的计算性能，很好地解决了多微网接入的大规模斯塔克尔伯格博弈问题。由于各微网的优化过程可并行处理，斯塔克尔伯格博弈中跟随者策略的求解受微网数量的影响较小。同时，微网数量的变化对PPO 算法的训练时间没有显著影响，累计训练时间仅略有增加。

5 结语

本文研究了电-气-热多微网系统中微网服务商零售价定价问题。所建立的多微网系统准确描述了微网服务商与各电-气-热微网间的交易模式，所关注的定价问题被描述为斯塔克尔伯格博弈，并被证明存在唯一的博弈均衡点。算例研究表明，所提出的基于强化学习的求解方法能很好地求解存在时间耦合的斯塔克尔伯格博弈。微网服务商采取了恰当的定价方案以提高利润，各微网也能根据特定参数优化自身策略。此外，该方法很好地保护了各微网的隐私并提升了求解效率。