基于时间的关键字路网路径规划

卢航，李艳红，黄金亮

（中南民族大学 计算机科学学院， 武汉 430074）

智能手机等移动设备基本上都具备了GPS 芯片，它们每天都能产生大量的位置信息，轻松地获取用户的位置数据.为了给用户提供基于位置的服务（LBS），产生了大量的LBS 应用，例如，谷歌地图，高德地图等.在日常生活中有很多应用场景，如用户希望找到道路网络上某两个点之间的最短路径.随着用户的需求越来越高，近年来附加了文本信息的空间对象查询，即空间关键字查询［1-4］，受到广泛的关注.每个对象都包含一个或者多个关键字来描述它，当用户需要某个关键字提供的功能时，而具备关键字的目标点往往不是唯一的，因此需要从搜索地点寻找一条最短或者最合适的路径，这样的过程被称为路径规划［5-6］.

然而，现有的研究主要集中在寻找代价最低的路径，例如基于动态权值的路径规划研究等［7-8］.实际上，时间是一个非常重要的影响因素.图1 中，用户位于o点，计划去餐饮店，此时是21：10，根据用户的需求，查询的关键字应为“Restaurant”.如图1 所示，用户o距离包含关键字“Restaurant”的对象v1最近，但v1的营业时间为（15：00-20：30），因此对象v1并不能被选择作为目标点；对象v5虽然距离用户o相较v1更远，但v5此时正在营业，因而应该推荐给该用户从o点到顶点v5的最短路径.为此，将“有效时间”的概念引入路径规划问题中，为每个对象都设置一个有效时间，当查询时间不在对象有效时间内时，具有关键词的对象将不能被推荐.

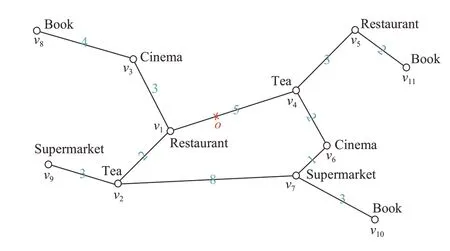
图1 路网图Fig.1 Road network map

为了便于道路网络距离的计算、对象文本信息和时间信息的组织和快速获取，本文在G-Tree［9-10］的基础上改进索引结构，增加时间戳和倒排序列相关信息，将改进后的索引结构称为IGT-Tree.它用GTree 组织路网结构和路网距离信息，用倒排文件组织对象的关键字信息，并为关键字增加有效时间，采用时间戳的方式来存储有效时间.因而可以根据路网距离、关键字信息和有效时间进行剪枝，提高搜索效率.并基于构建的IGT-Tree 设计两种推荐算法，一种是基于时间的目标点查询算法，用于寻找符合有效时间的最近目标点；另一种是在目标点查询算法基础上的路径推荐算法，用在基于时间的道路网络中，为查询点和目标点之间推荐一条最佳路径.简而言之，本文的主要贡献概括如下：

—提出了一种改进G-Tree 的索引结构IGTTree，有效地组织路网结构信息、对象关键字信息和有效时间信息.

—通过模拟实验验证了所提出的基于IGT-Tree算法的目标关键字查询结果和所规划路径的准确率比基于G-Tree的方法更高.

1 准备工作

本节介绍必要的背景信息，以及道路网络上路径规划所采用的数据模型和查询模型.

1.1 路网模型

将道路网络抽象成一个无向加权图G=（V，E），其中V是顶点的集合，E是边的集合，每条边（u，v）∈E连接着两个相邻的顶点u和v（u、v∈V）.并且每条边都关联一个表示距离或者行程时间的非负权重w（u，v）＞0.路径P（v1，vn）=｛v1，v2，…，vn｝（n≥1）是一个有序的顶点集合，即（vi，vi+1）∈E（1≤i≤n-1）.给定顶点u和v，使用δ（u，v）表示从顶点u到v的最短路径，用距离权值dist（u，v）表示δ（u，v）路径上各条边的权重之和.图1显示了道路网络的示意图，如果给定起始点v1和目标点v7，那么δ（v1，v7）=｛v1，v4，v6，v7｝表示v1到v7间的最短路径，其距离权值dist（v1，v7）=9.

1.2 时间范围最佳路径

给定查询起始位置st、目标位置ed 和一组关键字K=｛k1，k2，…，kn｝，其中ki（i∈（1，n））代表各个关键字，道路网络上每个顶点vi（i∈（1，n））都有相应的关键字描述，并且每个顶点v都具有一个有效时间T=［t1，t2］，t1和t2代表时间戳（Timestamp，ts），即一个时间点.例如，［8：30-11：30］代表开始时间戳为8.5，结束时间戳为11.5，在这两个时间戳范围内该关键字是有效关键字.从查询起始点st 到含有符合有效时间t和一组关键字K的目标点ed 的最短路径，称为有效时间的最佳路径（Time-aware Best Path， TBP）.

1.3 数据模型

给定对象o，具有空间位置L=｛l1，l2，…，lm｝（m≥1）和一组关键字K=｛k1，k2，…，kn｝（n≥1），并且每个对象都存在一个有效时间T=［t1，t2］.边（o1，o2）∈E的权值w（o1，o2）表示两个空间相邻对象o1和o2之间的路网距离或者行驶时间，本文假设空间文本对象o位于顶点vi（i∈（1，n））上（表1）.

表1 顶点关键字-有效时间表Tab.1 Vertex keyword-effective timetable

1.4 查询模型

给定道路网G，假定用户位于查询点st，其关键字集合为K=｛k1，k2，…，kn｝（1≤i≤n）.基于上述信息，希望找到一条最佳路径TBP（st，ed，K，t），在查询时间t从起始点st 到符合其有效时间T且含有目标关键字K的结点ed 之间的一条最短路径δ（st，ed），其权值为dist（st，ed）.

2 数据索引IGT-Tree

IGT-Tree用于规划道路网络最佳路径查询的索引技术.G-Tree 和IR2-Tree［11-12］这两个索引启发了通过设计IGT-Tree 来解决TBP（st，ed，K，t）的查询问题.G-Tree 被用于道路网络上的路网距离计算，而IR²-Tree 被用于欧氏空间中的空间关键字查询.虽然这两种索引结构不能直接用于道路网络上最佳路径查询，但可以基于该思想，改进并创建一种新的索引结构IGT-Tree，以满足最佳路径查询的要求.

2.1 IGT-Tree的图划分

以图1 路网为例，使用多级划分算法［13］将路网抽象出的无向图划分成了若干个子图，由于图划分过程是通过多级划分算法来执行的，保证了每个子图大小几乎相同.图2 是IGT-Tree 的图划分例子，整个道路网路被划分为两个子图，分别用G1和G2表示.然后，G1继续被划分为G3和G4两个子图，类似的G2被划分为G5和G6两个子图，直到每个子图的顶点个数小于预设值（一般大于等于2）时停止划分.将两个子图连接起来的顶点称为边界点.图G1由子图G3和G4组成，顶点v1、v2和v3构成了G1的边界点；G1和G2共同组合成了G0，G0的边界点由v1、v2、v4和v7组成.

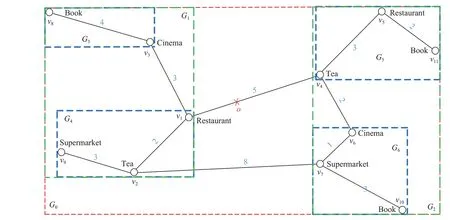
图2 IGT-Tree的路网图划分Fig.2 Road network map division of IGT-Tree

2.2 IGT-Tree的倒排索引

图1中，每个顶点都包含关键字的信息，对IGTTree每个结点通过倒排文件索引该结点覆盖区域内顶点的关键字信息.假定系统有N个关键字，对系统中的所有关键字按顺序排列，每个关键字对应一个序号.IGT-Tree 每个结点设置一个N位的二进制数，以表示该结点是否包含此关键字.对于叶子结点，对于每个关键字，如果该叶结点包含的对象存在该关键字，则对应位置为1，否则为0；对于非叶子节点，将对应孩子结点的倒排序列通过逻辑“或”运算来得到其倒排索引.例如，对于叶子节点G4，它对应的顶点v1、v2和v9所包含的关键字为“Restaurant”、“Tea”和“Supermarket”，这些关键字所对应的倒排序列分别为10000、01000、00010，对它们进行逻辑“或”运算后得到11010，因此叶子结点G4的倒排索引为11010.由此可见，根结点G0的倒排索引通常全为1.关键字索引如表2所示.

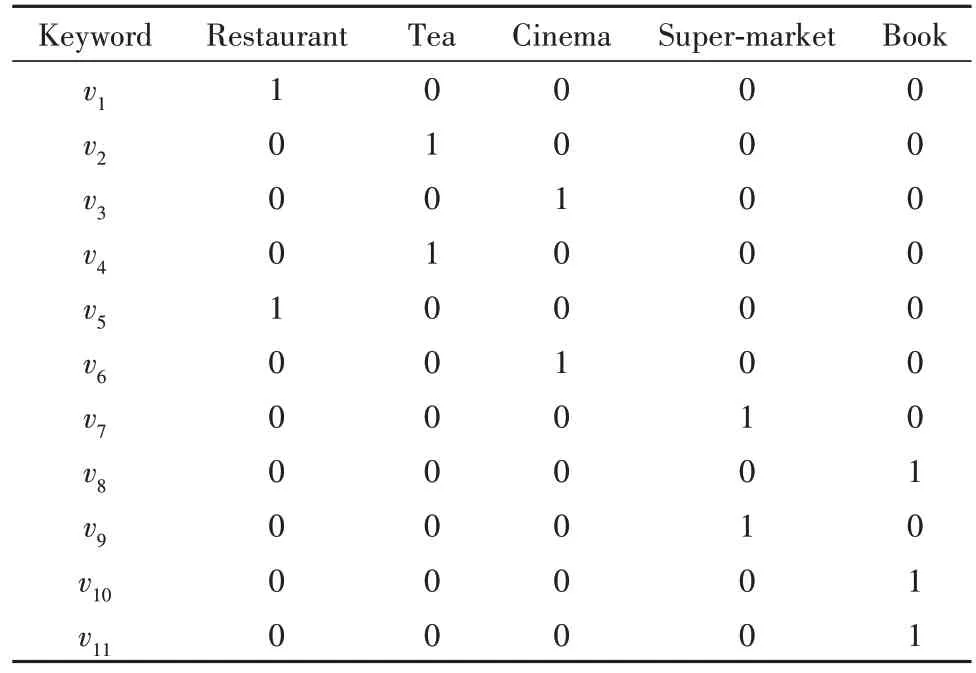
表2 关键字索引Tab.2 Keyword index

2.3 IGT-Tree的距离矩阵

虽然各个结点添加倒排索引，能够快速地区分各个子图是否存在目标关键词，但还是无法知道搜索位置与目标地点的路径距离，因此，计算并保存边界点距离矩阵，便于寻找出顶点之间的最小代价路径.连接两个子图的顶点被标记为边界点，并存储在IGT-Tree 中，边界点距离矩阵保存的是每个子图内部边界点之间的最小权值路径距离.以G0为例，它的边界点是v1、v2、v4和v7，其边界点距离矩阵保存的是各个边界点之间具有最小权重的路径距离，由图3中G0的边界点距离矩阵可知，v1到v2、v4和v7的最小权重路径距离分别为2、5 和9.边界点-顶点距离矩阵保存图的边界点到子图里其他顶点的最小权重路径距离，因此只有叶子结点存在边界点-顶点距离矩阵.表3-6为边界点-顶点距离矩阵.

表3 G3的边界点-顶点距离矩阵Tab.3 G3 boundary point-vertex distance matrix

表4 G4的边界点-顶点距离矩阵Tab.4 G4 boundary point-vertex distance matrix

表5 G5的边界点-顶点距离矩阵Tab.5 G5 boundary point-vertex distance matrix

表6 G6的边界点-顶点距离矩阵Tab.6 G6 boundary point-vertex distance matrix

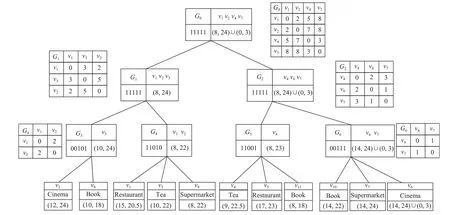
图3 IGT-Tree索引结构Fig.3 The structure of IGT-Tree index

2.4 IGT-Tree索引的有效时间

由于每个顶点所包含的关键字均具有有效时间，为了表示顶点对象的有效时间间隔，引入时间戳的概念，以1 个小时为1 个时间单位，每天都被划分成了24个时间单位，例如（21：00，22：00），可以转化为［21，22］来表示时间段二十一点至二十二点.如表1所示，每个结点都包含了关键词和有效时间的信息.关键字和有效时间保存在IGT-Tree中对应的叶子结点中，对于非叶子结点的有效时间，其处理和倒排索引类似，都使用其子结点的逻辑“或”来计算.例如对于非叶子结点G3来说，其子结点为v3和v8，它们对应的有效时间分别为（12：00，24：00）和（10：00，18：00），将它们转化为时间戳（12，24）∪（10，18），然后通过“或”运算，得到结点G3的时间戳为（10，24）.所以根结点G0的时间戳一般为（0，24）.

2.5 IGT-Tree整体结构

IGT-Tree 结构见图3，对于每个非叶子结点，包含子图的名称、对应的边界点距离矩阵、倒排索引和时间戳；对于每个叶子结点，包含子图名称、对应的倒排索引、边界点-顶点距离矩阵以及时间戳.

3 关键字查询和路网规划

基于所构建的IGT-Tree 索引结构，提出了两种查询处理算法，即有效时间目标点查询算法和有效时间最佳路径规划算法.

3.1 基于有效时间目标关键字查询算法

本算法为用户查找在时间感知路网下包含目标关键字的顶点.算法的主要步骤是寻找包含查询点st 所位于的最小边界矩形（Minimal Bounding Rectangle），即包含st 的叶子结点Gst，再通过它的倒排索引，判断Gst所包含的顶点是否有满足条件的关键字K，如果存在目标点ed′，再查询顶点ed′对应时间戳ted′，从而计算出发点st到目标点ed′所耗费的时间tb=dist（st，ed′）/θ（θ为速度变量，这里取6 km/h）和查询时间t之和得到的预期时间T=t+tb，判断T是否满足结点ed′的有效时间（t1ed，t2ed），若满足，则结点ed′即为目标点ed；若不满足，那么再通过Gst的父结点Gf依次进行查询.

例如，当用户位于道路网络中的顶点v6时，在14：30 时搜索关键词“Restaurant”，此时st=v6，t=14.5，需找到包含关键词K=｛Restaurant｝的目标点ed，同时满足从st 到达ed 时的预期时间T在有效时间（t1ed，t2ed）内.首先将关键词K=｛Restaurant｝转换为其对应的二进制序列，即10000；然后查询IGT-Tree，找到st 所位于的MBR 即叶子结点G6.遍历IGT-Tree可知结点G6的关键字倒排索引KG6为00111，表2 可知结点G6没有关键字K=｛Restaurant｝对应的二进制序列10000，结点G6不符合.然后从G6的父结点G2开始查询，结点G2的倒排索引为11111，存在关键字K对应的二进制序列10000，遍历G2的孩子结点，得到G5包含目标关键字的叶子结点G5.遍历G5包含的顶点，可得顶点v5包含关键词K，计算dist（st，v5）=2，可得T=t+dist（st，v5）/θ=14.83，而顶点v5的有效时间为［17，23］，显然预期时间T不满足v5的有效时间.虽然顶点v5含有目标关键字K，但它不能满足查询要求，故排除掉.再从G2的父节点G0开始查询，通过以上方法可知顶点v1包含关键字K，计算dist（st，v1）=7，得T=t+dist（st，v1）/θ=14.5+1.17=15.67，查询顶点v1的有效时间为［15，20.5］，预期时间T满足v1的有效时间.因此可得查询的目标点ed=v1，如算法1所示.

为了得到包含有效时间的关键字目标点ed，需要从叶子结点Gst开始，通过对包含在叶子结点内的每个节点进行时间戳和倒排序列的剪枝处理，需要对每个非根结点进行一次搜索，时间代价主要集中在对叶子结点Gst、Ged和最近公共父结点Gp之间层数差的遍历操作中，对每层相邻树结点之间都要进行一次最小边界点的计算，而层数差j 的最大值为IGT-Tree 的高度H=logf(V/τ)+1，其中V为顶点总数、τ 为叶子结点包含的顶点数、f为非叶子结点的扇出，因此基于有效时间目标关键字查询算法的时间复杂度为O(logf(V/τ)).

Algorithm 1 Finding the nearest target point ed on IGT-Tree Input： IGT-Tree ， st ， K ，t Output： ed 1： Convert the key K to a binary sequence Kb //将关键字K转化为二进制序列Kb 2： Convert Search time t to timestamp ts //将查询时间转化为时间戳ts 3： Find the leaf node Gst that contains st //找到包含起始点st 的叶子结点Gst 4： while parent node of Gst ！= ∅ do 5： Search the inverted index KGst of Gst //输出结点Gst的倒排索引KGst 6： if KGst contains Kb then 7： Find the vertex ved that contains the keyword K //找到包含关键字K的顶点ved 8： Search the valid time Tved of vertex ved //查询ved的有效时间Tved 9： Calculate t = t + dist（st，ved）/θ 10： if Tved contains t then 11： return ed = ved 12： else 13： Find the Parent node GstP of Gst //找到Gst的父结点GstP 14： continue 15： end if 16： else 17： Find the Parent node GstP of Gst //找到Gst的父结点GstP 18： continue 19： end if 20： end while

3.2 基于有效时间最佳路径规划算法

由上述3.1 可知，当用户位于结点v6，搜索关键字为“Restaurant”即K=｛Restaurant｝，此时查询时间为14：30 即T=14.5 时，符合条件的最近目标点ed=v1，因此δ（v6，v1）=（v6，v4，v1）即TBP=（v6，v4，v1），如何找到TBP中的每个顶点，是本节要解决的问题.

第一步判断起始点st 和目标点ed 是否被包含在同一叶子结点内，由IGT-Tree 可知，包含起始点v6的结点为G6，而包含目标点v1的结点为G4，它们不在相同的叶子结点内；若它们包含在同一叶子结点内，可由该叶子结点的边界点-顶点距离矩阵直接得出最短路径.接下来根据包含顶点v6和v1的叶子结点G6和G4，遍历IGT-Tree 找到最近的公共父结点Gf即G0，查询G6和G4的边界点矩阵分别找到它们的边界点BG6和BG4（BG代表图G中的任意的边界点），计算dist（v6，BG6）和dist（v1，BG4）找到权值最小的边界点Bv6=v6和Bv1=v1（Bv代表顶点v为边界点）；若边界点不为目标点ed，则将Bed作为中间点.由G0的边界点距离矩阵可知，G0的边界点为v1、v2、v4和v7，且位于G0不同孩子结点的最小权值为dist（v1，v4）=5.判断Bv6和Bv1是否为G0的边界点，显然Bv1=BG0=v1，而Bv6≠BG0不为G0的边界点，比较出dist（v6，BG0）的最小权值的边界点v7.虽然到起始点v6权值最小的边界点为v7，但不能直接将v7作为中间节点，需要比较起始点v6到G0中距目标点v1权值最小的边界点v4，即dist（v6，v4）+ dist（v4，v1）=7，和dist（v6，v7）+dist（v7，v1）=11，选择权值更小的为中间点，故将v4作为中间点，根据G0的边界点距离矩阵，可得δ（v4，v1）=｛v4，v1｝；若目标点ed不为G0的边界点，则计算dist（ed，BG0）选择权值最小的边界点作为中间点.因此最终dist（st，ed）=dist（v6，v4）+dist（v4，v1）=7，而δ（st，ed）=｛v6，v4，v1｝，即TBP（v6，v1，｛restaurant｝）=｛v6，v4，v1｝.如算法2所示.

为了寻找起始位置st 和目标位置ed 间的最佳路径，需要对节点st和ed分别位于的叶子结点Gst和Ged寻找最近非空父结点进行查询，对于被查询的结点，需要对其包含的i个满足关键字条件的对象，计算一次有效时间的匹配性，而i不大于τ。同时最多遍历n个树结点，因此基于有效时间最佳路径规划算法的时间复杂度为O(n·τ).

Algorithm 2 Finding the best path from st to ed on IGT-Tree Input：IGT-Tree，st，ed Output：δ（st，ed）1： Find the leaf node Gst that contains st //找到包含起始点st 的叶子结点Gst 2： Find the leaf node Ged that contains ed //找到包含目标点ed 的叶子结点Ged 3： while nearest parent node Gf of Gst and Ged ！= ∅ do //Gst和Ged的最近父结点Gf不为空4： Search the boundary point distance matrix of Gst to get the boundary point BGst //找到叶子结点Gst的边界点BGst 5： Search the boundary point distance matrix of Ged to get the boundary point BGed 6： if st = BGst then 7： if ed = BGed then 8： Search the boundary point distance matrix of Gf to get δ（st，ed） //由Gf的边界点距离矩阵可得δ（st，ed）9： return δ（st，ed）10： else 11： Find the boundary point Bed of the minimum value of dist（ed，BGed） //找到边界点BGed距离ed最近的那个Bed 12： Search the boundary point distance matrix of Gf to get δ（st，Bed）13： return δ（st，ed） = δ（st，Bed）+δ（Bed，ed）14： end if 15： else 16： Find the boundary point Bst of the minimum value of dist（st，BGst）17： if ed = BGed then 18： Search the boundary point distance matrix of Gf to get δ（Bst，ed）19： return δ（st，ed） = δ（st，Bst）+δ（Bst，ed）20： else 21： Find the boundary point Bed of the minimum value of dist（ed，BGed）22： Search the boundary point distance matrix of Gf to get δ（Bed，ed）23： return δ（st，ed）=δ（st，Bst）+δ（Bst+Bed）+δ（Bed，ed）24： end if 25： end if 26： end while

4 实验

采用了两个合成的数据集CA 和SF（通过真实的California和San Francisco两个城市的路网数据和实验系统产生的数据对象合成的），其中随机产生的对象包含了关键字信息、有效时间信息和位置信息.其中CA 包含1458 个数据对象和46 个关键字，SF 包含10000 个数据对象和215 个关键字，对于CA中的每一个对象，通过zipf分布［14］为其分配1-2个关键字，每个对象的有效时间范围设置在［0-24］，且遵循高斯分布［15］；对于SF 中的每一个对象同样采用zipf 分布的方式为其分配3 个关键字.现实生活中，每个对象能具备多个关键字，SF 和CA 的对象的有效时间设置方式相同.另外，每个对象的位置都随机分布在路网的节点上，由于以上的数据集是根据数据对象的时间特征和关键字特征进行合成的，因此对实验结果没有影响.表7为两个数据集的特征.

表7 实验数据集特征Tab.7 Characteristices of data sets

4.1 系统设置

设备为Intel Core i5-8400，2.8 GHz CPU，GTX 1060TI，16 GB RAM Windows10 的电脑，所有算法的开发及运行均在Java 1.8.0_302的运行环境下完成.

4.2 实验结果分析

4.2.1 索引建立性能分析

本节评估IGT-Tree索引的构建时间和内存空间消耗这两方面的性能.图4（a）显示在CA 和SF 两个大小不同的数据集下，IGT-Tree 和G-Tree 索引建立耗费的时间和占内存空间的大小.尽管IGT-Tree 索引加入了有效时间，其创建时间和G-Tree 相差无几；不过随着数据集的增大，它们两者的索引创建时间差距会稍微增大.图4（b）显示IGT-Tree 索引所占内存空间大小略大于G-Tree 索引，这是因为IGTTree 索引相较于G-Tree 中除了边界点距离矩阵、倒排索引和边界点-顶点距离矩阵以外，每个结点和叶子结点所包含的顶点还包含了时间戳的内容.

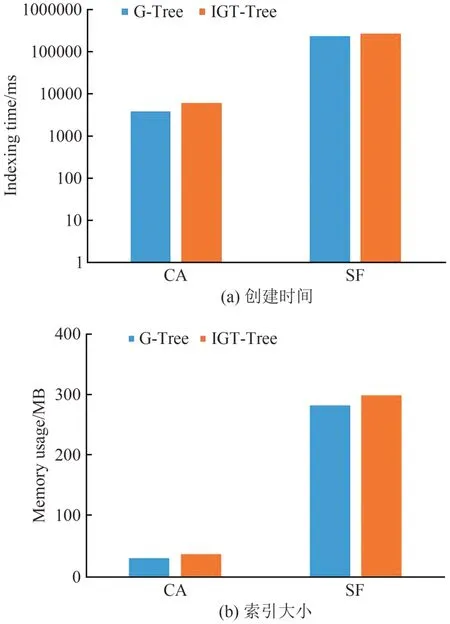
图4 IGT-Tree和G-Tree的索引创建时间与大小Fig.4 Index creation time and size of IGT-Tree and G-Tree

4.2.2 关键字查询分析

根据CA 和SF 两个数据集，设置不同的关键字数，CA 设置为1 个，SF 设置为2～3 个，设置每个对象的有效时间T 随机分布在［0-24］内，查询G-Tree 和IGT-Tree两种索引结构下查询算法对于目标关键字查询的正确率.图5（a）显示IGT-Tree 的查询时间比G-Tree 稍大，图5（b）中，在关键字K更大的SF 数据集里，查询时间变长但正确率会随之变大，当数据集变大后，IGT-Tree 和G-Tree 的查询正确率也变得比较接近，并且正确率同时都在提高.因为随着单个对象包含的关键字数增多，在有效时间不变的情况下，有效的目标对象会随之增多，因此增大了查询的正确率，并且在G-Tree 下查询的关键字，由于可选的对象增多，在查询时，目标对象处于有效时间的可能性同时变大，因此随着K的数值变大，G-Tree的查询正确率会逐渐接近IGT-Tree.

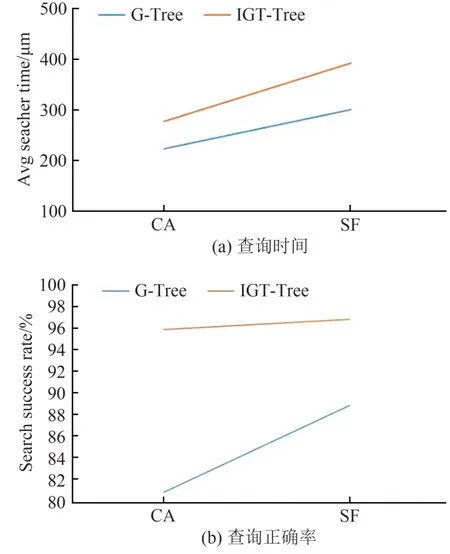
图5 IGT-Tree和G-Tree关键字查询时间与正确率Fig.5 IGT-Tree and G-Tree keyword query time and accuracy rate

4.2.3 不同时间段查询的准确率分析

为了探究在一天内各个不同时间点查询目标的正确率，G-Tree和IGT-Tree两者的性能差别，根据CA 和SF 两个数据集，设置不同的关键字数，CA 设置为1 个，SF 设置为2-3 个，设置每个对象的有效时间T 随机分布在［0-24］内，对比G-Tree 和IGT-Tree两种索引下查询算法在不同时间内目标关键字的查询正确率.根据图6，结果显示随着数据集变大，两者查询的正确率都随之提高.在［8，16］这个时间区间内，IGT-Tree 和G-Tree 查询的正确率差值收小并且变化规律类似，但在［20，24］∪［0，8］这个时间区间内，IGT-Tree 的查询正确率相较于G-Tree 提升明显，随着数据集的增大，两者之间的正确率的差距也有所缩小.因为查询时间越晚，处于有效时间的对象数量也在减少.G-Tree 的查询对象往往都是时间代价最小的，但随着T处于［20，24］∪［0，8］这个时间区间内，很多对象已经不在有效时间范围内，这也导致IGT-Tree查询正确率的降低.

图6 不同时间点查询准确率对比Fig.6 Comparison of query accuracy at different time points

5 结论

为解决基于时间的关键字路网路径规划问题，本文提出一种有效的路网索引结构IGT-Tree，并在此基础上提出关键字查询算法和路径规划算法.对比以往的索引结构G-Tree，在有效时间的路网关键字查询下，能提高查询的准确率，尤其是在T=［20，24］∪［0，8］这个时间段内，查询准确率相较于G-Tree提升明显.实验结果验证了本文提出的IGT-Tree 索引结构和算法在处理基于时间的路网关键字查询和路径规划的可行性和准确性.