基于PCA-FSEM方法的风力发电机可靠性研究
郑玉巧, 郎启发, 施成龙, 刘宇航, 刘燕杰
(兰州理工大学 机电工程学院, 甘肃 兰州 730050)
风力发电机为结构层次复杂、零部件众多的复杂机电系统,其工作环境多位于偏远地带,易遭遇暴风雨、雷电、结冰等极端天气.此外,随着近年来风力发电机逐渐复杂巨大化,并且风场向环境更加恶劣的地域拓展,导致风力发电机故障频发,风力发电机的稳定运行面临着严峻挑战.风力发电机的部件材料强度、制造工艺和安装过程均要求较高,进行维护时通常还需要动用大型工程设备,运行维护成本高、难度大.国家标准规定,并网型陆地风力发电机的设计寿命为20年,年可利用率需达到97%以上[1].据统计[2-3],由风力发电机可靠性问题带来的风电场年运行维护成本约占总投资的1.25%~6%,维护备件费用约占总投资的50%~60%[4],这给风电场经济效益带来巨大损失.因此,研究风力发电机可靠性问题显得尤为关键.
风力发电机的不断发展促使运行数据可靠性建模和统计的研究不断完善.然而,基于运行数据的可靠性评估方法缺少相关深入分析,目前运行数据的建模依据不统一,并且充满了主观经验色彩,造成可靠性评估结果可信度不高.况且可靠性建模和运行数据的统计分析是可靠性评估的核心问题.鉴于此,本研究依据某风场风力发电机的运行数据,利用统计多变量分析中主成分分析(principal component analysis,PCA)法和模糊理论,建立风力发电机可靠性评价模型,对保证风力发电机稳定运行和降低风场运行维护成本具有重要意义.
1 基本理论简介
1.1 风力发电机可靠性模糊评价模型
风力发电机在运行过程中,评价标准主要通过多指标综合评判,评价具有一定的模糊性.因此,采用基于模糊理论的模糊评价模型(fuzzy synthetic evaluation model,FSEM)对风力发电机关键可靠性指标进行评价是可行的.
基于PCA的风力发电机可靠性模糊评价模型建立步骤如下[5]:
1) 确定评价指标
选取评价指标体系U={u1,u2,u3,…,um}建立风力发电机m种可靠性评价初始矩阵q,V={v1,v2,v3,…,vn}为刻画每个指标所处的各评价等级.本研究风力发电机可靠性指标采用五级评判,分别是优秀、良好、一般、较差、非常差,即V={v优秀,v良好,v一般,v较差,v非常差}.不同可靠性评价指标之间采用理想解法(TOPSIS)进行量纲标准化,将数据标准化在0~1之间[6],计算方法为
(1)
式中:qij表示从指标ui出发评价等级为vj的隶属度,且0 2) 构造评价矩阵确定权重 从指标ui(i=1,2,…,m)入手,对指标集中单个评价指标做单指标因素评判.风力发电机对评价qi=[qi1qi2…qin]在等级vj(j=1,2,…,n)的隶属度为qij,整理可得第i个指标的单指标评价集合[7-10].那么,由m个指标的评价子集可得总评价矩阵Q.每个评价对象从U到V的模糊关系Q可表示为隶属度函数矩阵,即 (2) 3) 进行模糊合成 Q的行表示风力发电机各可靠性评价指标对各级模糊子集的隶属程度.用模糊权重向量A将不同的行进行综合,可得风力发电机总体对各级模糊子集的隶属程度,即模糊综合评价向量.引入V中模糊向量B,称之为模糊评价,即决策集,计算式为 B=A·Q (3) 各可靠性评价指标具体反映其在相应的可靠性特征方面分布状态.为充分利用B携带的信息,将各等级评价参数与评价结果综合考虑,使其可靠性评价结果更加符合实际. 权值计算是模糊评价的关键.权值大小表示各可靠性指标对风力发电机评价结果的影响程度,大多数情况由专家经验法确定.但专家经验法受知识、经验等因素的制约,对最终可靠性评估结果影响较大.同时,由于专家经验法具有主观性,所以对风力发电机可靠性的客观评价有一定局限性. 为减少确定权值存在主观性,使风力发电机的模糊评价模型结果更可靠,将对可靠性指标不敏感的熵权与专家经验法权重结合,构造复合权重[11-12].该方法在根据数据差异赋权的同时兼顾专家经验,各指标权值与指标差异密切关联,避免其他因素干扰.熵权虽能区分指标的差异性,但对指标的重要程度不敏感,反映不准确,而结合专家经验法恰能完善这一局限性.计算过程如下: 1) 计算熵权 设风力发电机有多种可靠性状态,每个可靠性状态概率为p.对于m个评价状态n个评价指标的风力发电机,第i个指标熵权为 (4) 对应的熵权为 (5) 对应熵权向量为 FH=[FH1FH2…FHn] (6) 构造复合权重向量F=[F1F2…Fn].其中, (7) 式中:FE=[Fe1Fe2…Fen]为专家经验法所得权重,是根据专家经验打分计算所得的权重比. 由此可得熵权与专家经验法权重结合构造的复合权重,即模糊权重向量A: (8) 根据式(8)的计算结果,结合式(3)可得单因素模糊评价集. 2) 计算评价矩阵 将单因素评价集与复合向量合成,得到新的评价向量C,即 (9) 式中:Fi为平均加权算子. 可靠性评价规程(试行)将风力发电机运行状态划分为可用(A)、不可用(U).其中,可用分为运行(S)和备用(R),不可用分为计划停运(PO)非计划停运(UO)[13].备用状态下设备分为调度停运设备(DR)和受累停运设备(PR).受累停运设备有场内原因受累停运设备(PRI)和场外原因受累停运设备(PRO). 风力发电机故障停运包括计划停运和非计划停运.其中,计划停运指机组处于检修或维护状态,非计划停运指机组处于不可用状态,但不是计划停运状态.对于机组这个复杂系统,本研究将可靠性指标分组进行主成分分析,选取关键可靠性指标,结合模糊评价建立评估模型. 主成分分析法是利用降维的思想,在损失少量信息的前提下,把多个指标转化为几个综合指标的多元系统分析方法.主成分分析法可将风力发电机可靠性评价指标中多个指标通过多维坐标变化转化为少数几个互不相关的综合变量,从而达到降维效果.该方法的使用目的是将多维可靠性评价指标通过线性变化投影到低维空间,以此找出代表原始数据绝大多数信息的投影方法.在本研究过程中,将统计期内相关性强的风力发电机各指标分组,并做主成分提取.其中,风力发电机A01、A02、B03各评价指标主成分分析解释如图1所示. 图1 主成分分析Fig.1 Principal component analysis 图1可用于辅助判断主成分提取个数,当折线由陡峭突然变得平稳时,陡峭到平稳对应的主成分个数为参考提取主成分个数.结合主成分与研究项对应关系的情况,综合权衡判断得出主成分个数.并且所有样本点在坐标轴上的值等于主成分对应的特征值.主成分分析可消除数据之间的相关性和冗余度.具体步骤如下[14]: 1) 确定所要分析的变量,收集相关数据; 2) 对收集到的初始数据进行标准化处理,消除不同量纲之间的影响,可得相关系数矩阵R,即 (10) 式中:rij为原来变量Xi和Xj的相关系数. 3) 根据Rαi=λiαi计算R的特征值和特征向量,其中,λi为系数矩阵R的特征值,αi为特征值对应的特征向量; 4) 计算分贡献率和主贡献率; 5) 计算主成分载荷lij,即 式中:主成分载荷p(Zi,Xj)为主成分Zi与原始指标Xj的相关系数;ei,j为主成分与原始指标的相关方向指数,方向一致取1,否则取-1;λr为主成分Zi对应的特征值; 6) 确定主成分数量,选择λi大于1所对应的成分作为提取分析的主成分,或按照累计贡献率达到的百分比确定,一般情况下取累计贡献率为80%以上的P个成分作为主成分; 7) 计算各主成分得分. 本研究选取可利用率、运行系数、有效性、计划停运系数、平均无故障可用时间和暴露率等多个可靠性指标[15].选取2组风力发电机通过各可靠性评价指标之间相关性分析将其分组. 对各指标进行主成分分析时,通过进行KMO值分析和Bartlett检验对应p值,判断其是否适合进行主成分分析[16-18].若KMO值大于0.6或p值小于0.05,说明可进行主成分分析.初始数据分析得KMO值为0.487,p值为0;主成分分析后剔除年计划停机次数和非计划停运次数的KMO值为0.617,p值为0.由此说明,主成分分析效果更佳.因此,本研究将剔除这2项指标参数.分组情况如表1所列. 表1 风力发电机可靠性指标分组情况 取该风场A01~A10和B01~B15共25台风力发电机的可靠性指标作主成分分析.根据Rαi=λiαi,求解主成分特征值.最大特征值所对应的投影方差最大,特征向量所对应的线性变换Fi为线性变换数据信息最多的成分.提取特征值分别为3.903、2.724、1.255且累积方差贡献率为87.585%的3个主成分,综合表述风力发电机的可靠性信息.主成分分析结果如表2所列. 表2 主成分分析结果 根据主成分分析可得分系数矩阵,结合各可靠性指标与主成分载荷系数选取关键的可靠性指标.PCA法分析载荷系数结果如表3所列. 表3 载荷系数结果 根据成分可得分系数矩阵,建立主成分与研究项之间的关系等式,即 F1=0.106·α+0.060·β+0.185·SF+0.225·EXR-0.122·POF-0.213·UOF-0.222·UOR+0.162·MTBF+0.144·CAH F2=0.279·α+0.077·β+0.232·SF-0.134·EXR-0.279·POF+0.196·UOF+0.175·UOR+0.168·MTBF-0.192·CAH F3=-0.126·α+0.732·β-0.1236·SF+0.211· 综合主成分得分是方差解释率(概括性评价指标)与成分得分乘积的累加,本研究数据计算表示为 通过载荷系数矩阵中每个主成分与可靠性指标之间的对应关系,展示主成分对所研究可靠性指标信息的提取情况.由表3可以看出,所有系数绝对值均大于零,意味着可靠性指标与主成分之间关联性较强.载荷系数大于0.4时,主成分对可靠性指标信息提取良好,即主成分提取信息量是可靠性指标主要部分.鉴于此,风力发电机关键可靠性指标被提取出来,分别为运行系数、非计划停运系数、非计划停运率、平均连续可用时间、平均无故障可用时间、可利用率、计划停运系数. 根据PCA法分析结果,对风力发电机可靠性关键评价指标进行选取,提取可靠性指标主成分分析中与主成分1之间载荷系数绝对值大于0.5的关键可靠性指标. 除了平均无故障可用时间和运行系数之外,考虑到风力发电机实际运行情况和主成分分析结果,将风力发电机的平均连续可用时间、暴露率、非计划停运系数和非计划停用率作为机组可靠性评价指标,进行可靠性模糊模型评价,即建立评价指标体系,表达式为 U={MTBF,SF,CAH,EXR,UOF,UOR} (12) 从2组风力发电机A01~A10和B01~B15中各选取5台,将10台风力发电机可靠性指标运行统计数据作为分析参考数据.根据指标计算规则计算可靠性指标,数据如表4所列. 表4 风场10台风力发电机运行可靠性指标数据 根据表4中可靠性指标运行数据,推导指标评价矩阵,即 对上述指标利用式(3)进行标准化,可得标准评价矩阵 根据专家经验法,风力发电机最终可靠性5个等级评价结果如表5所列. 表5 可靠性指标临界值 根据表5中数据和式(4)可得单设备可靠性指标隶属度函数矩阵为 由专家经验法和风力发电机实际运行状态可得专家权重向量为FE=[0.05 0.1 0.2 0.2 0.25 0.2]. 根据式(4~6)计算对应熵权向量为FH=[0.157 6 0.194 9 0.153 6 0.176 1 0.165 9 0.184 1]. 根据式(7)计算复合权重为F=[0.046 7 0.097 8 0.182 2 0.208 9 0.246 0 0.218 4]. 采用加权算子求解各风力发电机评价向量,按最大隶属度原则对所选机组的可靠性进行评价,结果如表6所示. 表6 风力发电机可靠性评价结果 本研究采用PCA法消除风力发电机可靠性评价指标之间的冗余度和相关性,提取部分关键可靠性评价指标,主成分特征值分别为3.903、2.272、1.255,累积方差贡献率为87.585%.由此说明,所提取主成分可综合表示风力发电机的可靠性信息.选取研究的机组处于相同风场,运行外部环境一致,内部结构相同.由此可知,机组可靠性越高,发电量、运行率越高.用单一可靠性指标评价机组可靠性时发现:B02单机运行率高达98%,但其实际总发电量却最低;A04单机运行率最低,但发电量却较高.由此表明,单一可靠性指标评价时存在误差.A05、B03单机各项指标均高,实际运行状态良好,发电量高,表明其综合可靠性更高,与研究结果一致.因此,PCA法对定量评估机组可靠性具有指导意义.

1.2 模糊模型评价指标权重计算

2 风力发电机可靠性指标
2.1 可靠性指标分析
2.2 主成分分析法

2.3 风力发电机可靠性指标主成分分析


2.4 基于PCA法选取风力发电机可靠性关键指标

EXR+0.060·POF-0.051·UOF-0.047·
UOR-0.050·MTBF-0.417·CAH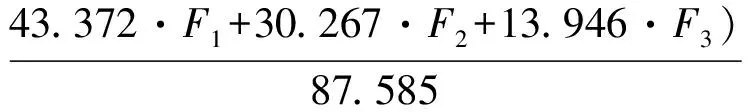
3 模糊模型评价



4 结论

