一种新型调节阀结构介绍及流场分析

张旭阳，张鲲羽,2，李一兴

（1.上海船舶设备研究所，上海 200031 2.上海交通大学机械与动力工程学院，上海 200240）

0 引 言

调节阀是汽轮机通流结构中的重要组成部分。在汽轮机运行过程中，调节阀通过阀头的提升与下降，控制着汽轮机的蒸汽流量，进而对汽轮机的转速及做功能力进行控制。由于调节阀内部结构流动状态复杂，会造成一定的压力损失。而工作蒸汽在进入通流结构前必须经过调节阀，因此调节阀的经济性直接影响整个汽轮机的经济性。韩中合等[1]在研究中提出调节阀压力损失每增加1%将导致汽轮机效率下降0.4%。

经过调节阀的流体将产生复杂而且强烈的旋转流动。压力损失是由于调节阀喉部产生的节流损失、阀头表面的边界层分离、阀座下方的“空穴”区及肾型涡的综合作用产生的，上述影响使得调节阀下游区域充满了强烈的旋涡，形成较大的压力损失[2]。

郑国等[3]对300MW汽轮发电机组空心阀头结构进行计算分析，其研究结果表明阀壳内壁中存在的裂纹、凹坑以及调节阀内部不光顺的流道设计使得调节阀后气流产生了强烈的不稳定性，通过优化阀壳内型腔线使得调节阀内流动更为光顺，机组的安全经济性得到了一定的提高。舒相挺[4]等在研究中发现，调节阀在较小开度时阀门内部的流动紊乱程度较高，流体流动导致的调节阀内部振动可能使得调节阀内部产生较为强烈的共振现象，使得调节阀的安全性与经济性受到较大的威胁。杨宗鑫等[5]针对球形阀头调节阀在一定开度下流动损失较大的问题，提出了一种新型滤网设计，小开度下滤网后流场结构的稳定性与通流特性使得调节阀的全压损失系数降低，阀门通流性能显著改善。李明强[6]则通过优化汽轮机的配汽方式进行优化改造，在各工况下各阀均处于较大开度的状态下阀门的节流损失大幅降低，达到提高机组在部分负荷运行经济性的目的。相晓伟[7]在针对实心阀头的结构优化中提出在阀腔内增加导流筋结构以消除阀头下方的空穴区，减少调节阀内部回流，但是该结构的增加并未使得流动情况得到有效改善。肖鑫等[8]对带有空心阀头的调节阀的扩压角、空心阀头型线及偏心度进行设计优化，并通过计算得到最佳的扩压角、空心阀头外形轮廓及偏心距，使得阀腔内的压力损失达到最小。周刘中[9]则尝试对阀笼窗口进行异性加工，使得调节阀在较小流量下能够保持较大的调节灵敏度，增加系统平稳性，阀内流动状态得到改善。李一兴[10]等通过对锥形实心阀头和空心阀头的结构分析，提出了带有导流锥的空心阀头结构，使得汽轮机调节阀在较小开度下的流动状态得到改善。

本文以某型汽轮机的空心阀头作为研究对象，对其流动结构进行分析，并根据分析结果提出了一种余弦阀头结构。研究结果表明，采用余弦阀头后，调节阀内的涡结构发生了明显变化，涡强度发生了明显的下降，调节阀的全压损失也随之下降。

1 模型与网格介绍

某汽轮机调节阀结构采用轴向进汽(x轴)、径向出气(y轴)，如图 1所示。流体从入口面进入环形的阀腔后通过阀头与阀座之间的喉部区域进入阀座内的流出通道并最终流出阀门。通过提升阀头，增大阀头与阀座之间喉部区域的面积能够调整调节阀通过的流量。

图1中给出了调节阀内部的流线及调节阀入口面与出口面的位置。其中入口设置为质量流量入口，出口设置为压力出口，阀杆、阀头、阀座及阀腔内表面均设置为无滑移绝热壁面。各出入口边界条件如表 1所示。

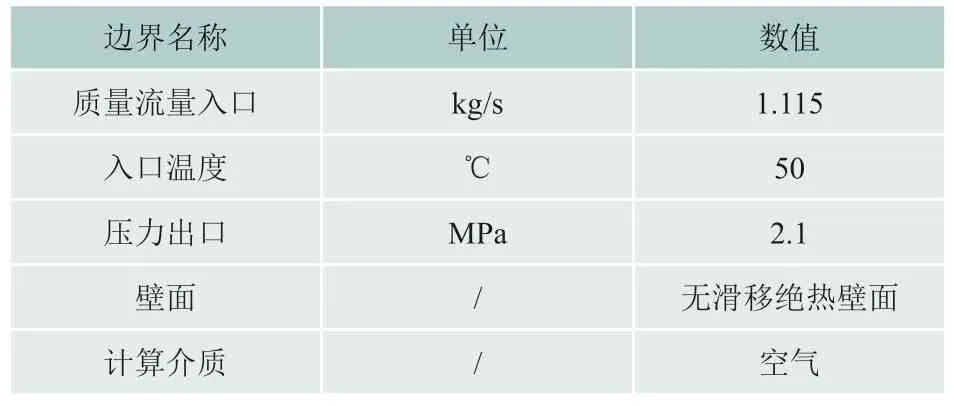
表1 边界条件

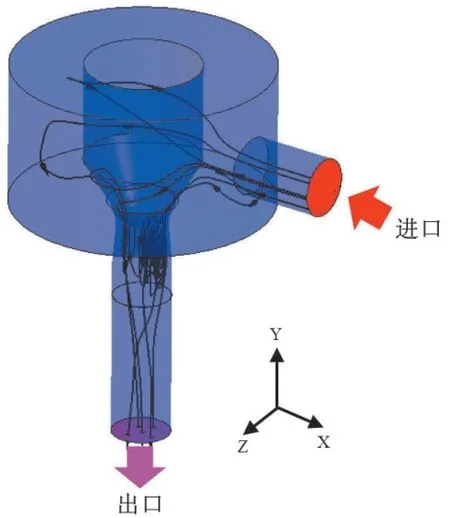
图1 计算模型及边界条件

图2 混合网格

采用CFD软件进行数值计算，采用定常雷诺时均方程（RANS）求解。湍流模型为Shear Stress Transport（SST）。守恒方程中的平流项和湍流输运方程均采用软件中的二阶差分格式。计算残差收敛在10-6左右。

计算网格划分为混合网格结构，在壁面附近的边界层区域设置为结构化网格，结构化网格的y+＜1，递增率为1.1，边界层网格共30层。中间流道远离壁面的地方均采用非结构化网格。图 2中给出了调节阀所使用的网格结构。

参照历史文献[11-12]，采用上述计算方法是准确可靠的。

对网格进行网格无关性验证，使用入口位置总压作为考核参数。通过同步改变各条边上的网格数量改变网格总数，共绘制5套网格，形成的网格无关性曲线如图 3所示，各套网格数量如表2所示。

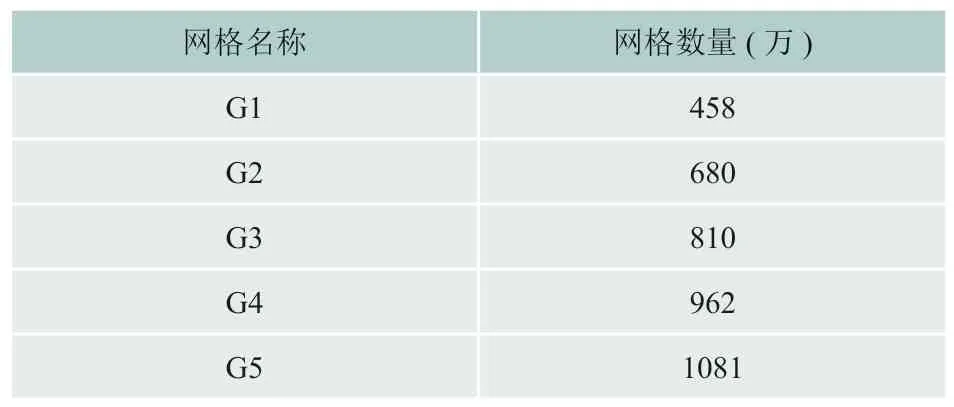
表2 网格数量

表3 高湍动能区最高值（单位：m2/s2）

从图3中能够观察到，当网格数量达到810万后，网格数量对于计算结果基本不再有影响。因此后续计算中均选用G3网格作为后续计算使用分析使用的网格。

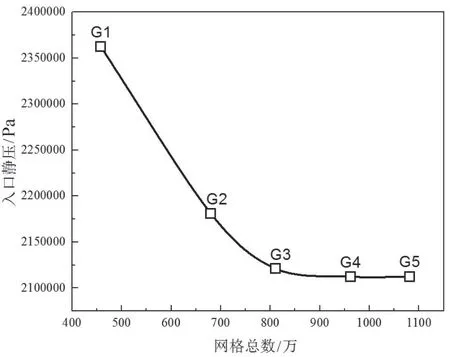
图3 网格无关性曲线

2 空心阀头流动状态分析

图4中给出了空心阀头调节阀的速度云图及流线图分布，图中的Y轴及Z轴与图 1中坐标轴位置相对应。从图4中能够观察到，流体通过喉部之后主要沿着z/Z=0.4～0.6之间的区域紧贴着阀座壁面流入下游。在z/Z=0.55，y/Y=0.7的阀头表面出现了明显的流动分离结构。该流动分离结构对应着阀头型线的结束位置，流道在该位置的面积突扩。该位置的面积突扩后造成的后台阶流动效应是该位置产生边界层分离的主要原因。边界层分离使得z/Z=0.3～0.5，y/Y=0～0.5范围内产生了巨大的肾型涡结构，该结构在速度云图上表现为巨大的低速流动区。

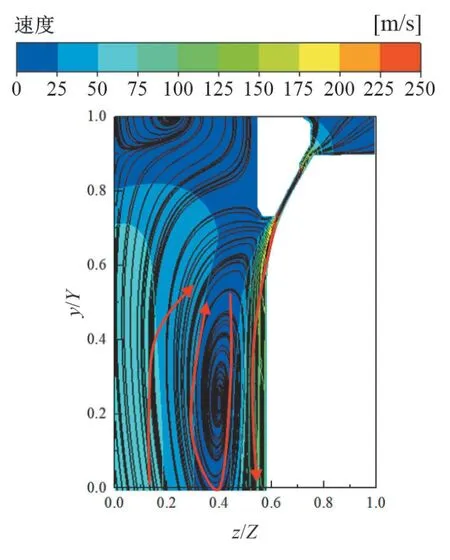
图4 空心阀头速度云图及流线图

图5展示了空心阀头调节阀的湍动能及流线分布，图中的Y轴及Z轴与图 1中坐标轴位置相对应。从图5中能够观察到图中共有两类高湍动能区及鞍点位置。两类高湍动能区分别为喉部位置(HR1TKE；z/Z=0.2，0.8；y/Y=0.7)(HR∶ High Region)及肾型涡区域(HR2TKE；z/Z=0.3～0.4,0.6～0.7；y/Y=0.3～0.7)位置。上述两类高湍动能区的湍动能最高值及位置如图5所示。鞍点在图中为z/Z=0.05，y/Y=0.7。

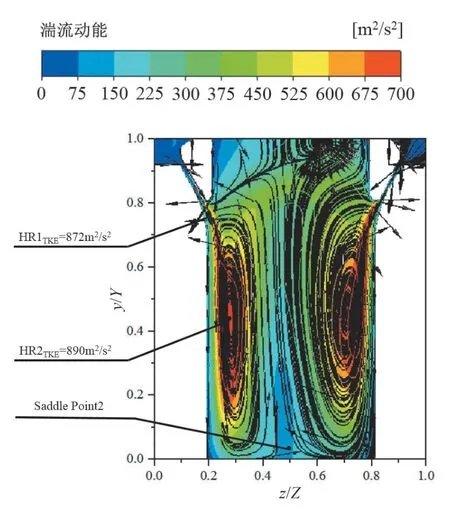
图5 空心阀头湍动能云图及流线图

结合图 4中的流动分析结果能够发现，鞍点为肾型涡的结束位置，流体在鞍点位置分为向上回卷的流体及向下流动的流体两部分。鞍点下游的流动趋势趋于稳定。

流动紊乱区的长度为调节阀座喉口直径的2倍，上述流动紊乱导致的高湍动能区使得调节阀的流动损失大大增加，使得调节阀的通流效率下降。

3 余弦阀头结构及流动分析

通过流动状态分析，发现调节阀后流动紊乱区最早产生于阀头边界层的分离，流动表现为肾型涡的产生以及阀后高湍动能区的出现。而阀头边界层的分离在位置上与阀头型线凹陷及阀门流道面积的突扩位置相对应。因此推测，如果能够消除该位置的阀头型线凹陷并使得阀门流道能够更加光顺，可以使得调节阀的流动状态更为光顺。

结合上述猜想，提出使用三角函数中的余弦函数作为阀头型线。并称其为余弦阀头结构。采用的余弦方程如公式(1)所示。

式中的A表征了阀头的长度，如图 6中所示，A值越大表示阀头长度越大。B表征了阀头的半径，能够通过阀座面积改变该数值的大小以适配到合适的调节阀半径，根据阀座的直径选取的各阀B值均为100。

图6展示了采用上述余弦公式构建的阀头型线，图中Y轴与Z轴与图 1中坐标轴位置相对应。Z=0位置绘制的点划线为中心对称线，改线右侧的阀头型线形状与左侧的阀头型线相同。

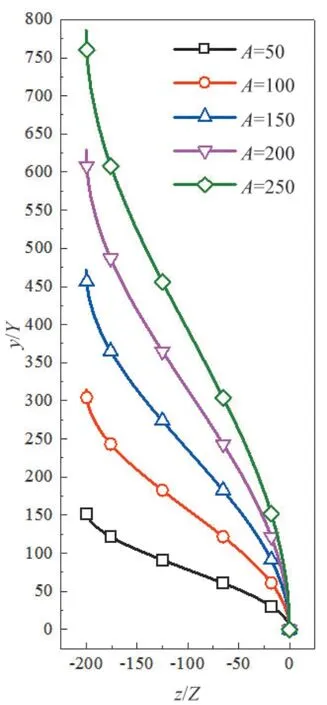
图6 余弦阀头型线

从图6中观察到，余弦阀头能够为流体提供了更加光顺的流道，采用该阀头后有效规避流道面积的突变。随着A的进一步增大，阀头尺寸发生了明显的上升。

图7中给出了A=150余弦阀头的速度云图及流线图，图中的Y轴及Z轴与图 1中坐标轴位置相对应。余弦阀头与前文中空心阀头的流动喉部面积保持一致，网格绘制方法、网格密度及边界条件也与空心阀头保持一致。

图7 A=150余弦阀头速度云图及流线图

从图7中能够观察到流体通过阀头与阀座之间的喉口位置之后，沿着阀头与阀座之间围成的渐扩流道均匀发展。阀座位置在z/Z=0.5，y/Y=0～0.5区域之间形成了一个流动低速区，但是未形成分离泡或边界层分离结构，阀头表面也没有形成分离结构。

图8中给出了A=150余弦阀头的湍动能云图及流线图。图中的Y轴及Z轴与图 1中坐标轴位置相对应。

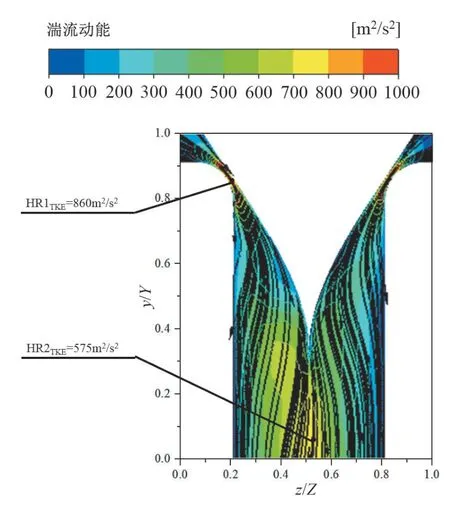
图8 A=150余弦阀头湍动能云图及流线图

从图8中能够观察到，余弦阀头调节阀流动结构中存在两类高湍动能区。分别为喉部位置(HR1TKE；z/Z=0.2，0.8；y/Y=0.9)及余弦阀头末端的下游(HR2TKE；z/Z=0.5；y/Y=0.2)。阀头末端下游的高湍动能区为沿着余弦阀头流至该位置的流体汇聚形成的，在流线图上无法观察到明显的漩涡结构。喉口位置高湍动能区的下降则是由于阀座型线的改型使得该位置流道面积突缩的现象得到了改善。

上述两类高湍动能区的强度相比空心阀头的高湍动能区的数值发生了明显的下降，且由于肾型涡的消失使得原有的高湍动能区类型也发生了减少，各湍动能高区的最高值如表 3所示。高湍动能区的消失及强度的减小表明，A=150余弦阀头相比空心阀头流动更为光顺，通过调节阀后产生的流动损失更小。

4 不同A值的阀头结构流场分析及优选

图9展现了A=50，A=100及A=150三个余弦阀头的湍动能云图，图中的Y轴及Z轴与图 1中坐标轴位置相对应，图中各余弦阀头的流动喉部面积保持一致，网格绘制方法、网格密度及边界条件也均保持一致。

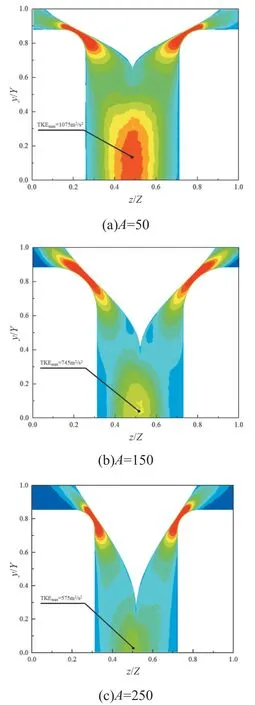
图9 A=50,100,150余弦阀头湍动能云图

图9能够观察到随着A值的不断增加，HR1（喉口位置）的强度与面积基本相同，而HR2（余弦阀头末端的下游）的强度则发生了较为明显的变化。不同余弦阀头HR2位置随着A值的增加逐渐向下移动。其强度也随着A值的增大发生了减小。该高湍动能区最高值的下降是由于阀头位置角度的减小所导致的。随着A值的增大，沿着阀头向下流动的流体在阀头末端位置相撞时候的角度发生了明显的减小。

采用全压损失系数表征各调节阀的经济性，全压损失系数的定义如下：

式中：P1t为进口总压，P2为出口静压；ρ1为进口汽流密度；V1为进口汽流速度。

全压损失系数含义为调节阀造成的出口动能及静压的损失，表征了调节阀造成工作介质总压损失的能力，全压损失系数越大则代表调节阀的总压损失越大，调节阀的经济性能越差。

图10中给出了不同调节阀结构在各个阀门开度下的全压损失系数，横坐标为阀门行程，表征了调节阀阀头与阀座之间的通流面积。纵坐标为全压损失系数。可以看出，各余弦阀头的全压损失系数明显小于空心阀头。随着A值的增加，调节阀的全压损失系数展现出较为明显的下降。当A值增加至200后，A值的进一步上升对于全压损失系数的影响较小。随着阀门开度的上升，各阀门的全压损失系数均明显下降，但是各个阀全压损失系数的排序保持不变。在小开度下，采用余弦阀头减小全压损失系数的效果更为明显，而在大开度下采用余弦阀头仍然能够减小全压损失。

图10 余弦阀头及空心阀头的静压损失系数

综合考虑通流效率及工程设计实用性，选用尺寸较小的Y=100余弦阀头替换空心阀头是较为合适的选择。

5 结论

本文对某型汽轮机调节阀结构进行数值模拟及分析，并针对分析结果提出了余弦阀头结构。

1)目前机组采用空心阀头的调节阀存在阀头边界层分离结构和阀头处的肾涡结构等问题。阀门流道面积的突然增加所导致的后台阶流动现象，使得调节阀后产生了巨大的湍动能区，从而调节阀具有较大的全压损失。

2)针对空心阀头结构的不足，提出一种余弦阀头结构，对比分析了余弦阀头与空心阀头的流动状态。余弦阀头有效地消除了阀头分离及肾型涡的产生，使得调节阀全压损失大大下降。

3)对余弦阀头进行参数化，各参数化后得到的余弦阀头，A值越大的阀头流道全压损失系数越小。但是A值越大的阀头也将使得调节阀结构长度变得更长，并给调节阀头的强度设计带来风险。综合考虑通流效率及工程设计实用性，选用尺寸相近的Y=100余弦阀头替换空心阀头是最为合适的选择。