感应电动机群分组及聚合算法的比较分析

张思阳，陈宇杰，杨浩伯，吴浩 ，鞠平

(浙江大学 电气工程学院，浙江 杭州 310027)

0 引 言

电力负荷作为电力系统的重要组成部分，负荷模型的精度对于电力系统仿真分析的准确性具有重要影响。感应电动机是电力系统中最常见的动态负荷，感应电动机群的等值是负荷建模工作的重要组成部分[1-6]。由于电力系统负荷中的感应电动机数量众多、种类复杂，很难在稳定计算中考虑所有电动机的负荷模型。因此，电力系统仿真分析时通常将单个负荷节点下的众多电动机等值为单台或两台电动机来模拟整个电动机群的负荷特性[7]。

感应电动机群的等值方法包括分组及聚合两个步骤。分组算法通常依据一个或多个特征指标对感应电动机群进行分组。依据单个特征指标的分组算法通常着眼于感应电动机的某一特性，计算过程较为简便，如文献[8]提出，电动机的电磁转矩-滑差特性对电动机的动态特性有很大影响，可将电磁转矩-滑差特性曲线较为相似的电动机划分为一组。文献[9]考虑到各电动机静态临界稳定特性的差异，定义临界滑差与临界电压的比值为特征指标，将指标相近的电动机划分为一组。文献[3,10]提出电动机在电压发生小干扰下的动态特性由其特征值决定，取电动机惯性时间常数与转子电阻的乘积作为特征指标，指标相近的电动机划分为一组。

依据多个特征指标对感应电动机群进行分组时还需选择合适的分组方法，如文献[11]选择与电动机转子电磁暂态特性相关的转子特征值的阻尼比和与机械暂态特性相关的机械特征值的衰减率作为特征指标，基于k-均值聚类算法将电动机群分组。文献[12]选择感应电动机定子电阻、定子电抗、暂态开路时间常数等9个特征指标，使用自组织神经网络将感应电动机群分组。文献[13]选用感应电动机初始滑差、暂态开路时间常数、机械转矩系数与转子堵转等值电抗的乘积等7个特征指标，由模糊c均值聚类算法对感应电动机群分组。

感应电动机的聚合是指确定等值电动机的负荷模型参数，使得等值电动机的外部特性与聚合前多台并联电动机的总体外部特性相同或相近[3]。文献[14]假设所有电动机T型等值电路中性点直接并联，以各电动机的容量为权值，等值电动机的参数为各电动机参数的加权和。文献[15]在加权聚合计算中考虑了负载率和临界滑差的影响对权值进行修正。文献[10]在加权聚合计算中使用感应电动机转子堵转等值电抗和定子开路时间常数对权值进行修正。文献[11]以等值前后电动机负荷具有相同的总吸收有功功率和无功功率、总电磁功率、总转子铜耗、总最大电磁功率和总动能为原则将电动机群等值为一台电动机。文献[12,16]提出将电动机静态电路等效为3个并联阻抗，通过将同一母线下所有电动机的等值阻抗分别并联后，再还原为一台电动机。文献[17,18]假设所有电动机同时处于空载和堵转两种极端状态，依据等值前后总阻抗相等的原则计算等值电动机的负荷模型参数。

单个负荷节点下的感应电动机群中，各感应电动机类型及负荷模型参数各有不同，其负荷特性也存在较大差异，感应电动机群分组的特征指标及多台感应电动机的聚合方法难以确定，目前仍未有公认的最佳等值方法。

本文选择了较为经典的三种依据单个特征指标将感应电动机群分组的分组算法及三种电动机加权聚合法，比较分析了各方法的基本原理，而后采用交叉组合的方式将IEEE推荐的7种感应电动机等值，并在单负荷无穷大系统，比较分析了各等值方法的等值效果。

1 三阶感应电动机模型

由于定子绕组的暂态过程对电力系统动态分析影响不大，因此电力系统机电暂态仿真一般采用忽略定子绕组电磁暂态过程的三阶感应电动机模型[19,20]。感应电动机静态等值电路如图1所示。

图1 感应电动机静态等值电路图

转子电压方程和运动方程如下：

式中：T'd0=(Xr+Xm)/Rr为定子开路时间常数；X=Xs+Xm为转子开路电抗；X'=Xs+XrXm/(Xs+Xm)为转子堵转等值电抗；Rr、Xr、Xm、Xs分别为电动机转子电阻、转子电抗、激磁电抗和定子电抗，Tj为转子惯性时间常数；ωr=1−s，s为转子滑差；E'd、E'q分别表示感应电动机直轴暂态电势和交轴暂态电势；Id、Iq分别表示感应电动机定子直轴和交轴电流；TE、TM分别表示感应电动机电磁转矩及机械转矩，其方程见式(3)―(4)。

定子直轴和交轴电流Id和Iq方程为：

式中：Ud、Uq分别表示感应电动机直轴和交轴电压；Rs为感应电动机定子电阻。

感应电动机电磁转矩TE和机械转矩TM分别为

式中：T0为稳态机械转矩；A、B、C为机械转矩系数，满足Aω02+Bω0+C=1，ω0=1-s0，s0为转子初始滑差。

2 感应电动机分组算法

由上文引言所述，依据单个特征指标将感应电动机群分组的算法，其分组依据的物理含义较为明确，且计算简单，因此本文选择经典的基于感应电动机临界稳定特性及动态特性的特征指标及感应电动机的电磁转矩-滑差特性曲线等三种特征指标将感应电动机群分组并比较分析。

2.1 基于感应电动机静态临界稳定特性分组

文献[9]分析了感应电动机负荷的静态临界稳定特性，提出当单个负荷节点下的若干台电动机遭受大扰动时，稳定能力较弱的电动机可能会发生堵转并吸收大量无功功率，导致负荷节点电压下降，稳定能力较强的电动机则保持稳定。考虑电动机群稳定能力的强弱有利于改善电动机群聚合等值的准确性[9]，因此，选择感应电动机临界电压及临界滑差两个能够反映电动机稳定能力的参数作为电动机群分组的依据。

根据图1所示的感应电动机静态等值电路，感应电动机的电磁转矩可以表示为[21]：

其中Zs=Rs+jXs，Zr=Rr/s+jXr，Zm=jXm。稳态时，电动机滑差s和电压U须满足转矩平衡方程，令TE=TM，即

当U=1时，感应电动机的最大电磁转矩所对应的滑差为临界滑差scr，临界滑差可由下式确定

将临界滑差代入式(6)，可得感应电动机的临界电压Ucr。定义感应电动机临界特征gcr，如式(9)所示。

稳定能力较差的电动机，其对应的临界特征指标gcr较小，分布也较为集中，易于区分。在实际计算中，可根据gcr值将感应电动机群进行分组。

2.2 基于感应电动机动态特性分组

文献[3,10]提出，当单个负荷节点下的若干台电动机遭受小扰动时，各电动机的转矩、滑差变化等动态特性各有区别。考虑感应电动机在小扰动下的动态特性差异有利于提高电动机群聚合等值的精度[3,10]。因此，选择感应电动机动态过程特征值这一能够反映感应电动机在电压发生小干扰下的动态特性的参数，作为电动机群分组的依据。

由式(1)中的转子运动方程可得，感应电动机转子运动的状态方程为

为了简化定性分析，假设机械转矩TM恒定，可得

将式(11)在额定滑差sN附近线性化，可得

其中

由于sN一般较小，因此

由式(10)、式(12)和式(14)可得线性化状态方程

由于接在同一母线上的各电动机的端电压相同，因此定义动态特征指标gdy，如式(16)所示。

当几台电动机的动态特征指标gdy相近时，其动态特性较为相似，可将其分为一组。

2.3 基于感应电动机电磁转矩-滑差特性曲线分组

文献[8]提出，负荷节点下的若干台电动机遭受扰动后，其动态特性受电磁转矩-滑差特性的影响。因此在电动机群分组时，可考虑将电磁转矩-滑差特性曲线较为相似的电动机划分为一组。

感应电动机电磁转矩TE、机端电压U、阻抗参数和滑差s的关系可由式(5)表示。以国内某四台典型电动机参数为例[20]，令U=1，做出TE-s曲线如图2所示，为了便于比较，TE-s曲线作归一化处理。

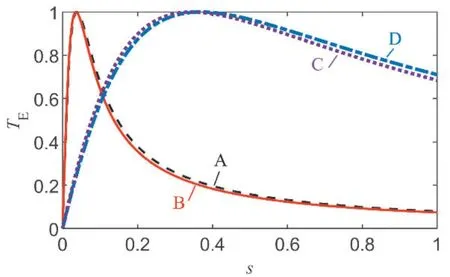
图2 典型感应电动机TE-s曲线

将滑差s在0～1范围内采样，采样间隔为0.005，计算各电动机在各采样点上的电磁转矩。定义任意两条曲线之间的距离dmn，如式(17)所示：

式中：N为采样点数；分别为曲线m和曲线n在第i个采样点上的电磁转矩值。图2所示4台电动机电磁转矩-滑差特性曲线的距离如表1所示。

A―0.0012 0.0482 0.0476 B 0.0012―0.0489 0.0481 C 0.0482 0.0489―0.0015 D 0.0476 0.0481 0.0015―

由图2及表1，根据曲线相似性，可将曲线A、B代表的电动机划分为一组，曲线C、D代表的电动机划分为一组。

3 感应电动机聚合算法

感应电动机的聚合算法中，最为经典的是基于电动机额定容量的加权聚合法[3,8,10]。因此，本文选择该方法及两种加权因子修正的加权聚合法将多台感应电动机群聚合并比较分析。

3.1 基于电动机额定容量的经典加权聚合法

文献[14]提出，连接在同一负荷点上的感应电动机是并联连接的，因此假定所有电动机静态等值电路中的三条支路都直接两端并联，即图1中各电动机等值电路的内节点K相连接，以各电动机额定容量占总容量的比值作为权重，加权综合得到等值感应电动机负荷模型参数。

每台感应电动机的额定容量为

式中：P0为负荷点总有功功率，pper.i、Lf.i分别为每台感应电动机消耗的有功功率占负荷点总有功功率的比例及负载率。

每台感应电动机的加权因子acl.i为

等值电动机的各支路参数为

式中：Zag为等值电动机的支路阻抗；Zi为每台电动机的支路阻抗，包括定子支路阻抗Zs、激磁支路阻抗Zm和转子支路阻抗Zr（参数定义同上文2.1节）。感应电动机惯性时间常数Tj、机械转矩系数A和B参数等均采用多台感应电动机参数的加权值。

3.2 基于电动机负载率和临界滑差修正的加权聚合法

文献[15]提出，连接在同一负荷点上的多台电动机运行工况不同，其运行工况由各电动机的负载率和临界滑差决定。上文3.1节提出的基于电动机额定容量的经典加权聚合法仅考虑电动机容量这一结构性参数，而未考虑各电动机运行工况的差异对电动机聚合的影响，因此基于电动机负载率和临界滑差对加权因子进行修正。

定义考虑电动机运行工况的加权因子aop.i为

式中：scr.i、Lf.i分别为各感应电动机临界滑差、负载率。

由式(22)可以看出，该修正是为了增加负载率大和临界滑差小的电动机的权重。考虑到电动机运行工况的差异对定子支路和转子支路的聚合有明显影响，对激磁支路及其他电气参数的聚合影响弱。因此，计算等值感应电动机定子支路和转子支路参数时使用式(21)定义的加权因子aop.i替换式(19)中的acl.i，其余参数计算仍使用acl.i计算。

3.3 基于电动机转子堵转等值电抗和开路时间常数修正的加权聚合法

文献[10]提出，当负荷点电压、频率发生扰动时，负荷点上连接的电动机有功功率、无功功率变化的特性受感应电动机转子堵转等值电抗X'和定子开路时间常数T0'的影响较大，当感应电动机的X'或T0'增大时，其动态过程中功率振荡的幅值减小。上文3.1节提出的基于电动机额定容量的经典加权聚合法未考虑电动机动态过程的差异，因此在对感应电动机群聚合时，需要使用上述两个参数对加权因子进行修正。

感应电动机的转子堵转等值电抗X'和定子开路时间常数T0'定义同式(1)。定义考虑电动机动态过程的加权因子ady.i为

由式(24)可以看出，该修正是为了增加转子电阻、转子电抗和定子电抗较小的电动机的权重。使用式(23)定义的加权因子ady.i替换式(19)中的acl.i，加权综合得到等值感应电动机的各电气参数。

4 感应电动机群仿真算例的比较分析

由上文第2、3节，选择的三种单一指标的分组算法及三种不同加权因子的加权聚合法均依据不同的原则或假设。为了比较分析不同分组及聚合算法组合后的等值效果，本文将三种分组算法及三种聚合方法交叉组合后，对多台感应电动机进行等值，并在单负荷无穷大系统中对比分析不同等值方法的等值效果。

4.1 感应电动机群分组及聚合结果

4.1.1 感应电动机群暂态仿真分析

选择IEEE提供的工业小电动机、工业大电动机、水泵、厂用电、民用综合电动机、民用和工业综合电动机、空调综合电动机等7种典型感应电动机[22]作为三种分组算法及聚合算法比较分析的感应电动机群算例，其负荷模型参数如表2所示。为了比较各典型电动机负荷特性之间的差异，采用图3所示的方法单负荷无穷大母线系统对各电动机进行暂态仿真。

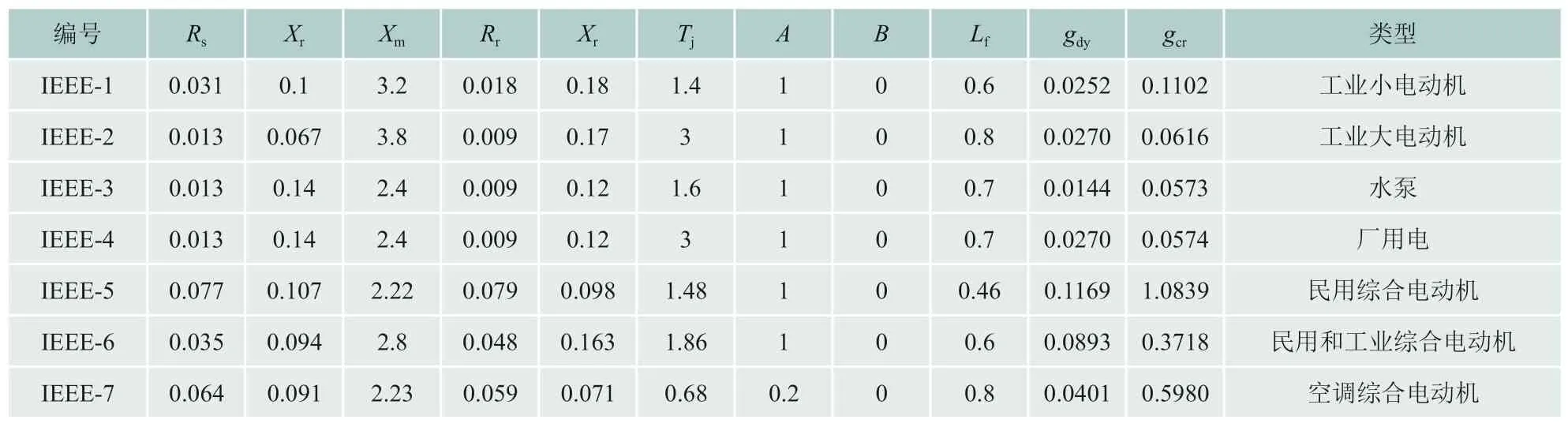
表2 IEEE典型电动机参数

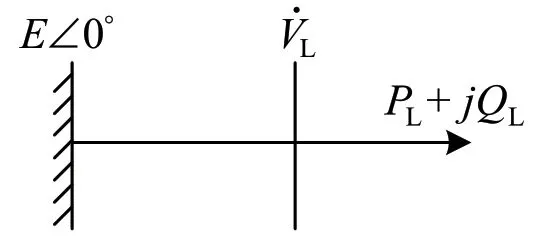
图3 单负荷无穷大系统

设稳态时，无穷大节点电压E=1.05，负荷节点电压V=1，负荷节点功率为PL0+jQL0=1+j0.4pu，系统的基准容量为100MVA，负荷由感应电动机负荷和恒阻抗负荷构成，感应电动机负荷占比60%[22]。设置负荷节点在0.06s时发生三相金属短路故障，故障持续0.2s后清除，仿真步长为0.01s，记录1.5s内的动态响应数据。分别连接7种感应电动机时，负荷节点的电压、功角、有功功率和无功功率仿真曲线如图4(a)至(d)所示。

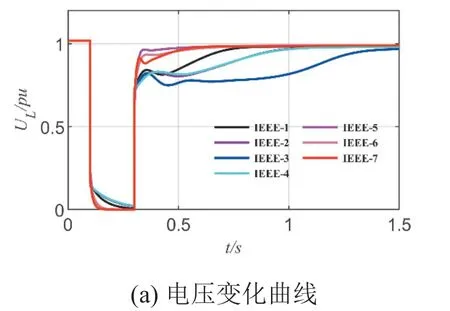
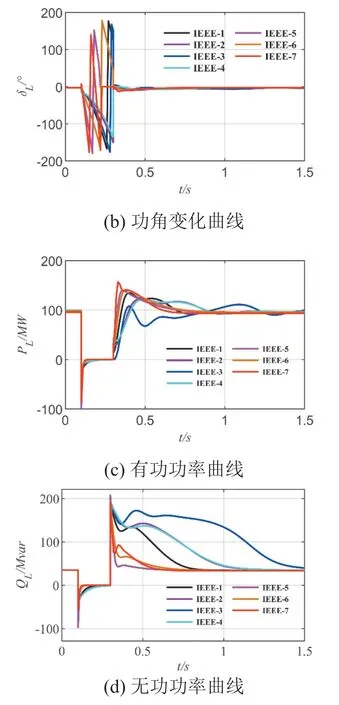
图4 IEEE 7种典型感应电动机暂态响应曲线

从图4(a)、4(b)来看，当负荷节点连接不同电动机时，负荷节点的电压及功角具有不同的暂态恢复过程，其中有5种电动机在故障期间已经出现功角振荡现象。从图4(c)、4(d)来看，当机端电压发生变化时，7种感应电动机的有功功率、无功功率响应曲线差异明显，具有不同的振荡及恢复过程。因此，IEEE推荐的7种感应电动机一定程度上能够反映出工程中一个负荷点下多台感应电动机负荷的差异性。

4.1.2 电动机群分组及其聚合参数

以上文第3节提出的三种分组算法将IEEE推荐的7种典型感应电动机分组。依据感应电动机临界特征指标gcr和TE-s特性曲线分组结果相同，如表3所示，7种感应电动机TE-s特性曲线如图5所示。依据感应电动机动态特征指标gdy分组的结果如表4所示。

表3 依据临界特征指标gcr、TE-s曲线分组结果

表4 依据动态特征指标gdy分组结果

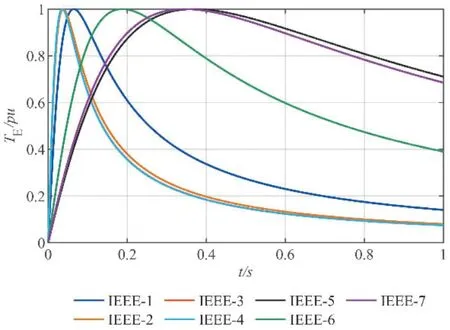
图5 7种IEEE典型感应电动机电磁转矩-滑差特性曲线

由图4(a)的电压变化曲线及图4(d)无功功率曲线，IEEE-(1-4)、IEEE-(5-7)等两组电动机的暂态恢复过程较为接近，与表2所示的依据感应电动机临界特征指标gcr和TE-s特性曲线分组结果较为吻合。

在表3和表4的分组结果基础上，计算各聚合算法所得等值感应电动机的负荷模型参数，结果见表5和表6。

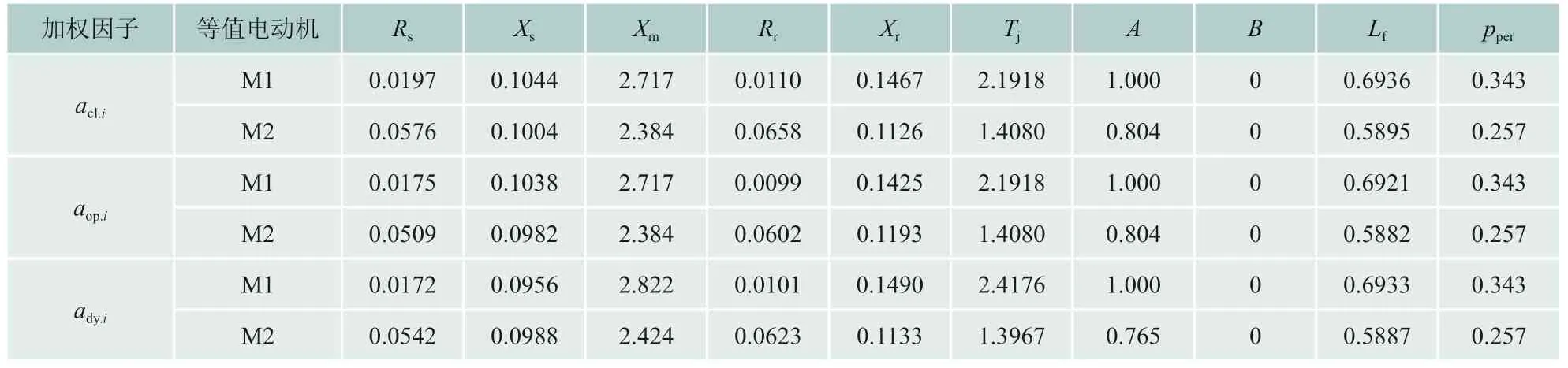
表5 依据gcr或TE-s特性曲线分组结果的各聚合算法所得等值电动机参数

表6 依据gdy分组结果的各聚合算法所得等值电动机参数

4.2 单负荷无穷大系统下的等值效果

将原始电动机群及不同等值感应电动机接入单负荷无穷大系统，比较分析不同等值方法的等值效果。单负荷无穷大系统的接线图如图3所示，参数及故障设置同上文4.1.1节。等值前后负荷节点电压、功角、有功功率和无功功率的仿真结果如图6所示。

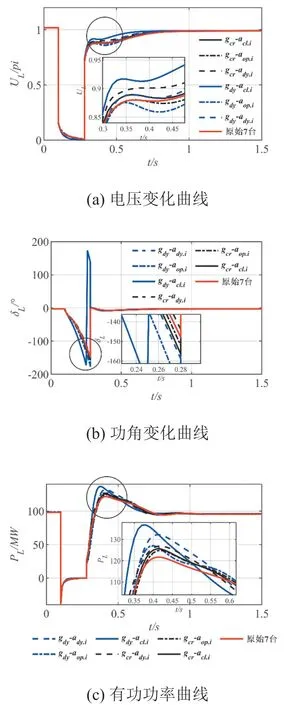
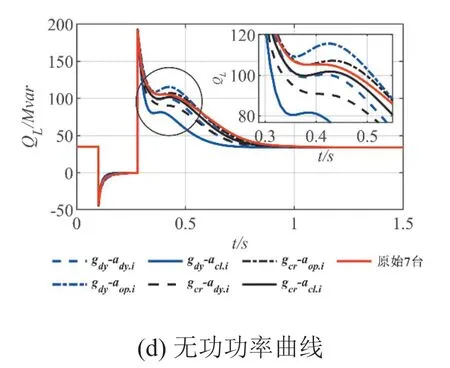
图6 不同感应电动机群分组及聚合算法仿真结果

由图6(a)―6(d)，不同等值方法所得等值感应电动机的仿真结果存在差异，且在无功功率的等值效果上差异最为明显。另外，采用感应电动机动态特征指标gdy分组后，以基于感应电动机额定容量的加权因子acl.i的经典加权聚合法所得感应电动机在故障持续8个周波时，功角发生振荡，等值效果较差。

为了量化各等值方法的等值效果，定义电压误差指标：

式中：Ugi和Uci分别为原7种电动机和等值电动机时的节点电压幅值仿真曲线上第i点的值；N为仿真取样点数。功角误差指标、有功功率误差指标、无功功率误差指标分别用εδ、εP、εQ表示，定义与式(25)类似。各等值方法所得等值电动机模型的仿真误差指标如表7所示。

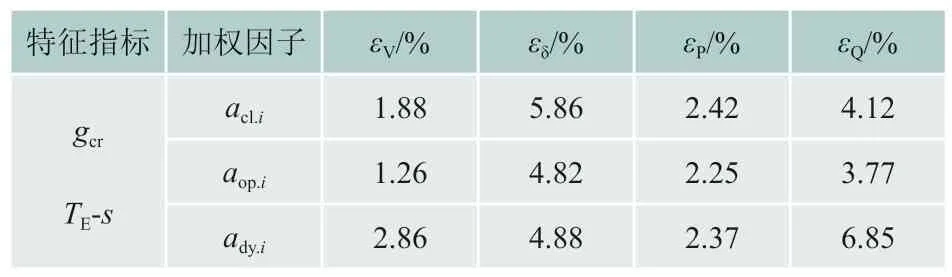
表7 不同等值方法的误差指标比较

由图6和表7可以看出，不同感应电动机分组算法及聚合算法交叉组合后，其等值效果之间具有明显差异：

1)依据感应电动机临界特征指标gcr和TE-s特性曲线分组后的等值效果优于依据动态特征指标gdy分组。依据感应电动机临界特征指标gcr和TE-s特性曲线分组时，各方法仿真误差均不超过8%。而依据动态特征指标gdy分组时，三种聚合算法的多个仿真误差指标大于10%，等值效果较差。

2)基于电动机负载率和临界滑差修正的加权因子aop.i的加权聚合法的等值效果优于其他两种加权聚合法，不同分组算法下，该方法的仿真误差均小于其它两种加权聚合法。依据感应电动机临界特征指标gcr和TE-s特性曲线分组后，该方法的各仿真误差小于5%。

5 结论

本文首先比较分析了三种感应电动机群分组算法和聚合算法的基本原理，而后采用三种分组算法和三种聚合算法交叉组合的方式将IEEE推荐的7种感应电动机等值，最后将原始电动机群和等值电动机接入单负荷无穷大系统，比较分析了各等值方法的等值效果。研究发现：

1)对于分组算法，依据感应电动机的临界特征指标gcr或TE-s特性曲线分组考虑了电动机在遭受大扰动后的动态特性，等值效果优于依据感应电动机的动态特征指标gdy分组。

2)对于聚合算法，以基于电动机负载率和临界滑差修正的加权因子aop.i的加权聚合法考虑了电动机的运行工况，在三种不同分组算法下，该方法的误差均小于其它两种加权聚合法，等值效果较好。

3)三种分组算法和三种聚合算法交叉组合后，不同等值方法的等值效果有明显差异。其中，依据感应电动机临界特征指标gcr或TE-s特性曲线将感应电动机群分组后，以基于负载率和临界滑差修正的加权因子aop.i的加权聚合法将多台感应电动机聚合的等值方法，其等值效果优于其它等值方法。

下一步工作将致力于比较多种感应电动机群的分组及聚合算法，在更加复杂的运行条件下研究各等值方法对感应电动机群等值精度的影响。