类星舰飞行器翻转着陆轨迹优化
鲁 鹏,李雅轩,刘新福
(北京理工大学宇航学院,北京,100081)
0 引 言
航天运输系统是开展空间活动的核心支撑,是发展航天事业、建设航天强国的基本前提,是加速发展空间科学技术、和平开发空间资源和维护国家空间安全的重要保障[1]。近年来,随着人类空间资源开发需求的快速增长,可重复使用运载器受到了全球的广泛关注,世界各主要航天大国积极开展了相关的理论研究和工程实践[2]。
瞄准星际移民和深空探测的目标,美国太空探索技术公司(SpaceX)研制了名为星舰(Starship)的新一代可重复使用航天运输系统。2016 年9 月,SpaceX 公司正式对外公布了“星际运输系统”方案[3]。此后,星舰设计方案经历了多次重大改进和演化。自2020 年起,通过开展密集的飞行测试,SpaceX 公司逐步掌握了150 m 低空悬停、10 km 高空飞行、翻转机动和垂直定点软着陆等关键技术,项目取得重大进展。值得关注的是,星舰采取了与传统航天器截然不同的着陆方式:着陆前,星舰采用90°左右大攻角飞行,在视觉上以腹部平拍的姿态向地面飞行;接近地面时,星舰发动机开机进行推力矢量控制,联合首尾四个气动舵,完成姿态由水平向垂直的快速翻转,并控制星舰减速和修正位置误差,实现定点软着陆[4]。图1展示了该特殊的着陆过程。这种独特的着陆方式对飞行器的轨迹优化设计提出了新的挑战。大范围的姿态机动和复杂的约束条件必须在优化设计翻转着陆飞行轨迹时得到充分的考虑。
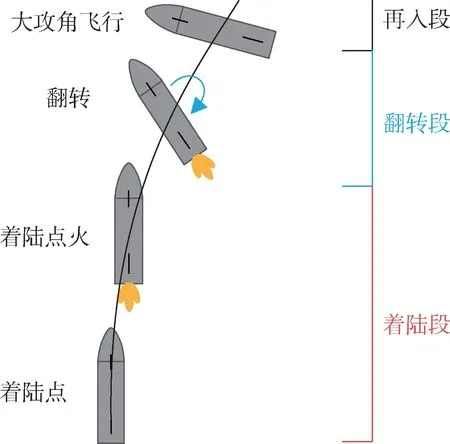
图1 类星舰飞行器翻转着陆过程示意Fig.1 The flipping and landing process of a starship-like vehicle
近年来,凸优化方法被广泛地应用于飞行器轨迹优化设计,特别是在解决星际探测器、运载火箭等常规航天器的着陆轨迹优化问题时发挥积极作用[5]。美国喷气推进实验室的Açıkmeşe 等[6]通过使用无损松弛和变量替换等方法将带有非凸推力约束的火星着陆轨迹优化问题转化为凸优化问题,显著提高了轨迹优化算法的可靠性和计算效率。Szmuk等[7]对六自由度火星动力下降制导问题进行了深入研究,通过设计序列凸优化算法计算考虑姿态动力学的着陆飞行轨迹。相比于火星着陆,因为气动力不可忽略,运载火箭着陆在地球表面的轨迹优化问题求解难度更大。刘新福[8]将推力和攻角同时作为控制量,把对应的燃料最优着陆问题顺利转化为凸优化问题进行迭代求解,并理论证明了所采用松弛技术的有效性。杨润秋等[9]将该研究工作拓展到飞行时间自由的问题,用高度代替时间作为自变量对优化问题进行重构,并基于序列凸优化设计了轨迹优化算法,其中使用的非线性保留技术被证实可以有效提升算法收敛性。
尽管上述方法能够有效解决常规航天器的着陆轨迹优化问题,但对类星舰飞行器的翻转着陆轨迹优化并不太适用。原因在于类星舰飞行器在滑翔段和着陆段之间存在独特的翻转过程。大范围的姿态机动导致类星舰飞行器不能被简单地处理为质点模型,而必须在设计着陆轨迹时考虑姿态动力学和因姿态控制产生的复杂约束条件。但是,目前针对此类轨迹优化问题的研究非常有限。
本文针对类星舰飞行器的翻转着陆轨迹优化问题进行了深入研究。首先根据类星舰飞行器在翻转着陆阶段的飞行力学特征和任务特点,建立考虑姿态机动和典型约束条件的翻转着陆轨迹优化问题。然后研究将该优化问题通过凸化方法转化为凸优化问题,进而设计迭代算法序列求解。通过提供合理的初值、引入虚拟控制和在目标函数中惩罚信赖域半径等方法,该迭代算法表现出良好的收敛性。针对发动机摆角振荡问题,本文提出将发动机摆角响应引入动力学,这种处理被证实能够有效抑制发动机摆角振荡,并有利于迭代算法的收敛。此外,依托轨迹优化算法,本文亦分析了发动机个数和优化目标选取等因素对类星舰飞行器翻转着陆过程的影响,相关数值结果可以为类星舰飞行器的翻转着陆轨迹优化设计提供参考。
1 翻转着陆轨迹优化问题
1.1 动力学建模
本文将研究类星舰飞行器在二维平面内考虑一个姿态角的翻转着陆轨迹优化问题。再入过程中飞行器控制能力强,通常可使飞行器再入终端速度矢量和着陆点位于同一垂直平面内,而着陆过程中的侧向运动通常会消耗额外燃料,因此在进行类星舰飞行器轨迹优化时可以忽略侧向运动。实际飞行时,着陆过程中的侧向位置误差可以通过控制进行修正。构造类星舰飞行器翻转着陆轨迹优化问题时会使用到着陆坐标系Oxy和体坐标系Obxbyb,如图2所示。
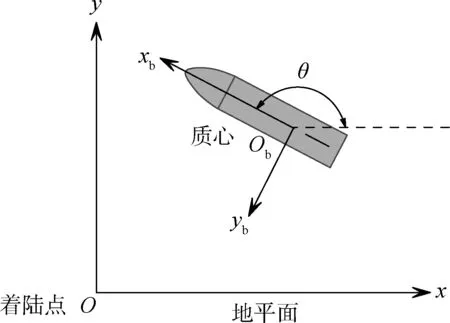
图2 着陆坐标系Oxy和体坐标系Obxb ybFig.2 The definition of landing coordinate system Oxy and the body-fixed coordinate system Obxb yb.
图3a 展示了飞行器翻转着陆过程受力分析结果,根据牛顿第二定律建立动力学方程。为了避免在问题求解时出现数值问题,需要对动力学方程中的物理量进行无量纲化处理。长度的无量纲系数为飞行器初始高度ry0,速度无量纲系数为ry0g0(g0是地球表面重力加速度),时间无量纲系数为ry0g0,质量无量纲系数为初始质量m0。着陆坐标系下,无量纲的飞行器翻转着陆的动力学方程,记为ẋ(t) =f(x(t),u(t)),如下:
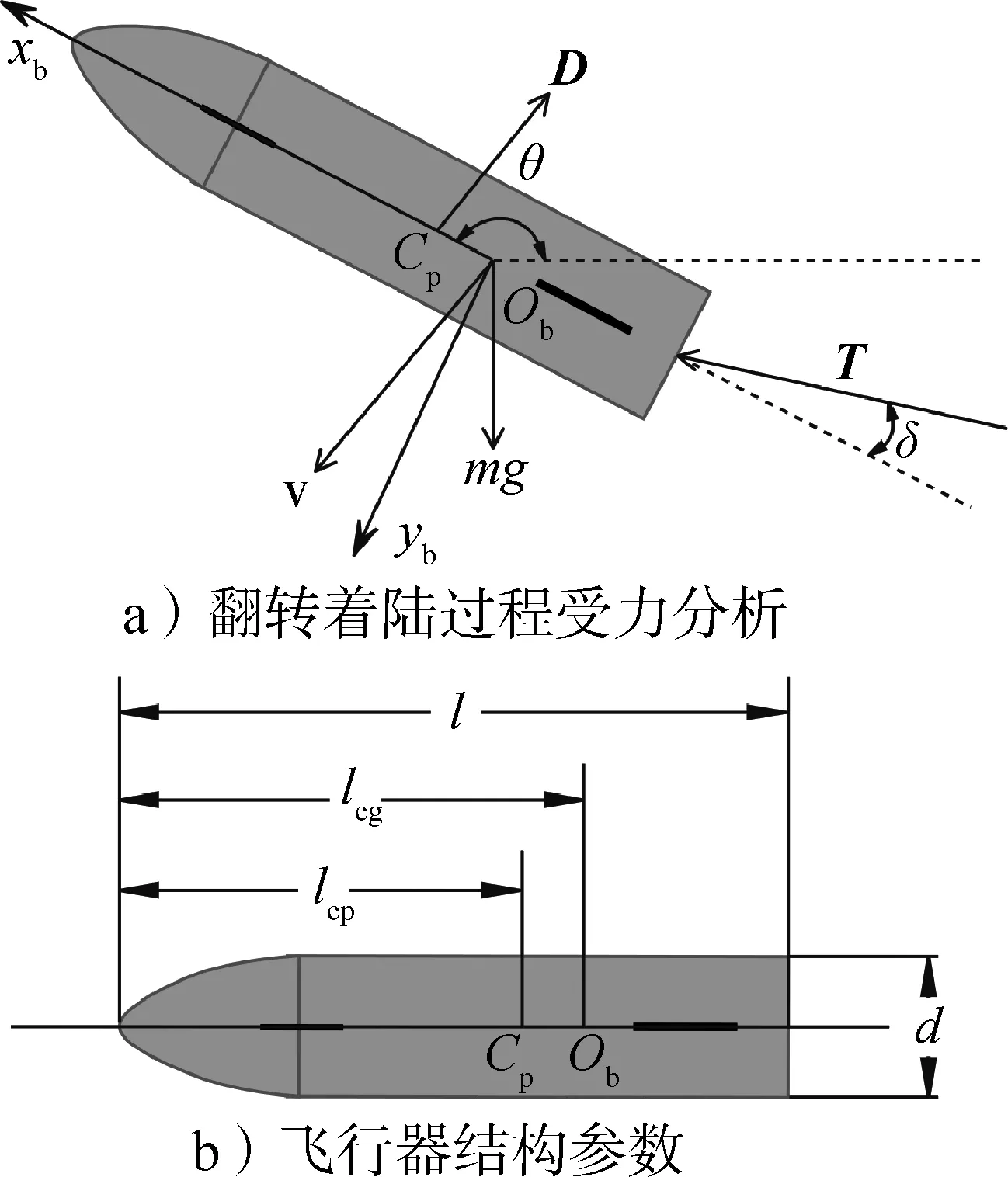
图3 飞行器受力分析和结构参数Fig.3 Force analysis and structural parameters of the vehicle
式中r∈R3为飞行器位置矢量;v∈R3为飞行器速度矢量;m为飞行器质量;T为发动机推力矢量;T为推力矢量的模,T=‖T‖;D为气动阻力矢量;g为重力加速度矢量;θ为飞行器俯仰角(定义见图2);ω为俯仰角速度;MT为推力产生的力矩;MD为阻力力矩;Jz为飞行器绕质心的转动惯量;αe为质量消耗率,αe=-1Isp,Isp为发动机比冲;δ为发动机摆角;δd为δ的响应;Td为一阶惯性环节的无量纲时间常数。本文将发动机摆角视为控制变量,它同时控制位置和姿态,进行轨迹优化时会导致严重的发动机摆角振荡。鉴于此,本文将发动机摆角响应引入动力学(见式(6))。数值仿真结果表明,这一思路将有效抑制发动机摆角振荡现象,进而提高了2.3 节设计的轨迹优化算法的收敛性。x为状态变量,x=[rTvTθ ω m δd]T,u为控制变量,u=[T δ]T。本文将动力学投影在着陆坐标系中,因此无量纲的推力T、阻力D以及相应推力力矩MT和阻力力矩MD的计算公式如下:
1.2 其它约束条件
飞行器翻转着陆轨迹优化不仅受到动力学方程的约束,还有端点约束和过程约束,接下来详细介绍这些约束。
飞行器初始状态约束可以表述成Φ= 0 的形式。本优化问题给定初始位置r(1)0、速度v(1)0、俯仰角θ(1)0、俯仰角速度ω(1)0和初始质量m(1)0,本文使用上标“(1)”标记翻转段对应的量,使用上标“(2)”标记着陆段对应的量。因此Φ具体表达式如下:
翻转着陆过程中飞行器不能有向上的速度,即竖直速度vy不能为正,因此得到速度约束:
为了保证翻转过程中飞行器姿态在合理范围,保证着陆过程飞行器垂直着陆,翻转着陆过程施加如下关于俯仰角的边界约束:
考虑到飞行器在载人时的舒适性和姿态控制系统的能力,姿态角速度不能超过最大值ωmax,即有:
发动机的最大摆角记为δmax,故摆角需要满足:
发动机摆角速度不能超过最大值δ̇max,可以通过约束发动机摆角响应的变化率δ̇d实现对发动机摆角速度的限制,由式(6)可知,需引入如下限制发动机摆角速度的约束:

式中n为发动机个数,n∈N+。
为了方便垂直着陆,每个时刻飞行器和着陆点连线与竖直方向的夹角不能大于给定角度γgs,这就需要添加下滑道约束:
式中ry为位置矢量在着陆坐标系y轴方向的分量。该下滑道约束是一个二阶锥约束。
过程约束(12)~(18)可以改写为如下不等式约束:
末端等式约束可以表示为E=0 的形式,本优化问题中飞行器将着陆到给定位置r(2)f,与此同时末端速度到达给定值v(2)f、俯仰角到达θ(2)f并且俯仰角速度到达ω(2)f。因此,E具有如下形式:
由于燃料有限,终端质量需要满足m(2)(t(2)f)≥mdry,mdry为燃料耗尽时飞行器的质量。
飞行器在翻转段和着陆段交接点处的飞行状态应当连续,连接约束可以表示为Ψ=0,其中:
翻转段耗时、着陆段耗时和翻转着陆段总飞行时间满足约束:
式中tmin为总飞行时间下界;tmax为总飞行时间上界。
1.3 翻转着陆轨迹优化问题
在优化类星舰飞行器翻转着陆的轨迹时,为节约燃料,同时保证翻转结束时飞行器高度不能太低,设计了如下目标函数:
式中μ为惩罚系数,调节μ可以改变翻转段结束时飞行器的离地高度。当μ= 0 时,该优化目标将转化为翻转着陆过程燃料最优。本文3.4 节将详细探讨该惩罚系数的取值对翻转着陆轨迹的影响。
综上所述,可以构造翻转着陆轨迹优化问题P0:
问题P0的本质是多阶段飞行时间自由的最优控制问题。因为动力学约束非线性很强,P0 求解难度较大。
2 凸优化求解
本节将介绍使用改进的序列凸优化(Sequential Convex Programming,SCP)算法求解飞行时间自由的类星舰飞行器翻转着陆轨迹优化问题的方法。虽然序列凸优化算法无法保证收敛,但是可以使用一些方法提高其收敛性。为了提高收敛性,求解问题P0时引入虚拟控制,惩罚信赖域半径[10],并给出了初值选取方法。为了公式的简洁性,本节不再添加区分翻转段和着陆段的上标“(i)”。
为了将飞行时间自由的最优控制问题P0转化为等价的飞行时间固定的最优控制问题,引入变量τ=(t-t0)/Δt,其中Δt=tf-t0表示该阶段耗时,t0是该阶段的初始时间,tf是该阶段的终端时间。将动力学方程转换为以τ∈[0,1]为自变量的形式:
式中 上标“'”表示变量对τ求导。状态变量和控制变量是t的函数,同样也是τ的函数,故有:
当以τ作为自变量时,初始状态约束是τ= 0时的状态约束,终端状态约束是τ= 1时的状态约束。
2.1 线性化
线性化可以将上述非线性动力学方程(25)转化为线性动力学方程。将方程(25)在上一次迭代得到的解附近泰勒展开并保留常数项和一阶项,用展开后的线性方程近似原本的非线性动力学方程。这里将上一次迭代得到的解记为z[k](τ) ≔[(x[k])T(u[k])T]T,时间记为Δt[k],那么在z[k](τ)和Δt[k]附近线性化方程(25),可以得到如下线性动力学方程:

为了构造凸优化问题,除了动力学方程外其它非凸约束也需要进行线性化处理,例如:假设sn(z)是关于z的非凸函数,则如下约束是非凸约束:
使用一阶泰勒展开,略去高阶项,sn(z(τ))≤0 可以由如下线性不等式约束近似:
而问题P0 中除了动力学约束外没有其它非凸约束。
2.2 离 散
为了将连续时间最优控制问题转化为非线性规划问题,需要对连续时间最优控制问题进行离散。将τ所在的区间[0,1]离散成N份,0 =τ0<τ1< …<τN=1,式中τ0,τ1,…,τN是离散节点,与自变量对应的状态 离 散 点 记 为x0,x1,…,xN,控 制 离 散 点 记 为u0,u1,…,uN。离散动力学的数值方法有很多[11],包括欧拉法、梯形法、零阶保持器和一阶保持器等,本文使用梯形法。线性化后的动力学方程(26)经梯形法离散得到线性等式:
式中hj=τj+1-τj。
动力学以外的其它约束,例如sn(z(τ)) ≤0,离散形式是每个离散节点上都满足相应约束:
2.3 虚拟控制和惩罚信赖域
非线性动力学和其它非线性约束经过线性化后,可能使原本可行的问题变成不可行的问题。为了解决由线性化导致的问题不可行,在动力学方程(29)上添加虚拟控制。离散的动力学方程(29)添加虚拟控制vc(τ) ∈R8后 得 到 等 式 约 束(31), 记 为
式中vcj=vc(τj),虚拟控制vcj可以保证任意下一个节点处的状态xj+1都是可以达到的。需要注意,如果序列凸优化算法收敛时虚拟控制的值不为零,则得到的结果就不满足线性化前的动力学约束。为了使程序收敛时虚拟控制为零,需要在目标函数中增加关于虚拟控制的惩罚项Jvc,并且需要为虚拟控制设置一个较大的惩罚系数λvc,本文使用的Jvc如下:
为了保证线性化的合理性,需要添加信赖域约束。本文使用可变信赖域,信赖域作为惩罚项放在目标函数中,即在目标函数中添加关于信赖域的惩罚项Jtr:
式中λtr为惩罚系数。这种以添加惩罚项的方式处理信赖域半径的方法通常可以使问题收敛得更快。λtr取值一般较小,因为当该值较大时,前后两次迭代的结果相差较小,会导致序列凸优算法收敛速度变慢,并且很容易收敛到初值附近的可行解。
至此,可以得到时间自由的两阶段轨迹优化问题P0被凸化后的优化问题P1。本文在翻转段将τ离散为N1等份,在着陆段将τ离散为N2等份。
序列求解凸优化问题P1,当Jvc< ϵvc并且Jtr<ϵtr时程序收敛,即可得到问题P0的解,ϵvc和ϵtr是给定的收敛判据,都是很小的正值。本文算法流程如图4所示。

图4 轨迹优化算法流程Fig.4 Flow chart of trajectory optimization algorithm
2.4 初值选取
对于动力学和其它约束较为简单的优化问题,在使用序列凸优化算法求解时,通常可以直接使用线性初值。而对于本文构造的动力学非线性很强的优化问题,由于线性初值表现不佳,很容易造成算法1收敛慢或无法收敛的情况。为了提高算法1的收敛性,在这里给出一种选取更好初值的方法。
在求翻转段初值时,先忽略翻转过程中气动阻力产生的力矩,然后给定发动机推力和摆角,积分到俯仰角等于给定的θs且垂直速度等于vys时结束,积分结果作为翻转段初值。θs取90°附近的值便于后续垂直着陆。速度vys不能太大,需要保证着陆时速度能减到0。在计算着陆段初值时,求解在问题P0着陆段基础上简化得到的凸优化问题,以简化问题的解作为着陆段初值。具体来说就是给定简化问题的着陆时间,忽略气动力,关于速度的动力学方程不考虑质量变化,不考虑姿态动力学和发动机摆角,并满足部分过程和终端约束,即求解如下凸优化问题:
式中x0取翻转段末端状态;γT为推力方向和y轴间允许的最大夹角;ε为松弛变量;不使用ε计算初值的优化问题可能无解。 上述优化问题中不包括θ,ω,δ,δd。俯仰角θ根据推力方向计算,引入推力方向约束就是为了避免通过推力方向计算的俯仰角过大,ω通过对θ进行差商得到,δ(t) =δd(t) =0。求解上述凸优化问题可以得到一个较好的初值,且计算效率高。仿真部分将比较本初值选取方法和线性初值选取方法对算法1的影响。
3 数值仿真
本节将通过数值仿真来分析类星舰飞行器翻转着陆问题的特性,希望能为相关任务设计提供一定的参考。本节数值仿真主要参考星舰公开的参数[13],部分重要参数见表1。本文在实现算法1 时使用了凸优化求解器ECOS[14]。

表1 飞行器参数Tab.1 Vehicle configurations
飞行器高l= 50 m,lcg= 0.6l,lcp= 0.55l。飞行器初始位置r0=[360 1200]Tm,初始速度v0=[-18.82-106.73]Tm/s,θ0= 170°,ω0= 0(°)/s,m0= 132 t。用于计算的初值θs= 80°,vys=-20 m/s。翻转过程使用3 台发动机,着陆使用2 台发动机。末端位置rf=[0 0]Tm,末端速度vf=[0 -0.1]Tm/s,θf= 90°,ωf=0(°)/s。边界约束中θ(1)max= 170°,θ(1)min= 45°,θ(2)max=105°,θ(2)min= 75°。算 法1 参 数:N1= 40,N2= 50,λvc= 103,λtr= 5 × 10-5,收敛判据ϵvc= 1 × 10-8,ϵtr=1 × 10-8,目标函数中μ=0.3。
使用图4算法求解该算例时,迭代7次收敛,翻转段耗时2.43 s,着陆段耗时13.61 s,整个过程消耗燃料9.773 t。图5 展示了优化结果:图5a 展示了翻转着陆过程的路径点和推力方向。图5b展示了俯仰角和俯仰角速度的变化,最大的俯仰角速度小于给定上界36 。优化的控制量绘制在图5c和图5d中,由于目标函数考虑了让翻转过程高度差较小,所以翻转时先以最大推力和最大摆角加速翻转,接着使用小推力翻转,同时摆角开始减小为接下来减小俯仰角速度做准备,然后在着陆段开始时以最大推力和最小摆角为翻转过程减速,即降低俯仰角速度。整个翻转着陆过程推力几乎是砰—砰(bang-bang)形式,发动机摆角不大于10°。
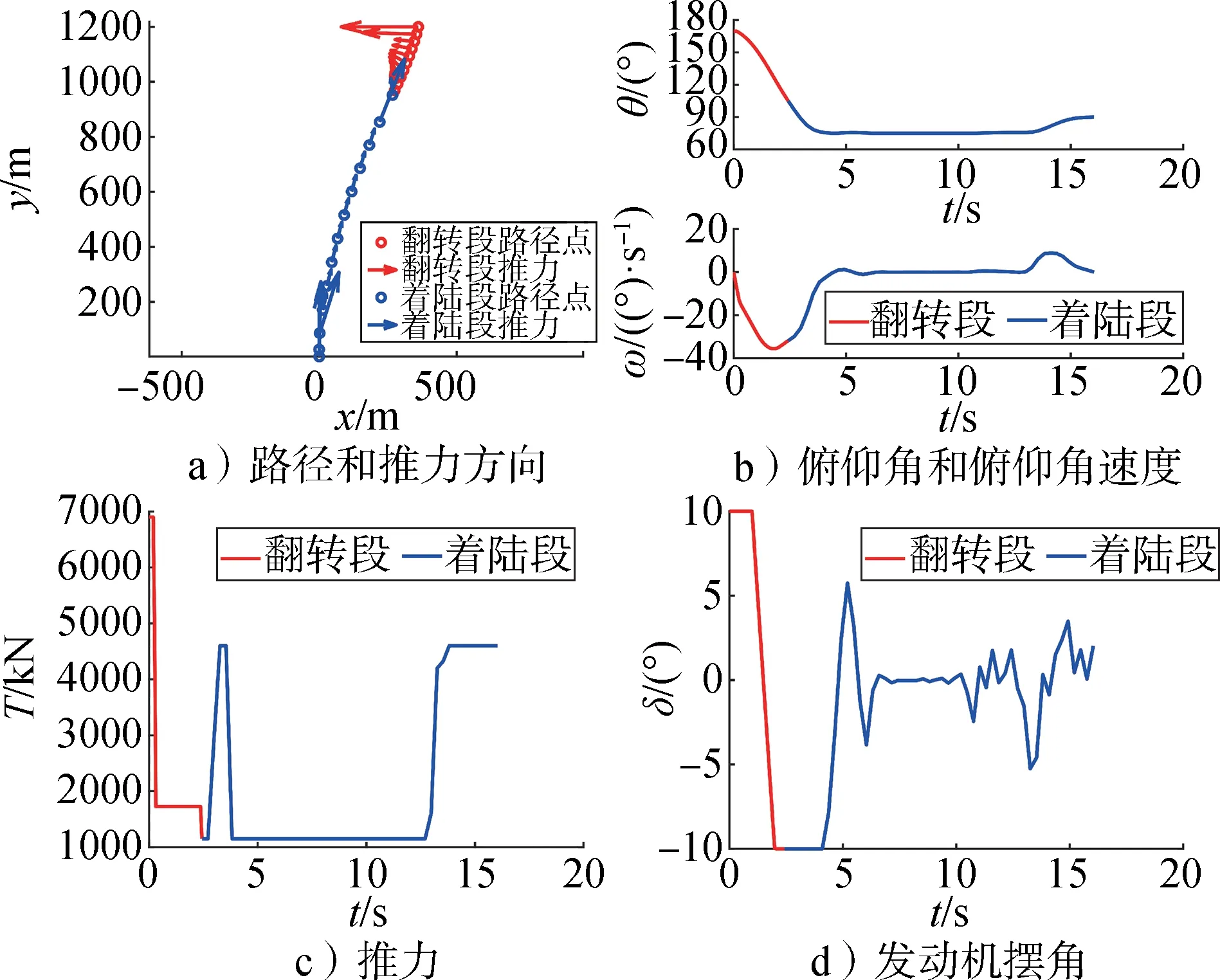
图5 飞行器翻转着陆轨迹优化结果Fig.5 Optimized results of the flipping and landing trajectory of the Starship-like vehicle
接下来改变部分仿真条件,深入研究类星舰飞行器翻转着陆轨迹优化问题的性质,并将对应结果与图5中的结果进行比较。
3.1 不同初值选取方法的影响
对于复杂的轨迹优化问题,初值选取对于序列凸优化算法的收敛性有较大影响。这一小节将比较线性初值和本文初值选取方法对算法1的影响。
使用线性初值,算法1 迭代9 次后收敛,比使用本文初值选取方法多了2次迭代,从图6a可以看出使用本文初值收敛更快。翻转段耗时2.38 s,着陆段耗时14.02 s,整个过程消耗燃料9.947 t,比使用本文初值多消耗174 kg。图6c 展示了推力剖面的对比,使用线性初值时,推力不是砰—砰形式。此外,使用线性初值时,发动机摆角剖面也不如使用本文初值时那么平缓,如图6d所示。大量仿真实例表明算法1使用本文初值选取方法比线性初值收敛性更好,在有些使用线性初值无法收敛的情况下,使用本文初值也能收敛。本文初值选取方法不仅提高了算法的收敛性,而且优化的推力和发动机摆角剖面更适合工程使用。
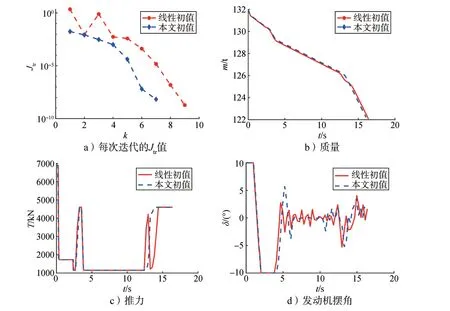
图6 使用线性初值和本文方法确定的初值的结果对比Fig.6 The comparison between the results with linear initial guess or the initial guess obtained by the proposed method
3.2 发动机摆角响应相关约束的作用
在3.1 节中说明了引入发动机摆角响应和相关约束的作用——避免求解的发动机摆角振荡。这一小节将给出不使用发动机摆角响应δd而其它部分都相同时的计算结果。
如前所述,使用δd的算例迭代7 次收敛,而不使用δd的算例迭代20次未收敛。图7给出了使用和不使用δd计算结果的对比(不使用摆角响应的算例20次迭代未收敛,这里画了第20次迭代中的解),图7a和图7c显示两个算例计算的推力和速度剖面几乎相同,但是发动机摆角差别较大,不使用δd的算例得到的发动机摆角(见图7b 中红色实线)着陆前出现了剧烈的振荡。从图7d可以看出不使用δd时,Jtr还未小于ϵtr就不再减小,因此不使用δd的算例没有收敛。发动机摆角剧烈振荡是此算例不好收敛的主要原因。

图7 不使用和使用摆角响应约束求解结果的对比Fig.7 The results solved with and without δd
3.3 着陆使用发动机台数的影响
仿真使用的飞行器的发动机推力较大,足以实现单台发动机着陆。这一小节给出单台发动机和两台发动机着陆时的对比结果。翻转段仍然使用三台发动机。
使用单台和两台发动机着陆的算例都是迭代7次收敛。图8展示了使用单台和两台发动机着陆时优化的控制量,两个算例推力变化趋势相近,两台发动机着陆时大推力持续时间更短。单发动机着陆消耗燃料10.727 t,两台发动机着陆消耗燃料9.773 t,少消耗954 kg燃料。由此可见飞行器的推力设计对其着陆燃料消耗也是有一定影响的。

图8 单台发动机和两台发动机着陆的控制量对比Fig.8 The differences of controls between one-engine landing and two-engine landing
3.4 先翻转再着陆和边翻转边着陆的比较
上文的仿真算例中,目标函数中的惩罚系数μ都取0.3,当目标函数中μ取0时目标函数就变成了最省燃料,因为不考虑对翻转过程高度差的优化,可能出现翻转刚结束飞行器就接近地面的情况,这里把这种优化目标对应的优化问题P0称为边翻转边着陆问题;μ= 0.3 时目标函数表示先翻转再着陆的同时节省燃料,这种优化目标对应的问题P0就是本文主要讨论的先翻转再着陆问题。本节将通过仿真比较两种着陆方式的结果。
先翻转再着陆和边翻转边着陆两个算例都迭代7 次收敛,边翻转边着陆时燃料消耗8.844 t,比先翻转再着陆少消耗929 kg燃料。图9展示了两个算例的仿真结果对比。图9a是飞行器俯仰角和俯仰角速度变化曲线,可以看出边翻转边着陆(μ= 0)时翻转过程变长,翻转过程变慢。图9b 显示了质量变化,边翻转边着陆更省燃料,因为其目标函数就是最省燃料。图9c 和图9d 是两个算例推力和发动机摆角的对比。边翻转边着陆的前期使用最小推力,因为不需要快速翻转;着陆前先最小推力再最大推力。这个边翻转边着陆的算例中翻转段耗时较短,有些算例中边翻转边着陆问题中翻转过程可以占整个飞行时间的一半以上。
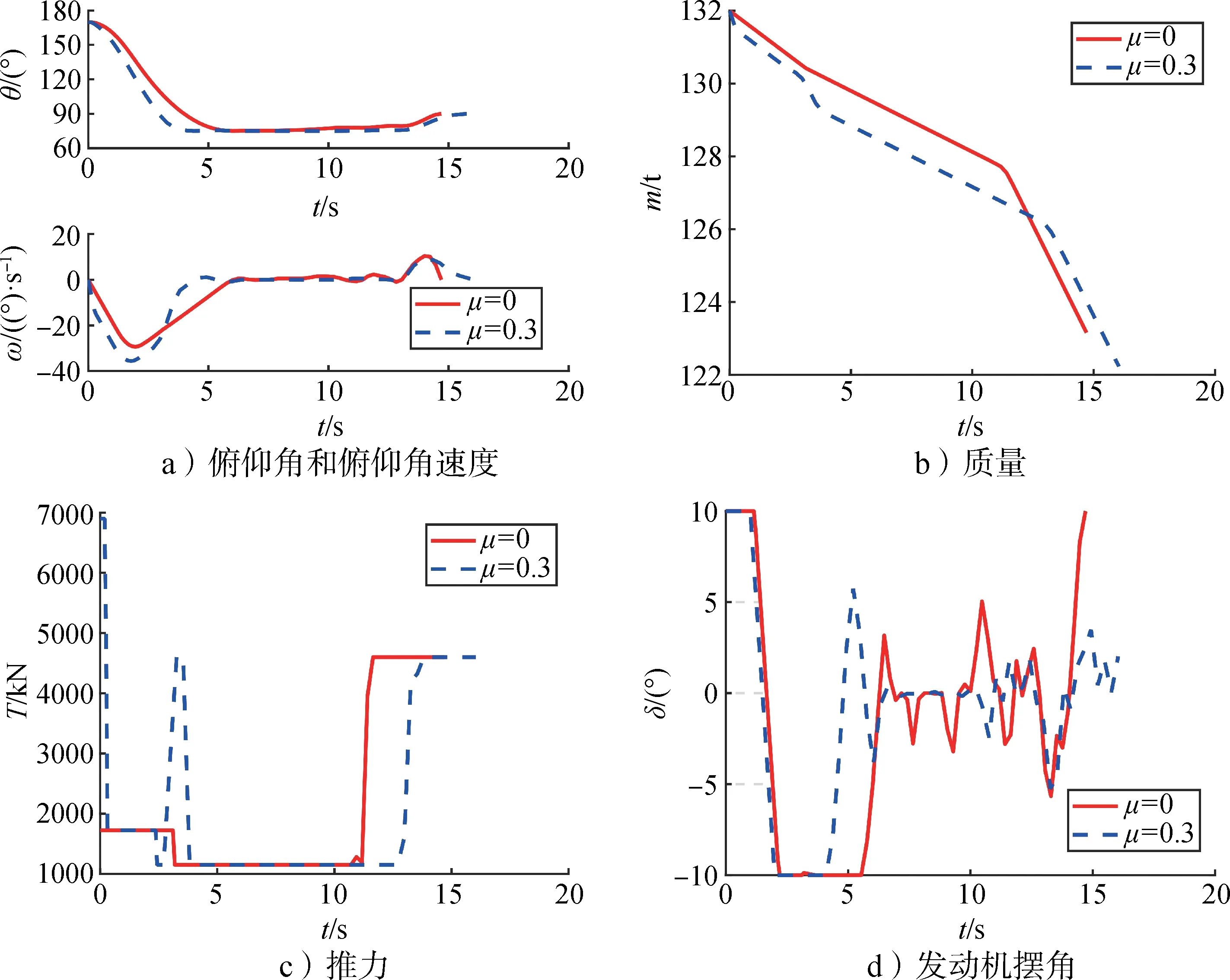
图9 先翻转再着陆和边翻转边着陆的结果对比Fig.9 The comparison between flipping before landing case and flipping while landing case
4 结 论
本文对类星舰飞行器翻转着陆轨迹优化问题进行了建模,设计了用于求解该问题的序列凸优化算法。为了提高算法的收敛性,该算法引入虚拟控制,惩罚信赖域,并给出了较好的初值计算方法。通过数值仿真可以发现,在求解考虑姿态动力学的类星舰飞行器翻转着陆轨迹优化问题这样一个强非线性轨迹优化问题时,与一般的序列凸优化算法相比本文设计的算法收敛性有很大提高。本文给出的翻转着陆过程的轨迹优化结果可以为相关飞行器的研发提供一定的参考。

