不规则波作用下回转体出水过程数值研究

王凡瑜，权晓波，魏海鹏，孔德才

（北京宇航系统工程研究所，北京，100076）

0 引 言

波浪是影响跨介质航行体出水过程载荷、姿态及离散特性的重要环境因素，其影响规律与作用机理受到相关领域学者的广泛关注。姜涛［1］基于Stokes波比较了航行体波峰出水与波谷出水的运动特性；陈世雄［2］研究了波浪相位、攻角以及航行体速度方向对航行体受力特性与空泡溃灭特性的影响；朱坤等［3］同样模拟了航行体在不同相位二阶Stokes波下的出水运动，指出波浪相位通过自由面附近水质点运动速度的大小与方向影响肩空泡对称性，进而影响航行体受力与姿态；周炫成［4］进一步研究了浪级对航行体运动及受力的影响；权晓波等［5］模拟了二阶Stokes波作用下的航行体出水运动，发现航行体所受俯仰力矩与波浪传播方向上航行体前后两侧的不对称旋涡结构有关。

实际环境中波浪通常为不规则波，但目前关于波浪对航行体出水运动的影响研究大多在规则波条件下开展，基于不规则波的研究还十分有限。王亚东等［6］采用P-M谱与SWOP方向分布函数描述不规则波，基于势流理论与切片理论计算波浪力（矩）并代入弹道方程组求解，大量子样的统计分析表明，相关运动参数的最大偏差随浪级或浪向角均近似线性变化，而采用势流方法的局限在于无法考虑流体的黏性作用；王之海等［7］采用ⅠTTC 谱模拟了不规则波作用下的航行体出水运动，但未分析波浪流场影响。

本文基于N-S方程，采用P-M谱，通过边界条件造波法生成了有义波高相等但自由面形态不同的两不规则波，在此基础上模拟了半球头回转体出水运动过程，比较了两不规则波条件下回转体运动特性及受力特性的异同，分析了不规则波流场对回转体运动及受力的影响。

1 数值方法

1.1 控制方程

对常黏性系数牛顿流体的三维不可压缩流动，有连续性方程：

动量方程为

式中ui为速度分量；xi为位矢分量；ρ为密度；p为压强；μ为动力黏性系数；gi为重力加速度分量。

在RANS（Reynolds-Averaged Navier-Stokes）方程框架下，采用k-ωSST模型［8］封闭湍流项，耦合求解连续性方程与动量方程。气水自由面采用VOF 模型［9］模拟。

1.2 不规则波模拟方法

Longuet-Higgins 等［10］提出将不规则波视作大量小幅线性波的叠加，即：

式中η(x1，t)表示t时刻不规则波在水平坐标为x1处的自由面高度；N为成分波的个数；an，kn，ωn，φn分别为第n个成分波的波幅、波数、角频率与相位。

根据P-M 谱［11］确定各成分波的波幅及其他波浪要素。改写P-M 谱表达式，以有义波高Hs为参数［12］，有：

式中S(ω)表示角频率为ω的波浪成分对应的能量密度；α为常值系数，α=8.1×10-3；g为重力加速度。按式（5）计算略去2ε倍波谱总能量的上、下限频率：

式中d为水深。各成分波的相位φn为［0，2π］上均匀分布的随机变量。

采用边界条件法造波，造波边界的相分数条件由式（3）确定，速度条件由各成分波在边界处的速度线性叠加得到，即：

式中Tn为各成分波的周期，Tn= 2π/ωn。

取成分波个数N=200，模拟有义波高Hs=1 m的不规则波，数值结果如图1所示，与规则波相比，不规则波流场呈现出较强无序性。提取自由面高度时间序列反演波谱，如图2 所示，反演谱与目标谱吻合较好，表明所述方法能够可靠地模拟不规则波。

图1 数值波浪流场Fig.1 Flow fields of numerical wave

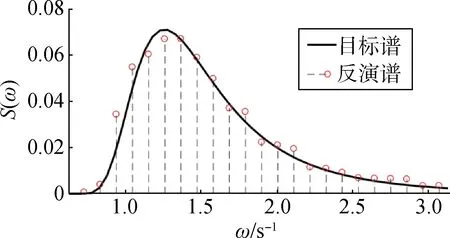
图2 不规则波数值结果反演谱Fig.2 Spectrum retrieved from numerical irregular wave

2 算例设置

本文的研究对象为直径1 m、总长5.5 m的半球头回转体。计算域长30 m，宽10 m，高45 m，其中静水深30 m。X、Y、Z三轴与前述位矢分量xi（i=1，2，3）一一对应，正方向定义一致，即：X轴正方向为波浪传播方向，Y轴正方向竖直向上，Z轴正方向据右手定则确定。如图3 所示，忽略回转体沿Z轴的平动以及偏航、滚转运动，采用半模模拟回转体三自由度出水过程。在t0时刻，回转体顶点距静水面19.5 m，速度30 m/s。不规则波有义波高Hs=1 m。-X面与-Z面设置为速度入口，+X面与+Y面设置为压力出口，+Z面设置为对称面，-Y面与回转体表面设置为无滑移壁面。

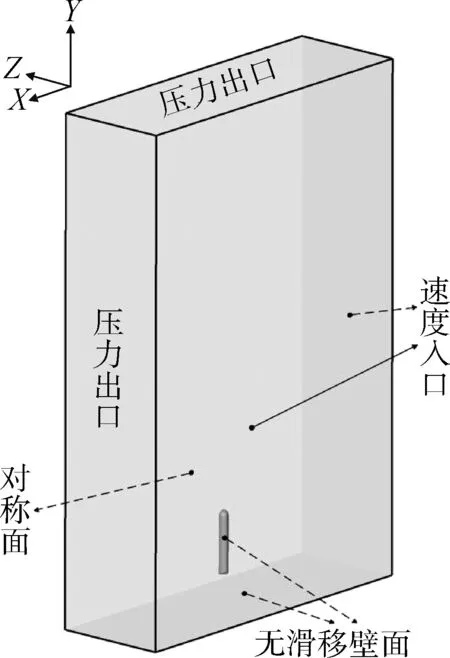
图3 计算域示意Fig.3 Skeleton of computational domain

3 结果与分析

本文分别在两种不规则波条件下开展了回转体出水过程数值模拟，两条件仅成分波相位不同，相位由程序在［0，2π］上随机生成。回转体出水位置附近的自由面形态如图4所示。

图4 自由面形态Fig.4 Free surface profiles

3.1 回转体运动特性

回转体运动特性如图5所示。

图5 回转体运动特性Fig.5 Kinetic profiles

不规则波算例及无波浪对照算例的回转体质心运动轨迹如图5a所示，其中Y轴原点位于静水面处。可以看出，回转体质心位于静水面9 m以下时，不规则波作用下的质心运动轨迹与无波浪状态几乎重合；回转体运动至质心距静水面不足9 m时，不规则波作用下的质心运动轨迹显著偏离无波浪状态，且两不规则波算例中偏离方向相反。

图5b给出了各算例中回转体质心X方向位移的时历曲线。在（t0+0.5）s 前，不规则波作用下的质心X方向位移与无波浪状态没有明显差异；自（t0+0.5）s起，不规则波作用下的回转体质心X方向位移显著偏离无波浪状态，且不规则波算例2中偏离程度高于不规则波算例1。

如图5c所示，不规则波作用下的回转体质心Y方向位移时历曲线与无波浪状态近似重合。由放大图可知，同一时刻，无波浪状态下质心Y方向位移最大，不规则波算例1 次之，不规则波算例2 最小。说明不规则波作用下回转体Y方向速度略微衰减，且不规则波算例2中衰减稍大于不规则波算例1。

各算例中回转体俯仰角时历曲线如图5d 所示。（t0+0.15）s前，各算例俯仰角时历曲线未见明显差异。自（t0+0.15）s起，不规则波作用下的回转体俯仰姿态显著偏离无波浪状态：不规则波算例1中回转体做正向俯仰运动；不规则波算例2中回转体做负向俯仰运动，且俯仰姿态的量值高于不规则波算例1。

综上所述，不规则波主要影响回转体的质心X方向运动与俯仰姿态，对质心Y方向运动影响较小。在所模拟的两不规则波作用下，回转体质心X方向位移方向相反、量值差异较大，俯仰姿态亦然。

3.2 回转体受力特性

如图6所示定义半球头回转体的头部、柱段中部及柱段尾部，分别计算各部段所受法向力与俯仰力矩。

图6 回转体部段分界Fig.6 Segment definitions

不规则波算例1中半球头回转体受力特性如图7所示。由图7可知，回转体头部先受量值较小的负向法向力及俯仰力矩。随着回转体向上运动，头部所受法向力及俯仰力矩逐渐变正，量值显著增大，直至出水阶段迅速减小。柱段中部所受法向力较大，但因在质心上下两侧的分布接近对称，产生的俯仰力矩反而较小；出水阶段法向力分布偏向质心下方，故产生较大的负向俯仰力矩。柱段尾部先受量值逐渐增大的负向法向力，在（t0+0.4）s 左右达峰值后逐渐减小，约在（t0+0.6）s时转为正向并逐渐增大，直至出水阶段缓慢减小。

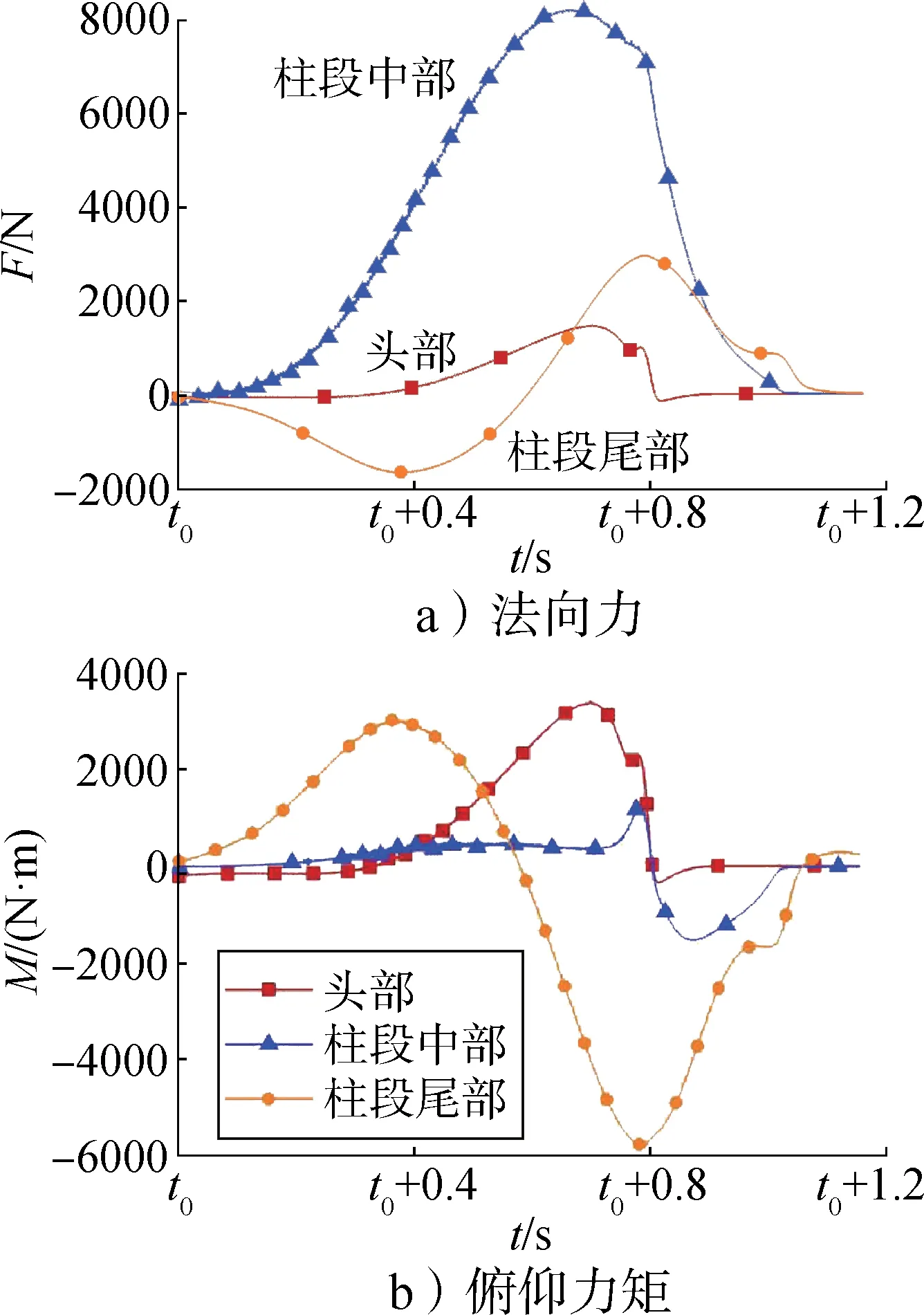
图7 不规则波算例1中回转体受力特性Fig.7 Dynamic profiles in 1st irregular wave simulation

如图8所示，不规则波算例2中半球头回转体受力特性与不规则波算例1类似：头部所受法向力及俯仰力矩改变方向后量值显著增大，在出水阶段迅速减小；柱段中部所受法向力较大，但仅在出水阶段产生较大的俯仰力矩；柱段尾部所受法向力及俯仰力矩先增大后减小，反向后再增大，直至出水阶段缓慢减小。

图8 不规则波算例2中回转体受力特性Fig.8 Dynamic profiles in 2nd irregular wave simulation

两不规则波算例中半球头回转体受力特性主要有两点差异：a）回转体各部段所受法向力方向相反、所受俯仰力矩方向相反，导致两算例中回转体质心X方向位移方向相反、俯仰姿态方向相反；b）不规则波算例2中回转体所受法向力及俯仰力矩的量值显著高于不规则波算例1，导致不规则波算例2中回转体质心X方向位移及俯仰姿态的量值高于不规则波算例1。

3.3 不规则波流场影响

a）从自由面形态（见图4）可知，不规则波算例1 中，回转体在由波峰向波谷发展（简称“峰-谷”）的波浪条件下做出水运动，而不规则波算例2中条件为由波谷向波峰发展（简称“谷-峰”）。对线性波，峰-谷条件与谷-峰条件相位相反，同一位置水质点运动方向相反。不规则波与此类似，峰-谷条件下水质点运动对回转体的作用与谷-峰条件相反，故两算例中回转体质心X方向位移方向相反、俯仰姿态方向相反。

此外，不规则波算例2中回转体遭遇的波峰波谷高度差大于不规则波算例1，说明不规则波算例2 中回转体遭遇的波浪能量较强，所以不规则波算例2中回转体受到较大的法向力与俯仰力矩，进而导致质心X方向位移与俯仰姿态的量值较高。

b）回转体头部受力（矩）方向先后由波浪速度场和回转体俯仰姿态决定。如图9a所示，对不规则波算例1，在t0时刻，回转体俯仰角较小，头部附近压力场较对称，但波浪场水平速度沿X轴负方向，诱导头部产生负法向力，使回转体头部受负俯仰力矩；如图9b所示，在（t0+0.7）s时，回转体有较大的正向俯仰角，-X侧表面迎流，头柱交界处低压区小于+X侧，法向力指向+X侧，形成正俯仰力矩。

图9 头部附近压力云图Fig.9 Pressure contours near head

相反地，如图9c、9d 所示，不规则波算例2 中，t0时刻波浪速度场诱导回转体头部受正俯仰力矩；在（t0+0.7）s时，回转体俯仰姿态为负，+X侧表面迎流，头柱交界处低压区小于-X侧，法向力指向-X侧，产生负俯仰力矩。

综上所述，回转体俯仰角较小时，回转体头部受力（矩）方向由波浪速度场主导；随回转体俯仰角量值增大，头部受力（矩）方向逐渐转为由俯仰姿态主导。

c）回转体柱段尾部受力（矩）方向与底部低压区密切相关。如图10a 所示，不规则波算例1 中，在（t0+0.4）s 时刻，回转体底部-X侧低压区大于+X侧，柱段尾部+X侧表面压力较高，法向力指向-X侧，形成正向俯仰力矩；如图10b所示，在（t0+0.7）s时刻，底部低压区变为+X侧较大、-X侧较小，此时柱段尾部-X侧表面压力较高，产生负向俯仰力矩。

图10 尾部附近压力云图Fig.10 Pressure contours near tail

不规则波算例2 与此类似：如图10c、10d 所示，在（t0+0.4）s与（t0+0.7）s时刻，回转体底部低压区相对大小相反，柱段尾部表面压力差方向相反，使所受法向力方向相反、俯仰力矩方向相反。

综上，回转体出水过程中柱段尾部受力（矩）方向发生变化，底部低压区相对大小亦发生变化。

4 结 论

本文基于P-M谱生成了有义波高相等但自由面形态不同的两不规则波，在此基础上模拟了半球头回转体三自由度出水过程，提取了回转体运动参数，分阶段计算了回转体所受法向力与俯仰力矩，分析了不规则波对回转体受力特性与运动特性的影响，得到以下结论：

a）峰-谷条件与谷-峰条件下，不规则波流场中水质点对回转体作用方向相反，使回转体各部段所受法向力方向相反、俯仰力矩方向相反，导致回转体质心水平运动方向相反、俯仰姿态方向相反。

b）有义波高相等的不规则波作用下，回转体遭遇的波峰波谷高度差越大，所受法向力与俯仰力矩的量值越高，质心X方向运动与俯仰姿态偏离无波浪状态越显著。

c）回转体俯仰角较小时，头部受力（矩）方向由波浪速度场主导，随后逐渐转为由俯仰姿态主导。