基于特征投影矩阵和线性约束的水声阵列信号抗主瓣干扰方法
王凯玥,王景景,闻卫军
(青岛科技大学 信息科学技术学院,山东 青岛 266061)
基于水下阵列的水声信号波束形成[1]方法是一种空间滤波器,通过将换能器在空间上按一定形状排列组成水下阵列,通常被用作水声通信的发送或者接收设备。其中应用最广泛的是最小方差无畸变响应[2](minimum variance distortionless response,MVDR)波束形成器,通过限制波束能量输出,同时约束期望信号方向响应为1,获得最大输出信干噪比。然而复杂海洋噪声环境下,干扰和噪声的种类繁多,根据干扰源射入水声阵列位置的不同,可以分为主瓣干扰和旁瓣干扰。当存在多个已知干扰位置的旁瓣干扰源时,线性约束最小方差[3](linearly constrained minimum variance,LCMV)波束形成器,可约束干扰源位置波束能量输出,降低对干扰的接收性能,从而抑制干扰。然而当干扰落入阵列方向图主瓣时,常规的波束形成算法会导致主瓣畸变、旁瓣电平抬高以及输出信干噪比降低等问题。
目前,常用的主瓣干扰抑制算法分为两类,一类是基于阻塞矩阵预处理(blocking matrix preprocessing,BMP)的主瓣干扰抑制方法,一类是基于特征投影矩阵预处理(eigen-projection matrix preprocessing,EMP)的主瓣干扰抑制方法。YU 等[4]首次提到阻塞矩阵的概念,文献[5]在此基础上提出了基于BMP 的主瓣干扰抑制方法,利用先验已知的主瓣干扰方位信息构造阻塞矩阵滤除主瓣干扰,且不影响后续自适应波束形成对旁瓣干扰零陷的形成。但是BMP 算法损失了一个天线单元的自由度,而且对主瓣干扰角度的预测精度要求较高,在实际中很难达到。为进一步提高对主瓣干扰的抑制能力,文献[6]提出了基于EMP 的主瓣干扰抑制算法,该方法不需要提前知道主瓣干扰的入射角度,但是存在主波束峰值偏移的问题。文献[7]提出了基于特征投影预处理和协方差矩阵重构(eigen-projection matrix preprocessing and covariance matrix reconstruction,EMP-CMR)的方法,该方法通过相关系数法确定了主瓣干扰对应的特征矢量,避免了EMP方法中标量因子不易确定的问题,并在预处理的同时通过重构协方差矩阵求取了权矢量,修正了EMP方法中的峰值偏移。但是在实际中,协方差矩阵难以得到,通常用采样协方差矩阵(sampling covariance matrix,SCM)代替,而上述方法均是在采样数据中不包括期望信号的基础上进行研究的,当采样数据中混入期望信号,阵列方向图会产生主瓣偏移问题。此外,EMP及其改进算法仅限于主瓣干扰强度较小,与旁瓣干扰信号差异大的情况,而水声阵列信号主要面临着强干扰、弱目标的问题,当主瓣干扰强度较大时,各个特征向量对其余方向的导向矢量贡献不为零[8],利用上述协方差矩阵求取自适应权矢量会导致波束形成在旁瓣零陷变浅甚至不产生零陷。
针对上述问题,本工作在EMP方法的基础上,提出了基于特征投影矩阵和线性约束的(EMP-LC,eigen-projection matrix preprocessing and linear constraints)的水声阵列信号抗主瓣干扰方法。仿真实验结果表明,本工作算法有效抑制了主旁瓣干扰的同时使得主波束保形,获得了较高的输出信干噪比。
1 水声阵列信号接收模型
采用M个阵元等间距排列而成的均匀线阵作为水声信号的接收阵列,如图1所示。
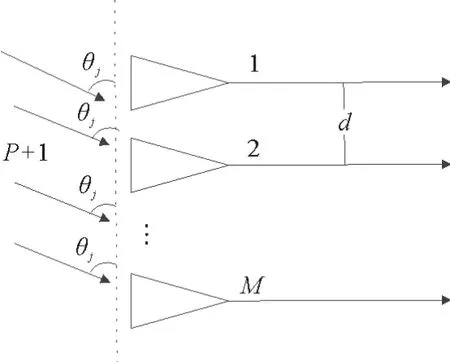
图1 水声阵列信号接收图Fig.1 Diagram of underwater acoustic array signal receiving model
假设1个期望信号和P个干扰(1个主瓣干扰,P-1个旁瓣干扰)从远场以平面波入射到阵列上,且满足P+1<M,各通道噪声为彼此独立的加性噪声。期望信号、干扰信号和噪声互相独立,则水声阵列t时刻的接收信号为
其中水声阵列接收信号X(t)是(P+1)×1 维向量,阵列流形矩阵表示为,d=λ/2为阵元间距,λ为信号波长,a(θ0)表示期望信号的导向矢量,θ0表示期望信号的到达方位信息,a(θj),(j=1,…,P)表示第j个干扰的导向矢量,θj,(j=1,…,P)表示第j个干扰信号的到达方位信息。S(t)=[s0(t),s1(t),…,sP(t)]T为入射信号的复包络,s0(t)表示目标信号复包络,sj(t)(j=1,…,P)表示第j个干扰复包络,N(t)表示各阵元处加性噪声。理想中的协方差矩阵可以表示为
其中,qj表示第j个信号的功率为噪声的功率,I为单位矩阵,()H为共轭转置。在实际中无法精确得到R,所以常采用SCM 对接收信号的协方差矩阵进行估计:
其中K为快拍次数。MVDR 波束形成器根据最大信干噪比准则,可得最优自适应权矢量为
其可以自适应地使阵列输出在期望方向上功率最小同时信干噪比最大,即抑制旁瓣干扰和噪声。
2 传统特征投影矩阵预处理类算法
2.1 基于特征投影矩阵(EMP)的主瓣干扰抑制算法
EMP算法假设了采样数据没有混入期望信号,该算法首先对采样协方差矩阵进行特征值分解:
其中,λj是协方差矩阵的第j个特征值,uj是协方差矩阵的第j个特征矢量,其中λj按降序排列λ1≥λ2≥…λP≥λP+1≥…λM,Us=(u1,u2,…,uP)和Un=(uP+1,uP+2,…,uM)分别是协方差矩阵的特征矢量张成的干扰子空间和噪声子空间,Λs和Λn分别是干扰和噪声对应的特征值对角阵。
主瓣干扰对应的特征矢量可以利用下式确定um:
其中c是一个标量,它在实际应用中不易确定。确定主瓣干扰对应的特征矢量um后,构造特征投影矩阵:
其中I是单位矩阵。利用特征投影矩阵对阵列接收数据X进行预处理:
其中(t)=Bn(t)是接收数据经过预处理后的噪声。由于主瓣干扰对应的特征矢量um与其他旁瓣干扰的导向矢量正交,所以得到:
故经过预处理后的信号是:
通过式(10)可以看出,接收数据经过特征投影矩阵预处理后,消除了主瓣干扰成分,接下来再进行自适应波束形成则不会导致主瓣畸变。但是式(6)中的c不易确定,而且由于预处理中存在特征投影矩阵B,会导致利用MVDR 算法波束形成时产生主瓣偏移。
2.2 基于特征投影矩阵和协方差矩阵重构(EMPCMR)的主瓣干扰抑制算法
针对上述问题,文献[7]在假设采样数据中不包含期望信号的条件下,提出了基于EMP-CMR 的主瓣干扰抑制方法,具体算法流程如图2所示。
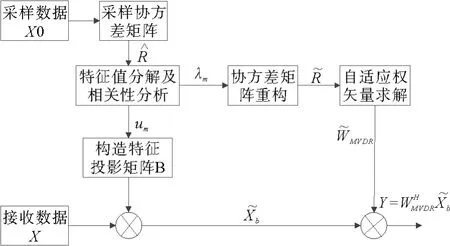
图2 EMP-CMR算法流程图Fig.2 Flow chart of EMP-CMR algorithm
该算法首先改进了主瓣干扰特征矢量的判别方法。根据波束指向的导向矢量a(θ0)和干扰的特征矢量uj,(j=1,…,P)之间的相关性,确定主瓣干扰的特征值和特征矢量,避免了EMP算法中标量c的选择问题。两个向量之间的相关系数通常定义为
其中‖·‖表示求模运算。因为主瓣干扰位于主波束内,所以主瓣干扰的特征矢量与主波束指向即期望信号导向矢量的相关性最大,可以表示为
其中um为主瓣干扰对应的特征矢量。
其中U=[Us,Un],为重构后的特征值矩阵:
利用重构后的协方差矩阵求取权矢量,对预处理后的接收数据进行波束形成可得到理想的波束响应图。但是,当采样数据混入期望信号且主瓣干扰功率较大时,上述方法会产生峰值偏移,旁瓣电平升高、零陷消失等问题。
3 基于特征投影矩阵和线性约束(EMP-LC)的水声阵列信号抗主瓣干扰算法
当采样数据没有混入期望信号时,EMP算法可以有效地抑制主瓣干扰,但是该算法会产生主波束指向偏移问题,EMP-CMR 算法在保留了EMP 算法消除主瓣干扰效果的基础上,修正了主波束偏移。但在实际中,采样数据中难免会混入期望信号,而且在复杂的海洋环境中干扰强度较大,当主瓣干扰强度较大时,会导致预处理后的数据在后续波束形成时对旁瓣干扰的抑制作用减弱,上述算法均会出现峰值偏移、旁瓣零陷变浅等问题。因此,本工作在EMP算法的基础上提出了基于EMP-LC的水声阵列信号抗主瓣干扰方法。具体算法流程如图3所示。
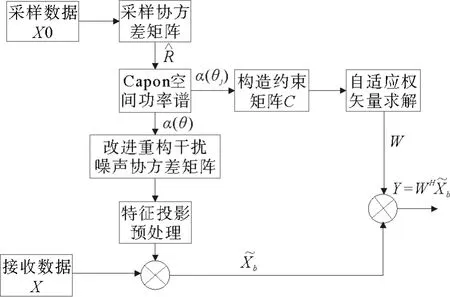
图3 所提算法流程图Fig.3 Processing block diagram of the proposed algorithm
3.1 改进重构干扰噪声协方差矩阵
首先,重构干扰噪声协方差矩阵,使其不包含期望信号。空间中任意位置的Capon空间功率谱可以表示为
对于任意一个角度对应的矢量a(θ),其对应的空间功率谱为P(θ)。文献[14]假设期望信号的角度区域为Θ表示整个空间中非期望信号区域部分,包括了所有的干扰和噪声,利用Capon空间功率谱重构了干扰噪声协方差矩阵:
但本工作利用干扰噪声协方差矩阵是为了对其进行特征值分解,筛选出主瓣干扰对应的特征矢量,构造特征投影矩阵以消除主瓣干扰,因此本工作对式(17)的积分区域进行了改进。
根据Capon空间功率谱,可以估计出的干扰角度θi,(i=1,2,…,P),但由于估计误差的存在,真实的干扰角度在θi附近,所以为每个干扰角度选取合适的区间范围ΘPi(i=1,2,…,P)。那么,所有干扰信号附近区域的集合可以表示为
3.2 特征投影预处理
对新重构的干扰噪声协方差矩阵进行特征值分解:
其中表示主瓣干扰的特征矢量,由它张成了主瓣干扰子空间,构造特征投影矩阵:
对接收数据进行预处理,消除主瓣干扰成分:
3.3 线性约束波束形成
通过特征投影矩阵预处理消除了数据中的主瓣干扰成分,但依然存在旁瓣干扰,因此,需要进一步求取自适应权矢量进行波束形成,抑制旁瓣干扰。但是当主瓣干扰功率较大时,接收数据经过预处理会导致后续波束形成在旁瓣干扰处的零陷变浅,对旁瓣干扰的抑制作用减弱。因此,本工作通过添加线性约束条件,构造期望信号和旁瓣干扰子空间的约束矩阵,保证期望信号方向增益的同时使旁瓣干扰置零,在等式约束的条件下最小化权矢量的模,消除噪声子空间抖动的影响,增强在主瓣干扰强度较大时波束形成对旁瓣干扰的抑制作用。由此得到式(25)约束优化问题:
其中,C=[a(θ0),a(θj)],(j=1,…,P-1),g=表示期望信号的导向矢量,a(θj)表示P-1个旁瓣干扰的导向矢量,旁瓣干扰的角度由Capon空间谱估计法得到。
应用拉格朗日乘子法,由式(25)构造代价函数:
对代价函数求对W的梯度并令之为零,即
将其带入CHW=g得:
将式(29)带入式(28)得:
因此,EMP-LC算法的输出信号为
4 实验仿真与分析
本工作使用16个阵元等距均匀线阵作为水下接收阵列半波距离摆放,阵元均为各向同性阵元。正交相移健控(quadrature phase shift key,QPSK)信号是一种水声通信系统中常用的信号,因此采用QPSK 信号作为期望信号和干扰信号,噪声为加性高斯白噪声。期望信号的频率为10 kHz,入射角度为0°,远场处分布了三个频率分别为12、13、14 kHz的非相干干扰信号,干噪比分别为20、30、40 dB,干扰源的入射角度分别为3°、-25°、30°。具体如表1所示。

表1 仿真环境参数Table 1 Simulation environment parameters
图4是利用Capon空间功率谱估计法得到的,纵轴表示阵列输出的平均功率,横轴表示角度,如果某个方向有信号,则输出信号的平均功率较高,如果没有信号只有噪声,则输出噪声的平均功率。如图4可知,-25°,3°和30°处信号功率较高,对应了干扰信号的角度,其中最接近来波方向0°的是主瓣干扰的角度。
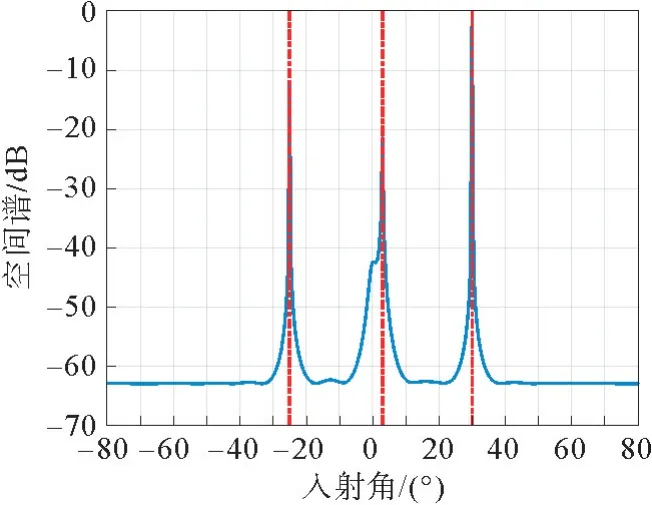
图4 空间功率谱图Fig.4 Diagram of space power spectrum
4.1 采样数据中是否含有期望信号的阵列响应图
当采样数据中混入期望信号时,会导致EMP算法和EMP-CMR 算法对主瓣干扰的特征矢量筛选错误,且对消部分期望信号,阵列方向响应图的主瓣产生偏移现象,因此本实验仿真了EMP 算法、EMP-CMR 算法和所提算法在采样数据是否混入期望信号的情况下的阵列方向响应图,见图5、图6。
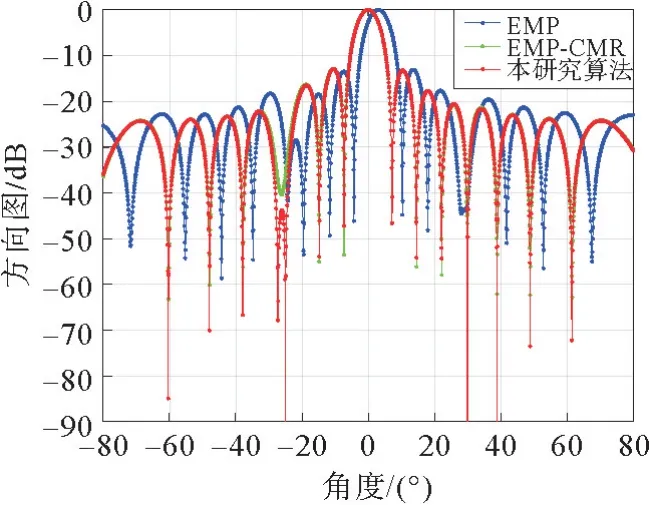
图5 采样数据中不包含期望信号Fig.5 Sample data does not contain the desired signal
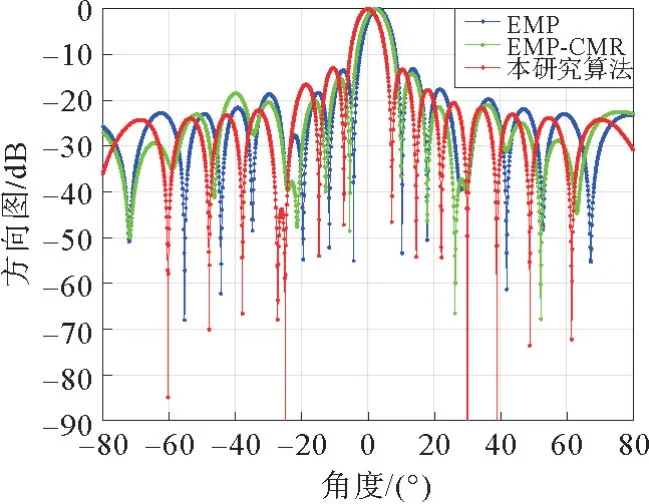
图6 采样数据中包含期望信号Fig.6 Sample data contain the desired signal
由图5可以看出,在采样数据中不包含期望信号的情况下,EMP 算法虽然消除了主瓣干扰,未在主瓣内形成零陷,但是存在峰值偏移问题,EMPCMR 算法和所提算法都能在消除主瓣干扰的同时使得主波束指向期望信号方向。由图6可以看出,在采样数据中包含期望信号的情况下,EMP算法和EMP-CMR算法都存在主瓣峰值偏移现象,这是因为采样数据中混入的期望信号被当成干扰对消了部分能量。而所提算法的主波束未发生偏移,这是因为本工作改进重构了干扰噪声协方差矩阵,剔除了期望信号的影响。在旁瓣干扰的抑制方面,通过对比图5和图6可以看出,在旁瓣干扰-25°处EMP算法和EMP-CMR 算法大约可形成-40~-50 dB的零陷,而所提算法可形成-90 dB的零陷,说明所提算法在未知采样数据是否混入期望信号的情况下均对旁瓣干扰有良好的抑制效果。
4.2 不同主瓣干扰功率的阵列响应图
当主瓣干扰强度较大时,会减弱EMP 算法和EMP-CMR 算法后续波束形成时对旁瓣干扰的抑制,在旁瓣干扰处的零陷变浅。因此,本实验仿真了在采样数据未混入期望信号的情况下,EMP 算法、EMP-CMR 算法和所提算法在主瓣干扰强度不同时的阵列方向图和静态方向图的对比,见图7和图8。
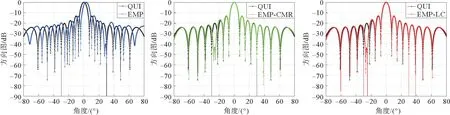
图7 3种算法在主瓣干扰功率为10 dB情况下的阵列响应图Fig.7 Array response diagram of three algorithms in the case of main sidelobe interference power difference of 10 dB
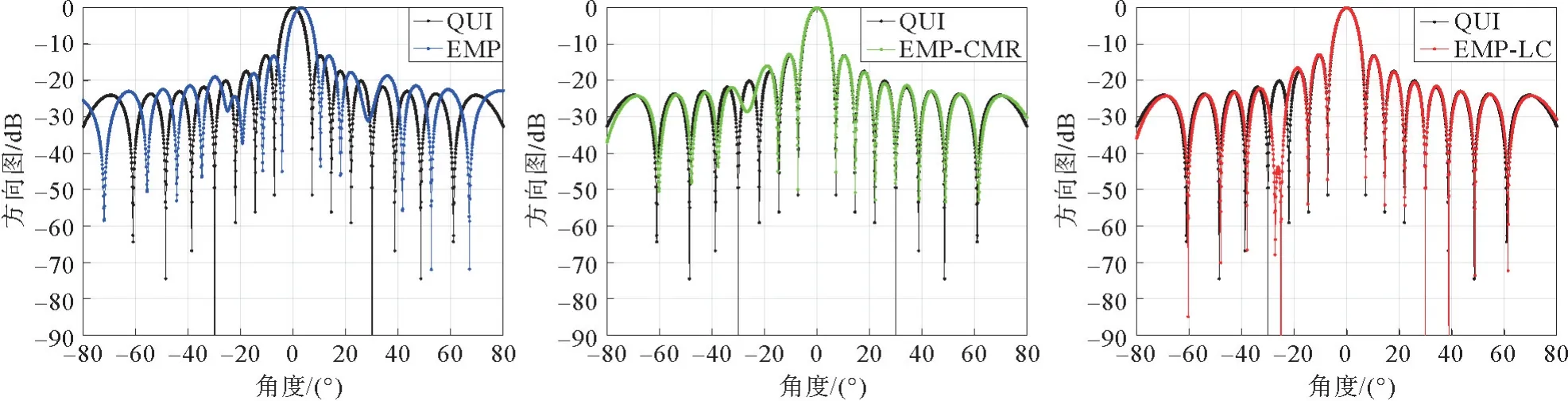
图8 3种算法在主瓣干扰功率35 dB情况下的阵列响应图Fig.8 Array response diagram of three algorithms in the case of main sidelobe interference power difference of 35 dB
由图7可以看出,在主瓣干扰功率为10 dB时,EMP算法、EMP-CMR 算法对旁瓣干扰均有较好的抑制效果,在旁瓣干扰-25°处可形成约-50~-70 dB的零陷。由图8可以看出,当主瓣干扰功率增大为35 dB 时,EMP 算法和EMP-CMR 算法在旁瓣干扰-25°处的零陷变浅甚至消失,这是因为主瓣干扰强度变大时,由于各个特征向量对其余方向的导向矢量贡献不为零,前两者算法的接收数据经过预处理再进行波束形成时,减弱了对旁瓣干扰的抑制。而所提算法通过添加约束条件,使得旁瓣干扰方向置零,在主瓣干扰强度变大后仍对旁瓣干扰有良好的抑制效果,可形成-90 dB的零陷,其余波束逼近静态方向图。
4.3 采样点数对输出信干噪比的影响
实验仿真了在主瓣干扰强度为35 dB,采样点数混入了期望信号的情况下,采样点数在10~100范围内,EMP 算法、EMP-CMR 算法和所提算法的阵列输出信干噪比。
图9 仿真对比了EMP 算法、EMP-CMR 算法和所提算法在采样点数10~100范围内的阵列输出信干噪比。3种算法中,EMP算法的输出信干噪比最低,因为预处理后EMP算法的主瓣峰值偏移,而EMP-CMR 算法通过重构协方差矩阵修正了权矢量,改善了主波束指向偏移的问题。所提算法使用改进重构的干扰噪声协方差矩阵,消除了期望信号的影响,在低采样点下获得了较高的阵列输出。此外所提算法还通过添加线性约束,加深了旁瓣干扰处的零陷,加强了对旁瓣干扰的抑制,相较于EMPCMR 算法提升了1~2.5 dB,有更高的输出信干噪比。
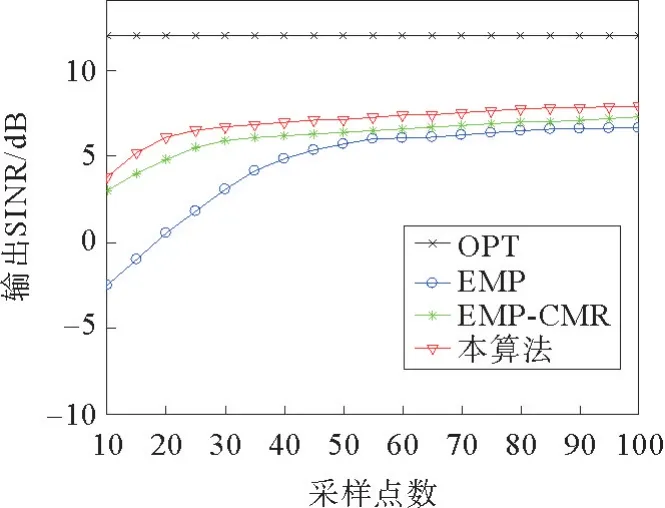
图9 不同采样点数下的输出信干噪比Fig.9 Output signal-to-interference-noise ratio under different sampling points
5 结语
提出了一种基于特征投影矩阵和线性约束的水声阵列信号抗主瓣干扰方法,通过改进重构干扰噪声协方差矩阵,防止主瓣干扰特征矢量筛选错误,构造特征投影矩阵消除主瓣干扰成分。通过添加线性约束条件,构造期望信号和旁瓣子空间的等式约束,保证期望信号增益的同时使旁瓣干扰置零,解决了主瓣干扰强度较大导致后续波束形成的旁瓣零陷变浅问题,在上述约束下使得权矢量的模最小,消除噪声扰动,修正了峰值偏移。仿真结果表明,本算法在有效抑制主旁瓣干扰的同时使得主波束保形,系统输出有更高的信干噪比。

