农村配电网技术线损评估模型研究

王壮壮

（辽宁煤炭基本建设技工学校）

0 引言

在我国的农村地区，由于配电网线路的覆盖范围广、结构复杂且设备较多，导致数据采集变得困难，从而使得精确计算农村配电网技术线损变得异常困难。然而，随着计算机技术和人工智能的不断发展，为农村配电网技术线损计算提供了新的解决思路。目前，很多农村配电网的线损计算方法使用传统的BP（反向传播）神经网络模型，然而这种模型存在一些问题，如效率低下、容易陷入局部最小值等。

虽然当前对BP 神经网络模型进行了一些优化，但其效率仍然不理想。与BP 神经网络模型相比，径向基函数神经网络模型在精确度方面表现出更好的性能，并能更接近全局逼近的水平，从而极大改善了BP 神经网络模型在局部最优解方面的缺陷。此外，在学习效率方面，BP神经网络模型具有固定的速度，收敛速度较慢，训练时间较长。而径向基函数神经网络模型则恰恰相反，收敛速度较快，是一种高效的神经网络模型。因此，在农村配电网技术线损计算中，考虑到线损数据的复杂非线性关系，径向基函数神经网络模型比BP 神经网络模型更为适合，具备逼近任意函数的能力，可应用于农村配电网技术线损的准确计算中。

1 配电网技术线损的定义与构成

在农村配电网技术线损特征评估过程中，首先要关注的是线损变化的影响因素。在本文，笔者主要研究的是技术线损，受农村配电网络自身特征所限制，其设备繁多、结构复杂、分支较多，且智能化水平不高，在获取相关运行数据的时候是比较难的。在分析好电网线损的主要构成的前提下，我们可以获得技术线损、管理线损的比重情况，有助于降低农村配电网线损。所谓电力网线损，主要是指在电能从发电厂到用电户过程中所产生的能力损耗，这一损耗原因较为复杂，可以分为下面几个类别。

在农村配电网技术线损特征评估过程中，首先需要关注线损变化的影响因素。对于农村配电网，由于其设备众多、结构复杂、分支较多，且智能化水平相对较低，获取相关运行数据非常困难。在充分分析电网线损的主要组成部分的基础上，可以了解技术线损和管理线损的比重情况，有助于降低农村配电网的线损。电力网线损主要是指电能从发电厂到用电户过程中所产生的能力损耗。这种损耗的原因非常复杂，可以分为以下几个类别。

（1）技术线损

技术线损，也被称为理论线损，是电网运行中难以避免的电能损耗，通过电网运行数据和结构数据，可以获得技术线损的情况。在技术线损中，电阻损耗和励磁损耗是主要原因。电阻损耗是由于电网设备内部的电阻导致电流流过时产生的能量损耗。励磁损耗则是由于某些电气设备在运行中需要消耗电能来产生自身磁场而造成的能量损耗。

（2）管理线损

在电网运行中，因为管理原因导致电能损失为管理线损，其中有抄表误差、电晕损耗、窃电行为、设备漏电及线路损坏导致的漏电等。在电网运行过程中，可以精确测算出配电网中技术线损所占比重，从而确定管理线损的比重情况，通过降低线损达到降低管理线损的目的。

（3）统计线损

线损是由技术线损和管理线损构成的，表示发电量与售电量之间的差额。对于电网而言，线损率是评估电能损耗情况的重要指标，统计线损率有助于了解损耗情况，从而降低线损。根据线损产生的原因，线损主要可分为固定损耗、可变损耗和不明损耗三种。固定损耗包括配电变压器的铁损和维持设备运行所需的磁能损耗，在电压水平一致时是固定的。可变损耗是随着电流变化而变化的电能损耗，包括线路损耗、电阻损耗、配电变压器的铜损耗以及各种计量设备的铜损耗。

2 配电网技术线损计算方法

传统配电网中，有多种方法可以计算技术线损，包括均方根电流法、回归分析法、等效电阻法和损失系数法。这些计算方法有着不同的使用途径，在计算过程中需要使用的系数。使用范围均有所区别。简言之，不同的计算方法适用于不同的情况和要求。

2.1 均方根电流法

均方根电流法是一种用于计算线路损耗的方法，在线路中通过的均方根电流、电气元件上的电阻数据是其掌握的前提。我们用R 表示在电气元气中的电阻， 通过次元件电流每小时测量值为I1，I2，I3，………I24，则该元件一天内产生的电能损耗∆A为：

式中，∆A表示一天内电能损耗，R表示电气元件的电阻，、、…、表示逐小时测量的电流值。这个公式可以用来计算线路上电气元件一天内的电能损耗。式中的Irms为日均方根电流，它的计算公式为：

如果可以测量无功功率、有功功率和线路线电压，则日均方根电流的计算方法为：

式中，Pi为经过该元件的三项有功功率；Qi为经过该元件的三项无功功率；Ui为该元件两端的电压值。

2.2 等值电阻法

由于使用均方根电流法在配电网技术线损计算中存在一些局限性，由于农村配电网结构复杂、设备繁多等特点。在其获取数据的过程中，每个节点的数据都是难以精准的，这也导致计算准确度大大降低了。此外，在计算左右节点的过程中，数据相加涉及到较大的计算量，增加了计算的复杂性和时间成本。相比之下，等值电阻法以整条线路为单位计算线损值，减少了计算所需的参数和计算量。这种方法的优势在于能够用更少的计算成本完成对配电网技术线损的计算，但是因为整条线路被视为一个等效电阻，所以无法准确地考虑到线路中各个设备的特性和电流分配情况，从而导致计算结果的精度相对较低。因此，在配电网技术线损计算中，需要寻找更合适的方法来克服均方根电流法和等值电阻法的局限性，以提高计算的准确性和效率。

2.3 回归分析法

回归分析是一种常见的数学方法，可以用于研究自变量与因变量之间的关系。在配电网技术线损计算中，我们可以使用回归分析来确定自变量（如电压、电流、有功功率、无功功率）与因变量（线损值）之间的联系，并通过建立回归方程来解决实际问题。具体步骤如下：（1）电力线路上的线损样本数据较多，涉及到电流、电压、功率等数值。（2）建立回归方程，利用好自变量和因变量之间的关系，确定好回归方程。在实际情况和问题分析中，在线性回归或非线性回归方程中自主选择。对于线性问题，可以使用线性回归方程进行求解；对于非线性问题，则需要使用非线性回归方程，如对数回归模型或多项式回归模型等。（3）利用建立的回归方程对线损值进行分析和计算。通过回归方程，可以根据给定的线损特征样本预测出线损值，从而对配电网的线损进行评估和优化。

回归分析的优势在于能够考虑到线损特征之间的相互作用，从而提高线损计算的准确性和效率。同时，回归分析方法也具有较低的计算复杂度，便于实际应用和计算。总之，回归分析是一种有效的方法，可以用于配电网技术线损计算，为优化配电网运行提供参考依据。

3 农村配电网技术线损评估模型

RBF神经网络，主要由输入层、隐藏层和输出层构成的三层前向神经网络。在应用RBF 过程中，隐含层的中心（ui）、激活函数的宽度（σi）和隐含层与输出层之间的权值（ω）这三个数值是非常重要的，这三个参数的准确性关系到非线性逼近能力。为了更好地应用RBF 神经网络，笔者主要通过PSO 算法优化这一内容，通过K-K-means++方法确定隐藏层数量、各个类别的中心，确定神经网络结构，为初始化PSO 提供借鉴。此外，将RBF 中激活函数宽度和初始聚类中心应用到PSO 当中，利用迭代计算法寻找最优解。通过不同适应情况，对激活函数宽度和隐含层节点不断更新优化，通过PSO 算法达到优化RBF设计的目的，获得隐藏层与输出层之间的权值、适应度值，对粒子速度及位置情况进行优化更新。对于迭代次数而言，可以通过PSO 算法判断是否达到最大值，如果已到最大值就终止算法，不然就重新返回至前一步骤。最后，将从算法中得出的最优参数应用在RBF当中，用于计算农村配电网技术线损值。

（1）确定隐含层数量和初始聚类中心

在本文中，对于线损特征情况，我们利用kmeans++算法进行聚类，根据算法结果来明确隐含层数量及隐含层节点的初始项链。在k-means++算法中，k数值是人为指定的，这一数值合理性关系到RBF 神经网络的性能发挥。为了确定合适的k 值和初始聚类中心，采用以下方法：首先，对数据使用不同的k 值进行聚类，并计算每个聚类结果的轮廓系数，轮廓系数综合了类内部的紧密程度和类间的分离程度，用于评估聚类的合理性；然后，从这些聚类结果中选择具有最高轮廓系数的结果作为合理的k 值和相应的聚类中心。

（2）编码与粒子群种群初始化

在RBF 神经网络中，为了更好了解其结构和编码，将之应用到PSO 算法当中，主要有如下7 个途径。① PSO 算法参数有最大更新速度、学习因子、种群规模和惯性权重等，进行初始化操作；② 对PSO 粒子空间维度、神经网络的连接权值，建立起映射关系；③ 对位置矩阵X 进行初始化设定。将群体定为N，利用激活函数宽度、初始聚类中心对第一个粒子位置进行初始化设定，而其他粒子位置则根据随机初始化的办法来确定；④ 对速度矩阵Y 进行初始化设定。我们也使用随机初始化的方法确定每个粒子的速度；⑤ 进行PSO 算法的迭代优化，直到达到最大迭代次数。在每次迭代中，根据当前的位置和速度，更新粒子的位置和速度；⑥ 在迭代的过程中，利用适应度函数评估每个粒子的适应度，并更新全局最优适应度和对应的位置。⑦ 最终，PSO 算法将找到最优的位置和相应的粒子，其中包含了最佳的RBF神经网络的结构。

式中，M=k（n+1），k为隐含层的节点数，n为输入特征向量的维数；表示群体中第i个粒子位置向量的第j维分量。

（3）计算隐含层与输出层的连接权值

在应用PSO 算法之后，迭代之后的状态中，我们能够从最优解中了解RBF 神经网络中的隐含层节点、确定激活函数数值。主要通过如下公示来确定隐含层及输出层之间的连接权值。

式中，wj是隐含层节点和输出层之间的连接权值，tj是隐含层节点的位置，ci是聚类中心，σi是激活函数的宽度。接下来，可以将RBF 神经网络应用于训练数据的线损值计算，从而得到在当前参数下的模型输出值。模型输出值可以用来计算适应度值，可以使用相关的评价指标（如均方误差）来衡量模型的拟合能力和准确性。通过迭代优化，PSO算法将在每次迭代中搜索到更好的参数配置，从而不断改善RBF神经网络的性能和拟合能力。

（4）计算每个粒子的适应度值

通过不断迭代PSO 算法，粒子将会搜索到更好的模型参数配置，以减小模型输出值与线损真实值之间的均方误差，从而找到更优的适应度值。这样，PSO 算法就可以学习到更合适的RBF 神经网络参数，提高模型的拟合能力和准确性。其定义如下。

式中，FitnessFunci维第i个粒字的适应度值；D（xi1，xi2，…，xim）为核函数参数（xi1，xi2，…，xim）情况下网络的凭据误差平方和，其计算公式如下。

式中，样本总数为p，输出层节点数为m，j样本中输出层的第i各节点实际输出值为，j样本中第i节点的预期输出值为。当输入特征向量为i时，的结果为1，相反则为0。

（5）更新粒子的速度和位置

对于PSO 算法的每个粒子i，可以使用以下方式更新粒子的速度和位置。

比较粒子i在本次迭代的适应度值与其历史最佳适应度值，不同的适应度值再进行数据更新。一般而言，当迭代适应度值较小时，对于粒子i而言，当前适应度值为最佳适应度值。通过对比粒子i的适应度值，将本次迭代与种群全局最佳值进行比较，在根据适应度值的大小情况，对内容进行更新。当本次迭代形成的数值更小的时候，将当前适应度值赋给全局最佳适应度值。

通过以上步骤，可以不断迭代更新粒子的速度和位置，以实现对适应度值的优化。

（6）判断算法终止条件

如果要判断算法是否达到最大迭代次数，则需要进行以下操作：

第一步，检查算法是否已经达到最大迭代次数。当迭代次数已达到最大值时，算法中止。不然就需要进行下一步操作。

第二步，重新计算粒子的适应度。根据当前的粒子位置和速度，重新计算粒子的适应度。

第三步，更新粒子群的位置和速度。及时参考最新粒子适应度和规则，更新粒子的速度和位置情况。

第四步，重复执行步骤2 和3，直到达到最大迭代次数或满足其他停止条件。因此，当迭代次数达到最高值，终止算法；不然，返回到第四步中，再次测算粒子的适应度。

（7）解码最优RBF神经网络参数

要确定RBF 神经网络的隐含层节点和激活函数，能够将群体优化当中的最优位置，设置为隐含层节点和激活函数宽度。当确定好相关函数之后，利用固定公式得出隐含层及输出层的连接值。

（8）运用最优RBF神经网络做线损计算

在RBF 神经网络当中，逐个将最优参数放置到其中，从而得出了最佳的RBF 神经网络。随后，可以使用这个最优的RBF 神经网络来计算技术线损，从而得到精确的结果。算法计算步骤如图1。

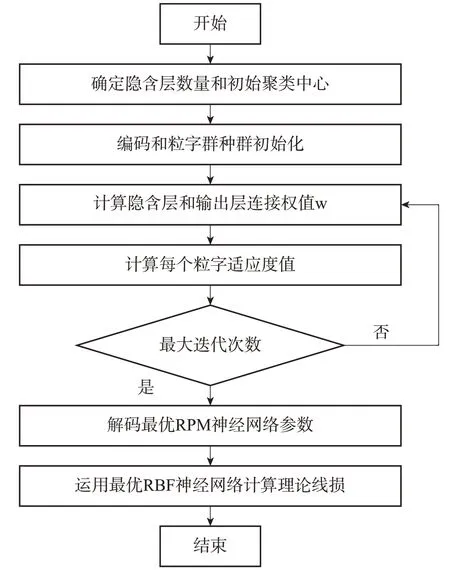
图1 PSO优化RBF神经网络计算技术线损流程图

4 结束语

本文针对农村配电网技术线损这一问题，建立了一种农村配电网技术线损特征分析与评估模型。该模型充分考虑了引起农村配电网技术线损变化的各种因素，如拓扑结构、设备类型、运行参数等，要联系好不同影响因子的影响程度及其关联性。在农村配电网中，其结构复杂、设备繁多、数据难获取等特征，使得技术线损的分析和评估面临一定的挑战。