基于Ansoft Maxwell的GIL三相交流稳态电动力仿真分析

任晓彪 陈晓鸣 陈浩杰 杨 涛 李松伟

（江苏安靠智能输电工程科技股份有限公司）

0 引言

电力系统中因为短路引起的故障较为严重，因此人们对短路故障下的母线电动力特性进行了广泛而深入的研究，也取得了不错的成效，使得GIL及母线的可靠性得到很大的提升。但对于正常运行中的电动力及其特性研究较少，目前运行中母线普遍存在振动和噪声较大的问题，可以将母线系统视为简单管道系统，而管道振动的实质是管道与之连接的设备，装置以及支架所构成的结构系统在上述随时间而变的复杂空间力系作用下的运动问题。显然，作用在管系上的力分析是关键。当力分析清楚即载荷确定之后，余下的问题就是求取在已知载荷作用下管系的振动响应［1］。因此，对正常运行中母线电动力的研究对于减小母线系统振动、降低系统运行噪音具有重要指导意义。

本文通过有限元法对三相电动力进行分析，首先建立三相有限元计算模型，通过施加不同的电流激励源，得到三相母线的电动力特性，并对三相电动力特性进行了分析，最后通过理论计算，将理论计算结果与仿真计算结果进行对比，二者基本一致。为分析正常运行中母线电动力特性提供了一种方法。

1 有限元仿真分析

1.1 仿真模型的建立

一般三相管型母线的排列顺序是三根管型母线导体在同一平面内相互平行［2］。为了减少计算工作量，提高计算精确度，本文采用二维平面模型，见图1。三相母线导体分别采用圆柱形结构，导体外径100mm，内径80mm，相间距260mm，导体为铝合金材质。

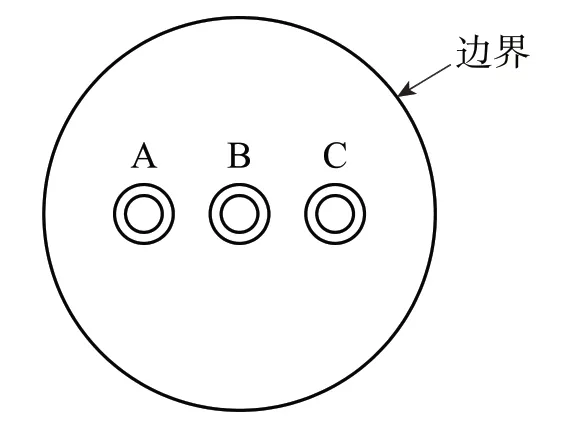
图1 三相水平母线计算模型

1.2 仿真计算前处理

本文使用Ansoft Maxwell 2D 磁场计算下的瞬态磁场求解器，用三角正弦函数模拟三相正常运行中的电流，将建立的模型导入Ansoft Maxwell，从左至右分别命名为A、B、C 相。三相电流相位分别差120°。三相电流函数分别如下式所示：

式中，iA、iB、iC分别为A、B、C 三相在t时刻的瞬时电流，Im为稳态交流电流的幅值。

实际运行中，三相线路中通过正弦交流电流，由于电磁感应的作用，导线处在负荷电流和涡流产生的交变电磁场中，因此三相导线之间互相受到磁场力的作用［3］。将公式（1）~（3）作为电流激励源分别施加在A、B、C三相母线导体上。

1.3 网格划分及求解器设置

Maxwell 软件网格剖分采用了金字塔型剖分设置，可以不需要用户过多的参与剖分，直接利用内置的自适应剖分也可以得到正确的计算结果同时采用了较少的计算时间［4］。在本文中，为了提高计算精度，除了采用自适应网格剖分外，还采用On Selec‐tion 剖分设置中的Length Based refinement 设置，Length Based refinement 是基于单元边长的剖分设置，这里设置导体网格单元长度为1mm，气体域网格单元边长为2mm，图2 为最终的离散化模型，图3 为加密后的三相导体附近网格模型，可以看出，越靠近中心导体处，网格剖分越细密。

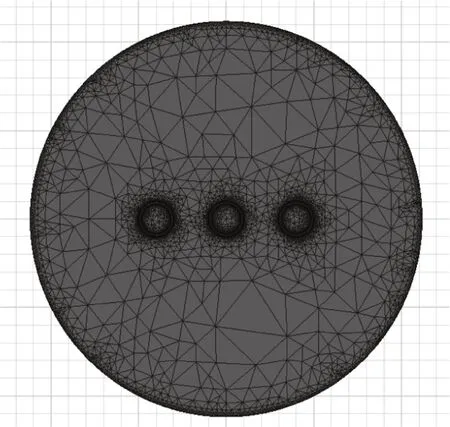
图2 整体网格剖分模型

图3 导体附近网格剖分模型

对2D 瞬态磁场求解器进行设置，设置求解时间为0.2ms，计算时间步长设置为0.0001s，同时对计算时的场结果储存时间及步长进行设置，这里与求解设置一致，并将设置好的存储时刻保存在状态栏中。

1.4 求解分析

对上述模型进行瞬态磁场求解，并读取电流3000A 时三相电动力结果，求解出的三相电动力如图4-6所示。

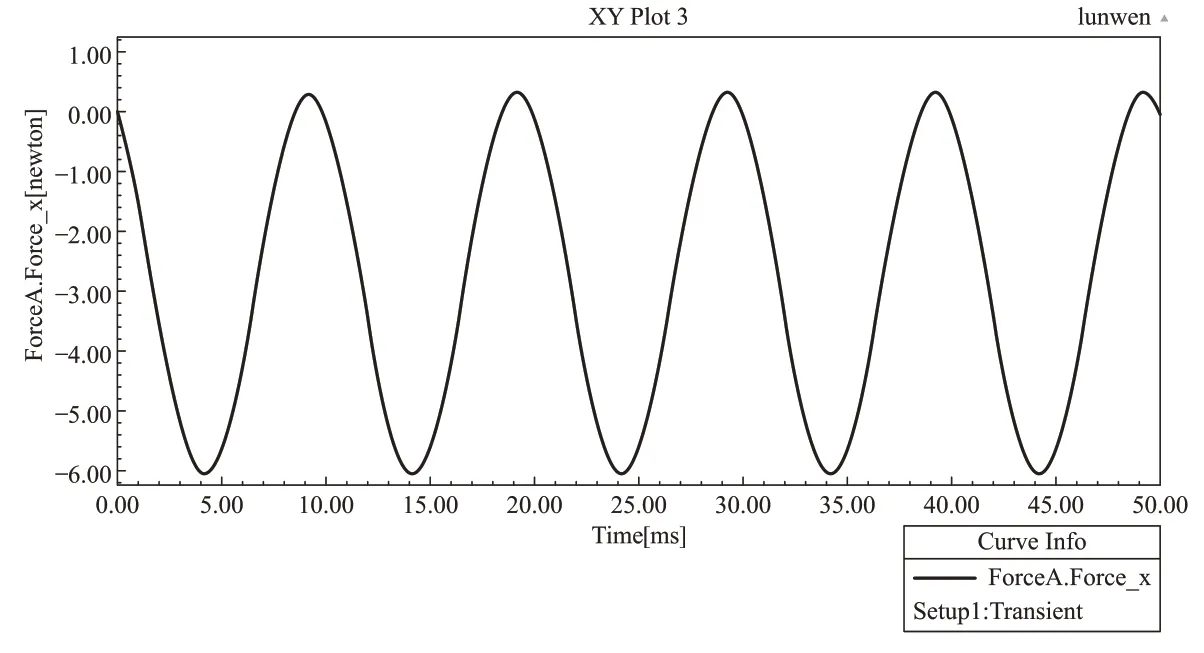
图4 A相电动力曲线

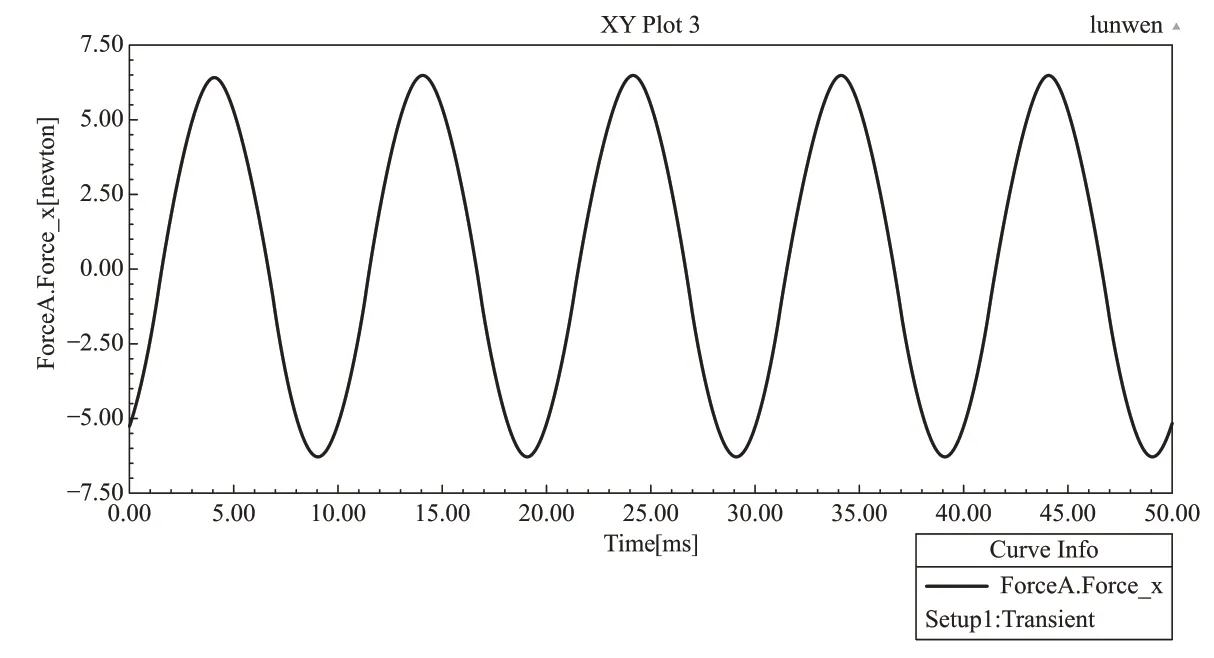
图5 B相电动力曲线

由图6 可知，三相导体所受电动力呈周期性波动，且频率一致，均为工频的两倍，最大电动力值发生在B 相，发生时刻在4.2ms，最大电动力为6.39N/m，此时，A 相电动力为6.04N/m，C 相电动力为0.39N/m，整个周期中，A 相与C 相电动力幅值基本相等，但到达幅值的时间不同。图7 为B 相电动力最大时刻即4.2ms 时的电磁场分布云图，从图上可以看处，此时B 相导体附近磁场强度最大，A 相次之，C 相电磁场强度最小，该结果与电动力结果基本一致。

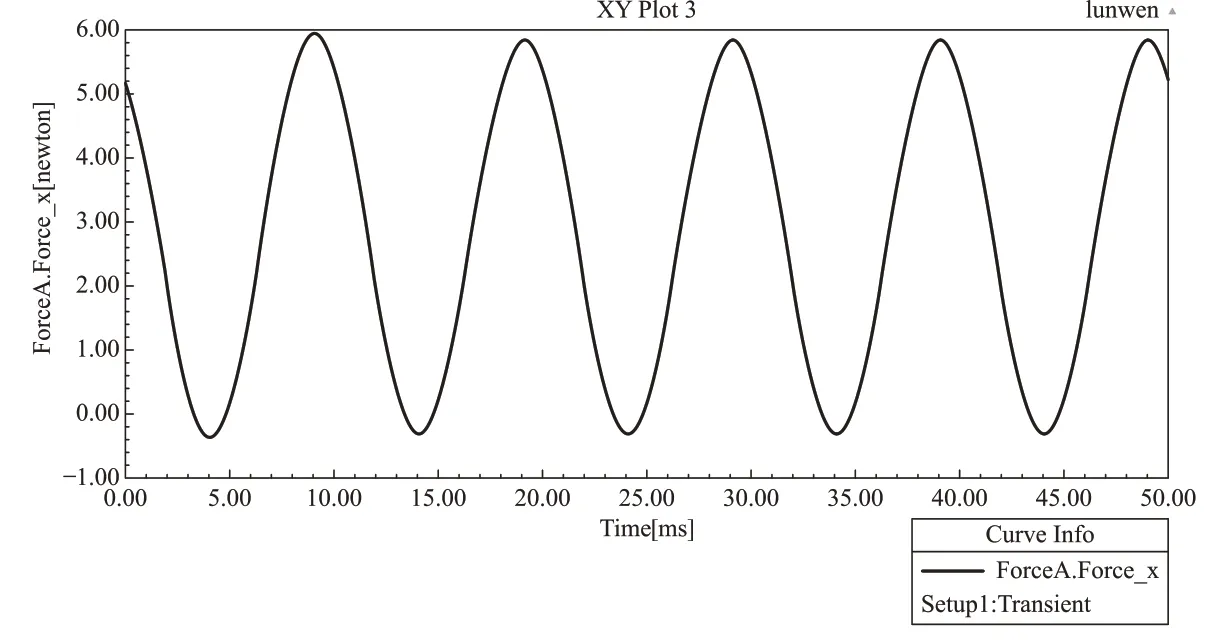
图6 C相电动力曲线

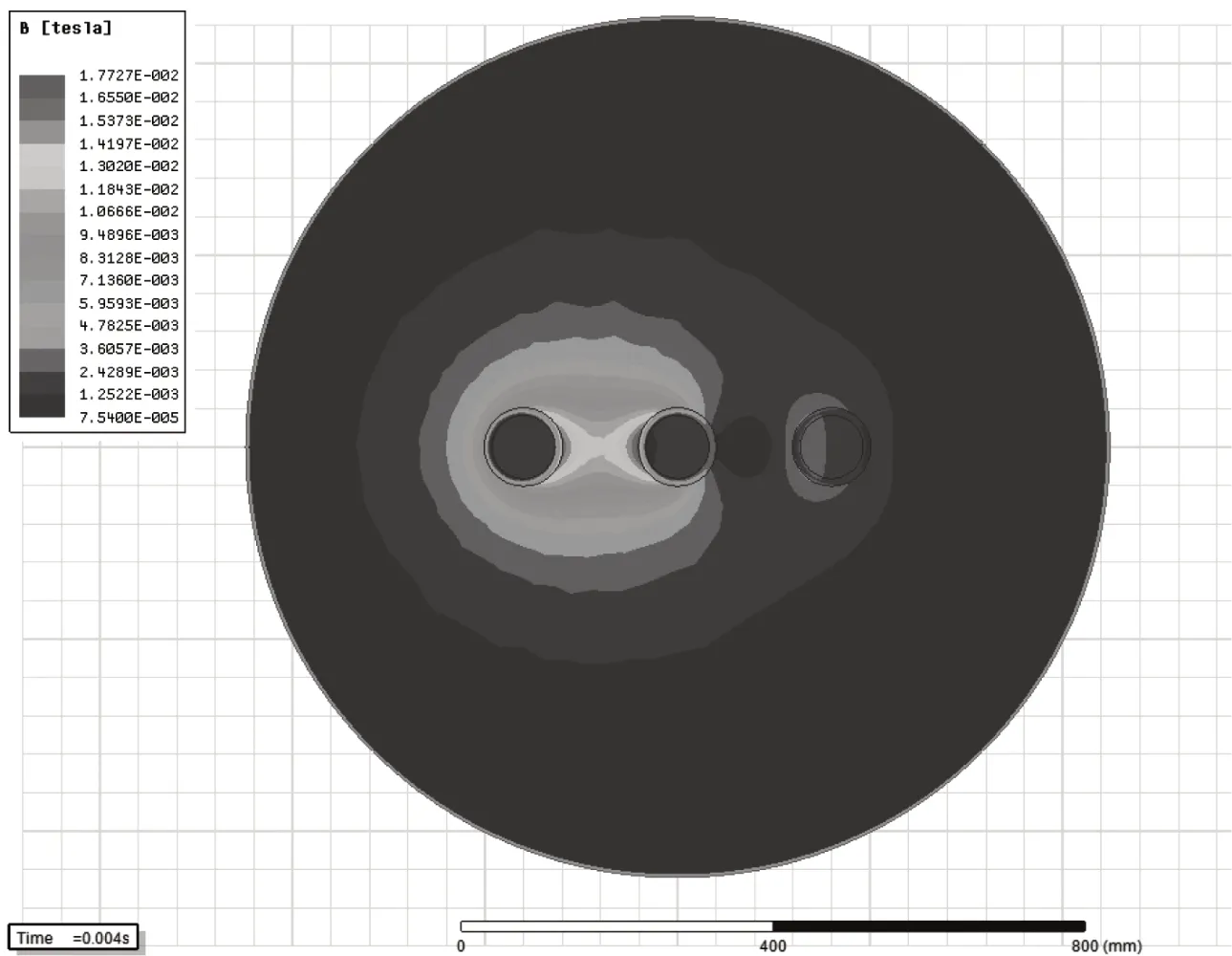
图7 电动力最大时磁场强度分布云图

2 三相电动力的公式法计算

载流导体在磁场中受到磁场对电流的作用力称为电动力，该力的大小和方向与导体所通过电流的大小，方向有关，电动力计算常用的方法有两种，比奥-沙瓦定律和能量平衡法，比奥-沙瓦定律是最常用的方法，本文采用比奥-沙瓦定律进行三相电动力的理论计算。

根据比奥-沙瓦定律，同一平面上两细长导体电动力的计算公式可以表示为：

式中，I1、I2分别为两平面导体中通过的电流值（A）。Kh称为回路系数，是一个无量纲系数，其与所研究回路系统两导体的相对位置及形状有关。对两个无限长平行导体

式中，a为两导体的相间距离（m）；l为导体长度（m）；将式（5）代入式（4）中，得到两平行导体电动力的计算公式：

式中，电动力F 的方向与流过两导体中的电流方向相关，当两导体中电流方向相同时，表现为排斥力，反之表现为吸引力。

将式（1）、（2）、（3）分别带入式（6）中，分别求取三相导体所受电动力。

2.1 A相导体所受电动力

A 相导体所受电动力可以看做是B 相电流及C 相电流单独作用的迭加。可以分别求取B相对A相的电动力FBA、C相对A相的电动力FCA。

因此，当ωt=n*π+75 （n=0，1，2，3，…）

求得：(FA)max=5.64N/m

当ωt=n*π+165 （n=0，1，2，3，…）求得：(FA)min=0.40N/m

将图6 中A 相的电动力仿真结果最大值及最小值与计算结果相比较，A 相电动力呈周期性分布，且电动力最大时刻的值为，最小时刻的值为，与公式计算结果一致。

2.2 B相导体所受电动力

B 相导体所受电动力可以看做是A 相电流及C 相电流单独作用的迭加。可以分别求取A相对B相的电动力FAB、C相对B相的电动力FCB。

因此，当ωt=n*π+75 （n=0，1，2，3，…）

求得：(FB)max=5.99N/m

当ωt=n*π+165 （n=0，1，2，3，…）

求得：(FB)min=-5.99N/m

将图7 中B 相电动力仿真结果最大值及最小值与计算结果相比较，B 相电动力呈周期性分布，且电动力最大时刻的值为，最小时刻的值为，与公式计算结果一致。

C 相导体与A 相导体相对于中心线完全对称，因此C相所受到的电动力最大值与最小值和A相完全相同，只是出现最大值与最小值的时间不同。图8为A、B、C 三相电动力分布图，从图中也可以明显看出，AC 相电动力最大值与最小值大小相等，但是到达极值的时间不同，而B 相电动力相对于X 轴对称分布，最大值与最小值大小相等，方向相反。

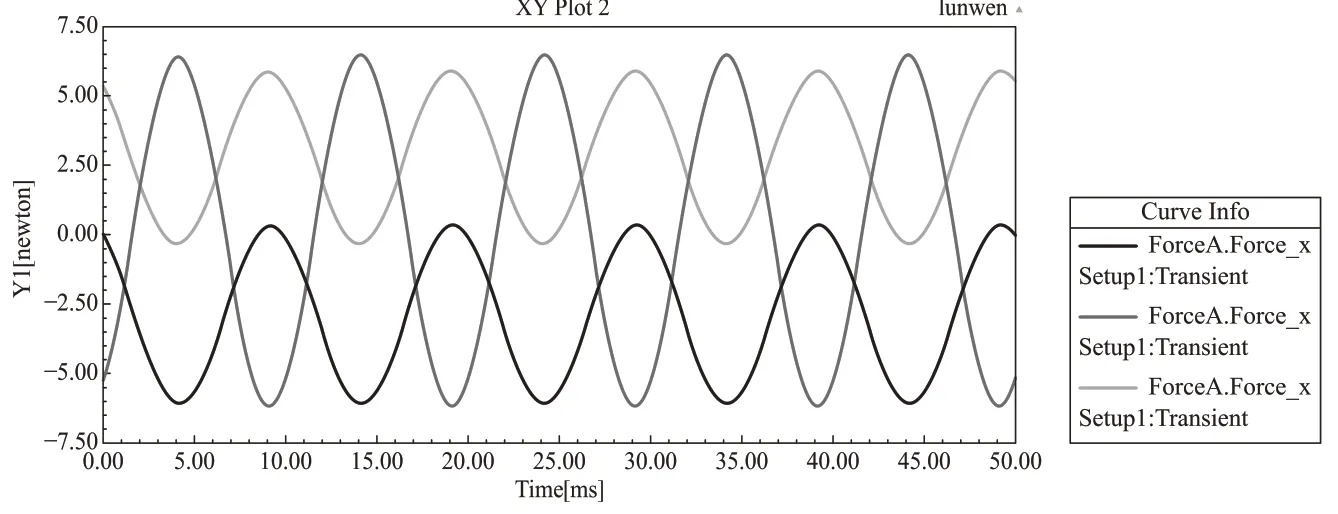
图8 三相电动力分布图

3 仿真计算与公式法计算结果比较

表1 中对ωt=n*π+75 （n=0，1，2，3，…），ωt=n*π+165 （n=0，1，2，3，…）两个时刻的电动力仿真结果与公式法计算结果进行了对比，从表中可以发现，仿真结果与理论结果误差较小，这些误差主要是理论计算结果不考虑导体形状以及涡流效应对电动力的影响。

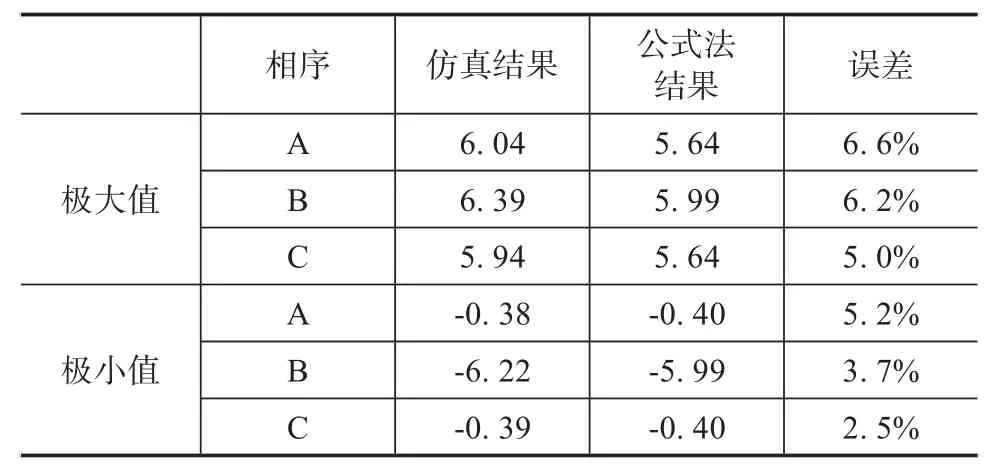
表1 仿真计算与公式法计算结果比较

4 结束语

通过对三相水平母线电动力的仿真计算及公式法计算，得出以下结论：1）三相水平布置母线导体，在正常运行下所受电动力最大值发生在B 相，B 相最大值约为A、C 相的1.07 倍。2）仿真计算电动力值略高于公式法计算电动力值，这主要是因为公式法计算没有考虑到导体形状及涡流效应对电动力的影响。正常运行下三相母线电动力值均较小，最大不超过6.39N/m，因此在设计时重点考考虑短路电动力即可。