动态膜厚的超声实时测量方法及测量盲区影响因素

孙 炜, 梁 鹏,2*, 郭 峰, 孔令胜, 姜芙林, 白清华, 刘晓玲

(1. 青岛理工大学 机械与汽车工程学院, 山东 青岛 266520;2. 青岛理工大学 工业流体节能与污染控制教育部重点实验室, 山东 青岛 266520)

在齿轮、滑动轴承和滚动轴承等相对旋转工件的运动过程中，需要在运动表面注入适量润滑剂、使两摩擦面分离，从而减小摩擦系数、降低振动噪声. 摩擦副表面的润滑剂厚度是润滑质量的重要表征之一，润滑膜太薄会导致摩擦副表面发生干摩擦引起过量磨损，而润滑膜过厚会导致漏油现象[1]的发生致使设备承载能力下降. 因此，为保障机械设备高效安全运行，需要对摩擦副表面之间的润滑剂厚度进行实时监测.

目前常用的润滑膜厚度测量方法分为光学法、电学法、电磁法和超声波法. 光学法要求被测对象具有良好的透光性[2-5]，电学法测量得到的是膜厚平均值[6-9]，电磁法[10-13]适合用于导电材料[14]. 上述3种测量方法在应用领域发挥着各自的优势，但上述方法对材料的特殊物理要求限制了其在工程实际领域膜厚测量的进一步应用. 超声波法对摩擦副材质没有特殊要求，可通过分析声波在摩擦副及润滑剂内的传播规律来测量膜厚，具有良好的穿透性、非侵入性和无材质要求等特点，目前越来越引起国内外学者的重视.

基于超声波技术的膜厚测量方法主要分为时域和频域2种方法. 在时域法方面，Dwyer等[15]提出利用信号处理方法获得反射波的时间间隔来计算润滑膜厚度；但当反射波相互重叠时无法获取时间间隔，因此Praher等[16]提出在时域中利用不同幅值和相位的标准信号来重构叠加信号，再将叠加信号与实际测量信号匹配，从而得到超声波在润滑剂中的传播时间；Dou等[17]对该算法进行了插值优化，使其具有更大的有效测量范围. 在频域法方面，共振模型[18-21]和弹簧模型[22-24]都是将反射信号和参考信号进行快速傅里叶变换得到频域信息，使用相应模型来求解润滑膜厚度.Pialucha等[18-19]提出当润滑膜厚度为超声波半波长的整数倍时，入射波和反射波会发生共振现象，追踪得到共振频率点从而求解润滑膜厚度. Drinkwater等[24]提出将润滑膜看做等效弹簧，通过数学方法推导弹簧模型公式，利用反射系数直接求得润滑膜厚度. 然而，目前在利用超声波方法测量膜厚时，弹簧模型和共振模型的膜厚测量范围之间存在测量盲区[25]，传统方法需要更换不同频响探头来尝试覆盖测量盲区，即当前研究还无法实现单个探头对宽范围全域膜厚的测量.此外，目前缺乏关于动态变化膜厚的实时在线超声测量研究. 为解决上述问题，本文中提出1种可覆盖测量盲区且同时利用频域信息和相位信息的复合模型，并利用自行搭建的膜厚超声在线测量系统研究了摩擦副配副方式和润滑剂种类对测量盲区的影响. 最后，对超声测量试验进行了仿真模型构建，研究了超声波在不同摩擦副和不同润滑剂内部的声压传播规律. 本文工作为摩擦副在实际工况下的动态膜厚状态监测提供了技术借鉴.

1 基于超声波技术的润滑膜厚度测量模型

图1 所示为超声波在3层介质(上摩擦副-润滑剂-下摩擦副)模型中的传播过程，当入射波I到达分界面1时，由于分界面两侧介质的声阻抗不同，超声波将产生反射波b1与透射波；当透射波继续传播到分界面2时再次发生反射现象与透射现象(产生透射波a1)，而产生的反射波将返回到分界面1继续发生反射现象和透射现象.

Fig. 1 Propagation model of ultrasonic wave in three-layer medium图1 超声波在3层介质中的传播模型

根据位移与应力连续方程，可得分界面1处声波反射系数R的表达式[20]：

式中，h为润滑剂厚度，z2为润滑剂声阻抗，z1、z3分别为润滑剂两侧摩擦副的声阻抗，c2为润滑剂中的声速，ω为超声波的角频率，i为虚数单位.

根据复变函数公式e(ix)=(cosx+isinx)，将式(1)变换为

对式(2)进一步简化可得：

1.1 共振模型

当润滑剂厚度h为声波半波长的整数倍时，入射波与反射波发生共振[18-19]，此时反射系数的频域幅值出现极小值(即共振点)，将对应的共振频率带入共振模型(4)可求解润滑膜厚度[18-21]：

式中，fres为极小值点对应的共振频率，n为共振阶数.

1.2 弹簧模型

当润滑剂厚度h远小于声波半波长时，共振模型由于高频衰减[26]的原因不再适用. 由式(2)推导得到反射系数幅值|R|的表达式：

由于z2与z3相比很小，上式与油膜刚度有关，可得到弹簧模型公式：

式中，ρ2为润滑剂密度，f为超声波脉冲频率.

1.3 复合模型

当利用上述模型测量润滑膜厚度时，弹簧模型测量范围与共振模型测量范围之间存在较大空白区域(即测量盲区)，传统方法需尝试不同中心频率的探头才可实现盲区膜厚测量，存在成本高、耗时长的问题.为实现单个探头对宽范围膜厚的全域测量，需要提出1种新模型来覆盖上述测量盲区. 弹簧模型和共振模型只利用了反射系数的幅值信息，如果能既利用幅值信息又同时利用相位信息将会扩大膜厚的测量范围.由式(2)可求得反射系数相移φR的表达式：

联立式(5)和(7)可得：sin-2φR=tan-2φR+1

将式子带入上式可得：

因此膜厚h(|R|,φR)的计算公式为

由于z2和z3相比很小，上式可化简为

润滑剂声阻抗z2=ρ2c2，上式进一步化简可得：

当上下摩擦副材质相同时(即z1=z3=z)，基于复合模型的膜厚计算公式为

由式(12)和(13)可知，在复合模型中可同时利用反射系数幅值|R|和相移φR计算润滑剂厚度.

2 膜厚动态调整系统

本文中搭建了1套可实现润滑膜厚度动态调整的系统[27]，包含膜厚调整单元、信号采集单元及数据处理单元(图2). 图2(a~b)所示分别为膜厚调整系统的原理图和实物图，膜厚调整单元主要由位移升降台、2个正交分布的电动角位移台、上摩擦副、下摩擦副、压电陶瓷及PZT控制器组成. 信号采集单元由超声波探头和脉冲发射/接收仪(UPR)组成，超声波探头的型号为V111-RM (中心频率为10 MHz). 数据处理单元由示波器和PC机组成，示波器将UPR传输的信号进一步传递到PC机中，利用LabVIEW软件搭建的膜厚测量系统对反射波进行快速傅里叶变换，基于3个模型(共振模型，弹簧模型及复合模型)计算润滑膜厚度. 膜厚的动态调整原理如图2(b)所示，将下摩擦副固定在压电陶瓷上，通过PZT控制器与PC机的连接，可控制压电陶瓷输出不同规律(如正弦波)的位移，带动下摩擦副往复运动，从而动态调整上下两摩擦副之间的膜厚.依靠压电陶瓷的控制，膜厚调整分辨率可达2 nm，电动角位移台的倾角分辨率可达0.005°，膜厚调节的频响范围0~60 Hz.

Fig. 2 Diagram of experimental equipment图2 试验设备示意图

在图1中，润滑剂的类型以及摩擦副的材质、配副方式均对超声波的传播过程有重要影响. 如图3所示，本文中采用水、1#润滑油和2#润滑油共3种润滑剂，研究润滑剂类型对膜厚测量的影响规律. 1#润滑油为PAO10，黏度为110.3 mPa·s；2#润滑油为PAO20，黏度为232.4 mPa·s. 试验中所使用的摩擦副为亚克力(PMMA)、304不锈钢、玻璃和铝，配副方式分别为铝/PMMA、铝/玻璃和铝/304不锈钢. 润滑剂及摩擦副的物理参数列于表1中.

表1 摩擦副和润滑剂的物理参数Table 1 Physical parameters of lubricants and friction pairs

Fig. 3 Different lubricants and friction pairs图3 不同润滑剂及摩擦副

3 基于超声波技术的膜厚在线测量及测量盲区研究

3.1 润滑膜厚度的动态实时测量

3.1.1 实时测量系统

为实现反射声波信号在线处理及膜厚实时测量，本文中基于LabVIEW软件搭建了图4所示的膜厚在线测量系统. 测量系统包含共振模型、复合模型和弹簧模型3个模块. 图4(a~c)所示分别为3个模块的前面板，均包括3个区域：参数输入区、图像显示区和数据显示区. 以弹簧模型模块的前面板为例，参数输入区包括声波速度、润滑剂密度、探头型号、摩擦副材料和参考信号，图像显示区则包括反射信号的频域幅值图、参考信号的频域幅值图、反射系数幅值图及膜厚图.

Fig. 4 Real-time measurement system of lubricant thickness based on ultrasonic technology图4 基于超声波技术的膜厚实时测量系统

3.1.2 复合模型的测量步骤

利用图2(a)试验台并结合3种模型可对膜厚进行动态测量. 由于3种模型的测量步骤差别不大，因此仅以提出的复合模型为例介绍膜厚测量步骤(图5)：

Fig. 5 The measurement steps of the composite model图5 复合模型的测量流程

a. 采集参考信号：在无润滑剂情况下，使用超声波探头采集摩擦副-空气界面的时域信号(即参考信号)，并利用快速傅里叶变换(FFT)得到频域下的幅值信号A1(f)和相位信号φ1(f).

b. 采集反射信号：按照创建的“正交三点法”[28]利用角位移台将两摩擦副调平后，在摩擦副之间缓慢注入足量的润滑剂，使用探头采集摩擦副-润滑剂界面的时域信号(即反射信号)，并利用FFT得到频域下的幅值信号A2(f)和相位信号φ2(f).

c. 计算|R|sinφR值：将步骤(1)和(2)中的幅值信号与相位信号带入公式|R(f)|=A2(f)/A1(f)和φR(f)=φ2(f)-φ1(f)，可求得摩擦副-润滑剂界面的参数值|R|sinφR.

d. 求解膜厚：将|R|sinφR参数值带入复合模型公式(12)或(13)可得两摩擦副之间的润滑膜厚度.

3.1.3 膜厚变化周期及类型对动态测量的影响

为研究膜厚动态变化特性对测量精度的影响，对不同变化周期及变化类型时的膜厚进行了测量分析.试验中的上下摩擦副材质均采用不锈钢，润滑剂选择纯水.

图6 (a)给出了不同膜厚时的反射信号时域曲线.与图6中参考信号相比，随着润滑膜厚度减小，反射信号曲线呈现幅值减小、相位滞后的趋势. 将时域信号进行快速傅里叶变换可得反射系数的频域幅值曲线[图6(b)]. 图6(b)中每条曲线均存在黑色实心标记的极小值点，对应的是公式(4)中用于计算膜厚的共振频率fres.但需要注意，并非所有极小值点都是共振点，在有效带宽(-12 dB)之外左侧虚线圆圈里的极值点则是周围环境噪声造成的伪共振点. 膜厚计算值随图6中共振频率的增大而减小，这符合共振模型(4)所呈现的反比关系.

Fig. 6 Time domain curve and frequency domain curve with different film thickness图6 不同膜厚时的信号时域曲线和频域曲线

将图2压电陶瓷的输入电压设置为三角波规律，周期分别为1、2和3 s. 利用图4自行编制的在线测量系统进行膜厚的动态跟踪测量. 图7所示为不同周期时三角波膜厚的动态跟踪结果. 从整体变化趋势来看，膜厚的动态测量结果与三角波变化规律完全一致. 当周期分别为1、2和3 s时，对应的最大相对误差分别为2.01%、1.76%和1.35%，平均相对误差分别为0.89%、0.80%和0.55%，这表明在线测量系统对动态膜厚的跟踪误差较小，且最大测量误差和平均相对误差均与波形周期呈反比.

Fig. 7 Influence of period on dynamic measurement of triangle wave film thickness图7 周期对三角波膜厚动态测量的影响

为进一步研究变化周期及类型对动态膜厚测量的影响，将压电陶瓷的输入电压分别设置为正弦波、三角波、锯齿波和矩形波4种规律，如图8(a)所示. 且每种波的周期分别设置为1、2和3 s. 图8(b)所示为不同波形及不同周期下的膜厚测量误差. 可以看出：(1)不论在何种周期下，矩形波规律的膜厚测量精度最高，三角波和正弦波的膜厚测量精度略低，而锯齿波的膜厚测量精度最低. 例如，周期2 s时，正弦波、三角波、锯齿波和矩形波时的膜厚最大测量误差分别为1.69%、1.76%、1.95%和0.79%，膜厚的平均测量误差分别为0.76%、0.80%、0.98%和0.57%. (2)膜厚的平均测量误差随变化周期的增大而减小. 例如，在锯齿波情况下，周期为1、2和3 s的平均测量误差分别为1.24%、0.98%和0.69%. (3)在3种变化周期的矩形波时，平均相对误差分别为0.60%、0.57%和0.56%，表明超声波技术跟踪矩形波膜厚的精度最高且最稳定. (4) 4种变化规律及3种变化周期时的膜厚最大测量误差均低于3%，表明了本文中搭建的测量系统在动态膜厚在线测量方面的可行性及精确性.

Fig. 8 The influence of film thickness variation type and period on measurement accuracy图8 膜厚变化类型及周期对测量精度的影响

图8 (b)中测量误差的重要来源之一是示波器的分辨率. 受限于示波器固有的分辨率(Δf1=0.4 MHz，即反射系数频域幅值曲线中相邻2个点之间的间距为0.4 MHz)，实际测量得到的共振频率与理想共振频率fres存在一定差距，导致测量膜厚与理论膜厚具有误差.

图9 所示为膜厚测量误差分析图，图9中黑色平滑曲线表示理论膜厚随频率的变化. 假设A点为第1次测量点，共振频率为7.2 MHz，膜厚为102.8 μm. 若降低膜厚2.8 μm，第2次测量的理论膜厚应为100 μm，对应的理论共振频率应为7.4 MHz，即图中C点. 但受限于示波器固有的分辨率(Δf1=0.4 MHz)，无法捕捉到理论共振频率，实际得到的共振频率为7.6 MHz，且对应的膜厚为97.4 μm，即图中B点. 实际测量点B与理论测量点C的膜厚差Δh=100-97.4=2.6 μm，共振频率差Δf=7.6-7.4=0.2 MHz. 综上所述，示波器固有的分辨率是膜厚测量误差的主要因素之一.

Fig. 9 Analysis of measurement error of film thickness图9 膜厚测量误差的分析

3.2 配副类型对测量盲区的影响

摩擦副材质不同，与润滑剂的分界面处反射系数也不同，因此不同材质摩擦副时膜厚测量范围及测量盲区也不同. 本部分研究不同类型的配副对测量盲区的影响，选择的3种配副方式分别为铝/PMMA，铝/玻璃和铝/304不锈钢，润滑剂选择纯水.

3种配副时的膜厚测量结果如图10所示. 从图10(a~c)可以看出，弹簧模型(天蓝色区域)和共振模型(桃红色区域)的膜厚测量范围之间存在明显的测量盲区(即中间白色区域)，3种配副时盲区范围分别为17~40、18~39和20~37 μm，为解决盲区测量问题传统方法需要尝试不同型号的探头. 而本文中提出的新型复合模型测量范围分别为15~50、13~55和8~65 μm，完全可以覆盖上述3个测量盲区，意味着利用弹簧模型、共振模型及提出的复合模型，可实现单个探头对宽范围膜厚的全域连续测量，这是传统方法不能实现的.

Fig. 10 Measurement results of film thickness with different matching pairs图10 不同配副时的膜厚测量结果

为更加直观地分析配副类型对膜厚测量范围的影响，将图10(a~c)中的测量结果汇总到图10(d). 图中红色曲线表示不同配副利用3种模型测量时的最大相对误差. 随着下摩擦副声阻抗的增大，3种模型的测量范围逐渐增大，而测量盲区逐渐减小. 例如，304不锈钢(45.897×106N·s/m3)的声阻抗大于玻璃(14.793×106N·s/m3)，且远大于PMMA (3.27×106N·s/m3)，结果表明铝/304不锈钢时的测量盲区(20~37 μm)最小，而铝/PMMA时的测量盲区(17~40 μm)最大. 这是因为图1中润滑剂-下摩擦副分界面的反射系数随下摩擦副阻抗的增大而增大，导致反射信号B2变强、膜厚测量范围变大. 以上结果表明不同配副的组合方式会显著影响3个模型的测量范围及测量盲区.

图11 所示为配副为铝/玻璃时的膜厚测量结果.图11(a)所示为不同膜厚时的反射系数幅值曲线. 当频率相同时，反射系数幅值随膜厚增大而增大. 在同一膜厚曲线情况下，反射系数幅值随频率增大而先增大后逐渐稳定. 在有效带宽(-6 dB)范围内，润滑膜厚度较小时(如6、7和8 μm)，不同膜厚的反射系数幅值曲线之间区分明显. 但随着膜厚增大，反射系数幅值曲线的区分度变小(图中黑色虚线框内的部分)，特别是当膜厚为16和18 μm时，两曲线之间互相纠缠难以区分[29]，而且部分反射系数幅值大于极限值0.95[30]，这些数据并不符合弹簧模型的使用条件，即弹簧模型测量范围已达到极限.

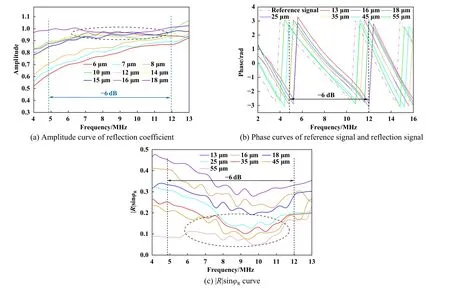
Fig. 11 Measurement results when the matching pair is Aluminum/Glass图11 配副为铝/玻璃时的测量结果

将时域信号进行快速傅里叶变换，可得润滑膜的相位信息，如图11(b)所示. 相位曲线随频率的变化呈锯齿状规律. 当膜厚增大时，反射信号相位曲线具有趋近参考信号相位曲线的规律，这可能和参考信号近似为无穷大膜厚时的反射信号有关. 同一频率下，随着润滑膜厚度的增大，反射信号与参考信号的相移逐渐减小.

图11 (c)给出了|R|sinφR的变化规律. 在相同频率情况下，|R|sinφR随膜厚增大而减小；在相同膜厚时，|R|sinφR曲线随频率的增大呈现先减小后上升的趋势.当膜厚超过12 μm时，图11(a)的反射系数幅值曲线就开始相互纠缠、难以分辨，但在图11(c)中膜厚大于12 μm的|R|sinφR曲线具有清晰的区分度，例如膜厚为13和16 μm时两曲线具有明显区别. 因此，复合模型可以覆盖弹簧模型在较大膜厚时无法测量的盲区. 当然，膜厚增大到一定程度(如45和55 μm)，|R|sinφR曲线的区分度也开始变小.

3.3 润滑剂类型对测量盲区的影响

不同润滑剂的黏度、弹性模量以及密度等物理参数也不同，导致超声波在不同润滑剂里的传播速度、声阻抗有显著区别，这会影响膜厚的测量范围及测量精度. 因此本部分研究不同类型的润滑剂对超声探头测量盲区的影响. 试验中的上下摩擦副材质均为304不锈钢，润滑剂分别为水、1#润滑油(PAO10)和2#润滑油(PAO20).

采用TOF法[15]来测量润滑剂内的声速，利用示波器获得图1中反射波b2和b3被接收的时间差Δt，并结合传播距离可求出声波在润滑剂内的速度. 图12给出了3种润滑剂时的反射信号时域图，选取b2和b3信号的最大振幅(此处声波能量最大)作为比较点，可得3种润滑剂时的时间差分别为Δt1=1.363 μs，Δt2=1.442 μs和Δt3=2.028 μs，利用TOF法的公式c=2h/Δt(h=1000 μm)可计算声波在3种润滑剂内部的传播速度. 与1#润滑油和水相比，2#润滑油时的反射信号出现整体右移现象，且反射波的时间差Δt明显增大，这均是由于声波在2#润滑油中传播速度较小所致.

Fig. 12 Time domain signal of reflected wave with different lubricants图12 不同润滑剂时的反射声波时域信号

图13 给出了不同润滑剂时的膜厚测量结果，每种模型(弹簧模型，复合模型，共振模型)在不同润滑剂时的测量范围是不同的，且弹簧模型与共振模型之间的测量盲区也与润滑剂类型紧密相关. 为更加直观地分析润滑剂类型对膜厚测量盲区的影响，将图13中的测量结果汇总到图14(a). 可以看出：(1)随着润滑剂声阻抗的减小，3种模型的膜厚测量范围均呈现减小趋势.例如，润滑剂为水(声阻抗1.477×106s/m3)时复合模型的测量范围是7~43 μm，而润滑剂为1#润滑油(声阻抗1.168×106s/m3)时复合模型测量范围缩小为5~25 μm；(2)测量盲区(图中斜剖面区域)随润滑剂声阻抗的增大而出现略微减小趋势. 由于复合模型与共振模型测量范围随润滑剂声阻抗减小而明显减小，致使复合模型与共振模型之间出现“测量真空区”(图中紫色箭头表示的范围)，即3种模型均无法测量该膜厚范围. 例如，1#润滑油时的“测量真空区”范围25~39 μm，而2#润滑油的“测量真空区”范围17~39 μm. 这是因为当图1中润滑剂声阻抗减小时，超声波在分界面1的透射系数降低，导致后续携带膜厚信息的反射信号b2减弱，故膜厚的可测范围减小、出现“测量真空区”；(3)共振模型的测量下限没有变化，这是由于共振频率已经超出了有效带宽范围，超声波随频率增加而严重衰减，因此无法改变测量下限[26]. 图14(b)给出了不同润滑剂时膜厚测量结果的误差，所有试验结果的最大相对误差均不超过5.50%，同一种润滑剂时3个模型的最大误差(或最小误差)几乎一致.

Fig. 13 Measurement results of film thickness with different lubricants图13 不同润滑剂时膜厚的测量结果

Fig. 14 Measurement range and relative error of film thickness with different lubricants图14 不同润滑剂时膜厚测量范围和相对误差

4 超声波在介质中传播过程的仿真分析

为进一步解释第3部分的试验结果，本文中利用COMSOL Multiphysics多物理场仿真软件对试验过程进行了建模与研究.

4.1 不同配副类型时的声波传递仿真计算流程

超声波在介质传播模型的计算流程如图15所示，通过CAD建立3层介质模型，并导入COMSOL进行压力声学瞬态仿真，首先进行物理场的选择和初始参数的设定，对固/水域和边界条件分别进行设置，在划分网格后进行迭代计算，最终可得超声波在3层介质中声压随时间的变化规律. 确定仿真过程中的重要参数，时间步设定为1/(30*f0)，放大高频设置为0.5，声压的迭代收敛精度1×10-5.

Fig. 15 Calculating process of model图15 模型计算流程图

4.2 模型可靠性验证

为验证本文中COMSOL分析模型的可靠性，对参考文献[31]中的超声传播模型进行了仿真对比，声波传播距离及介质均按照参考文献设置. 仿真得到介质1—介质2分界面处的回波信号声压，与参考文献的对比结果列于表2中. 可以看出，模型计算声压与参考文献声压有很好的一致性，相对误差范围为1.03%~2.95%，验证了本文中COMSOL计算模型的有效性和准确性.

表2 本文计算声压与参考文献声压的对比Table 2 Comparison of calculated acoustic pressure and reference acoustic pressure

4.3 不同配副类型时的声波传递仿真过程

4.3.1 建立模型

为解释3.2部分的测量结果，分析不同配副类型时的声压传递规律，本部分利用COMSOL Multiphysics软件将试验模型等效为二维轴对称模型，如图16(a)所示，模型采用瞬态压力声学分析模块. 将上阻抗边界设置为铝，下阻抗边界分别设置为PMMA、玻璃和不锈钢. 模型通过设置圆柱形的完美匹配层来模拟无限远处的声场边界. 模型的网格划分结果如图16(b)所示，包括压电陶瓷网格、水域网格以及完美匹配层网格.

Fig. 16 Simulation model of acoustic pressure distribution with different pair types图16 不同配副类型时声压分布仿真模型

网格数量和自由度数对仿真结果有较大影响，因此本文中探讨了网格数量及自由度对网格质量、计算速度和精度的影响(表3). 以透射信号接受边界处的声压作为目标声压，使用5种不同数量和自由度的网格进行结果比较. 由表3可知，随着自由度和网格数量的增加，目标声压的计算结果逐渐增大，但变化趋势逐渐变小，而网格质量呈现先升高后降低的趋势，计算时间从208 s延长到1 421 s. 兼顾计算时间和计算精度，本文中采用数量108 809和自由度304 695的网格进行计算，此时的网格质量也达到了最优(0.961 2).

表3 网格参数的选择及影响Table 3 Selection and influence of mesh parameter

在设置材料参数、求解域和边界条件后，可对模型进行求解分析，具体计算流程如图17所示. 在模型建立过程中，将压电陶瓷和水域交界处(橙色实线)设置为“端子”(交变电压终端电路)，同时也作为声波发射入口，而完美匹配层作为声波出口；将压电陶瓷另一端(紫色实线)设置为“接地”，同时施加“辊支承”状态；水域和完美匹配层域的外边界(蓝色实线)设置为“硬声场边界”；在摩擦副与水域交界处(红色实线)分别设置上/下摩擦副阻抗值.

Fig. 17 Solution process and boundary condition of the model图17 模型求解流程及边界条件设置

4.3.2 结果分析

根据超声波在润滑剂中的传播速度，计算得到声波到达图16上阻抗边界、下阻抗边界、反射信号接收边界和透射信号接收边界的时间分别为t1=6.7568 μs、t2=7.0946 μs、t3=8.1081 μs、t4=8.4459 μs. 反射信号接收边界的设置是为了接收图1中的反射信号b2，而透射信号接收边界的设置是为了接收图1中透射信号a1.图18给出了配副为铝/玻璃时不同时刻的超声波声压分布云图，4个子图分别对应时刻t1、t2、t3和t4，纵坐标为声压值(单位Pa). 随着超声波在传播介质中的反射和透射，由于传播过程中的损耗问题，出现声压逐渐衰减的现象，即图16中反射信号边界和透射信号边界接收处的超声波信号明显弱于上阻抗边界和下阻抗边界处的超声波信号. 声压分布云图难以直观分析配副方式对不同时刻声压分布的影响，因此需要进一步对不同时刻(或不同边界)的声压曲线进行提取.

Fig. 18 Surface acoustic pressure distribution at different times图18 不同时刻的表面声压总分布图

超声波在4个边界处的声压分布曲线如图19所示.结合图19(a)和(b)可知，虽然配副不同，但由于上摩擦副材质都为铝，故超声波在上阻抗边界和下阻抗边界的入射声波声压分布完全一致. 超声波为纵波传递方式，强度较高的声压处于压电陶瓷片的3 mm宽度范围内[即图19(a)和(b)中紫色框内的部分]，且随着横向距离的增加，声压逐渐趋近于0. 图19(c)和(d)表明随着下摩擦副阻抗值的增大，润滑剂-下摩擦副界面的反射系数越大，透射声波的声压值越小，即透射信号接收边界的声压越小[图19(d)]，反射信号接收边界的声波压力增强[图19(c)]，而反射声波b2蕴含了膜厚的信息，超声探头接收更高能量的b2声波，因此测量的膜厚范围也就越大，这是3.2部分铝/不锈钢配副时膜厚测量范围最大的根本原因.

Fig. 19 Acoustic pressure distribution curves at different boundaries图19 各边界处的声压分布

4.4 不同润滑剂时的声波传递仿真

4.4.1 建立模型

超声波在不同润滑剂内部的传播速度具有显著差别，因此会导致润滑剂内部的声压分布不同，本部分建立了如图20的仿真模型来研究不同润滑剂时声压分布规律. 压电声学为流体域，流体分别设置为水、1#润滑油和2#润滑油. 设置阻抗边界的材质为304不锈钢，时间步长设置为(0，T0/20，15 μs). 网格划分及其局部放大结果如图20(b)所示.

4.4.2 结果分析

不同润滑剂时4个边界处的声压分布情况如图21所示. 上阻抗边界处的入射声波声压与润滑剂阻抗呈正比关系[图21(a)]，即水作润滑剂时的入射声波声压是最高的. 而且，下阻抗边界的入射声波声压[图21(b)]、反射信号接受边界声压[图21(c)]和透射信号接受边界声压[图21(d)]都具有上述规律. 超声波从上阻抗边界传播到下阻抗边界的过程中，水、1#润滑油和2#润滑油的声压峰值衰减量分别为80.79%、83.78%和87.39%.相比其他2种润滑剂，2#润滑油的声压衰减幅度最大，这是因为上摩擦副-润滑剂分界面的反射系数随润滑剂的声阻抗减小而增大，致使反射信号(即图1中声波b1)增强，而透射信号减弱，最终使得下阻抗边界处的入射声波声压信号衰减加剧. 从图21(c)可知，2#润滑油作为润滑剂时的反射信号声压(即图1中声波b2)最低，在压电陶瓷宽度(3 mm)内的声压范围为(0.56~1.14 Pa)，显著小于水时的声压范围(1.92~3.83 Pa)及1#润滑油时的声压范围(1.10~2.20 Pa)，这是3.3部分的试验中2#润滑油时膜厚测量范围最小的内在原因.

Fig. 21 Acoustic pressure distribution with different lubricants图21 不同润滑剂时各边界处的声压分布

5 结论

为实现动态条件下宽范围润滑膜厚度的实时监测，本文中搭建了1套基于LabVIEW的膜厚在线超声测量系统，提出了1种弥补测量盲区的复合模型，探讨了配副方式和润滑剂种类对测量盲区的影响，结论如下：

a. 基于自主搭建的实时测量系统对4种动态变化膜厚进行了测量，发现矩形波膜厚的跟踪效果最好，而锯齿波膜厚跟踪效果最差；在有效带宽(-12 dB)外侧，反射系数曲线可能会出现环境噪声导致的伪共振点.

b. 下摩擦副材料的声阻抗越大，膜厚测量范围越大，且测量盲区越小. 随着润滑剂声阻抗的减小，测量范围呈现减小趋势，而测量盲区逐渐增大. 本文中提出的复合模型结合其他2种模型可实现单个探头对宽范围膜厚的全域测量.

c. 利用仿真模型研究了配副和润滑剂对声波传递规律的影响. 发现下摩擦副或润滑剂的声阻抗增大时，蕴含膜厚信息的反射波b2能量也增大，从而降低了膜厚的测量盲区.