基于改进压缩采样匹配追踪算法的机械振动信号恢复

李一飞， 王桂宝， 李伟， 王磊， 杨坤， 王楠

（陕西理工大学机械工程学院， 陕西汉中 723001）

0 前言

现代大型机电设备通常包含众多旋转机械结构，滚动轴承作为核心部件， 其健康程度影响旋转机械的稳定性［1］。 当滚动轴承产生故障时， 会导致整个机械设备运行效率降低， 甚至发生重大的生产事故［2］。 因此机械设备故障诊断与监测十分必要。 在滚动轴承的故障诊断与检测中， 会产生大量的机械信号数据， 而且振动信息采集必须遵守奈奎斯特采样定理。 该定理要求采样频率远大于被测频率， 至少是其最高频率的2 倍。 DONOHO 等［3－5］提出压缩感知， 该理论可以用更小的采样率对信号进行采样， 受到了医学［6］、 雷达［7］、 遥感图像［8］等方面的高度关注。

压缩感知理论中主要研究重构算法和传感矩阵的构造， 其中传感矩阵包括设计观测矩阵和稀疏表示。信号的稀疏表示是指信号可以在稀疏域中用几个较少的非零点表示， 使用创建的观测矩阵对信息降维处理，然后采用重建方法将信号信息重新恢复。 目前传统的重构算法可以划为3 类： 组合类算法、 凸优化算法和贪婪匹配追踪算法［9］。 3 种方法各有优缺点： 组合算法要求观测的样本数量最多， 但是计算效率最好； 凸松弛算法计算量最大， 但是在观测数目较少时才获得高的重构精度； 贪婪匹配算法对计算数量和准确度需求居中， 它也是3 种重建算法中使用最广泛的。 现有的贪婪匹配追踪算法有匹配追踪（Matching Pursuit，MP） 算 法［10］、 正 交 匹 配 追 踪（Orthogonal Matching Pursuit， OMP） 算法［11］、 分段正交匹配追踪（Stagewise Orthogonal Matching Pursuit， StOMP） 算法［12］、 压缩采样匹配追踪（Compressing Sampling Matching Pursuit，CoSaMP） 算 法［13］、 广 义 正 交 配 追 踪 （Generalized Orthogonal Matching Pursuit， GOMP） 算法［14］等。

在压缩感知中， 重构算法极为重要， 其性能将影响机械振动信号的恢复重构。 本文作者通过对比OMP 算法、 GOMP 算法、 CoSaMP 算法以及改进的CoSaMP （IO⁃CoSaMP） 算法应用于机械信号的恢复效果， 并分析重构概率和重构误差， 以期在工程实际中起到指导性作用。

1 压缩感知理论

1.1 基本理论

压缩感知理论重构的基本条件是： 所测得信号稀疏或者可以在变换域将其稀疏表现出来， 即原信号在稀疏区域只有几个不为零的量， 而剩下的大多数为零或者接近零； 信号通过观测矩阵投影， 从高维投射到低维， 最后利用少量的观测值通过重构或者计算重现原始信号。

设信号x为一维信号， 具有稀疏度K， 其长度为N， 令Ψ为信号稀疏基矩阵， 即Ψ为N×N的稀疏矩阵，θ则是稀疏系数。 那么x可以表示为

观测向量y由观测矩阵ϕ和测量信号x得到，ϕ是M×N（M≪N） 的测量矩阵， 观测数为M。 使A＝ϕΨ，A被叫做感知矩阵， 观测向量为y（M×1） 可以用式（2） 表示：

y＝ϕψθ＝Aθ＝ϕx（2）

由于观测矩阵ϕ的M≪N， 方程（2） 为欠定方程， 未知数的个数多而方程的个数少， 导致方程的解不唯一， 不能准确地重构出原始信号。 针对这个问题， 发现当具有K稀疏的向量z， 观测矩阵ϕ必须满足限制等距规则［15］（RIP）， 即

其中，ε＞0。 由于x有一定的稀疏度， 且ϕ满足限制等距规则， 可以把解不唯一的问题转化为L0 范数的最优化问题， 即：

由于最小L0 范数优化求解存在NP－hard 问题，求解非常困难而且数值不够稳定， 文献［16］指出求解最小L0 范数的优化问题可以转化为L1 范数的优化问题， 即

根据公式（2） 可知： 为了得到稀疏系数θ需要利用观测向量y、 观测矩阵ϕ和稀疏基矩阵Ψ， 然后利用公式（1） 的稀疏矩阵与稀疏系数得到原始信号x。 用于信号压缩感知重构的方法有很多， 贪婪匹配追踪类算法的优点在于复杂度低、 计算量小和重构概率高， 所以得到了广泛的应用。

1.2 压缩采样匹配追踪算法及改进算法

压缩采样匹配追踪 （CoSaMP） 算法以ROMP（Regularized Othogonal Matching Pursuit） 算法为基础进行的改进， 较大程度上提升了重构准确度， 同时还延续了匹配追踪类算法的优势， 拥有相对较低的计算复杂性， 是一个理想的重构算法。 CoSaMP 算法同时也对OMP 算法做出改进， 迭代时需要选取多个原子，但除去原子之间的选取要求之外， 它与ROMP 的唯一区别就是： ROMP 每次迭代中选择的原子不会被丢弃， 而CoSaMP 算法每次迭代中选择原子的方式是取其精华去其糟粕， 即保留正确原子并且删除错误原子。 CoSaMP 算法利用了回溯思想， 每一次迭代都会不断地增加新的原子， 同时还会剔除掉上一次的错误原子， 从而使其重构准确率得到提高， 其成功重构依赖于观测值很多的情况。 针对以上问题提出的IOCo⁃SaMP 算法的流程如图1 所示。

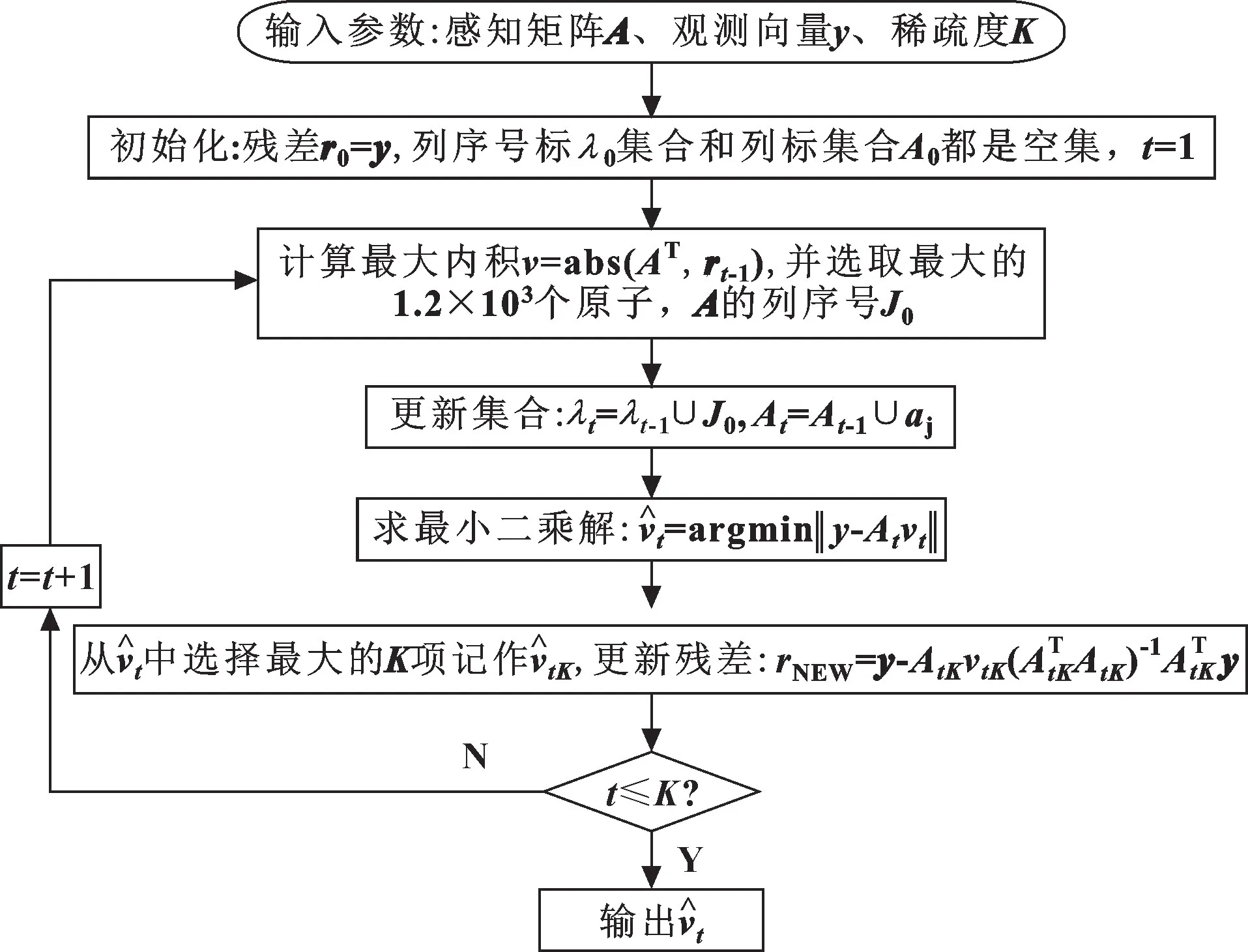
图1 IOCoSaMP 算法流程Fig.1 Algorithm flow of IOCoSaMP

观测值数目相同时， 重构率会随着稀疏度的增加而不断降低； 稀疏度相同时， 重构率会随着观测值的增加而提高， 但是观测的数目越多则重构时间越长。基于此， 作者改进了压缩采样匹配追踪算法。 由于太多的原子数会增加错误原子被选中的概率， 合适的原子数非常重要， 所以将原子数定为1.2×103个。 通过大量实验验证， 当原子数为1.2×103个时， 算法具有很好的重构性能， 1.2×103个原子既可以节省重构的时间， 还能够保证其重构精度。 利用仿真信号和实测轴承振动信号发现： 与同类算法相比， 在相同的重构概率下， 该算法所需的观测值更少， 稀疏度更高。

2 仿真实验结果分析

通过仿真信号与实测滚动轴承信号验证新算法的性能， 对比不同算法在观测值和稀疏度变化过程中重构概率的变化， 再用实测信号的重构误差来衡量算法的性能。 实验环境： 将新算法应用到64 位Windows10操作系统上， 运行内存为8 GB， 在MATLAB2016a 上运行。 为了证明算法的有效性， 对比OMP、 StOMP、ROMP、 gOMP、 CoSaMP 和IOCoSaMP 算法在不同稀疏程度下和不同观测值下的重构可能性。 结果显示：该方法在相同的重构概率下所需的观测数目更少， 但稀疏度却可以更大。

2.1 仿真数据验证

使用一维随机信号作为实验对象x∈RN， 观测矩阵选择高斯随机矩阵，N＝256， 观测值M＝130， 缺失了126 个数据点， 对信号以稀疏化的方式进行采样离散余弦变换， 稀疏度取40， 设ε＝10－6算法迭代停止， 重构误差e表达式如下：

采用一维随机信号验证IOCoSaMP 算法， 结果如图2 所示。 从图2 （d） （e） 可以看出： 改进算法的重构误差不高于0.766， 而未改进算法的重构误差不高于1.132， 改进算法的重构误差小， 可以很好地重构出原始信号， 具有很好的重构性能。

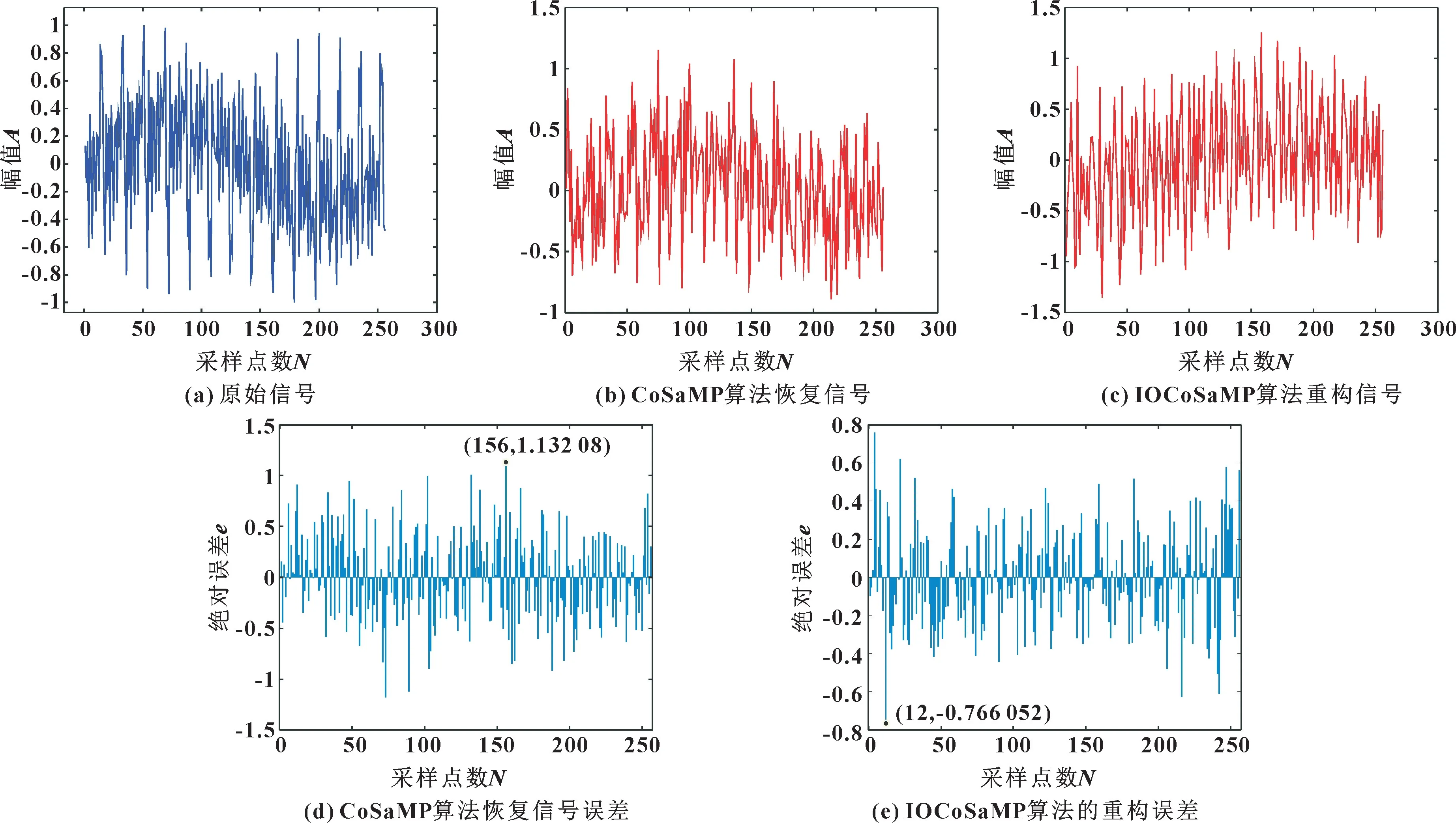
图2 一维随机信号重构结果Fig.2 1D random signal reconstruction results： （a） original signal； （b） restoring signal of CoSaMP algorithm； （c）reconstructed signal of IOCoSaMP algorithm； （d） restoring signal error of CoSaMP algorithm；（e） reconstructed signal error of IOCoSaMP algorithm

2.2 不同稀疏度下的重构概率

选取一维随机信号，M＝128、N＝256， 稀疏度在0～80 内， 步长为10， 重复实验1 000 次， 采用7种不同算法对同一个信号进行重构， 并测试了不同算法的重构概率随稀疏度的变化情况。 由图3 可知： 压缩采样匹配追踪算法与改进算法相比， 当稀疏度为50 时改进算法的重构概率可以达到100%， 而未改进算法的重构概率为0。

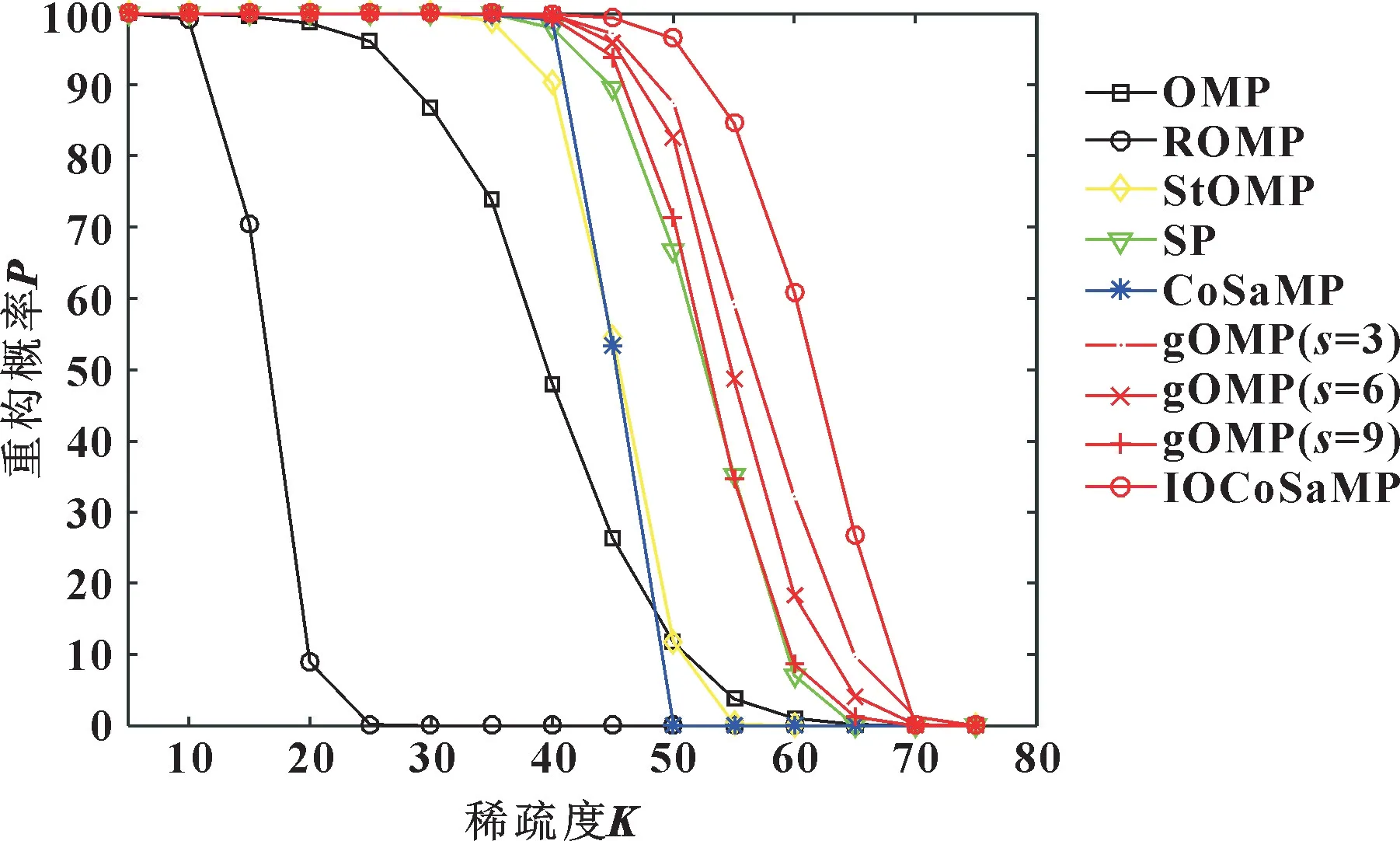
图3 不同算法的重构概率（不同稀疏度）Fig.3 Reconstruction probabilities of different algorithms（different sparsities）

2.3 不同观测值下的重构概率

选取一维随机信号作为实验对象，N＝256、K＝20， 观测值区间为［50， 110］， 步长为10， 每种稀疏度重复实验1 000 次， 通过比较5 种算法的重构效果， 测试不同算法的重构概率随观测值的变化情况。从图4 可以看出： 在相同观测值时， IOCoSaMP 算法的重构概率高于其他算法， 并且当几种算法的重构概率相同时， 改进算法所需的观测值小于同类算法。

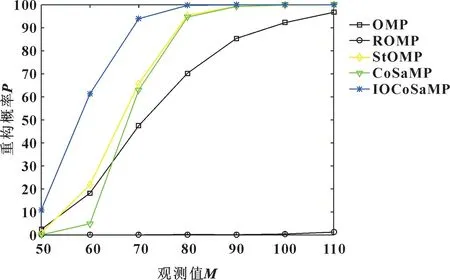
图4 不同算法的重构概率（不同观测值）Fig.4 Reconstruction probabilities of different algorithms（different observation values）

2.4 算法的性能比较

从图4 可以得出： 当稀疏度相同时， 随着观测值的增加， 重构概率相应提高， 改进算法的重构概率高于其他的算法。 当观测值为80 时， 利用IOCoSaMP算法可以达到100%的重构， StOMP 与CoSaMP 算法的观测值为90 时才可以达到和改进算法一样的效果，而OMP 需要更多的观测值。 图5 是将前面所述的仿真结果保存下来， 单独对比改进算法与OMP、gOMP、 CoSaMP 算法的性能， 改进的算法相较于OMP 和gOMP 以及CoSaMP 具有更高的重构概率、 更好的恢复效果。

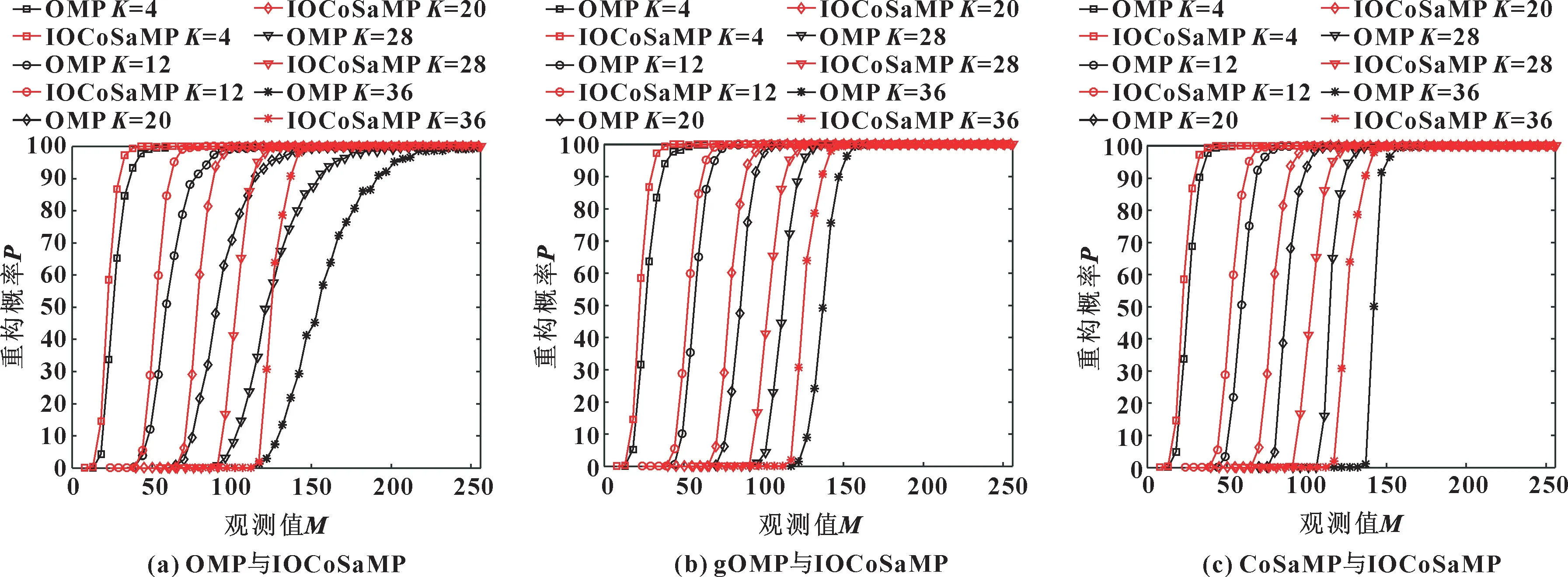
图5 算法间的对比Fig.5 Comparison between algorithms： （a） OMP and IOCoSaMP； （b） gOMP and IOCoSaMP； （c）CoSaMP and IOCoSaMP

2.5 实验

采用实测振动信号验证算法的重构能力。 滚动轴承的振动信号来源于美国西储大学的轴承数据， 设x∈RN（N＝1 000）为实测轴承正常运行时的时域振动信号（实验轴承为6205⁃2RS JEK SKF 深沟球轴承，采样频率12×103Hz， 转速1 797 r/min， 负载754.7 W）。 从数据中取一段信号， 通过对比原始信号用CoSaMP 算法以及用改进算法恢复出的信号的重构误差来验证算法的有效性。

由图6 可知： 压缩采样匹配追踪算法的重构误差最高不超过0.176 8， 改进的压缩采样匹配追踪算法的误差最高不超过0.125 2， 重构误差降低了0.05，具有良好的重构性能。

图6 算法的重构误差验证Fig.6 Verification of the reconstruction error of the algorithm： （a） original signal； （b） missing signal； （c） restoring signal of CoSaMP algorithm； （d） restoring signal of IOCoSaMP algorithm； （e） reconstructed signal error of CoSaMP algorithm； （f） reconstructed signal error of IOCoSaMP algorithm

3 结论

文中提出的改进压缩采样匹配追踪算法选择更少的候选原子， 可以节省原子候选的时间， 降低错误原子被选中的概率。 仿真信号与实测轴承信号的仿真实验结果表明： 相同的稀疏度下， 所提算法的重构概率高于其他算法， 相同的观测值下， 改进算法较其他算法的重构概率高， 并且重构误差降低了0.05， 说明IOCoSaMP算法具有不错的重构效果和一定的应用价值。