带参数集值向量优化问题ε-强有效点集的连通性

徐梦豪,章 勤 ,朱 彬

(1.赣东学院基础部,344000,江西,抚州;2.抚州市第二实验学校数学组,344000,江西,抚州)

0 引言

近几年,强有效点集一直被众多学者研究,Cheng[1]1999年通过局部凸空间引入了强效率,并证明了强有效点的存在性,以及强有效点的稠密性。同年武育楠等[2]在锥类凸集值映射下提出强有效性,并在这个条件下通过系统地研究从而得到了强有效点集的另一种也就是连通性的结果。几年后,赵春英等[3]利用基泛函得到了ε-强有效点集以及ε-严有效点集的标量化定理。2010年王其林[4]对标量化定理的研究得到完善,得到了在近似锥次凸集值映射下向量优化问题ε-强有效点的标量化定理。2012年陈剑尘等[5]在弧连通集值映射下,证明了集值映射在约束条件下依然是弧连通的,并研究了含约束条件Henig有效解集的连通性。2015年余丽[6]不仅提出了ε-强有效次微分的存在性,还在此基础上研究了它的稳定性,并建立了最优性条件。

目前,关于强有效解的连通性大部分是在带约束或无约束映射下研究的,在参数扰动下的ε-强有效点集的连通性目前还未发现有学者研究。ε-强有效点集的连通性已经在文献[3]中给出了证明,因此,本文在这些研究基础上进行了一些改进以及推广。在目标集值映射为弧连通的,且可行域为弧连通紧的情况下,证明了在参数扰动下的ε-强有效点集的连通性。

1 基本知识

在本文后续的研究中,X,Y,Z均为局部凸的Hausdorff拓扑线性空间。Y*为Y的拓扑对偶空间,N(0)为Y的零点邻域基。C⊂Y为具有非空内部的点闭凸锥,定义C的正对偶锥C*:={φ∈Y*:φ(y)≥0,∀y∈C},拟内部C#:={φ∈Y*:φ(y)>0,∀y∈C{0}}。D⊂Y为非空子集,cl(D)、int(D)、cone(D)分别为D的闭包、内部、生成锥,并定义生成锥cone(D):={λθ:λ≥0,θ∈D}。

锥C的凸子集B称为C的基,若满足2个条件:

1)0≠cl(B);

2)C=cone(B)={σb:σ≥0,b∈B}。

设B是C的一个基,定义基泛函Bst={φ∈Y*:∃α>0,∀b∈B,φ(b)≥α}。

引理1[1]:若B是C的基,则Bst有以下几种性质:

1)∅≠Bst⊂C#⊂C*;

2)Bst+C*=Bst;

3)设φ∈Y*,则φ∈Bst时,对于∀u∈U,∀b∈B,φ(u-b)≤0想要成立只能是U为Y的零点凸邻域;当U为零点的平衡凸邻域时,φ(u+b)≥0成立;

4)若B是C的有界基,φ∈Bst,则对于∀φ∈Y*,存在自然数n,使得φ-φ/n∈C*;

5)int(C*)⊂Bst,若B有界,则Bst=int(C*)。

定义1[7]:若∀x1,x2∈A,存在连续映射ηx1,x2:[0,1]→A,使得ηx1,x2(0)=x1,ηx1,x2(1)=x2,则集合A⊆X被称为弧连通的。

定义2[8]: 设A⊆X是非空的弧连通集,若对于∀x1,x2∈A,t∈[0,1],有(1-t)F(x1)+tF(x2)⊆F(ηx1,x2(t))+C,则称集值映射F:A→2Y为C-弧连通的。

若对于∀x1,x2∈A,t∈[0,1],有(1-t)F(x1)+tF(x2)⊆F(ηx1,x2(t))-C,则称集值映射F:A→2Y为(-C)-弧连通的。

引理2[9]:设X1,X2…Xn均为弧连通空间,则积空间X1×X2×…×Xn也是弧连通空间。

定义3[10]:假设X,Y为拓扑空间,称集值映射F:X→2Y在x0→X处为上半连续的,若对于F(x0)的任意邻域V⊂Y,存在对应点x0的邻域U,使得F(x)⊂V,∀x∈U,若F对于∀x∈X都上半连续,则称F在X上上半连续。

引理3[10]:很显然,如果F和G都是连续的,那么G·F也为连续的。

引理4[11]:如果H(U)满足以下几个条件:

1)U⊆X为非空的连通集;

2)对于∀u∈U,连通集H(u)非空;

3)集值映射H:U→2Y在U上是上半连续的。

则H(U)是连通集。

引理5[12]:令X,Y是Hausdorff拓扑空间,当X是紧的,集值映射F:X→2Y上半连续,且对于任意的x∈X,F(x)为紧的,则F(X)是紧的。

引理6[9]:设X是局部凸空间,则A⊂X有界的充分必要条件是A⊂XW有界,其中XW为X上弱拓扑相应的局部凸空间。

2 带参数的ε-强有效点集的连通性

设E⊂X,Λ⊂Z分别为非空子集,集值映射H:Λ→2E,含有参数λ∈Λ的集值映射F:E×Λ→2Y,且对于∀x∈E,∀λ∈Λ,F(x,λ)≠∅,H(λ)≠∅。

考虑以下带参数的集值向量优化问题(PVP):

令F(H(λ),λ)=∪x∈H(λ)F(x,λ),且无特别说明,∀λ∈Λ,F(x,λ)均定义在H(λ)上。

定义4[3]:设ε∈C,B是C中的有界基,如果满足∀φ∈Y*,∃U,V∈N(0),使得实数集合

φ(cl(cone(D+ε-y))∩(U-cone(V+B)))

是有界的,则称y∈D为D的关于锥C的ε-强有效点,记为y∈ε-GE(D,C)。

定义5:设x0∈H(λ),C⊂Y且为具有有界基B的点闭凸锥,N(0)为Y中的零点邻域基,y0∈F(x0,λ),若∃U,V∈N(0),使得

φ(cl(cone(F(H(λ),λ)+ε-y0))∩(U-cone(V+B)))

有界,则称x0∈H(λ)为(PVP)中的含参ε-强有效解,y0∈F(x0,λ)为(PVP)中的含参ε-强有效点,并用ε-GE(F(H(λ),λ),C)表示(PVP)中的全体含参ε-强有效点。

定义6[4]:设φ∈Y*{0},x0∈D,ε∈C,(x0,y0)称为(VP)的近似最优元,如果存在y0∈F(x0),使得φ(y0)≤φ(y)+φ(ε),∀y∈F(D)。

引理7[13]:当集值映射F:A→2Y是C-弧连通的,则F(A)+C为凸集。

引理8[3]:设C是弱拓扑Y上的正规锥,D是空间Y中的凸集,那么y0∈ε-GE(D,C)当且仅当对于任意的φ∈Y*,∃φ∈C*,使得φ∈φ+Bst,φ(y0)=min{φ(y)+φ(ε):y∈D}。

注1文[14]中有指出C具有有界基是C为正规锥的一个充分条件,故当C具有有界基时,C必为正规锥。

定义7[3]:对于固定的φ∈Y*,集合D的ε-极小点集定义为

ε-S(D,φ)={y*∈D:φ(y*)}=min{φ(y)+φ(ε):y∈D}.

引理9[3]:设B是C的有界基,则对于任意的c∈C,φ∈Bst有φ(c)≥0。

引理10[3]:D⊂Y,φ∈Bst,若C是Y中的点闭凸锥,则ε-S(D,φ)⊂ε-S(D+C,φ),当y∈ε-S(D+C,φ)且y∈D时有y∈ε-S(D,φ).若D为Y中的凸集,则对于∀φ∈Bst,ε-S(D,φ)为凸集。

引理11[3]:设Bst是C的有界基,D是Y中的凸集,则y0∈ε-GE(D,C)当且仅当存在φ∈Bst使得y0∈ε-S(D,φ),即ε-GE(D,C)=∪φ∈Bstε-S(D,φ)。

命题1:设B为C中的有界基,D为凸集且弱紧,则ε-GE(D,C)≠∅。

证明：要证明ε-GE(D,C)≠∅,只需证明存在x0∈ε-GE(D,C)即可。由于B为C中的有界基,根据注1可得C为正规锥,因此,由引理8,∀φ∈Y*,会存在φ∈C*,使得φ∈φ+Bst,φ(y0)=min{φ(y)+φ(ε):y∈D}。

假设∃φ∈Bst,因D为弱紧集,故∃x0∈D使得φ(x0)=min{φ(x)+φ(ε):x∈D},根据引理1中4),∀φ∈Y*,存在一个自然数n,使得nφ-φ∈C*,又由于φ∈Bst,故nφ-φ+φ∈C*+Bst=Bst,即(n+1)φ∈φ+Bst,由此可知x0∈ε-GE(D,C)。

命题2:设X,Y,Z是局部凸Hausdoff拓扑线性空间,C为Y中的闭凸点锥且具有有界基B,E⊂X,Λ⊂Z均为非空的弧连通集。同时E为紧子集。F:E×Λ→2Y是C-弧连通的且上半连续的集值映射(Y上的拓扑为弱拓扑σ(Y*,Y)),F在E×Λ上取弱紧值,H:Λ→2E是集值映射,且∀λ∈Λ,H(λ)是非空的弧连通紧子集。则∀λ∈Λ,ε∈C,ε-GE(F(H(λ),λ),C)是非空的连通集。

证明：证明分为2部分,第1部分证明ε-GE(F(H(λ),λ),C)非空。

因为集值映射F:E×Λ→2Y为上半连续的,故F:H(λ)×{λ}也是上半连续的。又因为F在E×Λ上取弱紧值,故F在H(λ)×{λ}上也取弱紧值,根据引理5可知F(H(λ),λ)为弱紧集,即F(H(λ),λ)是空间(Y,σ(Y*,Y))上的紧集。而F(H(λ),λ)是C-凸集,因此F(H(λ),λ)是凸的弱紧集,且C具有有界基B,由命题1可知ε-GE(F(H(λ),λ),C)≠∅,∀λ∈Λ。

第2部分证明ε-GE(F(H(λ),λ),C)的连通性,为方便证明,根据引理11转为证明∪φ∈Bstε-S(F(H(λ),λ),φ)的连通性,再根据引理4进行证明,因此需先证明ε-GE(F(H(λ),λ),C)=∪φ∈Bstε-S(F(H(λ),λ),φ)。

由于E,Λ均为弧连通集,根据引理2可知E×Λ为弧连通集,同理H(λ)×{λ}也为弧连通集。又因为集值映射F在E×Λ上为C-弧连通集,故F在H(λ)×{λ}也为C-弧连通集,由引理7可知F(H(λ),λ)+C为凸集。已证得ε-GE(F(H(λ),λ),C)≠∅,因此∃φ∈Bst,使得ε-S(F(H(λ),λ),φ)≠∅,根据引理11可知ε-GE(F(H(λ),λ),C)=∪φ∈Bstε-S(F(H(λ),λ),φ)。

接下来证明∪φ∈Bstε-S(F(H(λ),λ),φ)的连通性。定义集值映射l:Bst→2F(H(λ),λ),l(φ)=ε-S(F(H(λ),λ),φ),则

l(φ)={y*∈F(H(λ),λ):φ(y*)=min{φ(z):z∈F(H(λ),λ)}},

其中φ(z)=φ(y)+φ(ε),y∈F(H(λ),λ)。

根据引理4分以下3个小部分进行证明:

1)证明Bst⊂Y*为非空的连通集。

根据凸集与连通集的定义可知凸集必为连通集,为了证明Bst为连通集,所以只需证明Bst为凸集。又由于定义可知Bst为基泛函,从凸集的定义可知基泛函一定是凸集,即得证。根据引理1, 1)知Bst≠∅,所以Bst⊂Y*为非空的连通集。

2)证明∀φ∈Bst,l(φ)为连通集。

设∀x1,x2∈l(φ),存在y1∈F(x1),y2∈F(x2),使得

φ(y1)≤φ(y)+φ(ε),φ(y2)≤φ(y)+φ(ε),∀y∈F(H(λ),λ).

(1)

由于H(λ)是弧连通集,故存在一个连续映射ηx1,x2:[0,1]→H(λ),使得ηx1,x2(0)=x1,ηx1,x2(1)=x2。

又因为F(x,λ)在H(λ)上是弧连通的,故

ty1+(1-t)y2∈tF(x1)+(1-t)F(x2)⊆F(ηx1,x2(t))+C,

∀t∈[0,1],∃c∈C,yt∈F(ηx1,x2(t)),使得ty1+(1-t)y2=yt+c,由c∈C,φ∈Y*及式(1)可知,∀y∈F(H(λ),λ)有

φ(yt)≤φ(yt+c)=tφ(y1)+(1-t)φ(y2)≤φ(y)+φ(ε).

故∀t∈[0,1],有ηx1,x2(t)∈l(φ),因此l(φ)为凸集,即为连通集。

3)证明集值映射l:Bst→2F(H(λ),λ)在Bst上是上半连续,即l(φ)在Bst为上半连续。

由于F(H(λ),λ)为紧集,从而易知对于∀φ∈Bst,l(φ)≠∅(其中Bst上的拓扑为强拓扑β(Y*,Y))。假设l在Bst上不是上半连续的,则存在φ0∈Bst,使得l在φ0上不是上半连续的。根据定义3可知存在l(φ0)的邻域V,使得对φ0的任意邻域U,都存在φ∈U∩Bst,满足l(φ)⊄V。以及存在网{φα:α∈Λ}⊂Bst,使得φα∈U∩Bst,满足φα→φ0(关于强拓扑β(Y*,Y)),且l(φα)⊄V,∀α∈Λ。故存在网{xα:α∈Λ},有

xα∈l(φα),xα∉V,∀α∈Λ.

(2)

由于l(φα)≠∅,可以取yα使得yα∈l(φα)⊂F(xα),有

φα(yα)≤φα(z)+φα(ε),∀z∈F(H(λ),λ).

(3)

由于F(H(λ),λ)为弱紧集,取收敛网{yα},则有yα→y0∈F(H(λ),λ),又因为H(λ)为紧集,设xα→x0。又因为F是上半连续,所以y0∈F(x0)。设L=F(H(λ),λ),定义PL(y′)=sup(y′(z)+y′(ε)|:z∈F(H(λ),λ)),y′∈Y*,其中PL为Y*上的连续半范。∀δ>0,由于φα→φ0,∃α0,当α≥α0时,有

PL(φα-φ0)=sup{|φα(z)+φα(ε)-φ0(z)-φ0(ε)|:z∈F(H(λ),λ)}<δ.

即|φα(z)+φα(ε)-φ0(z)-φ0(ε)|<δ,∀z∈F(H(λ),λ),∀α≥α0,且∀α≥α0,有

|φα(yα)-φ0(yα)|<δ.

(4)

又因为yα→y0,φ0∈Y*,故∃α1≥α0∈Λ,使得

|φ0(yα)-φ0(y0)|<δ,∀α≥α1.

(5)

综合式(4)和(5)可得,∀α≥α1,有

φα(yα)-|φ0(y0)|≤|φα(yα)-φ0(yα)|+ |φ0(yα)-φ0(y0)|≤δ+δ=2δ.

根据引理4及上述证明能得出ε-GE(F(H(λ),λ),C)为连通集。

定理1:设X,Y,Z是局部凸Hausdoff拓扑线性空间,C为Y中的闭凸点锥,B是C的基且有界,E⊂X,Λ⊂Z均为非空的弧连通紧子集。F:E×Λ→2Y是C-弧连通的集值映射且连续(Y上的拓扑为弱拓扑σ(Y*,Y)),F在E×Λ上取弱紧值,H:Λ→2E也是连续的集值映射,且∀λ∈Λ,H(λ)是非空的弧连通紧子集。同时,∀λ∈Λ,ε∈C,ε-GE(F(H(λ),λ),C)=∪φ∈CΔε-S(F(H(λ),λ),φ)(其中CΔ⊂Bst为关于强拓扑β(Y*,Y)的紧子集),则∪λ∈Λε-GE(F(H(λ),λ),C)是非空的连通集。

证明：首先命题2已证得∀λ∈Λ,ε-GE(F(H(λ),λ),C)≠∅,故

∪λ∈Λε-GE(F(H(λ),λ),C)≠∅.

再证∪λ∈Λε-GE(F(H(λ),λ),C)的连通性,定义集值映射Ω:Λ→2Y,使得

Ω(λ)=ε-GE(F(H(λ),λ),C).

由命题2已知ε-GE(F(H(λ),λ),C)是连通集,故Ω(λ)是连通的,又因为Λ是弧连通的,因此Λ也是连通的,根据引理4,只需再证得Ω:Λ→2Y是上半连续的即可证明∪λ∈Λε-GE(F(H(λ),λ),C)是连通集。

使用反证法证明,假设∃λ0∈Λ,使得映射Ω不是上半连续的。则存在Ω(λ0)的弱开邻域V′,以及网{λτ:τ∈Γ},满足λτ→λ0,且有Ω(λτ)⊄V′,∀τ∈Γ。故存在网{yτ:τ∈Γ},使得

yτ∈Ω(λτ),yτ⊄V′,∀τ∈Γ.

(6)

因为CΔ是紧的且网{φτ}⊂CΔ,故假设∃φ0∈CΔ使得φτ→φ0。由于F(x,y)和H(λ)是连续的集值映射,则F(x,y)和H(λ)均上半连续且下半连续,根据引理3可知∀λ∈Λ,F(H(λ),λ)上半连续且下半连续,因此∀h0∈F(H(λ0),λ0),∃hτ∈F(H(λτ),λτ),满足hτ→h0。又因为yτ∈Ω(λτ),因此∃fτ∈CΔ,使得yτ∈ε-S(F(H(λτ),λτ),φτ),根据定义6,∀hτ∈F(H(λτ),λτ),有

φτ(yτ)≤φτ(hτ)+φτ(ε).

(7)

根据命题2证明已知F(H(λ),λ)是弱紧的,因此F(H(λ0),λ0)也是弱紧的。又由于F(H(λ),λ)是上半连续的,因此假设∃y0∈F(H(λ0),λ0),使得yτ→y0。设R=∪λ∈ΛF(H(λ),λ),易知R也是弱紧的,且弱有界,由引理6可知R为有界集。定义MR(y*)=sup{|y*(hτ)+y*(ε)|:hτ∈F(H(λ),λ)},y*∈Y*,其中MR为Y*上的连续半范。由φτ→φ0可知,∃τ0∈Γ,当∀τ≥τ0时,有

MR(φτ-φ0)=sup{|φτ(hτ)+φτ(ε)-φ0(hτ)-φ0(ε)|:hτ∈F(H(λ),λ)}<θ.

故∀hτ∈F(H(λ),λ),∀τ≥τ0,有|φτ(hτ)+φτ(ε)-φ0(hτ)-φ0(ε)|<θ。由式(7)得

|φτ(yτ)-φ0(yτ)|<θ,∀τ≥τ0.

(8)

又由于yτ→y0,故∃τ1∈Γ,使得

|φ0(yτ)-φ0(y0)|<θ,∀τ≥τ1.

(9)

结合式(8)和(9),∀τ≥τ0,∀τ≥τ1,有

|φτ(yτ)-φ0(y0)|≤|φτ(yτ)-φ0(yτ)|+ |φ0(yτ)-φ0(y0)|≤θ+θ=2θ.

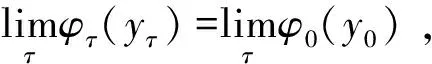
综上所述,根据引理4可知∪λ∈Λε-GE(F(H(λ),λ),C)为连通集。

3 结语

近似解的研究一直是众多学者所关注的问题,且强有效性是局部凸空间中超有效性和严有效性的推广,故ε-强有效点集的连通性具有很强的理论价值和现实意义。以往对于解的连通性都是在可行域为凸集、集值映射为无约束或带约束的条件下研究。本文在文献[3]的启发下,文献[6]的基础上,使其在参数的扰动下,可行域为弧连通的条件下,证明了含参数ε-强有效点集的连通性。由于凸集必然是弧连通的,弧连通不一定是凸集,因此,本文是对文献[3]的相关研究进行了适当的改进及推广。