不同载荷边界典型负泊松比结构等效力学建模

张 焘,王立民,周志坛,卞云龙,冯帅星,高 靖

(1.国防科技大学 空天科学学院, 长沙 410073; 2.中国航天科工集团有限公司六院四十一所, 呼和浩特 010010; 3.南昌航空大学 飞行器工程学院, 南昌 330000)

0 引言

超力学结构是指具有反常力学性能的结构[1],如当前最常见的负泊松比结构[2]。负泊松比结构受压缩后会表现出收缩而非膨胀的反常现象,收缩部分会导致结构致密化,从而提高结构的抗载能力;受拉伸载荷作用则会出现膨胀的反常现象,使得结构体积增大、抗断裂能力增强。负泊松比结构的力学现象通常称为负泊松比效应,其包括压缩-收缩现象和拉伸-膨胀现象,后者也称为拉胀效应[3]。负泊松比效应能带来缓冲吸能减震、抗剪切性能、曲面同向性等效应[4],被广泛应用为汽车、航空、航天及武器装备结构件。负泊松比结构的最大优势在于轻量化高抗力及可控的力学性能,是固体火箭关键结构的潜在方案,如发动机不规则外衬、曲面外壳及精密仪器减震底座等,能大幅提高固体火箭的运载能力。因此,开展负泊松比结构力学理论模型研究对其在固体火箭上的具体应用具有重要意义。

当前关于负泊松比结构的研究主要集中于新型结构的设计和应用、弹塑性等效理论力学模型的建立及结构负泊松比效应的有限元分析。Jiang等[5]设计了具有双弧形侧壁的内凹六边形金属负泊松比蜂窝结构,并基于LS-DYNA进行了爆炸冲击响应分析。Zhao等[1]基于内凹六边形结构设计了曲面负泊松比结构,并进行了简单的等效弹性力学理论建模、开展了有限元分析。Guo等[6]基于欧拉梁理论对内凹六边形结构和星形结构进行了等效弹性力学建模,获取了结构的等效泊松比和等效弹性模量,并通过有限元分析进行了验证。赵昌方等[7-8]针对内凹六边形多胞结构进行了准静态拉压和动态小球冲击数值研究,主要讨论了结构的负泊松比效应、力学特性及吸能效果。李功明等[9]采用能量法推导了内凹六边形结构泊松比的理论解。随着先进复合材料制备技术的发展,一些学者引入纤维复合材料设计了负泊松比结构[10-13],如具有超高比吸能效益的碳纤维增强复合材料[14],以实现结构轻量化和高性能优势的融合。然而,上述研究大多是数值模拟和实验研究,关于理论力学模型的研究较少、模型中设置的载荷边界条件较为单一,且未考虑横梁的变形情况。实际应用中,例如固体火箭的喷管和外壳,其载荷边界包括均布载荷、集中载荷及其他复杂载荷情况。

在增材制造技术的刺激下,越来越多的负泊松比结构被设计、制备和应用到各种工程领域。在这样的发展潜力下,负泊松比结构的理论力学研究显得更加重要,是结构设计和应用的基本指南,亟需进一步发展。内凹六边形结构是一类经典的双箭头结构,其结构简单容易制备、负泊松比效应有保障、可实现二维到三维的转化,是研究最广泛的一种超力学结构。为此,本文甄选内凹六边形结构为研究对象,基于欧拉梁理论建立了均布加载、平板加载和集中力加载情况下的负泊松比结构等效弹性模型,获取了结构几何参数对等效泊松比和等效弹性模量的影响规律,并通过有限元分析揭示了结构的变形特征、验证了理论模型的有效性。

1 等效力学理论建模

1.1 基本假设与几何结构

内凹六边形负泊松比结构代表性单元的几何模型见图1。其中,横梁长度L=35.25 mm,侧梁长度l=17.21 mm,内凹夹角为θ=75°,单元高度为H=33.25 mm,单元宽度为D=37.25 mm,单元厚度为Z=1 mm,单元的壁厚为t=1 mm;高度和宽度的几何关系分别为H=2lsinθ、D=2(L-lcosθ),材料为2024-T3铝合金。3种载荷边界(均布载荷、平板载荷、集中载荷)的示意如图1所示。p表示载荷大小。不同载荷边界将会产生不同的变形模式,从而影响结构的负泊松比效应和承载能力。当前的负泊松比结构大多采用各向同性材料(金属和聚合物)制备,这些材料的弹性和塑性阶段分明,且塑性段相对较长,对负泊松比效应的实现十分有用。基于Euler梁理论[4]和基本假设①材料变形处于弹性范围内,满足小变形假设;② 胞壁变形以弯曲为主,且不考虑轴向的拉伸和压缩,建立不同载荷边界下的等效弹性力学理论建模,具体推到过程及结论分别如下。

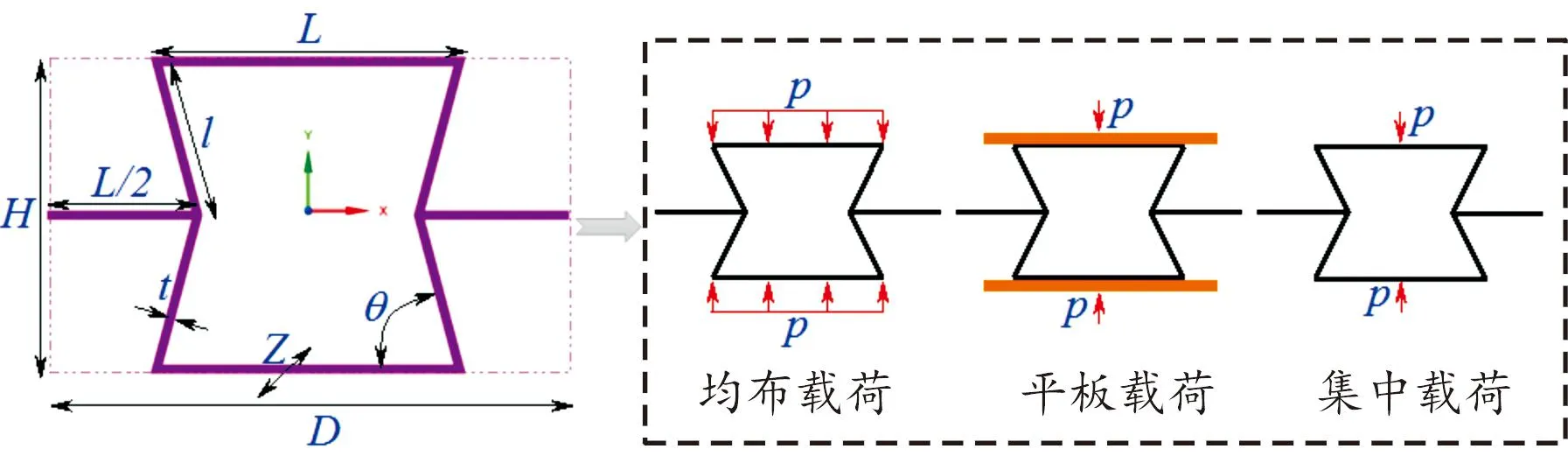
图1 内凹六边形结构几何模型及载荷边界

1.2 均布载荷边界

均布载荷加载时,取载荷集度p、材料的弹性模量E、惯性矩I(I=Zt3/12)进行受力变形分析。根据Euler梁理论及载荷边界可知,横梁L发生弯曲变形,变形在梁的中央B点处达到最大,即是梁的挠度w(δ1);侧壁l的变形为悬臂梁的弯曲收缩变形(δ2和δ3)。因载荷作用线过结构的纵向对称轴,且结构横梁及侧壁的变形高度对称,故仅取1/4结构进行计算,如图2所示。

图2 1/4结构(a)和梁的变形(b)

(1)

式(1)中:上标u表示均布载荷(uniform load);δ1x为δ1在x方向的分量(δ1x=0);δ2x为δ2在x方向的分量,δ3x为δ3在x方向的分量;δ1y为δ1在y方向的分量;δ2y为δ2在y方向的分量,δ3y为δ3在y方向的分量。

横梁的等效受力可转化为简支梁受均布载荷作用的情况,其变形量δ1(挠度w)可由与梁长度x有关的弯矩方程[15]求出,挠曲线微分方程和弯矩方程等式如下:

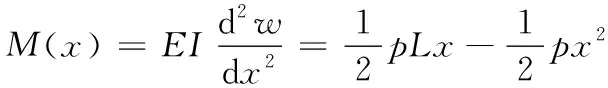
(2)

积分2次后可得挠度方程

(3)

式(3)中:C1和C2为积分常数,可由边界条件确定,即

(4)

从而横梁L的最大变形量δ1可表示为

(5)

侧壁l因受集中力F2=0.5pLsinθ和F3=0.5pLcosθ作用而发生弯曲变形[4],其变形量δ2和δ3分别为

(6)

(7)

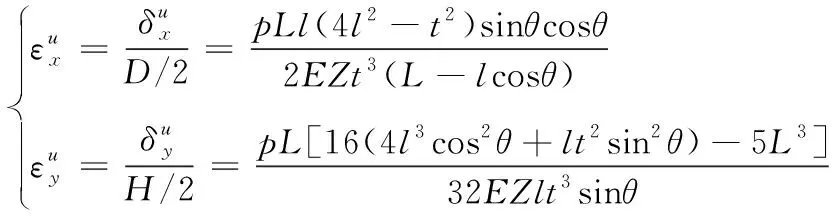
(8)

(9)

(10)

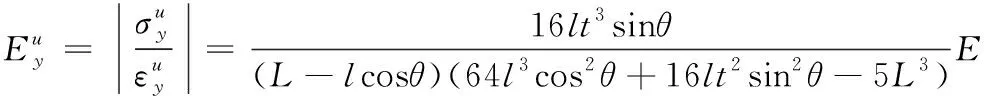
(11)

1.3 平板载荷边界

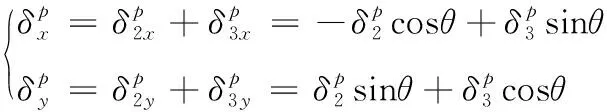
(12)

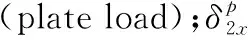
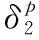
(13)

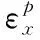
(14)

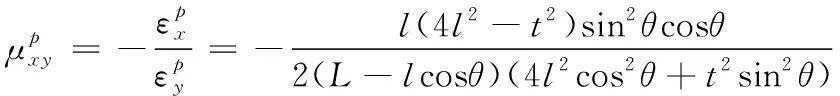
(15)

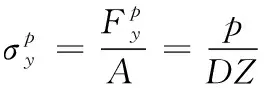
(16)

(17)

1.4 集中载荷边界

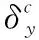
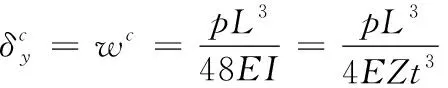
(18)

式(18)中:上标c表示集中载荷(concentrated load);wc为集中力作用下的挠度。

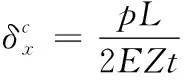
(19)

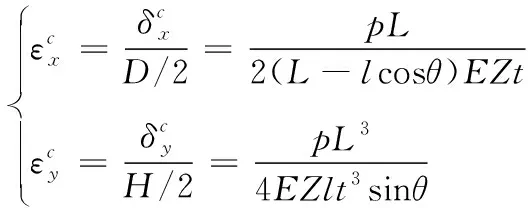
(20)

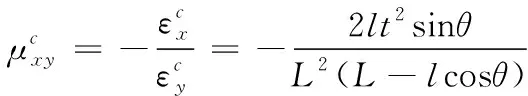
(21)

根据图1,集中载荷作用时,等效应力σ3沿横梁方向逐渐变化,并在载荷作用处达到最大。因此,结构横截面上的应力不相等,其任一纵截面的名义应力是一个沿宽度变化而变化的函数。根据横梁受载的边界条件,可构造如下的应力函数:

(22)

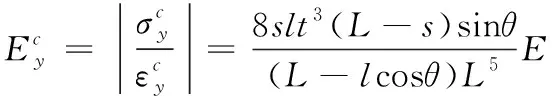
(23)

2 等效理论模型有限元验证

2.1 有限元模型

有限元分析中材料的本构模型采用不考虑温度效应的J-C本构,2024-T3铝合金的材料参数来自文献[1];密度2.78 g/cm3,弹性模量E=72.2 GPa,泊松比0.35。有限元模型的几何尺寸与1.1节保持一致,并采用C3D8R单元进行网格离散;通用接触摩擦系数设为0.1,网格尺寸0.5 mm,求解算法为Explicit/Dynamic。均布载荷边界条件通过在横梁L上施加压力(0.1 MPa)实现,平板载荷边界通过对横梁L施加纵向的位移实现,集中载荷边界通过在横梁L的中央施加集中力实现。

2.2 结果分析

内凹六边形负泊松比结构在3种边界载荷条件下的有限元分析结果如图3—图6。当边界为均布载荷时,如图3所示。结构横梁L因直接受载而率先发生变形,这是载荷类型及柔度差异导致的结果;横梁L变形类似于简支梁的弯曲,其最大变形量即为挠度;侧壁l因受均布载荷的分力作用而发生弯曲,类似于悬臂梁的弯曲。当边界为平板载荷时,如图4所示。横梁L因与平板接触而不发生变形,仅纵向上产生位移;侧壁l为唯一的承载部位,发生悬臂梁型弯曲变形,形成一个斜S构型。

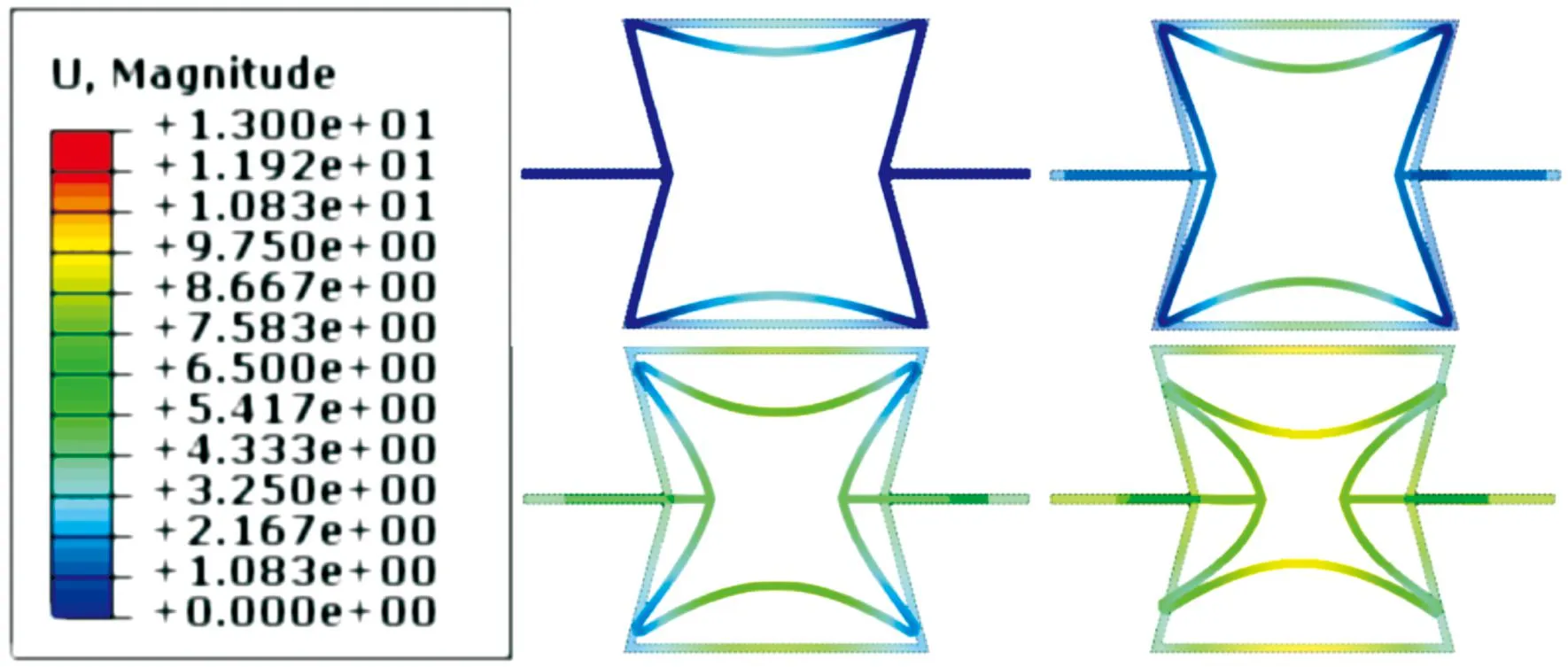
图3 内凹六边形结构压缩变形:均布载荷

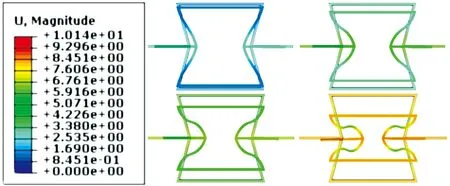
图4 内凹六边形结构压缩变形:平板载荷

图5 内凹六边形结构压缩变形:集中载荷

当边界为集中载荷时,如图5所示。与均布载荷相似,横梁L先发生简支梁型弯曲变形,且在加载位置处达到最大;侧壁l受横梁L弯曲收缩的作用而向内运动,基本不发生变形。内凹六边形结构压缩加载等效泊松比如图6所示。3种载荷边界条件下内凹六边形结构都实现了压缩-收缩的负泊松比效应,其原理为横梁L受压后通过力传递引起侧壁l向内的弯曲变形;然而,3种载荷边界引起的负泊松比值不同,甚至有的出现了正泊松比现象。

图6 内凹六边形结构压缩加载等效泊松比

对比可知,平板载荷条件下内凹六边形结构的负泊松比效应最佳;集中载荷是均布载荷作用的特例,两者横梁L的变形类型相似,负泊松比曲线走势也相似,但因外载不同而使得横梁L和侧壁l变形量的不同,均布载荷因侧壁l也发生变形而具有更好的负泊松比效应。值得注意的是,均布载荷和集中载荷作用下,结构进入塑性大变形阶段后内凹角处出现应力集中,是结构失效的初始位置;平板载荷作用时应力集中则出现在斜S构型的中心。

3 结论

本文针对3种载荷边界条件下内凹六边形结构的变形模式进行了分析,基于Euler梁理论建立了相应的等效弹性力学模型,并通过有限元分析对理论解进行了验证,主要研究结论如下:

1) 不同载荷边界条件下结构的变形模式不同,综合简支梁弯曲变形和悬臂梁弯曲变形获取了均布载荷作用下内凹六边形结构的等效力学模型,获取了结构在平板载荷作用下悬臂梁弯曲变形主导和集中载荷作用下简支梁弯曲变形主导的等效力学模型。

2) 有限元分析结果指出,达到一定的压缩应变后,3种载荷边界作用下内凹六边形结构都能实现压缩-收缩的负泊松比效应,其原理为横梁受压引起侧壁的向内运动;平板加载时结构的负泊松比效应最佳;均布载荷和集中载荷加载时,结构在压缩初期存在正泊松比现象,且内凹角处出现应力集中。

3) 均布载荷作用时,内凹六边形结构的横梁因载荷类型及柔度差异先发生弯曲变形,侧壁受均布载荷分力作用进而发生弯曲变形;平板载荷作用时,横梁因与平板接触而不发生变形,仅侧壁发生弯曲变形,并形成一个斜S构型;集中载荷作用时,横梁先发生弯曲变形,而侧壁基本不发生变形。

4) 等效泊松比预测值与有限元分析结果具有较好的吻合度;在弹性范围内,均布载荷条件下结构的等效泊松比为正,平板载荷条件能产生最大的等效负泊松比,集中载荷条件下等效泊松比接近于零;均布载荷和集中载荷对应的弹性阶段较小,负泊松比曲线都有先正后负的变化特征。