飞机双角拉伸接头的刚度可靠性灵敏度分析

许 新,苏长青,2,金嘉靖,杜兴盛

(1.沈阳航空航天大学 安全工程学院, 沈阳 110136;2.沈阳航空航天大学 辽宁省飞机火爆防控及可靠性适航技术重点实验室, 沈阳 110136;3.中国航发沈阳黎明航空发动机有限责任公司, 沈阳 110043)

0 引言

飞机的连接结构实现了不同构件间的连接和载荷的传递与分配,在使用过程中,连接接头处容易产生应力集中。正确分析接头的整体受力特性及应力分布特征是减小应力集中的关键[1]。双角接头是飞机支撑结构中常用的拉伸接头,与单角拉伸接头的L形设计相比,双角接头的T[2]设计对中央壁板的要求更高,常用来作为带耳片可拆卸接头的支撑。有限元分析方法在研究双角接头时是一个重要的手段,其计算结果较为准确,可以用来解决实际工程中复杂的问题。

文献[3]基于有限元法,研究了使复合材料多螺栓连接接头均匀承载的策略。文献[4]采用有限元方法对多钉结构的金属连接件的载荷分配进行了研究。文献[5]分析了机翼接头强度及工况并加以改进。文献[6]采用MSC.Patran 软件找出某机型货舱门下部连接接头的最大应力点并确定危险位置。文献[7]采用有限元法对碳纤维复合材料层合板之间铆胶连接进行了静力拉伸试验。文献[8]通过 ANSYS 有限元分析软件计算和试验来研究铆钉钉杆尺寸与铆接结构件间干涉量的关系。

文中利用APDL命令流进行编程建模,以双角拉伸接头为研究对象,考虑了倒角半径、端部厚度、中央壁板厚度、底板厚度等参数对双角接头刚度的影响规律。通过改变随机参数的尺寸,采用有限元仿真分析获得了对连接结构刚度影响较大的参数,根据刚度破坏理论建立极限状态方程,应用拉丁超立方抽样法得到双角接头在6种可靠度情况下的可靠性灵敏度,为结构优化及尺寸优化提供了方向。

1 双角拉伸接头有限元分析

在ANSYS经典界面中对双角拉伸接头进行自底向上的几何建模。双角接头的结构由2块梯形底板、中央倾斜壁板及双螺栓孔端部组成[9],其结构如图1所示。该模型采用SOLID187实体单元,材料为铝合金7050, 弹性模量为71 GPa,泊松比为0.31。

该模型划分网格后共有224 911个实体单元,354 785个节点,在对接头进行刚度分析时,需要在壁板紧固件孔处施加全约束,在端部螺栓处分别施加30 kN的水平拉力,使得模拟结果更加符合实际情况,其位移情况由位移云图2所示。

图1 双角拉伸接头结构示意图

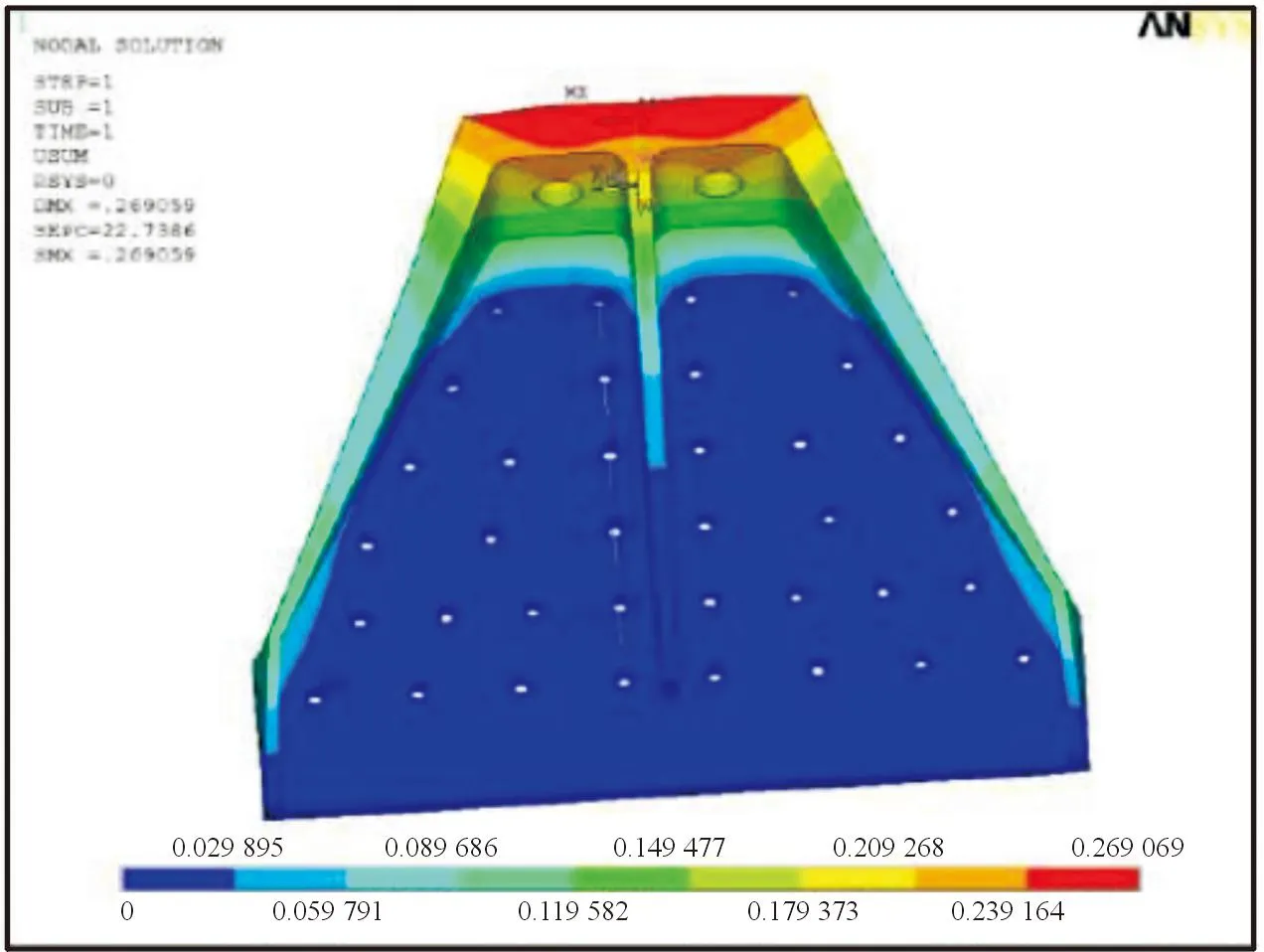
图2 端部螺栓孔周施加30 kN水平拉力的位移云图Fig.2 Displacement nebulae of 30 kN horizontal tension applied around hole of end bolt

通过计算得出最大位移点的坐标为(33.635 9,-14.714 2,71.456 3),最大位移为2.691×10-4m。将上述工况中最大位移作为参考依据,通过改变双角拉伸接头尺寸参数1/4的值,根据5种参数对其刚度的影响,找到对刚度影响最大的参数。分析的工况为以下10种,并将结果记录在表1中。

工况1～10分别为:将紧固件孔半径增加1 mm;将紧固件孔半径减小1 mm;将倒角半径增加2.5 mm;将倒角半径减小2.5 mm;将端部厚度增加6 mm;将端部厚度减小6 mm;将中央壁板前后端厚度增加1.5或1 mm;将中央壁板前后端厚度减小1.5或1 mm;将底板厚度增加2 mm;将底板厚度减小2 mm,各工况位移如图3所示。

图3 工况1—10的位移云图

表1 10种工况的最大位移

通过对以上工况进行分析得出:双角接头的最大位移量都随着5个参数的增加而减小,对于双角接头的刚度影响最大的是底板厚度,其次影响较大的为中央壁板厚度、端部厚度,而紧固件孔半径和倒角半径对于双角接头的刚度影响最小。

2 双角拉伸接头可靠度与灵敏度分析

2.1 双角拉伸接头可靠度计算

双角拉伸接头的刚度破坏旨在外力作用下最大位移值超过允许值[10],若最大位移值小于允许值则结构能够可靠工作,反之结构失效。公式表示如下:

结果显示，各景点通达性系数逐步上升，尤其是2008年之后，无论是单个景区还是南充市景区整体的交通网络可达性均显著提高。这与大力发展旅游产业紧密相关，尤其是在经历过2008年汶川大地震之后，不断加大道路建设投资力度，有力地推动了南充市旅游产业的发展。

r(X)>r允许

(1)

根据刚度破坏理论,定义双角接头的刚度可靠性极限状态方程如下:

Z(X)=r允许-r(X)=0

(2)

r(X)=D(R1,R2,RD,EX1)

(3)

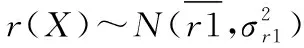
(4)

失效概率计算过程为

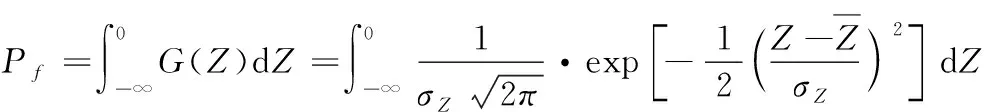
(5)

将正态分布变量Z转化为标准正态分布,则失效概率可写为

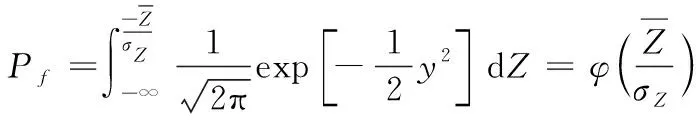
(6)

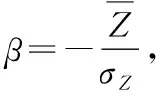
Pf=φ(-β)

(7)

其中,β为可靠性指标,则可靠度计算公式为

R=1-Pf=1-φ(-β)=φ(β)

(8)

2.2 双角拉伸接头可靠性灵敏度计算

双角接头的灵敏度为失效概率对Pf随机参数xi的分布参数μxi、σxi的偏导数[12-13]:

(9)

(10)

采用样本均值来代替总体均值以及标准差,则均值、标准差灵敏度为

(11)

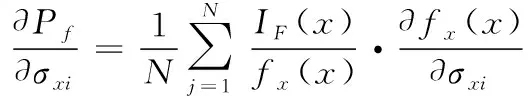
(12)

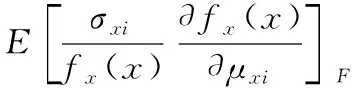
(13)

其估计值为

(14)

对于正态变量有

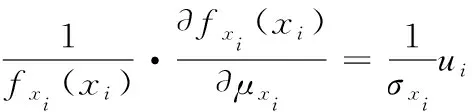
(15)

式(15)中:ui为基本随机向量x=(x1,x2,…,xn)T中的第i个分量xi引入的标准正态量。除去量纲影响的均值、标准差失效灵敏度分别为

(16)

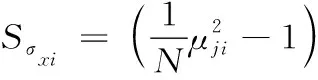
(17)

式(17)中:uji为j个样本xj=(xj1,xj2,…,xjn)的第i个分量xji的标准正态样本。

3 数值算例

通过有限元分析的位移云图可以看出端部螺栓孔周变形较大,因此选择端部螺栓孔半径(R2)、紧固件孔半径(R1)及倒角半径(RD)、双角接头的弹性模量(EX1)、施加力的大小、位移允许量r允许为分析的随机变量。随机变量分布类型如表2所示。

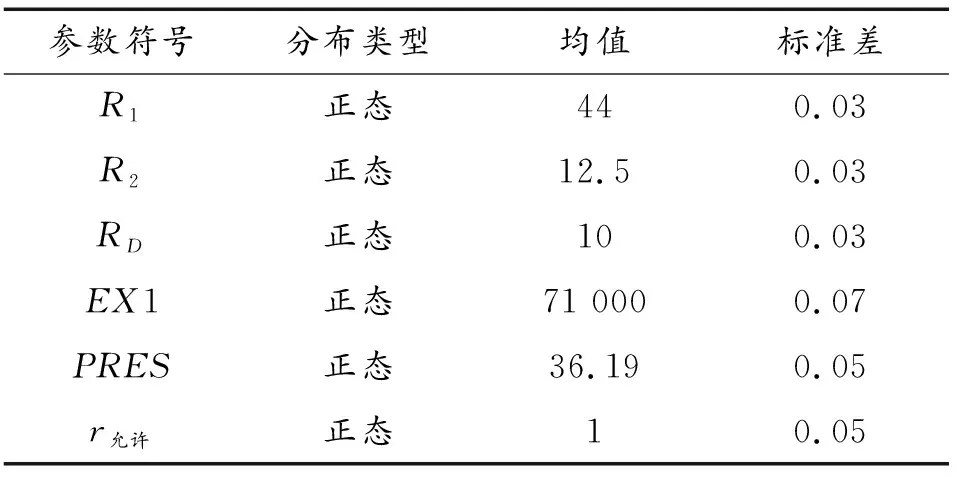
表2 双角拉伸接头随机参数统计特性

双角拉伸接头选用拉丁超立方法进行随机抽样,为了使抽样结果达到较高精度要求,本次取抽样次数为1 000次进行循环仿真[16]。得出不同的双角接头最大位移下接头的可靠度,详细结果如表3所示。

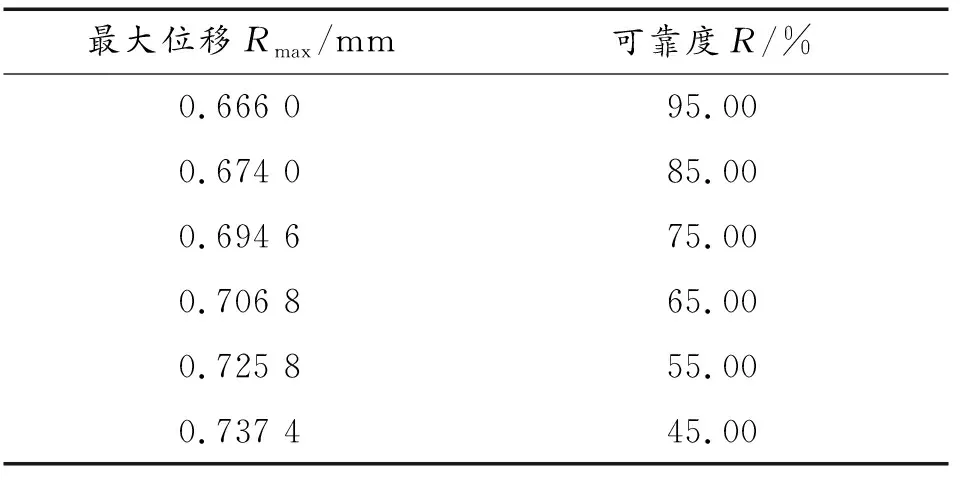
表3 双角拉伸接头可靠度

双角接头在不同可靠度条件下的各项随机参数可靠性灵敏度[17]如图4—图9所示。

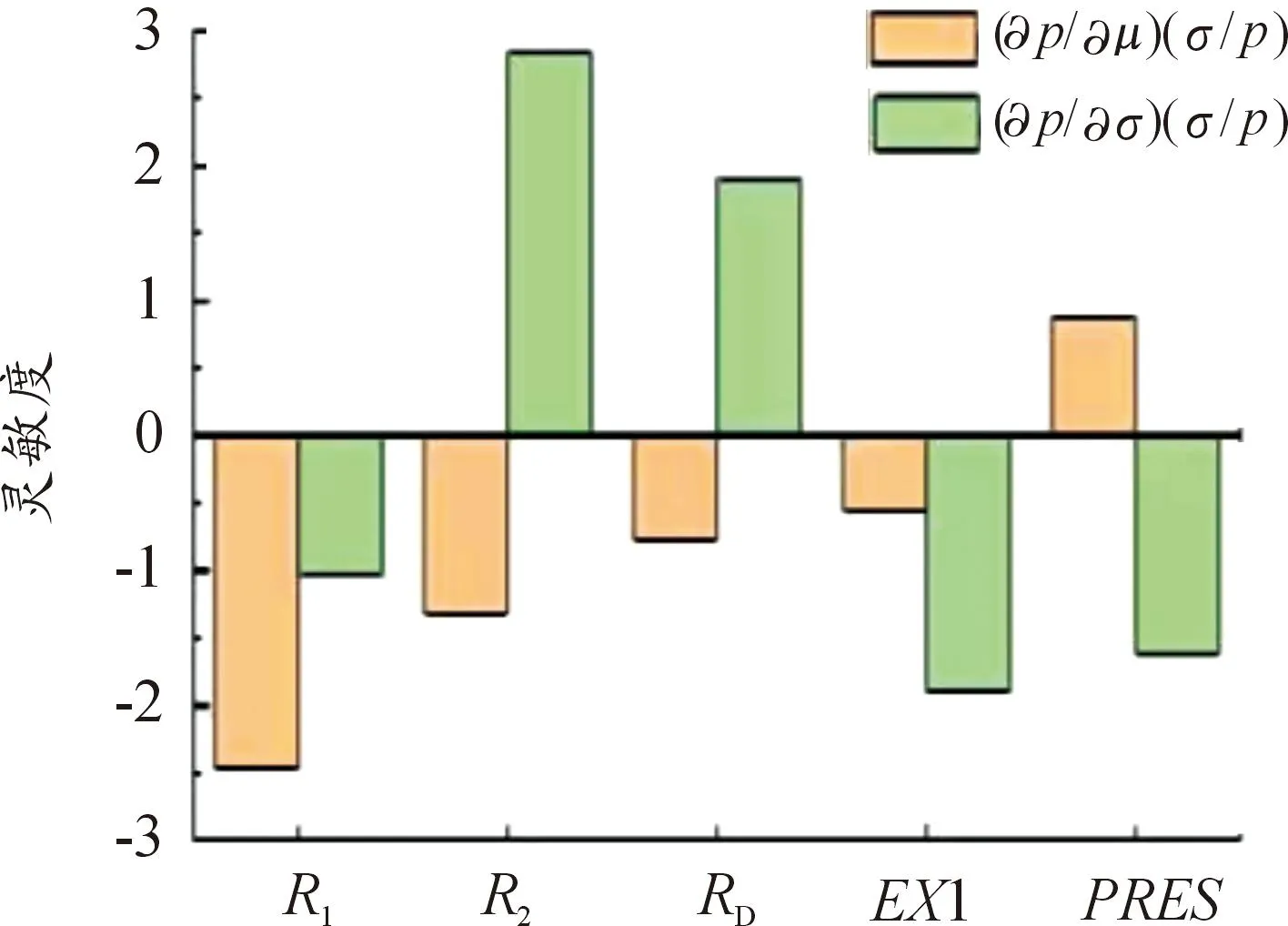
图4 R=95.00%时各参数灵敏度

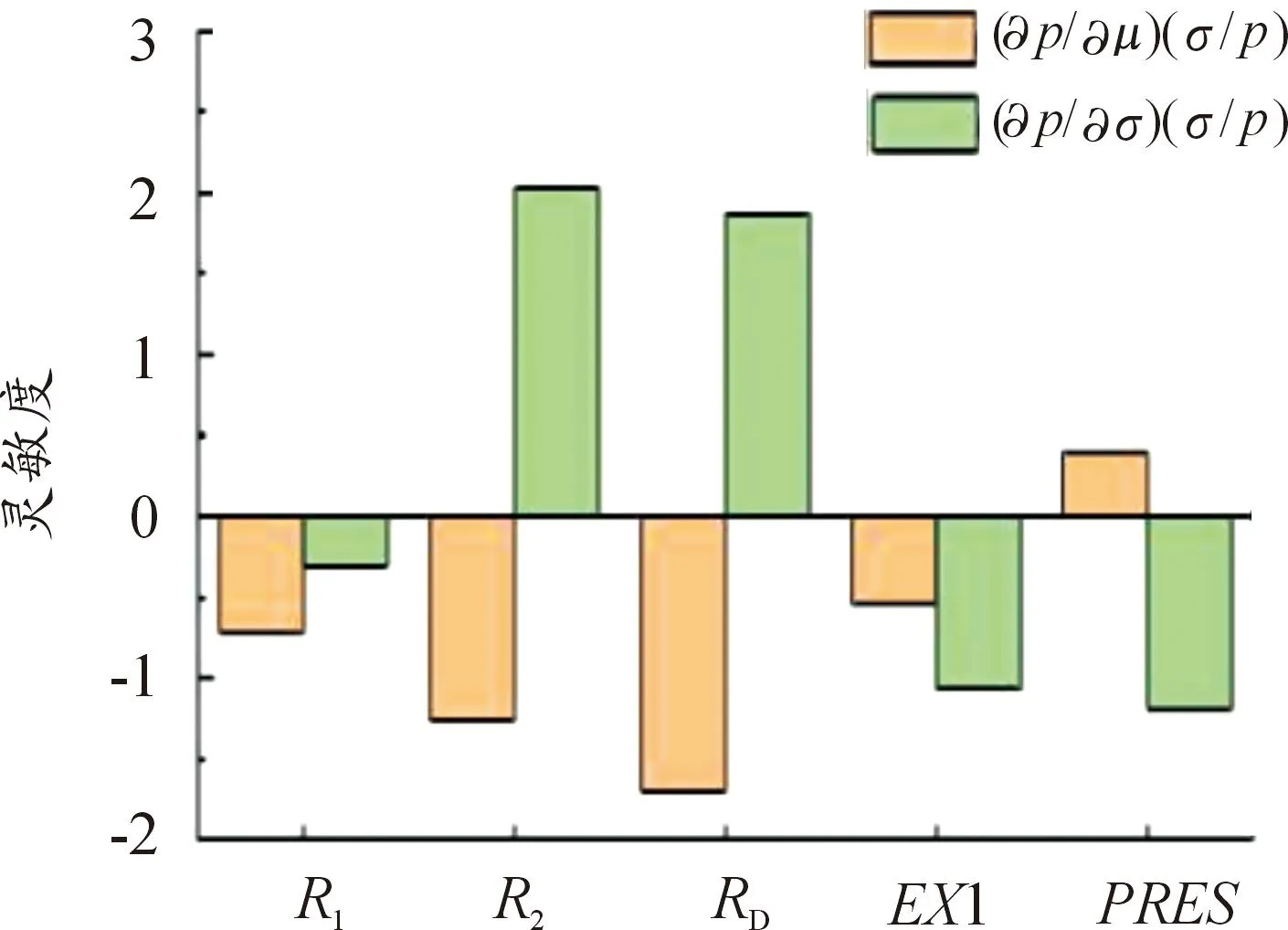
图5 R=85.00%时各参数灵敏度

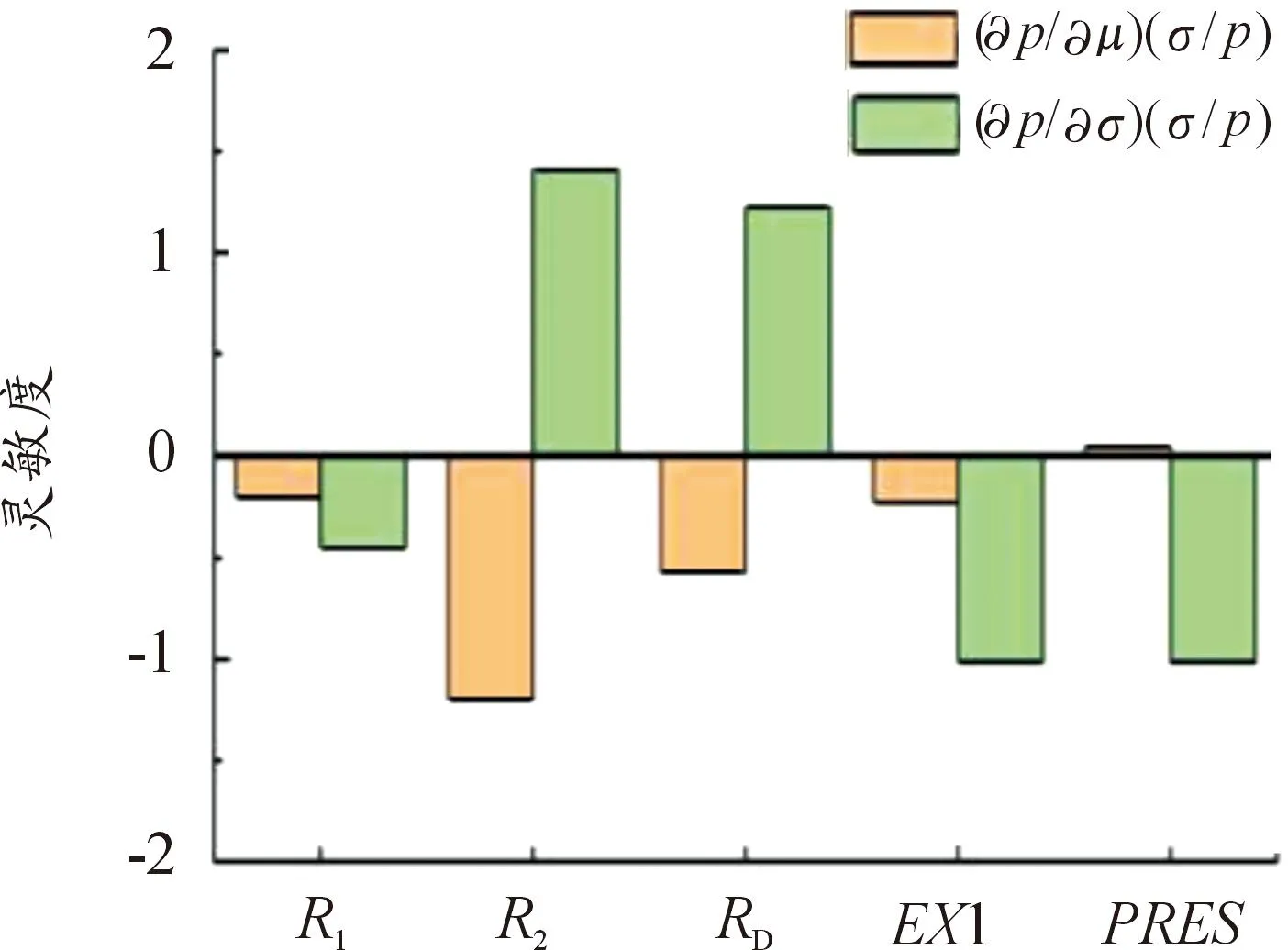
图6 R=75.00%时各参数灵敏度

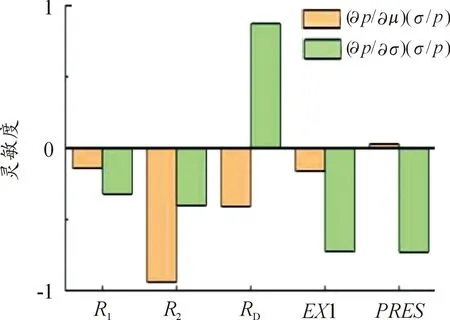
图7 R=65.00%时各参数灵敏度

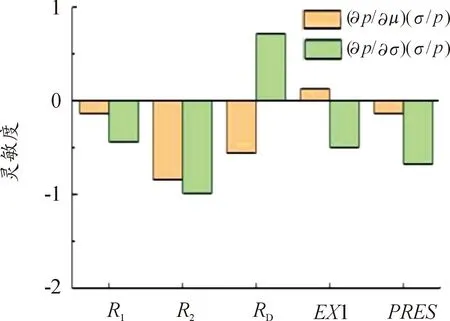
图8 R=55.00%时各参数灵敏度

图9 R=45.00%时各参数灵敏度

通过以上分析可得:针对双角接头各随机参数的均值可靠性灵敏度而言,可靠度为65.00%、75.00%、85.00%、95.00%时,双角接头参数PRES的均值可靠性灵敏度为正值;可靠度为55.00%、45.00%时EX1的均值可靠性灵敏度为正值,说明这些参数均值的增加降低了接头的可靠度,影响是积极的,随着参数均值的增加导致接头可靠度的降低。因此,在设计和制造中应当控制好该尺寸参数的均值;同理可得随机参数R1、R2、RD的均值可靠性灵敏度为负值,说明这些参数均值的增加会大幅提高双角接头的可靠度。对双角接头的可靠度影响是消极的,随着这些参数的均值增加,双角接头的可靠性就会降低。可靠性灵敏度绝对值最大的随机参数为R2,说明此参数的均值对双角接头的可靠度影响要大于其他参数的均值对接头的影响,在设计制造中要优先考虑R2均值的积极影响。

针对双角接头各随机参数的标准差可靠性灵敏度而言,当可靠度小于85.00%时,随机参数R2、RD的标准差可靠性灵敏度为正值,说明这2个随机参数的标准差对双角拉伸接头失效概率产生积极影响;当可靠度为85.00%、75.00%、65.00%、55.00%时,参数R1、EX1、PRES的标准差可靠性灵敏度均为负,说明这些参数的标准差对双角拉伸接头的失效概率产生了消极影响。随着这几种参数均值的增加,会有效降低系统的失效率,进而提高系统可靠度。

4 结论

通过对飞机双角拉伸接头结构进行静力学分析,改变接头的尺寸参数,根据刚度破坏理论判定均未失效。采用蒙特卡罗法的改进方法——拉丁超立方抽样法进行随机抽样,得到各个随机参数对系统的可靠性灵敏度,灵敏度绝对值表示随机参数对系统可靠度影响的剧烈程度[18]。灵敏度为正值,表明随着这一随机参数的增加,双角拉伸接头的可靠度也会增大;灵敏度为负值,表明随着这一随机参数的增加,双角拉伸接头的可靠度会减小。绝对值越大表明随机参数对系统可靠度影响越大,反之则越小。

从灵敏度结果中获得了对可靠性影响程度较大的敏感参数和对可靠性影响程度较小的不敏感参数:R2的均值灵敏度及EX1、PRES的标准差的可靠性灵敏度为负且最大;PRES的均值灵敏度及RD标准差灵敏度为正且最大;R1的灵敏度值均较小,因此R1为不敏感参数。在实际工程中将该不敏感参数作为确定性变量,以减少变量维数,提高计算效率。