嵌入式共固化缝合阻尼复合材料面内弹性参数

刘昭阳,梁 森,孙瑞骏,罗 皓,胡子健,朱 笛

(青岛理工大学 机械与汽车工程学院, 山东 青岛 266520)

0 引言

嵌入式共固化缝合阻尼复合材料(ECSDC)是由多种的不同性质的材料以共固化工艺通过物理或化学的方法形成的多相固体。复合材料板中的基体相、面内增强相和粘弹性阻尼材料在性能上相互协调,从而得到单一材料所不能企及的良好的阻尼性能和综合力学性能。纤维缝线对上、下树脂增强纤维蒙皮夹钳阻尼结构进行缝合,在共固化工艺时,蒙皮中的树脂会沿缝合线流动贯穿整个复合材料层间结构形成复合钉。该特殊结构作为z方向的增强相能够有效地增强复合材料的力学性能和层间剪切性能,使新结构具有三向力学可设计性的优点,利于该结构在精密仪器制造、航空航天等领域的推广。

在研究胞元材料的面内等效弹性参数方面,文献[1-3]中用理论近似法建立了胞元结构面内等效弹性参数的理论分析模型。Dos Reis和Ganghoffer[4]、Arabnejad与Pasini[5]采用渐近均质法(asymptotic homogenization,AH)获得了周期性胞元结构的面内等效弹性参数。Lainé等采用代表体积单元法(representative volume element method,RVE)分析了胞元夹芯结构的横向剪切刚度[6]。文献[7-10]中给出了圆柱状蜂窝胞元、六边形胞元、梯形胞元、方形胞元的等效弹性模量解析方程,并采用有限元方法(finite element method,FEM)验证了理论模型的有效性。文献[11-14]中研究了点阵结构的面内等效弹性参数。

在研究阻尼薄膜夹嵌复合材料性能方面,潘利剑等[15]使用结合的模态应变能法和模态叠加法,分析了连续阻尼薄膜夹嵌复合材料的阻尼性能。Arikoglu与Ozkol等[16]将一阶剪切变形理论(first-order shear deformation theory,FSDT)与广义微分求积法相结合,对阻尼薄膜夹嵌复合材料板进行了动力学分析。路庆贺等[17]使用FSDT和Hamilton原理,推导了阻尼夹芯复合材料加筋板的应变能、动能公式,并使用变分原理建立了该结构的控制微分方程。王绍清等[18-19]根据Rayleigh-Ritz法计算了单层与多层阻尼薄膜夹嵌复合材料带筋结构的损耗因子和模态频率,并对结构进行了优化设计。闫盛宇等[20]开发了ECSDC板的制作工艺,为测试该结构的抗拉伸性能、层间剪切性能和阻尼性能,搭建了例如层间剪切试验、拉伸破坏试验、自由衰减试验等的试验平台,为ECSDC以后更深入的研究奠定了基础。

目前国内外鲜有文献对缝合纤维阻尼复合材料胞元结构的面内等效弹性参数的问题进行研究,这将阻碍对ECSDC结构的继续研究与应用推广。为此本文中通过建立ECSDC中复合钉贯通的面内纤维折线变形模型,探索该结构的面内等效弹性参数问题。由于复合钉贯通整个层合结构,上、下蒙皮的弹性参数未知,因此从复合钉贯通的纤维增强阻尼薄膜的面内等效弹性参数计算入手,过渡到ECSDC。使用ANSYS和Matlab研究ECSDC典型结构,将理论预测数据与模拟预测数据和文献值相比较,验证该理论模型的准确性,为ECSDC结构的动力学研究及使用推广提供理论依据。

1 缝合阻尼复合材料的面内等效弹性参数

由于复合钉贯通了缝合阻尼复合材料的整个层合结构,且上、下蒙皮的弹性参数未知。因此,先从缝合纤维增强阻尼薄膜的面内等效弹性参数计算入手,过渡到ECSDC。

1.1 基本假设

采用改进锁式缝合方式[21]的ECSDC结构如图1所示,建立的x-y-z宏观结构笛卡尔坐标系如图2所示。

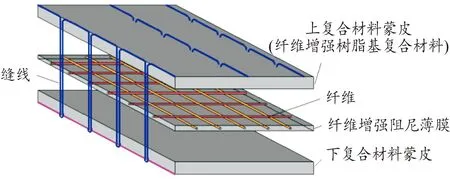
图1 采用改进的锁式缝合方式的ECSDC示意图

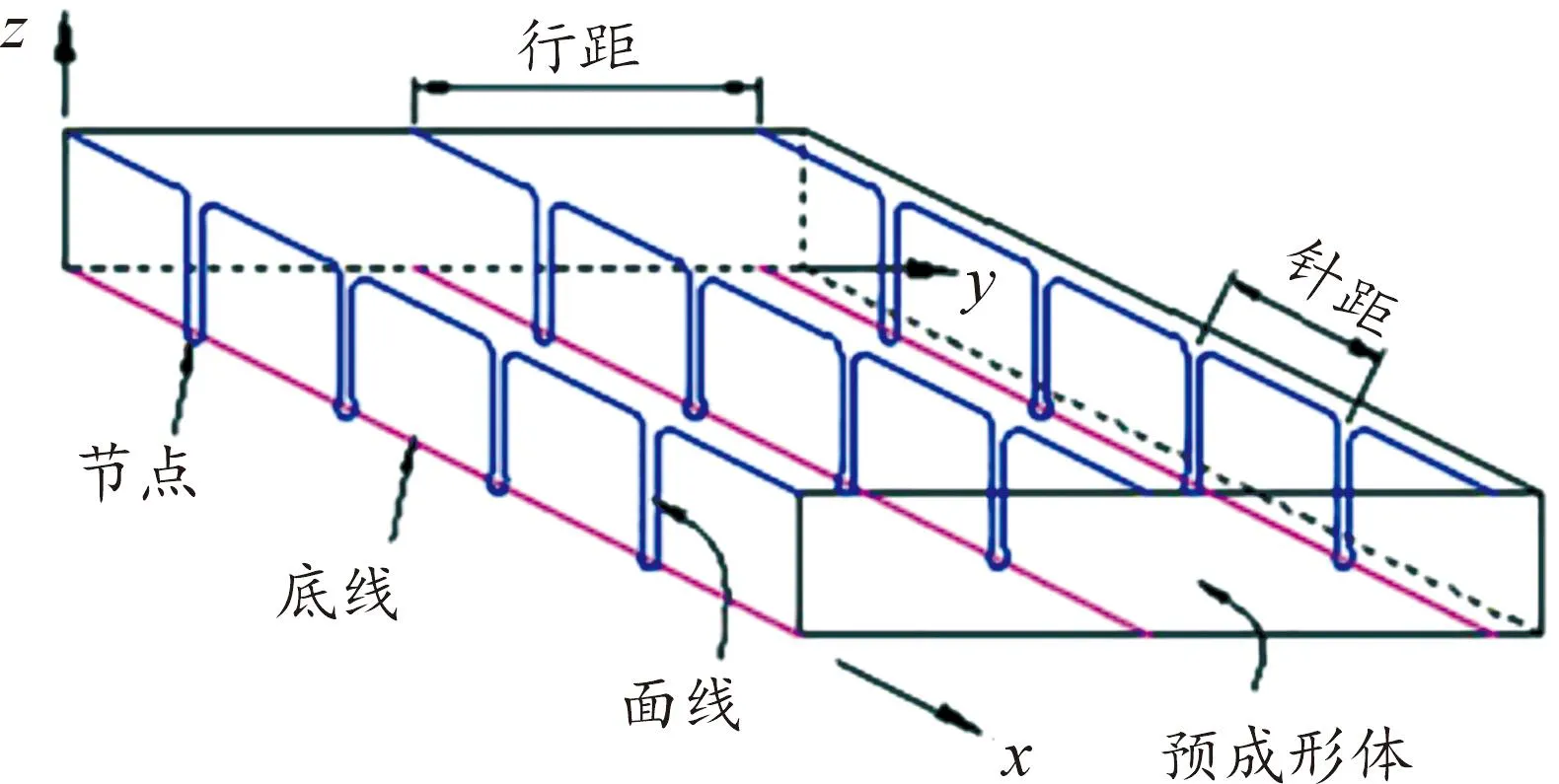
图2 笛卡尔坐标系示意图

为方便建模,假设如下:

1) 忽略纤维在针孔附近的局部损伤;

2) 底线与面线均不会发生卷曲,在缝合与固化工艺之后仍然保持圆形截面;

3) 在缝合之前,经纱与纬纱均为直线,缝合后仍然是直线;

4) 经纱变形区的纬纱不发生变形,纬纱变形区的经纱不发生变形;

5) 忽略缝合后纤维之间的拉伸-弯曲以及拉伸-剪切耦合影响。

若将缝合纤维阻尼薄膜视为周期性结构且每个周期内的纤维变形不发生改变,那么可以选取一个胞元结构建立复合钉贯通的面内纤维折线变形模型(如图3所示)。其中行距(L)定义为2行缝线之间的距离,针距(N)定义为同一行缝线上2个相邻针孔的中心距;η1-η2-η3为胞元结构的局部坐标系。因为胞元结构的对称性,为简化模型选取1/4的胞元(如图4所示)进行研究。

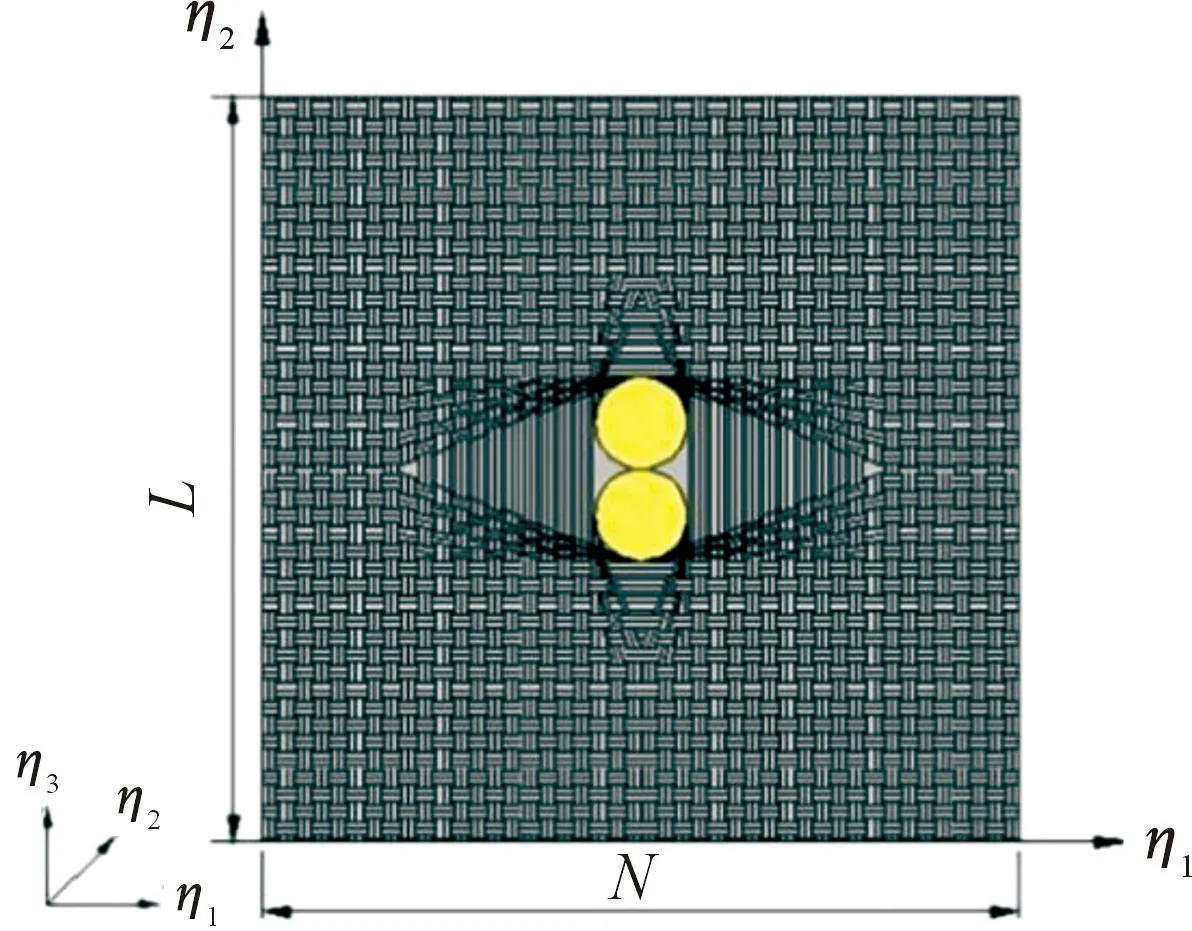
图3 复合钉贯通的面内纤维折线变形模型

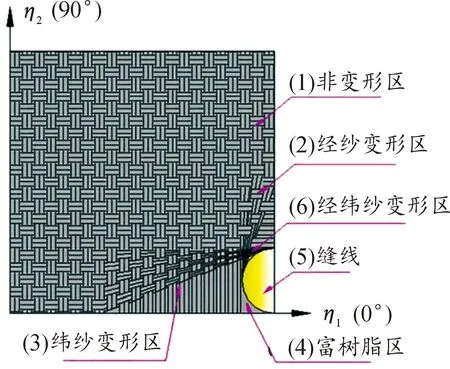
图4 1/4胞元结构

因为复合钉的插入导致纤维增强阻尼薄膜的面内力学性能分布不均,接下来将分析每个区域(已在图4中标号划定)的弹性参数。

1.2 非变形区的面内等效弹性参数

缝合纤维增强阻尼薄膜非变形区的主要成分是纤维和阻尼材料,材料坐标系如图5所示。

图5 平纹编织纤维的坐标轴

根据文献[22]可得到经纱单向板和纬纱单向板的弹性参数:

Em={E1,m,E2,m,G12,m,ν21,m,ν12,m}

(1)

式(1)中:m为单向板,当m=j、w时分别表示经纱单向板、纬纱单向板;E1,m、E2,m分别为单向板在材料1轴、2轴的弹性模量,GPa;G12,m为单向板在1-2平面内的剪切模量,GPa;ν21,m、ν12,m为单向板的泊松比。

平纹编织阻尼基复合材料的弹性参数表达式为:

(2)

式(2)中:E1和E2分别为材料坐标系1轴、2轴的弹性模量,GPa;G12为1-2平面内的剪切模量,GPa;和是泊松比;ν12和ν21分别为平纹编织单层板中纬纱和经纱的相对含量。

对于变形区而言,复合钉周围的纤维会发生一定程度的偏转。缝合纤维增强阻尼薄膜的铺层角度θ对纤维偏转的影响可近似认为是0°铺层下纤维偏转之后再旋转角度θ。

在非变形区,材料主轴与局部坐标轴平行,即:夹角θ(1)=0。该区域的弹性参数根据式(1)—式(2)获得:

(3)

式(3)中,上标(1)表示非变形区的区域编号。

1.3 经纱变形区的面内等效弹性参数

应力-应变关系为(应力单位:GPa):

(4)

其中:

(5)

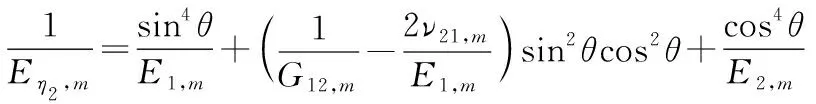
(6)

(7)

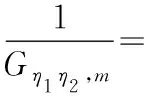
(8)

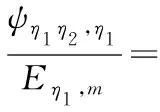
(9)

(10)

如图6、图7所示,经纱纤维的偏转变形程度随位置和缝合方向的变化而变化。

图6 缝合方向平行于x轴的折线变形模型

图7 缝合方向平行于y轴的折线变形模型

当缝合方向平行于x轴时,经纱纤维与η1轴的夹角θ(2)可表示为:

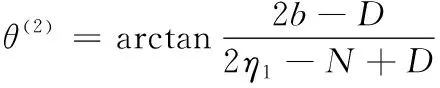
(11)

当缝合方向平行于y轴,θ(2)可表示为:

(12)

其中:b和a分别代表缝合方向平行于x轴和y轴时经纱变形区的长度。

将经纱偏转角θ(2)代入式(5)—式(10),可得到经纱微带dη1的弹性参数。

当缝合方向平行于x轴时,将式(11)代入式(5)—式(10),有:

(13)

(14)

(15)

(16)

(17)

由式(1)可得:

Ej={E1, j,E2, j,G12, j,ν21, j,ν12, j}

(18)

且该区域内经纱的平均弹性参数为:

(19)

式(19)中:上标m-warp表示经纱微带dη1,且有:

(20)

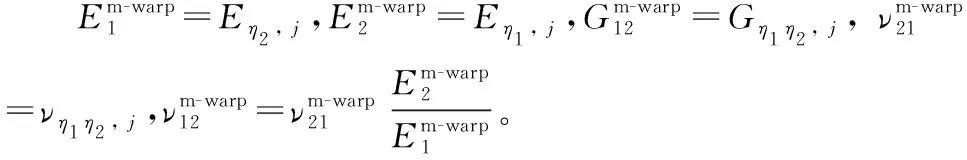
当缝合方向平行于y轴,将式(12)代入式(5)—式(10),有:

(21)

(22)

(23)

(24)

(25)

该区域经纱的平均弹性参数为:

(26)

由式(1)可得到在经纱变形区的纬纱弹性参数:

Ew={E1,w,E2,w,G12,w,ν21,w,ν12,w}

(27)

将经纱和纬纱的弹性参数代入式(2)得到经纱变形区的弹性参数:

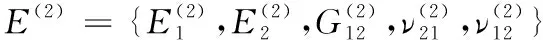
(28)

式(28)中:上标(2)表示经纱变形区的区域编号。

1.4 纬纱变形区的面内等效弹性参数

纬纱纤维变形段与η1轴之间的夹角θ(3)随坐标η2的增大而减小。

当缝合方向平行于x轴时,有:

(29)

当缝合方向平行于y轴时,有:

(30)

将经纱偏转角θ(3)代入式(5)—式(10),可得到纬纱微带dη2的弹性参数。

当缝合方向平行于x轴时,将式(29)代入式(5)—式(10),有:

(31)

(32)

式(31)—式(32)中:E1,w、E2,w、G12,w与v21,w可由式(1)获得。

该区域内纬纱的平均弹性参数为:

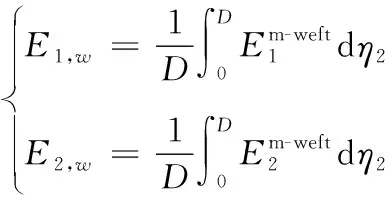
(33)

式(33)中:上标m-weft表示纬纱微带dη2,且有:

(34)

当缝合方向平行于y轴时,将式(30)代入式(5)—式(10),有:

(35)

(36)

该区域内纬纱的平均弹性参数为:

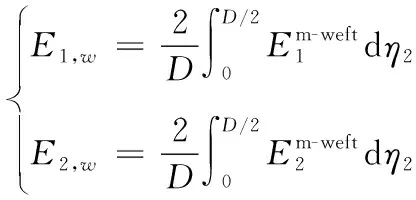
(37)

根据第4条假设,在该区域内经纱的弹性参数可由式(1)得到,有:

Ej={E1, j,E2, j,G12, j,ν21, j,ν12, j}

(38)

将经纱与纬纱的弹性参数代入式(2),获得纬纱变形区的弹性参数,有:

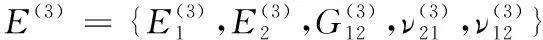
(39)

式(39)中:上标(3)代表纬纱变形区的区域编号。

1.5 富树脂区的面内等效弹性参数

富树脂区内主要是在复合材料共固化时填充了缝线与增强纤维之间空隙的树脂,因此可以看作各向同性材料,该区域的弹性参数:

(40)

其中:上标(4)代表富树脂区的区域编号,且:

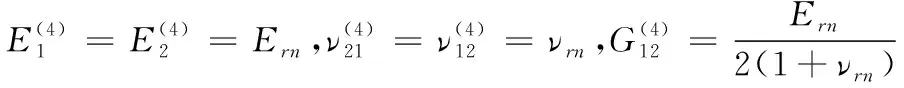
(41)

式(41)中:下标rn表示树脂。

1.6 缝线的面内等效弹性参数

缝线区需考虑缝线的横向强度,因此:

(42)

其中:上标(5)代表缝线区的区域编号,并且:

(43)

式(43)中:下标s表示缝线。

1.7 经纬纱变形区的面内等效弹性参数

在该区域内,经纱与纬纱均发生偏转。当缝合方向平行于x轴时,将式(18)与式(33)代入式(2);当缝合方向平行于y轴时,式(27)与式(37)代入式(2),有:

(44)

其中:上标(6)代表经纬纱变形区的区域编号。

1.8 缝合纤维增强阻尼薄膜的面内等效弹性参数

根据混合定理,获得胞元结构的面内等效弹性参数。由于胞元结构的平均属性可以描述宏观结构的有效属性,因此,缝合纤维增强阻尼薄膜的弹性参数为:

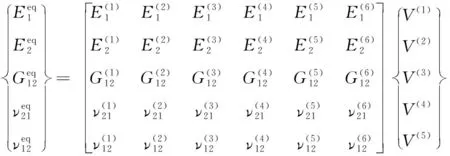
(45)

其中:上标eq表示面内等效弹性参数;是每个区域的相对体积分数,可得:

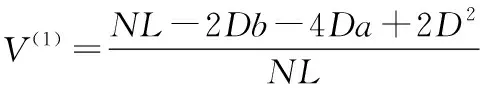
(46)

(47)

(48)

(49)

(50)

(51)

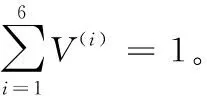
1.9 缝合阻尼复合材料的面内等效弹性参数

在ECSDC中,有复合钉贯通的上、下蒙皮的面内等效弹性参数可参照缝合纤维增强阻尼薄膜的数学模型,只需把模型中阻尼材料替换为树脂,由式(45)可得:

(52)

其中:Eeq(r)为第r层的等效弹性参数矩阵,r=1,2,3;r=1、3时为上、下蒙皮的弹性参数,r=2时为缝合纤维增强阻尼薄膜的弹性参数。

ECSDC第r层的应力-应变关系可写为:

ε(r)=S(r)σ(r)

(53)

其中:将第r层的铺层角度σ(r)和Eeq(r)矩阵中的元素代入式(11)—式(12),可获得第r层的柔度矩阵S(r)。

由文献[22]建立ECSDC的面内等效弹性参数模型。ECSDC的本构关系表达式为:

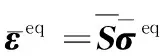
(54)

ECSDC中任一点的面内应力可通过均质化法[22]进行定义,即:

(55)

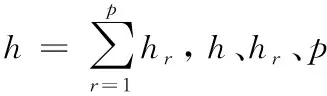
假设ECSDC的各层都经历了相同的面内应变,则:

(56)

将式(52)、式(53)、式(55)与式(56)代入式(54),缝合层合板的柔度矩阵可以借助每一层的柔度矩阵进行表示,即:

(57)

由式(57)即可获得ECSDC的面内等效弹性参数。

2 理论模型验证

为验证所推公式的准确性,首先将理论模型与ANSYS有限元软件模拟进行比较。选取长×宽为250 mm×25 mm且缝线间距为10 mm的ECSDC梁试件进行建模,试件总厚度为2.1 mm。在ANSYS软件中以SOLID185单元建立ECSDC模型,各复合材料层之间使用共节点进行连接。

上、下树脂增强蒙皮是玻纤/酚醛复合材料预浸料,上下层厚度为各1 mm,材料参数由文献[23]所得,如表1、表2所示;夹嵌的纤维增强阻尼薄膜是将平纹编织纤维布预浸阻尼溶液后压制而成,纤维布材料参数接近粘弹性材料,阻尼材料采用丁腈橡胶,该层厚度为0.1 mm,材料参数如表3、表4所示。缝线选取Kevlar-49,其材料参数由表5给出。

表1 玻纤/酚醛复合材料参数

表2 酚醛树脂材料参数

表3 平纹编织纤维布/丁腈橡胶材料参数

表4 丁腈橡胶粘弹性阻尼材料参数

表5 芳纶纤维参数

由于缝线相对其他结构要细的多,为方便芳纶纤维的建模,将其横截面简化为正方形,以纤维密度为1.44 g/cm3的1 500旦芳纶纤维为例,其纤维横截面积为0.12 mm2,故其简化后的正方形边长为0.346 4 mm。建模后的ECSDC梁试件如图8所示。

图8 建立的ECSDC梁试件模型

分别对缝合针距为8、10、12 mm的ECSDC梁试件的弹性参数进行ANSYS数值模拟计算,其中针距10 mm的ECSDC梁试件应力、应变如图9、图10所示。将理论模型在Matlab软件环境中编程,计算相同缝合针距的理论结果。结合文献[24]中试验所得相同缝合针距的弹性参数,将3种方式得到沿x轴方向的等效弹性模量E1在表6中列出,分别计算理论值与其他2种结果的相对误差并取绝对值。通过比较可以看出,3种方法得到的计算结果较为相近,相对误差均在5%以内,可以认为该理论模型是较为准确的。

图9 ECSDC梁试件的应力云图

图10 ECSDC梁试件的应变云图

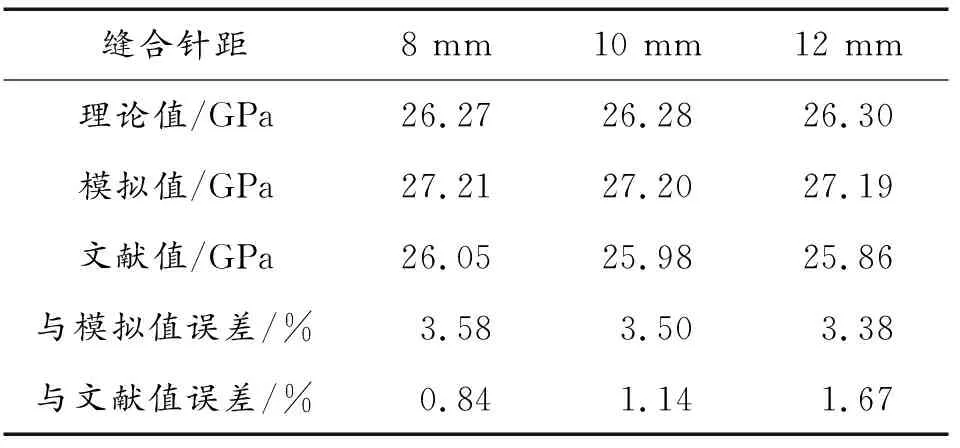
表6 理论计算与数值模拟、文献实验的结果比较

出现误差的主要原因:一是理论模型在计算时仅考虑了富树脂区和面内纤维偏转等因素,而文献中的试验还会受到如纤维损伤等因素影响;二是在有限元建模时对缝线进行了模型简化处理,且有限元模拟时不会考虑上述因素的作用。

3 设计参数对结构等效弹性参数的影响

基于已经验证的理论模型,进一步探讨缝合密度、缝线直径、铺层角度及缝合方向等设计参数的变化对ECSDC整体结构面内等效弹性参数的影响,揭示缝合工艺对结构各向异性的影响。

3.1 缝合密度的影响

由缝合密度的定义可知:缝合密度=1/(针距×行距)。通过改变针距和行距,研究缝合密度对结构面内等效弹性参数的影响。

保持模型的结构总尺寸、缝线行距、缝线直径及铺层角度等因素不变,研究缝合针距对结构面内等效弹性参数的影响。引入变化率这一概念:变化率=(缝合结构的弹性参数—未缝合结构的弹性参数)/未缝合结构的弹性参数。其变化曲线如图11和图12所示。

由变化曲线图可知,相较于未缝合结构(变化率为0),ECSDC 的面内等效弹性参数有所降低。当缝合针距相对较小时,ECSDC 结构弹性模量和剪切模量的降低比较明显,而随着缝合针距的增大,弹性模量和剪切模量逐渐趋于未缝合结构的弹性参数。即当缝线行距不变时,结构的面内等效弹性参数随缝合针距的减小而降低;另外,当缝合方向平行于x轴时,弹性模量E1的变化率比E2的变化率小;当缝合方向沿着y轴时,弹性模量E2的变化率比E1的变化率小,这表明缝合工艺提高了结构的各向异性。

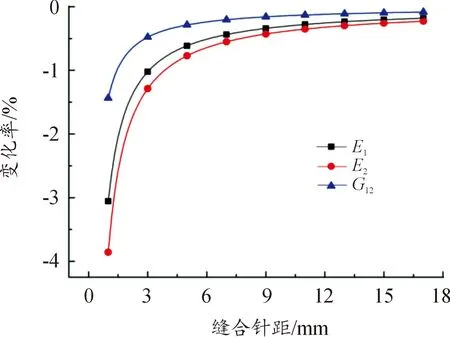
图11 面内等效弹性参数与缝合针距的变化关系 (缝合方向平行于x轴)

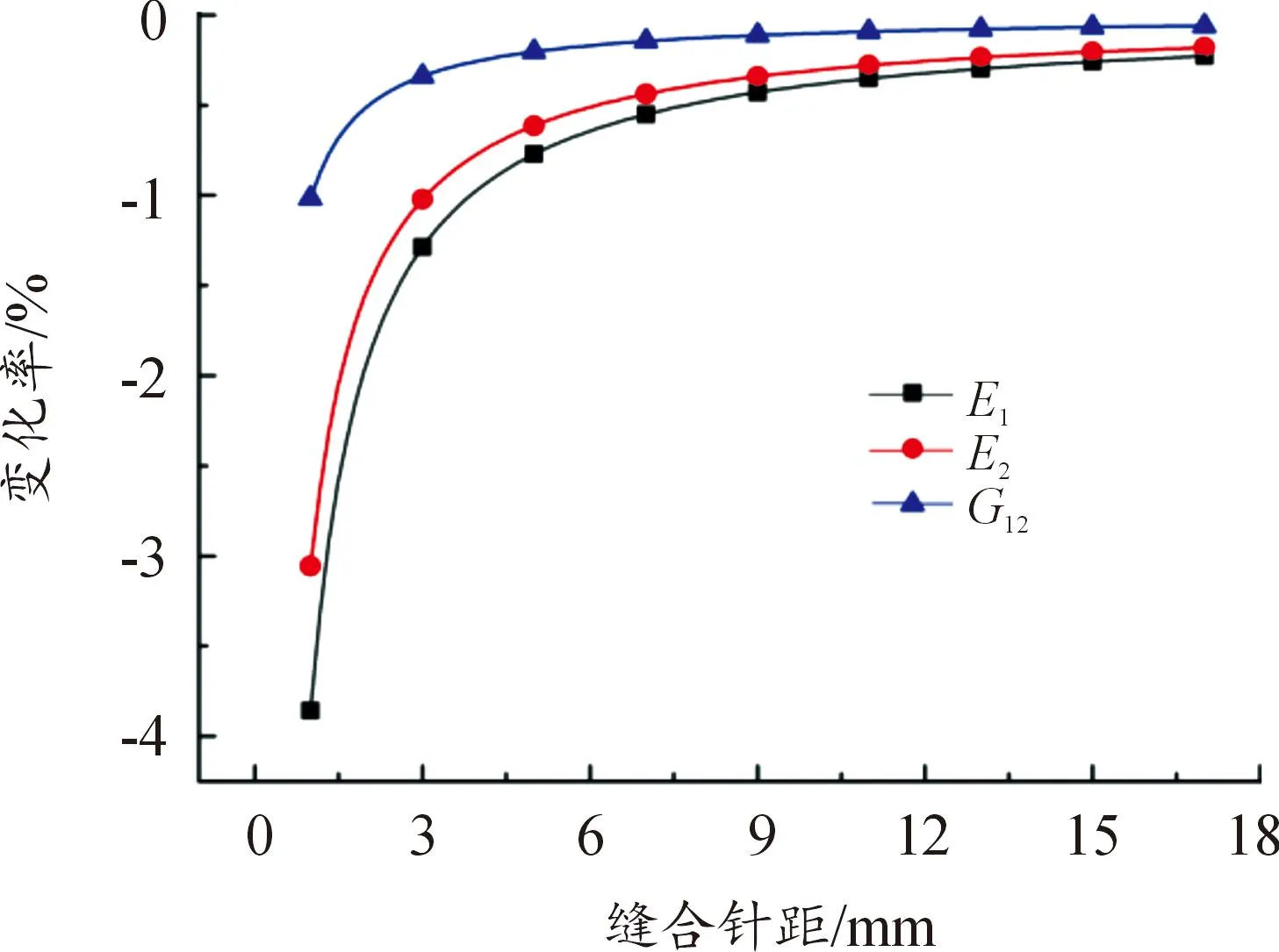
图12 面内等效弹性参数与缝合针距的变化关系 (缝合方向平行于y轴)

保持模型的结构总尺寸、缝合针距、缝线直径及铺层角度等因素不变,研究缝线行距对结构面内等效弹性参数的影响。得到的变化率曲线如图13和图14所示。

由变化曲线图可知:缝线行距对面内等效弹性参数的影响类似于缝合针距,即当缝合针距不变时,结构的面内等效弹性参数随缝合行距的减小而降低;另外,改变缝合方向后弹性模量E1和E2的变化率差异也表明了缝合工艺对结构各向异性的增强作用。

由缝合密度的定义,可以进一步得到以下结论:当缝线直径和铺层角度不变,ECSDC 结构的面内等效弹性参数会随缝合密度的增大而降低。原因包括2个方面:一是纤维弯曲会降低纤维的轴向力学性能,不同的缝合密度将导致纤维发生不同程度的偏转变形;二是富树脂区的布局差异会造成局部应力集中,从而降低结构的力学性能。缝合密度越大意味着富树脂区和发生偏转变形的纤维占比越大。

图13 面内等效弹性参数与缝线行距的变化关系 (缝合方向平行于x轴)

图14 面内等效弹性参数与缝线行距的变化关系 (缝合方向平行于y轴)

3.2 缝线直径的影响

保持模型的结构总尺寸、缝合针距、缝线行距和铺层角度等因素不变,且缝合方向始终平行于x轴,研究缝线直径对结构面内等效弹性参数的影响。得到的变化率曲线如图15所示。

由图15可知,当缝合针距与缝线行距不变,ECSDC 结构的弹性模量和剪切模量随缝线直径的增大而降低。主要原因是随着缝线直径的增大,面内纤维的偏转角增大,同时富树脂区的面积也增大,从而对结构面内等效弹性参数产生影响。

3.3 铺层角度的影响

保持模型的结构总尺寸、缝合针距、缝线行距和缝线直径等因素不变,且缝合方向始终平行于x轴,研究铺层角度对结构面内等效弹性参数的影响。结构的铺层顺序设计为[0/90//+90/0/90],其中变量表示纤维增强阻尼薄膜的铺层角度,即保持上、下蒙皮铺层角度不变,改变阻尼薄膜的铺层角度,得到的变化率曲线如图16所示。

图15 面内等效弹性参数与缝线直径的变化关系

图16 面内等效弹性参数与铺层角度的变化关系

由图16可知:与铺层顺序为[0/90/0/90/0/90]的ECSDC 相比,铺层角度对结构面内等效弹性参数的影响比较明显。随着纤维增强阻尼薄膜铺层角度的变化,ECSDC 的弹性模量和剪切模量均呈现出周期为π/2的正弦曲线变化。当铺层角度是45°的奇数倍时,结构的等效剪切模量G12达到最大值。

4 结论

本研究中建立了复合钉贯通的面内纤维折线变形模型,推导了嵌入式共固化缝合阻尼复合材料面内等效弹性参数的数学表达式,并通过ANSYS 有限元数值模拟和文献对比验证了该理论模型的准确性,进一步研究了缝合密度、缝线直径和铺层角度对 ECSDC 结构面内等效弹性参数的影响,为该结构的动力学与几何非线性研究奠定基础。主要结论表明:

1) 由于富树脂区、面内纤维偏转和纤维损伤等因素的影响,缝合后的 ECSDC 结构较缝合前复合材料的面内等效弹性参数有所降低,但结构的各向异性得到了增强;

2) 当缝线直径和铺层角度不变,ECSDC 结构的面内等效弹性参数会随缝合密度的增大而降低;

3) 当缝合针距、缝线行距和铺层角度不变,ECSDC 结构的弹性模量和剪切模量随缝线直径的增大而降低;

4) 当各缝合参数和蒙皮铺层角度不变,随着纤维增强阻尼薄膜铺层角度的变化,ECSDC 的弹性模量和剪切模量均呈现出周期为π/2的正弦曲线变化。当铺层角度是45°的奇数倍时,结构的等效剪切模量G12达到最大值。