预制破片对2种姿态人体目标的毁伤效果研究

符振荣,樊文欣,李瑞青,杨连新,王玉帅,陈 燕

(1.中北大学 机电工程学院,太原 030051; 2.中北大学 机械工程学院,太原 030051;3.中国人民解放军63856部队, 吉林 白城 137001; 4.陆军装备部驻北京地区军事代表局某军事代表室, 太原 030009)

0 引言

近年来地区冲突频发,战争中的人员损伤问题突出,研究武器对人员的毁伤效果,对武器的威力评估及战场火力调控、精确打击目标有重要意义。

武器攻击地面目标,通过毁伤函数计算得到毁伤概率分布称为毁伤矩阵。文献[1-4]介绍了几种毁伤函数,丁贵鹏等[5]采用Carlton毁伤函数结合Monte Carlo法,构建毁伤矩阵,对杀伤榴弹的效能进行评估。田浩成等[6]提出了改进的毁伤矩阵,基于A-S人体失能准则,计算出更加准确的失能概率分布。

1965年,美军导弹实验室的Allen和Sperrazza对人体躯干解剖截面进行了易损性分析,结合创伤弹道学的研究,拟合出了A-S准则,已经广范应用于美军的人员目标毁伤效能评估程序[6]。理论上,A-S准则主要用于单人目标失能概率的计算。

针对地面集群目标,国内主要采用杀伤面积为指标进行评估,杀伤面积是杀伤概率的加权面积[7-8]。杀伤概率的计算通过统计每个目标网格内的有效破片个数,代入公式计算,计算过程比较简单,相比于A-S准则,没有考虑破片的击中部位、破片速度、破片质量以及不同躯体部位的易损程度等因素的影响。

目前,国内对毁伤矩阵的研究很少,未见有论文文献通过毁伤矩阵的方法去研究预制破片对不同人体姿态的的毁伤效果。

为此,本文中详细阐述了A-S失能准则及毁伤矩阵的构建方法,以预制破片作为研究对象,设置不同落角、炸高与落速,改变人体姿态,包括站姿与蹲姿,对比分析预制破片对不同人体姿态的毁伤效果。

1 失能概率计算

1.1 单枚破片命中

A-S失能准则认为人体的生理功能是由各个器官相互协调、配合实现的。由于每个器官功能不同,破片击中不同人体部位所造成的损伤程度不同,导致的失能程度也不同。所谓的“失能”是指:战场人员在规定时间内失去执行规定战斗任务的能力,即丧失战斗力[9]。美军分为防御30 s、进攻30 s、进攻5 min等,这表征执行不同战斗任务人员在规定的丧失战斗力的时间内,被特定(质量、形状、速度)破片命中后,丧失战斗力的程度[10]。

根据人体创伤弹道学的研究[10],A-S失能准则根据不同损伤部位,在概率计算中,赋予不同的系数,同时考虑单个破片的质量、速度,准确计算出人体的失能概率。其具体表达式为:

Ps=1-exp[-a(mv3/2-b)n]

(1)

式(1)中:m为破片质量,单位为格令;v为破片击中人体时的速度,单位为英尺每秒;a、b、n为不同损伤部位下的系数,如表1所示;b为造成失能的阈值。

1.2 多枚破片命中

战斗部爆炸产生破片群,对人体的伤害可能包括许多枚破片,会命中人体的不同部位,需要计算多枚破片对人体造成的总失能概率。假设每一枚破片的运动过程和造成的失能情况独立。计算多枚破片对人体的失能概率,计算公式为:

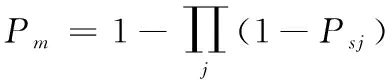
(2)

式(2)中:Psj为第j枚破片命中人体造成的失能概率,可通过式(1)计算得到;Pm为多枚破片导致的总失能概率。

表1为防守30 s对应的a、b、n系数,下面的研究以防守30 s为条件进行计算。

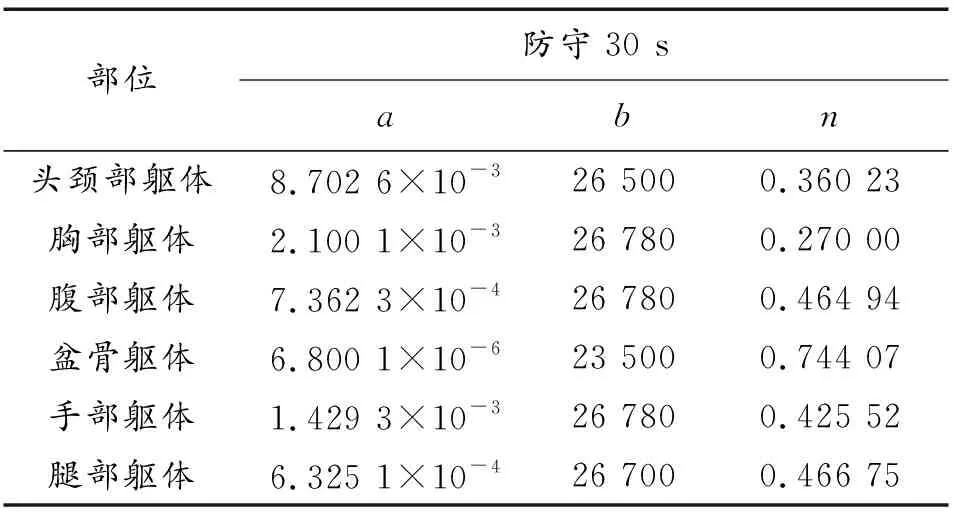
表1 A-S准则系数

2 构建毁伤矩阵

2.1 计算流程

计算流程如图1所示。

2.2 破片飞散数值模拟

战斗部结构如图2所示,口径为35 mm,包括预制破片、内衬、外壳、上下端盖、装药、空气域。预制破片材料采用45号钢,共25层,每层36个破片,共900个破片。使用ALE流固耦合的方法[11],采用顶端中心起爆。

静爆破片场如图3所示,分布呈灯笼形,速度区间为1 000～1 500 m/s。

图3 破片场分布

2.3 人体模型

如图4所示,建立可调节姿态的人体模型,站姿时身高为170 cm。士兵受到炮火袭击时,常采用下蹲姿态和双手抱头的动作,保护身体不受伤害。因此,设置蹲姿、站姿2种姿态,蹲姿时双手放于后脑处,做保护头部的动作。

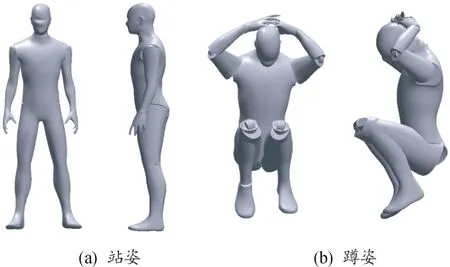
图4 人体模型

人体躯干划分如图5所示,参照A-S准则将人体划分为头颈部躯体、胸部躯体、腹部躯体、盆骨躯体、手和腿等6个部分。

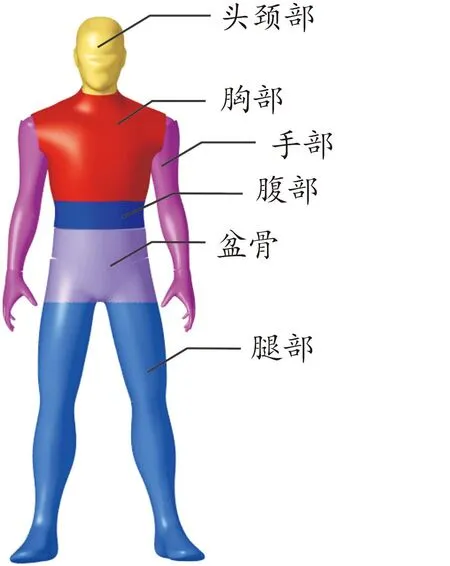
图5 人体躯干划分示意图

2.4 破片射击迹线

破片在空气中受到空气阻力和重力的作用,y轴负方向表示重力的方向,根据质点运动方程可以得到破片的运动方程为[12]:

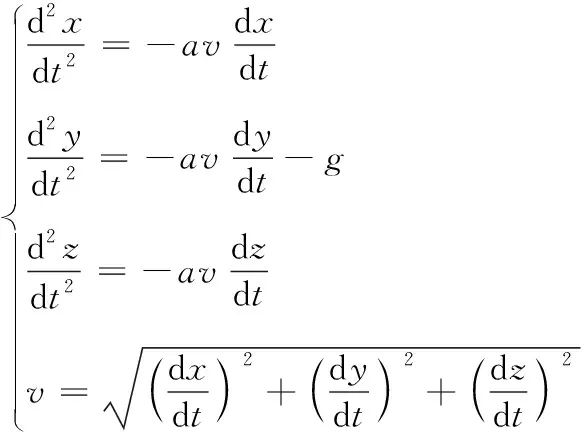
(3)

式(3)中:v为破片速度;a为空气衰减系数;g为重力加速度;t为时间;

从LS-DYNA仿真结果中提取破片的初始坐标、速度等参数,如图6所示,经过坐标变换得到地面坐标系下的破片参数,代入式(3)计算,采用龙格库塔法编程求解,得到随t变化的坐标x,y,z及速度v。

2.5 战斗部-人体目标交会

2.5.1坐标转换

建立如图6所示XdYdZd与XYZ坐标系,以战斗部顶端中心爆点为原点O,建立战斗部坐标系XYZ。Od为点O在地面的投影,以Od为原点建立地面坐标系XdYdZd。O点在地面坐标系XdYdZd的坐标为(H,0,0),X轴与Xd轴相交,角度为落角θ,XY平面与XdYd平面在同一平面。因此,战斗部坐标系绕OZ轴逆时针旋转θ,再平移距离H,即可得到地面坐标系,旋转矩阵M1如下:

(4)

假设在战斗部坐标系下,破片的坐标为(xd,yd,zd),经过旋转θ角度,沿Y轴负方向平移距离H,转换为地面坐标系的坐标(x,y,z),表达式为:

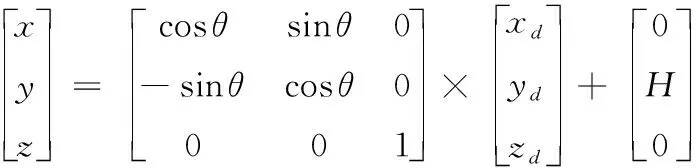
(5)

图6 弹体坐标系与地面坐标系示意图Fig.6 Coordinate system of warhead and ground

2.5.2目标区域网格化

如图7所示,以Od为原点,在地面设定目标区域,将所有破片的射击迹线包括在内,尺寸为L1×L2,将目标区域划分为l1×l2的网格[13]。为了划分过程简便,设置l1为L1的整数倍,l2为L2的整数倍。人体在立姿时,所占地面面积约为0.5,设置L1和L2为14.7,l1与l2为0.7。

图7 目标区域网格示意图

2.5.3人体目标设置

使用Hypermesh在人体表面设置二维网格,以ASCII明码的STL格式导出网格模型。STL格式是用三角面元的集合来表现几何模型。在ASCII码文件中,包含有三角面元的顶点信息,通过Matlab编程读取,使用patch函数将几何模型重构。

确定目标区域L1、L2和网格尺寸l1、l2后,将网格尺寸作为步长,移动人体至每个网格内,如图8所示,结合破片射击迹线,构建战斗部—人体目标交会模型[14]。例如,在落角为80°,炸高为2.6 m,落速为300 m/s,射线与人体的交会,如图9所示。

图8 人体目标设置示意图

图9 射线与人体交会示意图

2.5.4击中部位识别

识别破片击中部位的问题,本质上是射线和三角形面元的相交问题。根据1997年Tomas Moller提出的方法,空间中的一条射线,假设起点为O,方向向量为D,则射线上的任意一点P可以表示为[15]:

P=O+Dt

(6)

类似的,对于3个顶点为P1、P2、P3的空间三角形,如图10所示,其中任意一点P可表示为[15]:

P=(1-u-v)P1+uP2+vP3

(7)

式(7)中:u与v为P2、P3的权重;1-u-v为P1的权重。如果P在三角形内,即满足u≥0,v≥0,u+v≤1。

图10 任意点位置示意图

因此,有如下方程,其中t、u、v为未知数:

O+Dt=(1-u-v)P1+uP2+vP3

(8)

提取t、u、v可得:

(9)

令X1=P2-P1,X2=P3-P1,M=O-P1可得:

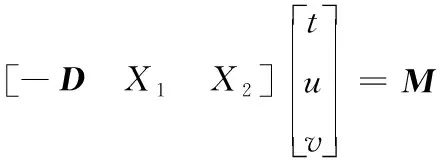
(10)

使用克莱姆法则,可解得:

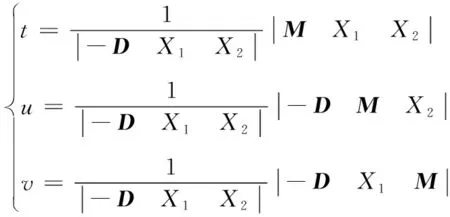
(11)

写成矩阵形式,有:

(12)

根据向量混合积原则,有:

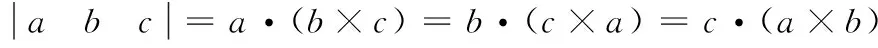
(13)

(14)

可推得:

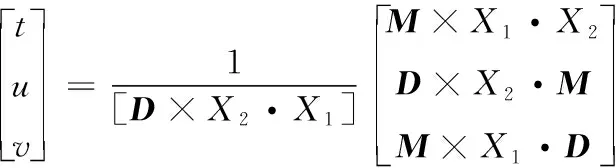
(15)

令L=D×X2,K=M×X1可得:

(16)

通过Matlab编程计算出t、u、v,如果满足u≥0,v≥0,u+v≤1,即射线与空间三角形相交。

2.6 有效毁伤面积

目前大部分研究,通常以杀伤面积做指标评估毁伤效果,与计算杀伤面积的方法类似,2013年Morris[16]提出以有效毁伤面积(MAEF)表征破片战斗部的毁伤效果,计算公式为:

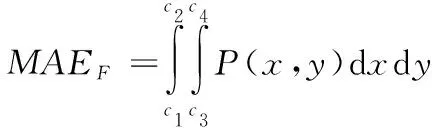
(17)

式(17)中:P(x,y)为每个网格处的失能概率;c1、c2、c3、c4为毁伤区域范围。

3 计算结果

3.1 不同落角下2种人体姿态的毁伤效果

人体姿态为蹲姿和站姿,炸高为2.6 m,落速为300 m/s,计算如表2所示的战斗部终点工况,对比研究2种人体姿态的毁伤效果。该战斗部主要用于步枪榴弹,在一定高度攻击掩体后的敌人时,可能会使用平射,使落角接近0°,因此设置落角为0°,依次递增。

表2 不同落角下终点工况

人体在蹲姿状态,站姿规律类似,如图11所示,随着战斗部落角从0°增加至80°,毁伤面积从22.5 m2增加至44.2 m2。落角在0°、20°,毁伤面积相差不大,如图12(a)所示,对应的破片击中总数量略有波动,落角大于40°时,击中人体的破片总数明显增加,毁伤面积也显著上升。

蹲姿与站姿对比,如图12(a)与图11所示,整体上,站姿的毁伤面积要大于蹲姿,在落角0°与20°,站姿的毁伤面积与蹲姿相差不大,破片击中总数量无明显差距,落角大于40°时,站姿的毁伤面积要高于蹲姿,破片击中总数量也明显高于蹲姿。如图12(b)所示,落角在20°～80°,由于蹲姿下的腿部暴露面积显著减少,腿部中弹数明显减少。手部采用了保护头部的动作,在落角为0°～40°,由于2部分三角面元重叠较多,计算误差较大,头部中弹数上下波动,落角大于40°时,相比站姿,蹲姿下的头部中弹数有明显减少。

图11 不同姿态下的毁伤面积曲线

图12 不同姿态下的破片击中数量

3.2 不同落速下2种人体姿态的毁伤效果

人体姿态为蹲姿和站姿,设置炸高为2.6 m,落角60°的有效破片较多,毁伤面积也较大,设置落角为60°,改变战斗部落速,计算如表3所示的战斗部终点工况,对比研究2种人体姿态的毁伤效果。

表3 不同落速下终点工况

人体在蹲姿与站姿状态,如图13所示,随着战斗部落速增加,毁伤面积先下降后上升。

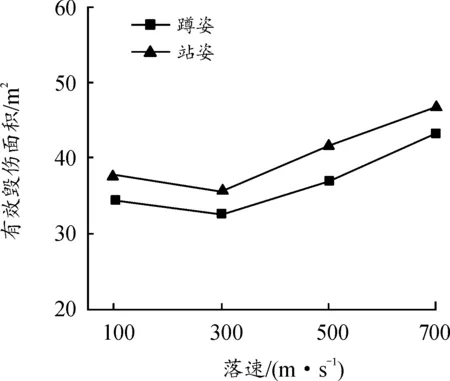
图13 不同姿态下的毁伤面积曲线

从100～300 m/s,战斗部落速方向与战斗部轴线重合,增加落速后,破片飞散方向趋向于轴线,飞散角减小,如图14所示,对应的破片击中数减少,有效毁伤面积减少。落速大于300 m/s时,飞散角减小,对应的破片击中数继续减少,由于A-S准则考虑了破片动能的影响,破片动能的增加抵消了飞散角减小的影响,导致毁伤面积增大。

蹲姿与站姿对比,在4种落速工况下,蹲姿的毁伤面积始终低于站姿,对应的头部、腿部和总的破片击中数也始终低于站姿。

图14 不同姿态下的破片击中数量

3.3 不同炸高下2种人体姿态的毁伤效果

人体姿态为蹲姿与站姿,设置落角为60°,落速为300 m/s,改变炸高,计算如表4所示的战斗部终点工况,对比研究2种人体姿态的毁伤效果。

表4 不同炸高下终点工况表

不同姿态下的毁伤面积曲线如图15所示,在蹲姿状态,高度从2～4.6 m,毁伤面积先上升后下降,在高度2.6 m,毁伤面积为最大32.6 m2。从2～2.6 m,炸高增加,毁伤面积增大,大于2.6 m后,满足动能标准的破片减少(见图16),对应的击中数也减少,毁伤面积下降。在站姿状态,高度从2～4.6 m,毁伤面积先上升后下降,在高度3.6 m,毁伤面积为最大38.8 m2。

人体2种姿态对比,整体上,蹲姿的毁伤面积低于站姿,头部、腿部和总的破片击中数也始终低于站姿。由于蹲姿的人体高度比站姿降低约1 m,蹲姿的毁伤面积峰值提前至炸高2.6 m。

图15 不同姿态下的毁伤面积曲线

图16 不同姿态下的破片击中数量

4 结论

本文中通过构建毁伤矩阵的方法,以2种姿态的人体为目标,在不同落角、炸高、落速下,研究预制破片战斗部对2种人体姿态的毁伤效果,得到如下结论:

1) 随着战斗部落角的增加,2种姿态的毁伤面积和破片击中总数逐渐增大,落角80°时达到最大,与落角0°相比,毁伤面积约1.9～2.2倍,破片击中总数约1.9～2.4倍。采用蹲姿,整体比站姿的毁伤面积减少了6%～16%。

2) 随着战斗部落速的增加,2种姿态的毁伤面积先减小后增加,而破片击中数逐渐下降。采用蹲姿,整体比站姿的毁伤面积低8%～11%,破片击中总数低22%～26%。

3) 随着炸高的增加,毁伤面积与破片击中数先上升后下降,蹲姿的毁伤面积峰值对应的炸高降低约1 m,整体比站姿的毁伤面积低约8%～20%,破片击中总数低22%～36%。