GeoGebra助力高中生直观想象素养的提升*
肖阳芳 徐金润 邵贵明
(黄冈师范学院 438000)
熊建军
(湖北省鄂州高中 436000)
1 问题提出
《普通高中数学课程标准(2017年版)》(下称《课标》)指出,学科核心素养是育人价值的集中体现,是在数学学习和应用过程中逐步形成和发展的[1].提升数学核心素养的教学,重要的是在教学中使学生真正理解、掌握知识,并能灵活运用,在这个过程中,使他们掌握数学思想方法和提高思维能力,达到知其然且知其所以然[2].
在科技迅猛腾飞的今天,我们如何在教学实践中使学生知其所以然?如何提升学生的直观想象素养呢?比如对抽象的立体几何内容,学生难以理清几何结构各要素关系;对于习题中的动点最值问题,学生难以想象出动点轨迹及数量关系,这都是提升直观想象素养的绊脚石.
鲍建生对几何教学提出建议,认为几何教学应该建立在直观经验的基础上[3].范希尔曾说过,假如能呈现对直观的洞察,应有助于学生学习抽象的几何概念.如若将信息技术与数学课堂有效融合,优化教学生态,为学生理解知识本质提供直观模型,给学生提供探索实验的环境,培养学生几何直观、空间感以及几何作图方法,可切实提升学生的核心素养.
2 GeoGebra辅助数学教学对提升直观想象素养的重要性
笔者在对一线教师关于提升学生直观想象素养的访谈中发现,他们主要希望运用动态几何软件辅助教学解决两部分问题:一是借助动态几何软件,依托教学内容,比如立体图形的外接球和内切球问题、立体图形的截面问题等,让学生直观感受复杂几何体的生成过程,并理解图形之间的内在联系,把抽象的空间图形直观化;二是对于立体几何中动点、动直线引起的最值问题,希望借助软件的特定功能,将动态问题可视化、具象化,发展学生的空间认知和想象力,能用平面图形描述问题和解决问题.
GeoGebra(下称GGB)是一款能同框呈现代数与几何关系的动态几何软件,揭示数学各要素之间复杂的动态逻辑关系,重要的是其与使用者具有高度的互动性,使用者可以通过“旋转—拖曳”功能,依自己的目标和想法操作几何对象以观察存在于其中的性质或关系,不同功能区可以同步交互,实时观察,呈现数学知识的多元表征,具有直观便捷的特点[4].且GGB官方网站提供在线教学资源平台及操作教程,使得各学科阶段都能交流使用.施良方曾提出运用教学媒体进行声像呈示,可以使学生各种感官得到延伸,把学生的感官难以感觉到和不可能感觉到的事物、现象、事件,直观、形象地再现给他们,拓展学生认识客观世界的时空广度.同时声像呈示还可改变知识的抽象、概括化层次,适应学生的认识发展水平,便于学生接受[5].本文展示了GGB在提升学生直观想象素养方面的作用和魅力.
3 教学过程展示
数学教学中,学习新知和解决习题都是提升学生直观想象素养的有效载体.多面体的外接球问题涉及球与多面体的双边知识,它虽然已经被教科书删除,但每年高考都会出现有关球外接和内切的问题.而传统教学方式对这类知识通常教以秒杀秘籍或答题模板,学生也普遍缺乏空间想象力,更是对这类知识一知半解,这使得学生直观想象素养的提升较为困难,所以选用外接球问题的知识生成和习题探索作为提升学生直观想象素养的发展点是合适的.
3.1 折叠模型的知识生成
下面以外接球的折叠模型为载体,借助GGB展示几何体的生成过程.折叠模型是指将等腰 三角形进行拼接或将菱形以对角线折叠出来的立体图形.如图1,在三棱锥A-BCD中,△ABD和△CBD均为边长为2的等边三角形,且二面角A-BD-C为120°,则三棱锥A-BCD外接球的表面积为多少?根据球的表面积公式S=4πR2,若知半径便得表面积.

图1 构造多面体
对于这类问题,学生很难想象出外接球怎样与三棱锥相接,现用数学动态几何软件直观感受图形元素的生成过程.在GGB中先画出立体图形(图1),接着在指令栏输入“外接圆(B,C,D)、外接圆(A,B,D)”,再选择“中点/中心”工具,得出两外接圆圆心(图2).
外接球球心是以各自圆心为垂足作垂直于外接圆的垂线的交点,输入命令“垂线(E,poly1)” “垂线(F,poly2)”,3D绘图区出现两条垂线,代数区显示“直线g、直线h”.用“交点”工具点选直线g和直线h,代数区显示“点O”,该点即为折叠模型外接球的球心.在代数命令区输入“球面(O,A)”命令构建外接球(图3).

图3 展示外接球
将交点O与点C连接,OC为球半径.根据题目要求和已知条件进行分析,在3D绘图区连接待用线段,隐藏无关变量(图4).
将空间问题平面化,运用等量关系建立等式求结果.这时,我们便通过GGB将立体几何问题完整地、直观地转化为平面图形问题.
因为折叠模型具有一般性,教学中教师可以使用软件功能改变模型折叠的角度,或者通过软件的放缩、拖曳功能改变图形的大小,实时了解动态变化的折叠模型,抓住变化中的不变量;学生也可以从自身的疑惑点出发,运用旋转视图和移动视图操作、观察几何元素,借图形直观认识数学问题、表达数学问题,启迪解决此类问题的思路,以达到对这类模型的本质理解.同时让学生感受几何关系的形成过程,给学生未来进行空间想象提供范式,提高数形结合能力,从而提升学生的直观想象素养.
3.2 外接球问题的习题探索


图5 正四棱锥体积变化图

根据球心是过两截面圆的圆心作垂直于各截面圆的垂线的交点这一定义,在GGB中输入指令“外接圆(E,B,C)”,再选择“中点/中心”工具,显示外接圆的圆心G.选择垂线工具,依次点选点G和△EBC,绘图区出现一条垂线.用“交点”工具选择垂线和正四棱锥的高,即得点O,这点为外接球的球心.输入“球面(O,D)”,绘图区显示正四棱锥的外接球(图6).
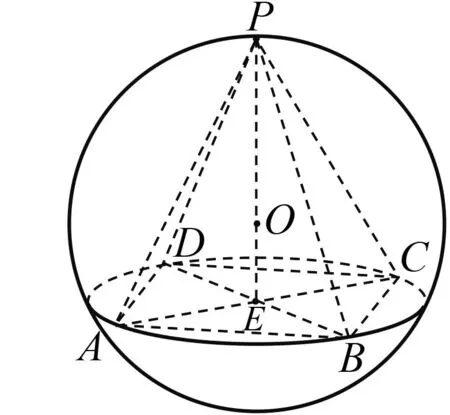
图6 正四棱锥外接球展示
引导学生通过旋转、放大功能对图形进行交换,观察并结合已有知识可发现,外接球的球心位于高所在的直线上,同时正四棱锥的高、侧棱长和底面对角线构成直角关系.将空间位置平面化,根据已知的等量关系求得结果.用GGB软件帮助学生打开思维,渗透数形结合、空间问题平面化等数学思想方法,引导学生在关联的情境中构建相应的几何图形,用图形探索解决问题的思路,这恰恰是课标对直观想象素养提出的水平要求.
4 结束语
数形结合是一种特殊的能力.借助GGB能展示数形变化之间的相辅相成,基于视觉的观察能感知数学对象并加深对图形变化的理解.通过视觉方法与几何方法的交互作用,为学生学习几何概念和结构创造环境、提供工具,同时运用GGB的拖曳和旋转功能,在可视化、具象化的数学实验环境中感受知识生成和问题探索,学习如何从直观展示中形成解题思路,如何找寻问题解决的关键.本文呈现的样例是静态操作,教师在教学中应遵循主体性、启发性、探究性、趣味性、适度性原则,有效地将GGB软件与数学课堂融合,希冀让学生感受突破思维阈限的过程,提高几何直观、空间想象力,使学生知其然且知其所以然,以此提升学生的直观想象素养[6].但在具体教学中,GGB只能作为一种辅助教学的工具,要使教学有意义,需要先了解学生是否已经具备了一定的几何知识,否则会损害学生的几何思维.

