问题驱动视角下章末复习课教学设计探究
——以“空间向量与立体几何”为例*
郝文华
(北京师范大学盐城附属学校 224007)
1 引言
近年来,高中数学公开课、优质课、示范课、研讨课等教学活动课的选题,不再以常规的新授课为主,而更偏向于单元起始课、章末复习课、大单元主题教学等课型的设置.对于此类课题,教学设计的难度有所增加,对教师整体把握课程内容要求更高,教学设计与课堂实践存在的问题也较多.特别是章末复习课,不仅具有“综合性、系统性、 问题性、应用性”等特点,同时还承载着“查漏补缺、凝练提升、拓展迁移”的核心任务.常规意义上的“知识点+练习题”的复习模式问题日益凸显,难以达成素养要求.张奠宙先生就曾指出:“公开课中难见好的复习课,大多是大容量、快节奏、高密度的解题训练课.”[1]单元复习课不能单纯地上成习题训练课,不能忽视知识、思想方法间的联系与整合,更不能忽略学生的自主探索与思考,教学设计需高度立意、整体构建、深挖思想、关注思维.本文以2023年6月中旬笔者执教的一节市级公开课(苏教版新教材选择性必修第二册第六章“空间向量与立体几何”章末复习课)为例,探讨如何从“问题设计”的视角进行章末复习课教学设计.
2 课前思考与教学过程
2.1 课前思考
作为市级公开课,一节课复习一个单元内容,自然会想到留与舍、主与次的问题,虽不能面面俱到,却不失结构性与连续性,这就需要整体把握教材内容,提炼数学本质,发掘逻辑关系,构建结构体系,设计授课主线.
(1)教材导引
在高一学习“平面向量”和“立体几何初步”的基础上,继续学习“空间向量与立体几何”.类比平面向量的研究过程,体会平面向量与空间向量的共性和差异.运用向量法研究空间基本图形位置关系及测量问题,感悟向量是研究几何问题的有效工具.
(2)新课标要求
理解空间向量的概念、运算、背景和作用,能够依托空间向量建立空间图形及图形关系的想象力;掌握空间向量基本定理,体会其作用,并能简单应用;能够运用空间向量解决一些简单的实际问题,体会用向量解决一类问题的思路;教学应凸显“几何与代数”的数学本质,即用代数方法研究几何问题,并给出代数结论合理的解释.本章主要培养直观想象、数学建模、数学运算三大学科素养.
(3)学情分析
通过必修第二册“立体几何初步”章节相关基础知识的学习,学生已经具备用判定定理和性质定理来证明平行和垂直问题、用传统方法来求比较基础的空间角问题、用等体积法来求空间距离的能力;通过必修第二册“平面向量及其应用”及选择性必修第二册中“空间向量与立体几何”的学习,学生已经初步掌握了用空间向量解决立体几何问题的基本路径及方法,但对整体把握向量的工具性作用及稍复杂的空间角及距离的求解还需进一步加强.
(4)课时目标
能够正确选择解决空间几何问题的方法(几何法、图形向量法、坐标向量法);能够用向量法解决空间基本位置关系和度量问题.
(5)教学策略
《普通高中数学课程标准(2017年版2020年修订)》也指出,高中数学教学以发展学生学科核心素养为导向,创设合适的教学情境,启发学生思考,引导学生把握数学的本质[2].作为一节单元复习课,为了促进学生形成完整的知识体系,形成教—学—评完整闭环,笔者计划站在大单元的高度组织复习内容,以向量的工具性作用为主线,以合理的问题串驱动教学,通过引导学生自主探讨来促使其进一步掌握用向量解决问题的基本路径,践行“教思考、教体验、教表达”的教学理念.
2.2 教学过程
问题1为什么要引入空间向量?空间向量的主要作用是什么?
设计意图如图1,通过回顾平面向量在平面几何中的应用及立体几何初步的学习,引导学生发现:平面向量解决空间立体几何问题具有很大的局限性,这就要求我们引入空间向量,充分体现引入空间向量的必要性.继而回顾利用空间向量解决立体几何问题的两个方向:一个是研究空间中点线面的位置关系,另一个就是求空间中的距离及夹角.

图1
问题2下列问题所涉及的基础知识你还记得吗?
(1)已知a=(0,1,1),b=(1,0,2),c=(1,1,0),则(a·b)c=.
(2)已知空间向量a=(2,-1,1),b=(1,1,2),则|a+b|=;向量a与b的夹角为.
(3)设a=(1,0,1),b=(0,-1,1),c=(1, -2,x),若三向量a,b,c共面,则实数x=.

设计意图通过4道极为简单的小题来回顾空间向量的相关概念及线性运算,包括数量积的概念、共线与共面定理以及空间向量的基本定理、坐标表示及运算等,引导学生发现:与高一学习的平面向量相比,除了研究维度不同之外,它们具有高度的一致性,可以认为空间向量是平面向量的一个推广与延伸,而且这些内容都是后续学习向量在立体几何中应用的基础.
问题3如何运用向量方法解决立体几何中的求解问题?
例1如图2所示,在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°,求AC1的长.

图2
变式训练 求BD1与AC夹角的余弦值.
设计意图例1主要是通过空间向量“基底法”来解决空间立体几何中的长度及夹角问题,引导学生通过“找基底—表示相关向量—向量运算—得出结论”的基本程序,体会基底法解决立体几何问题的一般路径及向量的工具性作用.
问题4如何运用空间向量坐标法解决立体几何问题?
例2如图3,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,点D,E,F分别为棱A1C1,B1C1,BB1的中点.
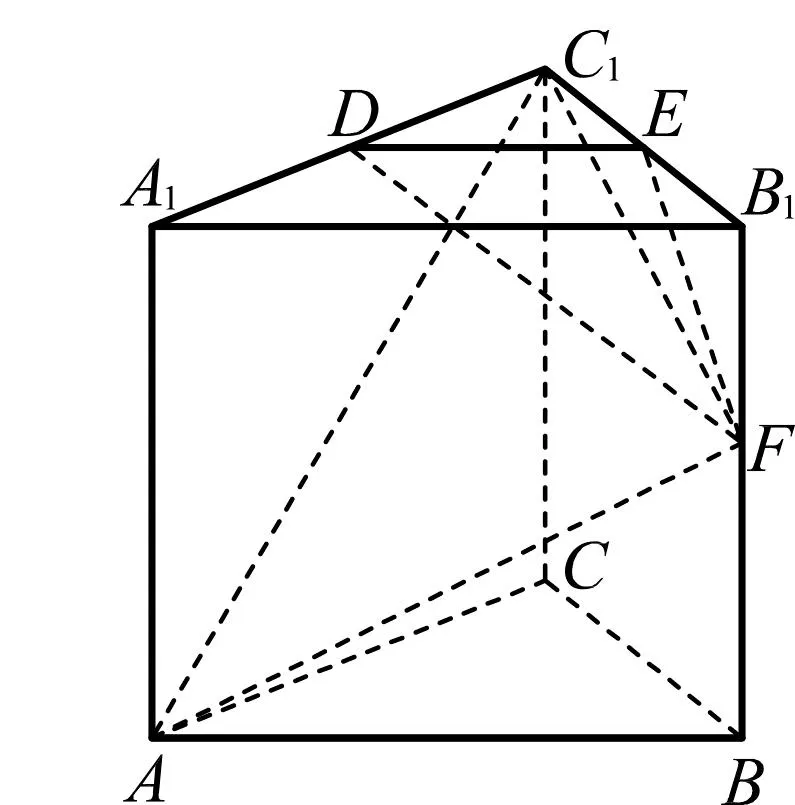
图3
(1)求证:直线AC1∥平面DEF;
(2)求平面AC1F与平面DEF夹角的余弦值.
设计意图第一个小问一般难以采用基底法证明,与例1的方法产生思维冲突,为下一步引出坐标法做铺垫.当然,对于问题(1),证明方法的选取是灵活的,可以先采用综合法(即几何法),然后采用空间向量坐标法,比较两种方法的异同点,而问题(2)可直接建系解决.对于坐标法解决空间角的求解问题,包含线线角、面面角、二面角、线面角四类,空间距离包括两点间的距离及点到线、点到面、线到线、线到面、面到面的距离等多种情况,授课中可采用一题多变、追问等方式来实施教学.

(2)若点F是线段BB1的中点,求点A到平面DEF的距离.
(3)若点F为棱BB1上的一动点(不包括两个端点),求点A1到平面AC1F的距离的取值范围.
(4)在本题中,找出两条异面直线,并尝试利用空间向量坐标法求其夹角及距离.
(5)举例说明:利用向量坐标法还能解决什么问题?请设置一个线面角求值问题,并解答.
设计意图此处5个追问并非简单罗列关系,而是由浅入深、由静到动、由封闭到开放的递进关系,意在通过一个题目的变式来回顾总结通性通法,可切实提升授课效率.
问题5通过本节课的复习,你对本章内容是否有了进一步的理解?
设计意图此问主要用来引导学生发现:空间向量是平面向量从二维空间向三维空间的推广,为我们解决立体几何问题提供了新的视角;利用空间向量的坐标表示,可以把向量问题转化为代数运算,从而建立了几何与代数的联系,体现了数形结合的重要数学思想.
追问对用向量法解决立体几何,你是否有了进一步的感悟?(图4)

图4
设计意图此追问是对向量方法的一个总结,也算是一种课时小结,引导学生发现,利用空间向量解决立体几何问题大体上分为三个步骤,见图5.

图5
3 教学启示
3.1 注重问题链设置的统筹性、连贯性及导向性
单元复习课更应体现前后知识的衔接及思想方法的一致性.通过设置具有一定梯度的问题链,引导学生积极思考,逐层深入,在回顾、类比、冲突、探索、归纳中完成对章节内容理解的整体提升.问题设计时要考虑知识之间的复杂联系,设计的问题应贯穿整个单元的知识内容,并具有一定的指导意义及可操作性,使执教者可以从问题链中归结出授课流程.这就需要教师在教学设计环节统筹把握教学内容,先设置若干个(一般5个左右)提纲挈领的大问题,即教学活动的主线,教师可在这几个“大问题”的主线下,逐步展开教学,以免偏离复习主题[3].在每个大问题下均可设置一定数量的小问题(追问、反问等),用来分解部分教学主题或重难点.
3.2 在追问中发展学生的高阶思维
思维进阶是问题设计的评判标准,即前一个问题的解决能够对后一个问题的学习提供帮助,体现出层层递进的关系[4].本课问题4中设置了5个递进式的追问,它们既涵盖了单元复习的知识点及思想方法,又契合了学生的思维水平.追问的设置应遵循“低起点、易入口、上缓坡、渐递进、有发展”的基本原则,通过追问式的变式教学,多向构建知识体系,提升学生的学习能力,培养高阶思维及学科素养.
3.3 积极探索问题驱动下单元复习课新模式
单元复习课不是对知识点的简单梳理,更不是纯粹的解题训练,而是一种“回顾—贯通—升华”的过程.在理解教材及学情的基础上,如何通过设置合理的问题情境,设计具有逻辑性和适切性、递进式的问题链,不断激发学生的深度思考,切实提升章末复习效率,是单元复习教学值得探索的一个问题.

