跨学科融合的数学教学——苏科版初中数学教材的案例分析与思考*

黄贤明 徐敬元

(江苏省苏州高新区景山实验初级中学校 215129)

数学是研究数量关系与空间形式的基础学科,其方法的普适性、文化的丰富性、应用的广泛性及理性思维的独特性都决定了数学与其他学科间存在着千丝万缕的联系[1].《义务教育数学课程标准(2022年版)》(以下简称《课标》)中优化了课程内容,设置了以综合与实践为载体的跨学科主题学习活动,增强学科间相互关联,带动课程综合化实施,强化实践性要求.事实上,跨学科内容早已分散于数学教学的方方面面．例如,教材的编排中、试题的编制中、教学环节的设计中都有跨学科内容的“影子”.张维忠教授研究了数学教材、中高考试题中的跨学科内容,提出跨学科内容的来源维度包括科学、技术、工程和艺术,跨学科内容的类型维度包括并列型、共享型、蜘蛛网型、连接型和统合型,为后续数学跨学科内容的分析提供了理论框架[2].

研究发现,在初中数学教材中存在着诸多跨学科内容,它们分布在章引言、问题情境、例题、课后练习、阅读材料及数学实验等栏目中.这些跨学科内容的呈现大致可以分为两类:其一,教材利用跨学科内容创设科学情境,旨在让学生从情境中抽象出数学信息,获得数学研究对象;其二,教材以跨学科内容作为问题情境或研究主题,旨在让学生应用数学知识与方法解决其他学科的问题,或应用数学的眼光与思维理解其他学科的奥秘.本文以江苏凤凰科学技术出版社的六本初中数学教材(以下简称“苏科版教材”)为研究对象,从跨学科的教学情境、问题设置与项目学习三个维度具体分析教材中的跨学科内容.

1 跨学科的教学情境:获得对数学知识的独到理解

数学知识并不是凭空产生的,需要教师创设合适的教学情境与问题,引导学生用数学的眼光观察抽象出数学研究对象,并在进一步探究中获得对知识的本质理解.情境的创设是多样化的,具体可分为现实的、数学的与科学的三类.对于某些数学知识而言,科学的情境更符合学生的认知经验,更利于学生建立不同学科知识之间的联系.因此,在教学实施中,教师可以把握教材中所选择的跨学科内容,创设跨学科情境,让学生在情境探究中经历科学探究的完整过程,获得对数学知识的深刻理解,从而夯实“四基”,提升“四能”,发展数学抽象、逻辑推理、数学建模等数学学科核心素养.

1.1 用数学的眼光观察跨学科情境

案例1“主视图、左视图、俯视图”与“直线与圆的位置关系”的跨学科情境创设.

苏科版教材七年级上册“5.4主视图、左视图、俯视图”创设了如下情境:

横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.

——苏轼

苏科版教材九年级上册“2.5直线与圆的位置关系”创设了如下情境:

山水相接的地方出现了一道红霞.过了一会儿,那里出现了太阳的小半边脸.慢慢儿,一纵一纵地使劲儿向上升.到了最后,它终于冲破了云霞,完全跳出了海面.

——巴金

教材以诗词与文学作品作为教学情境,并附上相关图片,旨在让学生用数学的眼光观察它们背后所蕴含的数学本质.例如,苏轼的《题西林壁》描绘了千姿百态的庐山风景,揭示了“从不同角度观察物体,所看到的图形往往不同”的内涵.在教学中,教师可以让学生感受诗词中的意境,引导学生用数学的眼光品味诗词内涵,并提问:“生活中你有类似的体验吗?从数学的角度,我们通常从哪些方向观察物体呢?”自然地导入本节课对三视图的探究.再如,巴金的《海上日出》描绘了日出这一伟大奇观,旨在将太阳与海平面视作圆与直线,将日出的过程抽象为直线与圆的位置关系.针对该情境的教学实施,教师可以设计“根据所给文字,描绘日出的简图”的活动,引导学生把握好情境中的关键节点,即日出前、日出时和日出后,并给出日出图片加以参考,让学生绘制出直线与圆相交、相切和相离的示意图,开启对圆与直线位置关系的探索.在教学中,学生经历了以文学为主题的跨学科内容的抽象过程,提升了用数学眼光观察现实世界的能力,发展了数学抽象、直观想象等核心素养,提升了数学探究兴趣.虽然文学与数学的跨学科交融在教材中的案例相对较少,但它们间的碰撞是感性思维与理性思维的碰撞,往往会擦出不一样火花,增添数学课堂的人文趣味.

1.2 用数学的思维思考跨学科情境

案例2“正数与负数”的跨学科情境创设.

苏科版教材七年级上册“2.1正数与负数”的导入环节中给出了四张图片,分别对应着如下三个跨学科内容.

①地理知识:珠穆朗玛峰海拔8 848.86 m,艾丁湖海拔-154 m.

②物理知识:水、水银、酒精的凝固点分别为0 ℃,-38.87 ℃,-117.3 ℃;沸点分别为100 ℃,357 ℃,78 ℃.

③社会知识:2009年末,上海市常住人口 1 921.32万,常住人口自然增长率为0.27%,其中户籍人口自然增长率为-0.102%.

教材给出的跨学科内容旨在引导学生感受现实生活中负数的实例,并提出问题:“你知道上面图片中8 848.86,-154,-117.3,-0.102%这些数的意义吗?”让学生从原有认知结构中提取出相关知识与经验,并用数学的思维思考和解释负数在跨学科内容中的内涵与意义,建立数学与现实世界的联系,抽象出负数与相反意义的量的概念[3].对上述跨学科情境的探究,充分激活了学生的已有经验,促使学生在情境的抽象中提取负数的共同属性,获得了对负数及相反意义的量的本质理解,感受了负数的生活价值与应用价值,促使学生的抽象能力得到了发展.

1.3 用数学的语言表达跨学科情境

案例3“平面直角坐标系(3)”的跨学科情境创设.

苏科版教材八年级上册“5.2平面直角坐标系”第3课时中创设了如下情境:

由电脑控制的机械手把各种元器件准确插入线路板上的焊孔,然后通过焊接工序将它们焊牢.如图1,点A,B是线路板上的焊孔.如果你是工程师,那么你怎样向机械手下达指令,使它把元器件准确插入相应的焊孔?

图1

数学为人们提供了一种描述与交流现实世界的表达方式.在该情境的教学中,首先需要提取情境中的相关信息并将其转化为数学问题,即“如何描述A,B两点在线路板上的位置”.而后学生可以结合已有经验,将问题与平面直角坐标系建立联结,进而产生“建立平面直角坐标系,用点的坐标来确定位置”的思想方法,最终建系解决该问题.该过程既体现了平面直角坐标系知识的运用与迁移,彰显了建系思想方法的发生与发展的完整历程,促进学生形成对知识的深入理解,又使学生感悟用数学语言表达现实世界,锻炼了学生数学化与数学应用的能力,利于学生科学素养的养成.

2 跨学科的问题设置:促进数学知识的迁移应用

问题是数学的核心,是驱动数学发展的原动力.希尔伯特曾说过:“一门学科如果能不断提出问题,那它就充满活力.”在数学发展的历史长河中,数学常与物理、天文、化学等学科相伴,它们相辅相成、相互促进,这就使一些跨学科问题应运而生.在这些跨学科问题的解决中,需要学生把握其他学科与数学的联系,用数学的眼光观察跨学科问题、用数学的思维思考跨学科问题、用数学的语言表达跨学科问题,促使数学知识在跨学科问题的解决中得到迁移与应用,发展学生的数学抽象、逻辑推理、数学运算等核心素养.

2.1 用数学的眼光欣赏跨学科问题

案例4用数学的眼光欣赏艺术的奥秘．

苏科版教材九年级下册“6.2 黄金分割”一课中给出了如下的素材:

“黄金分割”给人以美感,它在建筑、艺术等领域有着广泛的应用.我国的国歌歌词是散文式的自由体新诗,作曲家聂耳在谱曲时,创造性地将它谱成由6个长短不等的自由体乐段.歌曲高潮部分在结构上几乎正好是全曲的黄金分割位置,音乐富有动力,让人感到振奋无比.你能举例说明黄金分割在生活中的应用吗?

该段文字以国歌为例阐述了黄金分割在音乐中的具体体现．在教学实施中,教师可以播放具体的音乐片段,让学生在对音乐的欣赏中用黄金分割的视角感受音乐背后美的原理.而后,教师可以将音乐可视化,让学生在五线谱的音符变化中发现黄金分割点,感受音乐中的美的奥秘.此外,在“黄金分割”的探究中,教师还可以呈现绘画中的黄金分割(如《蒙娜丽莎》)、雕塑中的黄金分割(如《断臂的维纳斯》)、建筑中的黄金分割(如东方明珠广播电视塔),让学生在发现美、欣赏美、感悟美、表达美等多种活动中发展审美能力,提升用数学的眼光欣赏艺术美的能力．

当然,教师还可以开发教材中相关教学内容(如轴对称图形、中心对称图形、平面图形的镶嵌等),选取合适的教学素材,开展艺术主题的跨学科学习,将美育渗透于数学教学之中,实现以美促德、以美启智、以美育人[4].

2.2 用数学的思维思考跨学科问题

案例5用数学的思维解决物理问题.

苏科版教材八年级下册“11.3用反比例函数解决问题”练习第2题:

公元前3世纪,古希腊学者阿基米德发现了著名的“杠杆原理”.杠杆平衡时,阻力×阻力臂=动力×动力臂.

(1)几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1 600 N和0.5 m,设动力臂为l,动力为F,写出F与l的函数表达式,小明只有500 N的力量,他该选择动力臂为多少的撬棍才能撬动这块大石头呢?

(2)阿基米德曾豪言:“给我一个支点,我能撬动地球.”你能解释其中的道理吗?

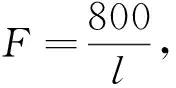
此外,教师不应拘泥于对该题的思考,还可以结合学生所学的物理知识,让学生用数学的思维思考“为什么有的台灯的亮度可以调节?”“为什么推土机的轮子要安装又宽又长的履带?”“为什么打针用的针头是尖的?”等生活中的现象,真正让跨学科内容在解释生活现象中的价值与作用得以发挥,促进学生跨学科素养的发展.

2.3 用数学的语言解释跨学科问题

案例6用数学的语言解释生物现象.

苏科版教材九年级下册“8.6收取多少保费才合理”阅读材料:

据史料记载,在种植的564株第三代豌豆中,开白花的有141株,开粉红花的有291株,开红花的有132株.人们不难看出,实验所得出的3个数字之比近似等于1∶2∶1.怎样解释这一现象呢?

假设第一代开白花的纯种豌豆的基因是WW,第一代开红花的纯种豌豆的基因是RR,则第二代杂种豌豆的基因是WR.再由第二代杂种豌豆彼此授粉会出现如下表1的结果.

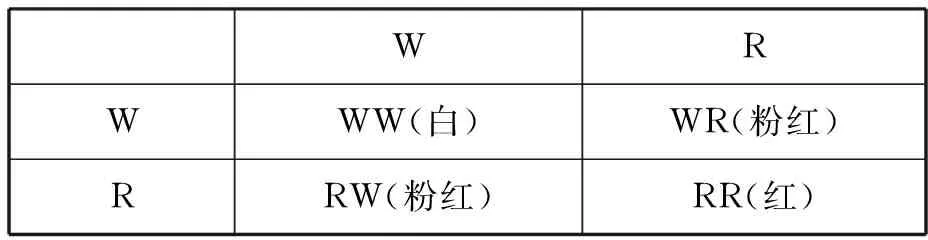
表1

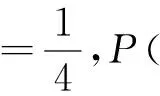
这段材料以孟德尔遗传实验为背景,给出了相关实验数据与实验现象,并指出了该现象的数学原理.学生首先需要将问题数学化,即将问题转化为“求第三代豌豆不同开花情况的概率”,其次通过列表的方式列举出所有的开花情况,在四种结果是等可能的情况下,得出不同开花情况下的概率,最后发现用概率得到的结果与实验情况相吻合,进而解释了这一生物学现象的数学原理.

该材料用数学的语言和方法解释了生物学中的遗传规律,促使学生在阅读理解中感受概率知识在跨学科问题解决中的迁移与应用,获得对概率知识的跨学科价值的认同,有利于学生用数学语言表达跨学科问题能力的发展.

3 跨学科的项目学习:推动数学知识的创新发展

跨学科项目学习是指以跨学科主题的问题解决活动为主线,将数学知识与其他学科领域相连接,为学生创设有意义的项目活动,使学生在活动中通过解决有价值的问题,积累丰富的数学活动经验,创作生动的数学产品,探究并领会数学与其他学科的联系[5].因此,开展跨学科项目学习是实现数学课程目标的重要举措,也是培育学生数学核心素养的重要途径,在实现立德树人根本目标的道路上发挥着重要作用.但传统教育恰恰忽视了这方面内容,这就使得教材中项目内容的编排偏少,教师组织项目活动的经验匮乏,学生参与项目活动的兴趣不高.为此,教师要积极研读《课标》与教材,理解《课标》中项目学习的要求与示例,把握教材中项目学习的相关素材,让跨学科项目学习与教学内容自然衔接,有效发挥跨学科项目学习的教育价值.苏科版教材九年级上册的课题学习栏目以“收集数据、分析数据、探索规律”为主题,给出若干探索事物规律的跨学科课题,包括:利用树叶特征对树木分类、我国GDP与出口总量的关系等.教师可以对教材中的素材进行开发与优化,设计跨学科项目活动,组织学生运用信息技术、书籍、网络等工具,以小组合作探究的形式进行探究学习.

案例7国内生产总值(GDP)调研的项目活动.

教师在项目活动前布置如下的课前任务单.

课前任务单:自改革开放以来,我国经济得到了飞速发展,国内生产总值(GDP)逐年上升.GDP是衡量一个国家或地区整体经济状况的重要指标,那么改革开放以来我国的经济发展有何变化趋势?哪些因素会影响GDP的增长呢?能否应用已有的知识来研究这些问题呢?请你自主查阅相关资料后完成以下三个任务.

任务1 了解GDP的概念,并用具体事例表述GDP.

任务2 查询国家统计局公布的数据,收集我国自1978年以来的GDP数据,思考如何用数学知识来研究GDP的变化趋势,并说明理由.

任务3 分析GDP的增长会与哪些因素存在关系,并收集相关数据.

活动前,学生展示课前任务单完成情况,教师引导学生解决可能面临的困难.而后学生分组,并拟定研究的子课题,例如:探究改革开放以来我国的经济发展变化趋势、探究GDP与居民人均可支配收入的关系、探究GDP与进出口总额的关系等.活动中,学生根据已收集的数据,利用Excel、Mathematica等软件进行数据分析与模型拟合,得出研究结果,填写项目成果单.活动后,小组展示项目成果,形成项目总结.

在课题“探究改革开放以来我国的经济发展变化趋势”的活动中,小组成员收集了1978年以来的GDP数据,以改革开放后的时间为横坐标、国内生产总值为纵坐标,绘制出散点图(图2),观察GDP变化趋势,再选择合适的曲线进行拟合.经过对不同函数模型的比较,小组最终选择了四次函数模型进行拟合(图3),此时的相关系数较高,且所得模型便于后续运算.由函数解析式可以得到:当x=44时,y≈1 228 566.1,当x=45时,y≈1 319 510.5,即可以预测2022年、2023年我国GDP约为122.86万亿元、131.95万亿元.

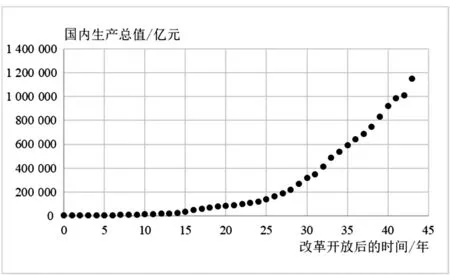
图2

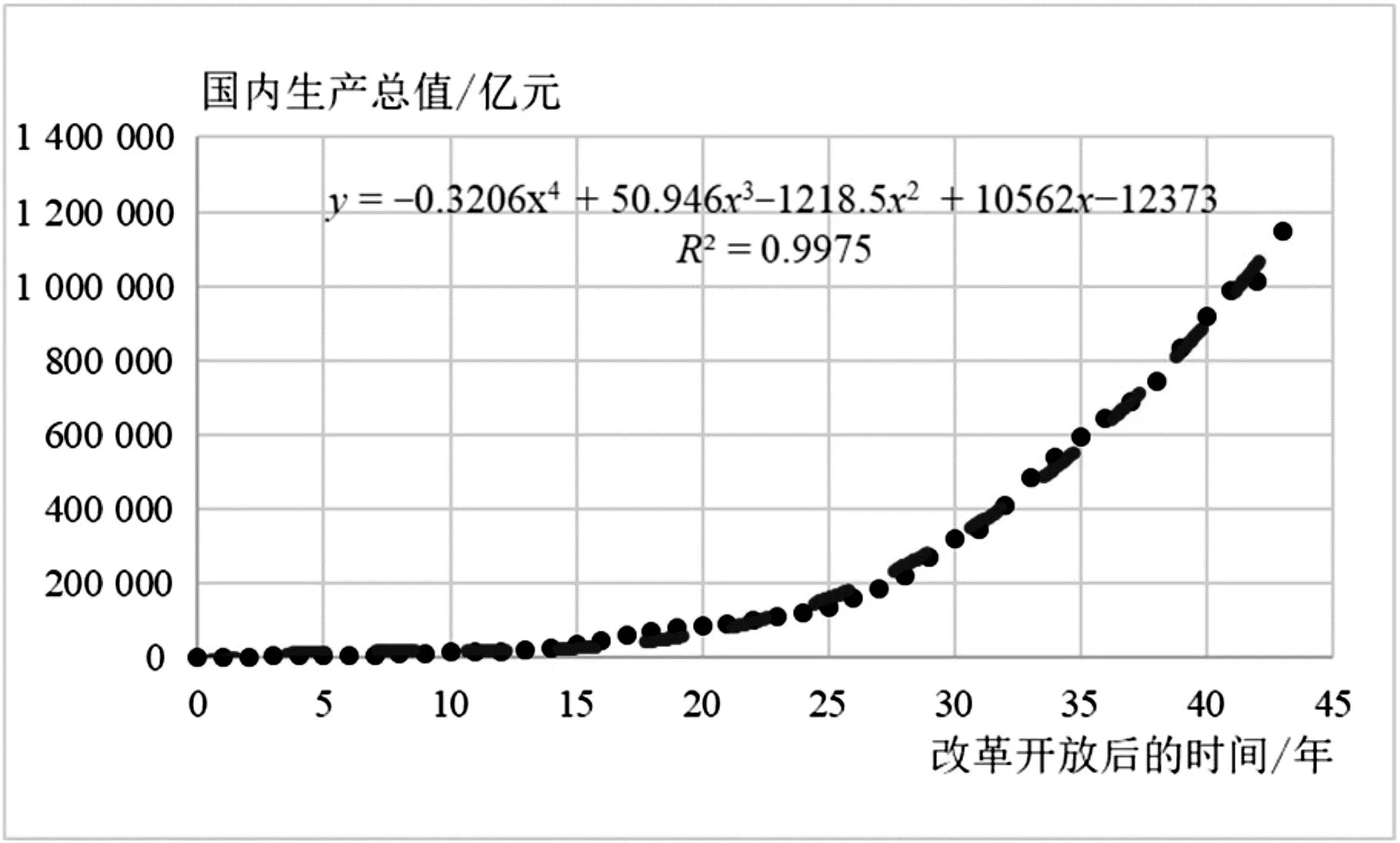
图3

在活动总结中,教师可以整合各个小组的研究成果,引导学生根据数据分析结果解释我国经济发展情况,并从经济与社会发展的视角反思GDP与社会可持续发展等深层次问题[6].虽然学生在活动中所得结果的误差相对较大,但是经历了数据收集、数据分析、软件绘图、函数拟合、选取模型、预测结果等一系列过程,学生了解了经济学、统计学等领域的知识,获得了用统计语言表达事物规律的方法,明晰了科学探究的过程,提升了综合实践能力与信息素养,发展了模型观念与数据观念.

4 结束语

教材是教师开展跨学科学习的重要参考.苏科版教材虽然呈现了诸多典型的跨学科素材,但就数量分布上看,六本教材中的跨学科素材分布不均,整体数量相对偏少;就内容上看,跨学科内容大多是数学与物理、生物学科的跨界交融,而艺术、技术等跨学科内容偏少,且没有出现化学与数学的跨学科内容;就类型上看,以并列型为主,其他形式为辅.这些现象都说明了教材中跨学科内容仍存在层次不明、深度不够等问题.因此,为避免跨学科内容的教学流于形式,教师可以阅读其他学科的书籍、杂志,不断丰富自身知识结构,提升跨学科素养.当面对不熟悉的跨学科内容时,教师可以虚心向其他学科教师请教,了解不同学科间的差异与联系,以促进不同学科间的深度融合.最后,跨学科内容不能拘泥于教材,教师更应从社会生活中、校园实践中乃至其他学科的学习中发现数学元素,并将其转化为教学形态的跨学科素材,以此组织开展跨学科项目学习活动,促使学生在发现问题、提出问题、分析问题与解决问题中发展关键能力,提升数学核心素养.