计算机模拟在物理化学BET多分子层吸附理论教学中的应用

黄建花，张伟

浙江理工大学化学系，杭州 310018

气体在固体表面的吸附是物理化学课程中“界面现象”章节的重要教学内容之一。和液体表面一样，固体表面层的分子也处于不对称力场中。但是，固体无法像液体一样通过自动收缩减小表面积；固体表面只能通过吸附外部气体或液体分子减小表面分子受力不对称程度，从而降低表面吉布斯函数。根据固体和气体分子的相互作用，气体分子在固体表面的吸附可分为物理吸附和化学吸附。国内大部分物理化学教材均详细介绍Langmuir单分子层吸附理论。该理论基于四点基本假设：(1) 单分子层吸附；(2) 固体表面均匀；(3) 被吸附在固体表面上的气体分子之间无相互作用；(4) 吸附平衡是动态平衡。Langmuir吸附等温式能很好地描述化学吸附及低压气体的物理吸附，即物理化学教材中提到的第I类吸附等温线。

但是大量实验发现随着气体压强升高，气体在固体表面的吸附常呈现多分子层吸附，吸附等温线与Langmuir单分子层吸附理论不符。1938年，Brunauer、Emmett和Teller在Langmuir单分子层吸附模型的基础上提出了多分子层吸附理论，即著名的BET理论[1]。BET理论不仅能描述第I类吸附等温线，还能很好地描述第II和第III类吸附等温线，是目前应用最广的吸附理论，BET法是目前测量固态物质比表面积的标准方法。由于BET理论比较抽象，而且BET公式的推导过程涉及较多数学知识，因此大部分物理化学教材都没有详细介绍BET理论和BET公式的推导过程，而是直接给出BET公式[2–4]。学生只能被动接受BET公式，很难透彻理解BET公式的物理意义。我校应用化学专业和材料化学专业均开设了测量固体催化剂比表面积的综合化学实验，面对不同材料，全自动比表面分析仪输出各类不同吸附脱附等温线和比表面积，学生无法正确分析实验数据，只能生搬硬套。由于学生无法正确理解物质比表面积与结构、结构与性能之间的关系，因此，很难达到预期的教学效果。

笔者参考BET多分子层吸附理论的原始文献[1]及刘国杰和黑恩成教授编著的《物理化学导读》[5]，在课堂教学过程中向学生详细介绍BET多分子层吸附理论和BET公式的推导过程。BET理论保留Langmuir单分子层吸附理论的第(2)、(3)和(4)点假设，只对第(1)点假设作了修正。BET理论认为已被固体吸附的气体分子可通过气体分子之间的范德华作用在垂直方向上吸附其他气体分子，形成第二、第三等多分子层吸附。第一层即固体表面层吸附的吸附热qa与气体分子和固体表面的相互作用相关；第二及以上各层即气体吸附层的吸附均源于气体分子之间的范德华作用，吸附热可视为气体的凝聚热qc。当吸附达到平衡时，逐层的吸附速率和脱附速率相等，即由第i− 1层变成第i层的吸附速率等于由第i层脱附变成第i− 1层的脱附速率。基于上述假设，得到著名的二参数BET公式：

BET公式中的Na是压力为p时的气体吸附量，p*和分别是饱和蒸气压和气体在固体表面的单分子层饱和吸附量，参数c是与固体、气体相关的特性参数，

其中k1和k−1分别是第一层的吸附和脱附常数，k2和k−2分别是第二及以上各层的吸附和脱附常数，kB和T分别是玻尔兹曼常数和以开尔文温标表示的吸附温度。显然c与吸附热相关，吸附作用越强，吸附等温线在低压区上升越快，c值可通过分析BET实验数据得到[6]。BET公式(1)也可以写成，

为了帮助学生正确理解BET吸附理论，笔者结合自身科研特长，在课堂教学过程中结合计算机模拟气体分子在固体表面的吸附脱附过程。通过改变固体表面层和气体吸附层的吸附和脱附常数，分别模拟得到第I、II、III类吸附等温线；结合可视化软件使学生能直观看到气体分子在固体表面的吸附脱附动力学过程，从而正确理解BET多分子层吸附理论和Langmuir单分子层吸附理论，为后续综合化学实验提供知识储备。此外，计算机模拟速度快、成本低、不受实验条件和课堂教学时间限制，学生随时可以通过在计算机上调整各种参数模拟各类体系，从而深入理解各知识点，计算机模拟辅助化学教学能有效提高教学质量[7–12]。例如，为了帮助学生正确理解碰撞理论和过渡态理论，赵力维博士等[7]在亲核取代反应机理的课堂教学中，引入商用Gaussian 09计算化学软件计算氯离子与溴代甲烷的一步亲核取代反应中的能量变化和反应途径，通过Gaussian View软件对反应物、活化络合物和生成物结构实现可视化，从而帮助学生直观理解亲核取代反应机理。PHREEQC软件也被用于课堂教学中构建多种化学过程的反应模型，增进学生对化学反应动力学的理解[8]。X射线衍射和拉曼光谱是分别表征物质的晶体结构、化学键及分子振动等微观信息的重要分析技术，这些微观信息肉眼无法观察，对学生而言过于抽象。温大尉博士[10]将免费的晶体学软件和第一性原理计算软件引入课堂教学中，把抽象难懂的微观信息以可视化的形式在计算机上实时展现，帮助学生深入理解物质的微观结构。计算机模拟还能将宏观的色谱分离抽象成粒子在色谱柱中的微观运动，直观展现待分离粒子在色谱柱内的扩散行为，帮助学生理解色谱分离原理[12]。山东大学苑世领教授等[9]利用商用Materials Studio软件开设了计算化学实验，旨在帮助学生从分子水平理解物质的结构–性质关系，培养学生从微观角度理解宏观现象，并解决化学问题的能力。

本文将计算机模拟技术引入到抽象难懂的BET吸附理论的课堂教学中，通过自编程序模拟气体分子在固体表面的吸附，结合实时可视化使学生直观看到气体分子在固体表面的吸附脱附动力学。在物理化学课程之前学生已学习了“C语言设计”和“C语言设计实训”两门必修课，部分学生还选修了“Python语言程序设计”等编程课程，因此学生已具备一定的编程能力。笔者的科研方向为高分子体系的计算机模拟，拥有丰富的编程经验，可以引导学生修改程序并合理调整参数模拟各类吸附等温线，从而更好地理解BET理论及其应用原理。

1 计算机模拟气体分子在固体表面吸附

1.1 模型和模拟方法

模拟在立方格子上进行，固体表面由L×L的格点组成，气体分子落在格点上。气体的压强与气体分子数密度n成正比，即p=nkBT。气体以平均速度＜v＞向各个方向随机运动，气体分子的运动、吸附、脱附用Monte Carlo方法模拟，假定气体分子在每个Monte Carlo模拟时间(1/＜v＞)运动一个格点长度，那么每个Monte Carlo模拟时间有M=nL2/6个气体分子向下运动到固体表面或吸附层表面。格点长度作为长度单位，L可随模拟体系的尺寸而调整，本文选取L= 50。模拟系统的高度没有限制。

气体分子可吸附在固体表面或吸附层上方，吸附的气体分子也可以沿垂直方向脱附但没有水平方向的移动。气体分子吸附到固体表面层(称为第一层)的吸附常数为k1，气体分子从固体表面层脱附的脱附常数为k-1；同理，气体分子吸附到其他气体吸附层的吸附常数为k2，气体分子从气体吸附层脱附的脱附常数为k-2。这些吸附、脱附常数与固体、气体的性质相关，它们的取值没有直接关联。图1是气体分子在光滑固体表面的吸附脱附示意图和程序设计图。每一个格点的吸附气体数目设为N(x,y)，N= 0代表空白表面；N(x,y)的平均值即为单位面积的气体吸附量Na。当取k2=k-2= 0时，我们可以模拟Langmuir单分子层吸附。

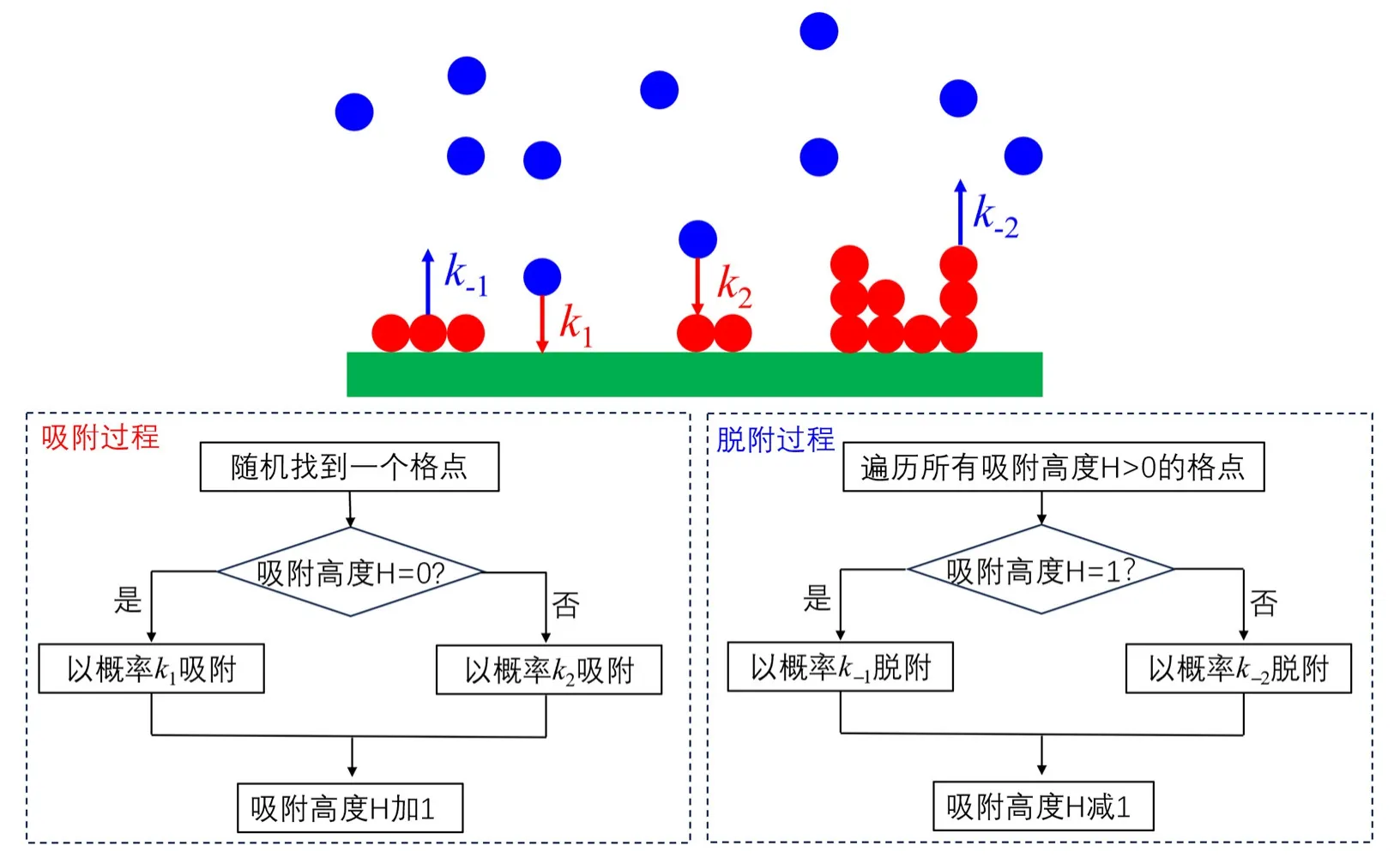
图1 气体分子在光滑固体表面吸附脱附示意图(上)和程序设计图(下)

如气体分子吸附脱附过程的程序设计图(图1)所示，气体分子以吸附常数k1或k2随机地吸附到格点的最上层，当吸附发生时N(x,y)加1；同样地，格点上气体分子的最上层分子以脱附常数k-1或k-2随机地脱附，当脱附发生时N(x,y)减1。当吸附-脱附达平衡后，单位面积的气体吸附量Na达到动态平衡。吸附时，N(x,y) = 0表示表面层吸附，N(x,y) ＞ 0表示气体层吸附；同理，脱附时，N(x,y) = 1表示从表面脱附，N(x,y) ＞ 1表示从气体层脱附。

饱和蒸气压p*值取决于气体分子凝聚的吸附常数k2和气体分子的脱附常数k−2。模拟过程中我们不计算p*，而是计算约化压强p/p*。根据BET理论，吸附脱附达到平衡时，第i层吸附分子数θi是第i− 1层吸附分子数θi-1的p/p*倍，即θi/θi-1=p/p*。因此模拟中，我们通过计算θ2/θ1和θ3/θ2的平均值得到p/p*= (＜θ2/θ1＞ + ＜θ3/θ2＞)/2。

计算机模拟程序流程如图2所示。模拟程序采用Python语言编写，方便学生学习和修改。吸附过程可以调用提前编译好的Fortran可执行程序，以便更快完成模拟。

图2 计算机模拟流程示意图

1.2 模拟结果和讨论

吸附等温线的形状与吸附热和凝聚热相关，不同体系可通过调节吸附常数和脱附常数k1、k−1、k2和k−2实现。我们分别模拟了三类吸附等温线：(1) 只存在单分子层化学吸附(qa＞＞qc)；(2) 低压区以单分子层吸附为主(qa＞qc)；(3) 多分子层物理吸附为主(qa＜qc)。k1、k−1、k2和k−2四个参数与吸附热qa、凝聚热qc没有直接关联，为了明显给出三类吸附等温线的差别，本文选择了不同的k1、k−1、k2和k−2进行模拟。

当qa＞＞qc时，体系近似于单分子层吸附(第I类吸附等温线)。我们设置固体表面第一层的吸附和脱附常数分别为k1= 0.9和k−1= 0.05，气体吸附层的吸附和脱附常数为k2=k−2= 0。因为气体分子只有单层吸附，我们无法得到p/p*，所以采用气体分子数密度n表示压强p=n。模拟结果如图3所示，在较低压强p下，单位面积的平衡吸附量Na随压强升高而增加，当压强足够大时，吸附达到饱和，不再随压强上升而增加。模拟结论能很好地拟合成Langmuir单分子层吸附等温线：，其中单位面积的饱和吸附量，吸附常数b= 2.9。饱和吸附量表示97%的固体表面被气体分子覆盖。对于不同性质的固体表面和气体分子，Nam和b值可通过改变k1和k−1进行调节。模拟中选择大的k1值和小的k−1值可以使系统更快地达到吸附饱和。

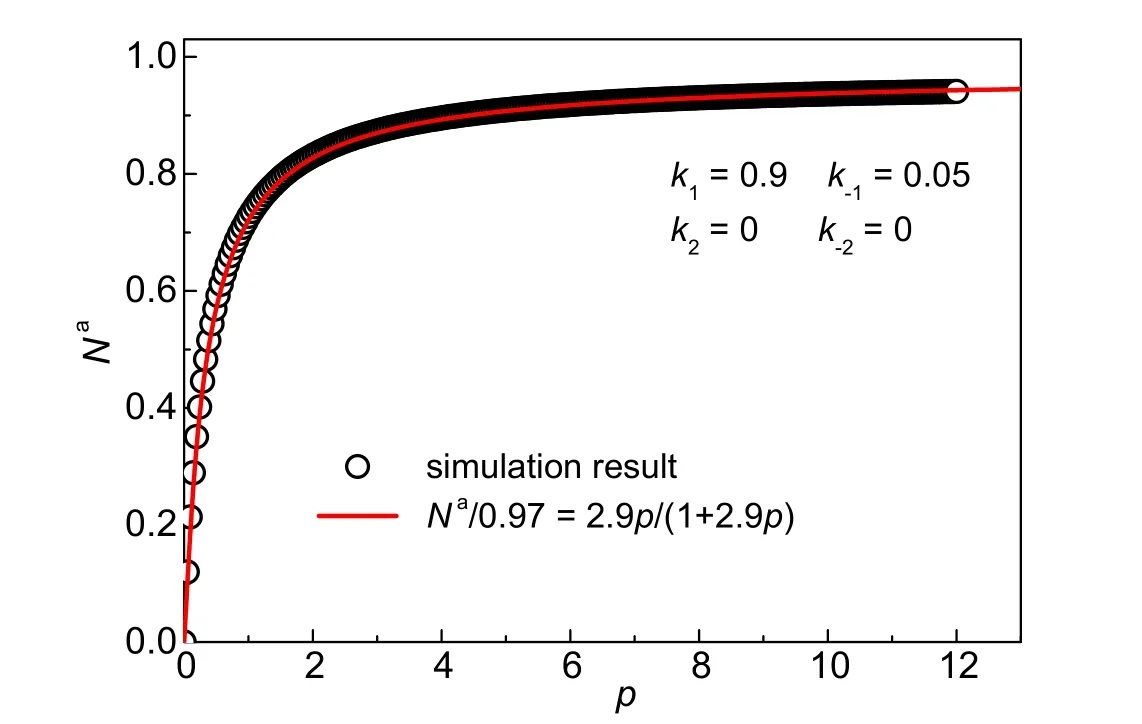
图3 固体表面上单位面积的气体吸附量Na随气体压强p的变化关系

对于qa＞qc的体系，我们固定固体表面层的吸附和脱附常数k1= 0.9和k−1= 0.05，气体吸附层的吸附和脱附常数分别取k2= 0.01和k−2= 0.05。模拟结果见图4(a)，很明显，我们的模拟结果符合第II类吸附等温线，能很好地用二参数BET公式进行拟合：

图4 (a) 气体吸附层的吸附常数k2 = 0.01时模拟得到的第II类吸附等温线；(b) k2不同时，单位面积吸附量Na随压强p的变化

当qa＜qc时，以多分子层物理吸附为主，固体表面层的吸附和脱附常数分别取k1= 0.1和k−1= 0.05，气体吸附层的吸附和脱附常数分别取k2= 0.2和k−2= 0.05。模拟结果(图5(a))能很好地再现第III类吸附等温线，拟合参数和c= 0.5。我们进一步模拟了气体吸附层的脱附常数k−2对吸附的影响，脱附常数k−2增加导致脱附作用增强，在相同压强下气体分子的吸附量减少，结果如图5(b)所示。小的k−2值代表弱脱附，因此小的k−2值有利于观察到第III类吸附等温线。

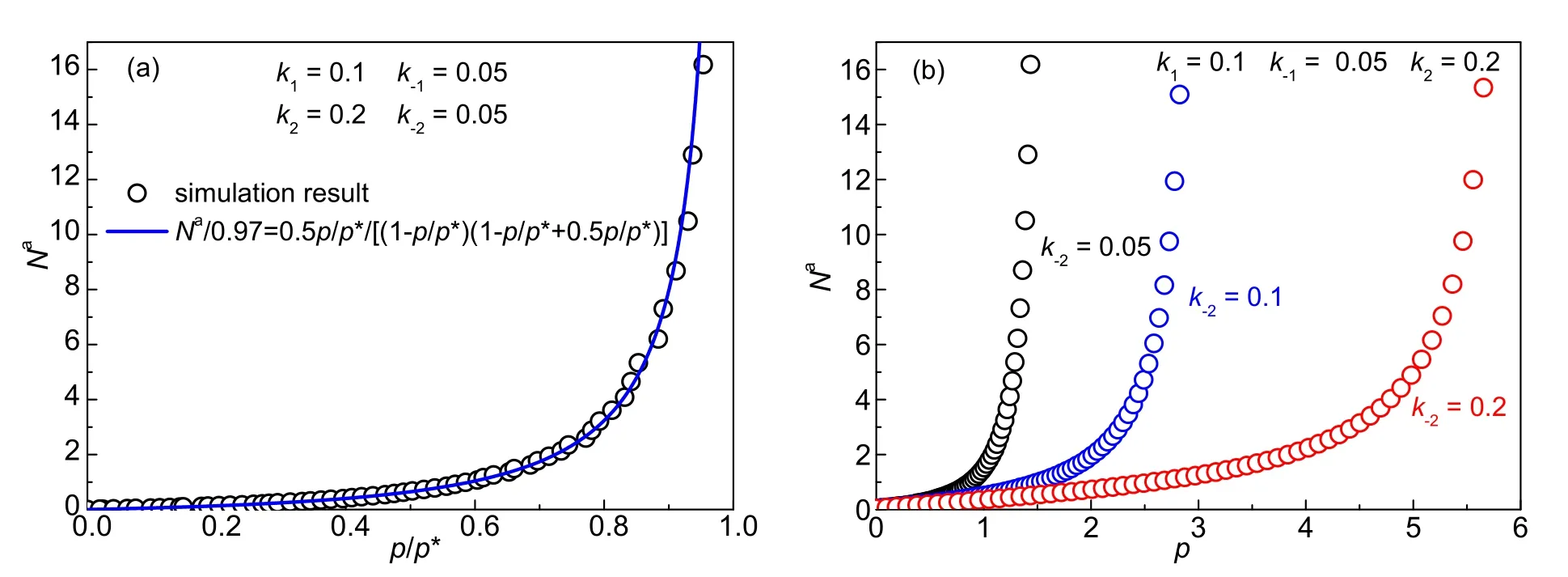
图5 (a) 气体吸附层的脱附常数k−2 = 0.05时模拟得到的吸附等温线；(b) k−2不同时，单位面积吸附量Na随压强p的变化

我们还可以实时跟踪气体分子的吸附动力学过程。以k1= 0.9，k2= 0.01，和k−1=k−2= 0.05的体系(第II类吸附等温线)为例，如图6所示，随着吸附时间延长，吸附量Na快速增加，并达到吸附平衡。平衡吸附量随气体压强增大而增加；吸附达到平衡所需的时间也随气体压强增大而增加。模拟过程中，我们还实现了气体分子在固体表面的吸附过程以及吸附脱附动力学等微观信息的实时可视化，如图7所示的不同压强下的气体实时吸附图能让学生直观看到气体分子在固体表面的吸附机制和吸附脱附动力学，更好地理解各种吸附模型。将计算机模拟穿插到课堂教学中能充分活跃课堂气氛，实现教与学互动，提高教学质量。

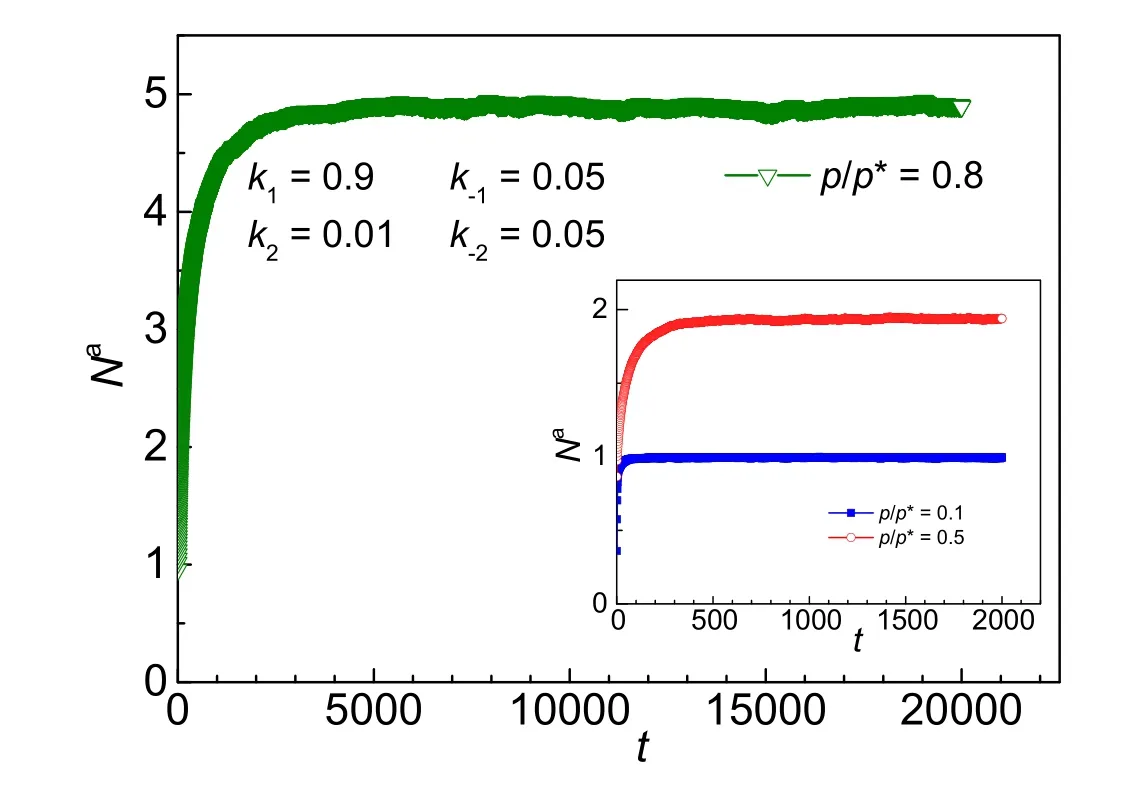
图6 不同压强下气体吸附量随吸附时间的变化过程

图7 不同压强下的气体实时吸附图

2 教学方案

计算机模拟辅助BET吸附理论教学包含课堂演示和课后自学两部分。课堂教学安排1学时，教师按如下方案开展课堂教学：

(1) 介绍气体分子在固体表面吸附的计算机模型、模拟方法、模拟程序的设计流程和参数调节；

(2) 课堂演示程序运行方法和步骤，学生在教室的投影屏幕上能实时观察气体分子在固体表面的吸附过程以及吸附脱附动力学；

(3) 程序运行结果通过Origin软件处理后确定吸附等温线的类型。Origin软件学生已在“化学信息学”课程中学过。

由于课堂教学时间有限，我们将模拟程序源代码、程序说明和参数调节方法分享到班级QQ学习群，方便学生在课后自学练习。Python程序简单易学，非计算机专业的学生也能很快掌握和使用。Python程序可以实时输出气体吸附量Na随吸附时间的变化过程、吸附等温线，以及气体实时吸附图等内容。学生在课后可以方便地调节参数和修改程序，激发学生的求知欲和学习积极性。如前所述，BET公式假设了固体表面均匀、表面各吸附位点的吸附热相等、多层吸附时每层凝聚热都相同等条件，因此，实验发现BET公式只在p/p*= 0.05–0.35范围内适用[13]。但模拟可以遵守这些BET假设，因此可以在更大的压强范围内适用，如图4(a)和5(a)所示。学生还可以通过修改程序，模拟更接近实际的体系，如粗糙固体表面、吸附位点不均匀的固体表面以及被吸附的同层气体分子之间存在相互作用等，模拟结果在QQ学习群进行交流，从而开阔学生视野，激发学生的科研兴趣。

该教学方案率先在2020级应用化学专业试行，学生反响积极，普遍反映有助于加深理解BET吸附理论，很多同学希望物理化学的其他抽象难懂的知识点以及涉及复杂数学推导的公式也能开展类似的计算机模拟辅助教学。

3 结语

物理化学课程教学中有很多看不见摸不着、很抽象但又具广泛应用背景的知识点，通过把计算机模拟技术引入到物理化学课堂教学中，教师能将抽象概念和理论表现为定量数据和直观图像，激发学生的求知欲；还能充分活跃课堂氛围，提升教学趣味性，实现教与学互动。这种将理论和计算机模拟相结合的教学方法丰富了现代教学方法，能激发学生的学习主动性和科研兴趣，提高教学质量，为培养学生的创新能力和建立正确的科学研究方法奠定基础。