一道求三角形正切值问题的解法探究

梁志佩 (邮编:671003)

云南省大理大学教师教育学院

黄丽婷 (邮编:515400)

广东省揭西县第一中学

在高考中,常常遇到求三角形正切值的题目,那么如何快速求解三角形的正切值,这就要求学生熟练掌握三角形边与角关系的相互转化,在数形结合基础上,运用正弦定理、余弦定理、三角形面积公式等综合计算解答,下面以2023年新高考II卷17题第一问为例,通过多种视角求解,并进行变式推广,提升学生的分析、解决问题的能力.

1 真题再现

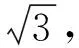
题目分析该题已知△ABC的面积、AD长,关键要利用三角形的面积公式求出CD长或CD边上的高;可以运用余弦定理求出cosB,再计算sinB,最后得到tanB;此外也可以考虑构造出关于∠B的直角三角形,一步到位求出tanB;当然这道题给了边BC中点,也可以考虑构造△ABC的中位线,构造出∠B的同位角,结合初高中的三角形知识,求出tanB,下面为大家展示各种思路的解法.

思路1余弦定理

图1

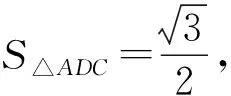
评析这种方法体现了方程的思想,在△ABD中用了两次余弦定理即可求解,即在余弦定理公式中知三求一,计算出cosB,再利用同角三角函数的基本关系求出sinB,最终求解出tanB,较为常规的方法,学生不难想到.

思路2正弦定理

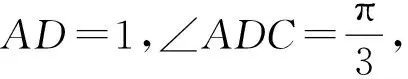
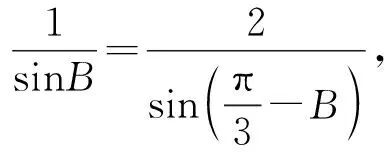
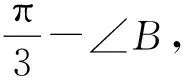
思路3巧用“1”“乘”变“除”

思路4构造平行线(中位线)

图2

评析该解法构造了边AB的平行线DE,将求解∠B转化为∠CDE(因为已知条件均为△ADC的边和角),把所求问题向已知条件靠拢,快速求解,在解三角形题目中,如果涉及角度的求解,可以优先考虑构造平行线或者中位线.

思路5外接圆

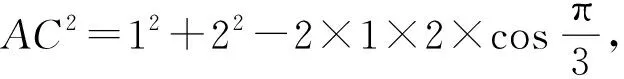
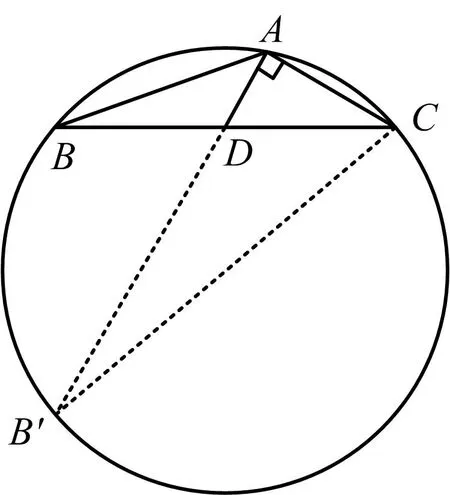
图3

评析该方法作出三角形△ABC的外接圆,利用同弧所对的圆周角相等,将∠B等量替换为∠B′,再利用三角形相似,求出B′D,最后在直角三角形△AB′C,直接求解出tanB′,在三角形某条边为直角边时可以考虑外接圆方法,求正切值.

思路6作某边上的高,求正切值

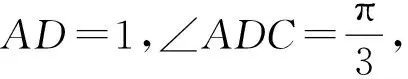
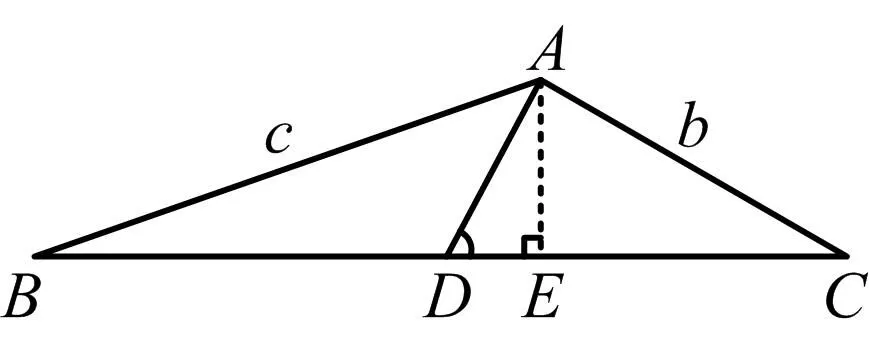
图4

点评这一方法短小精悍,极大简化了计算量,需要同学们发散思维,通过三角形的面积联想到三角形的高,构造直角三角形,利用含有一个角是60°的直角三角形分别求出AE和DE长度,再利用锐角三角函数求解出tanB.该方法是一种通性通法,对于D是BC的k等分点,依然适用.

另解如图5所示,利用作高的思路,我们也可以过点D作AB的垂线,垂足为F,在Rt△BDF求tanB,过程与法6类似,这里不再赘述.

图5

思路7平面向量法

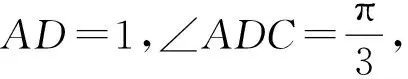
评析向量架起了代数与几何的沟通桥梁,该方法引入了平面向量来解三角形,可见向量是解决三角形问题非常重要的工具,当我们引入向量往往会给我们“山重水复疑无路,柳暗花明又一村”的感觉,这也是教材使用向量法推导余弦定理的重要原因.

2 变式迁移

(2023全国乙卷)在△ABC中,已知∠BAC=120°,AB=2,AC=1

(1)求sin∠ABC;

(2)若D为BC上一点,且∠BAD=90°,△ADC的面积;

(3)在(2)的条件下求tanC.

分析(1)常规方法:由题意先求出BC长度,再在△ABC中用余弦定理求出cosB,再求出sinB,但这里可以使用本文的思路3(巧用“1”“乘”变“除”)解答更加简便一点,请看下面过程:

解(1):如图6

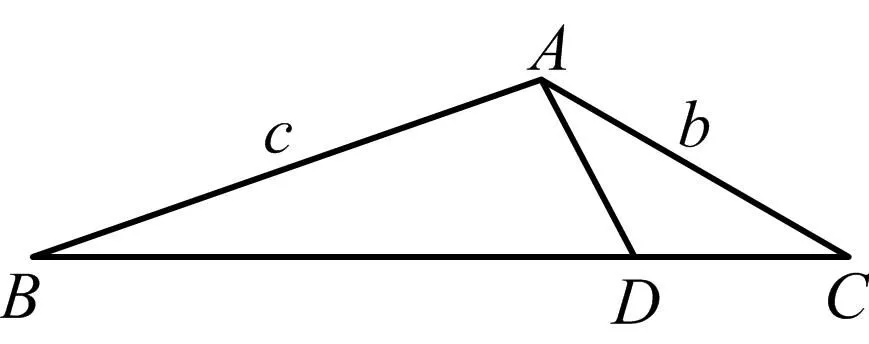
图6

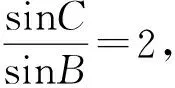
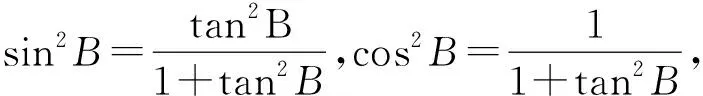
(2)采用本文的思路4(作平行线),详见下解法

图7

评析此方法计算量小,当题目给出D是几等分点时,使用该方法最佳.

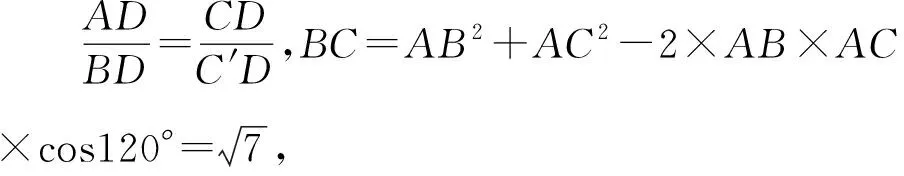
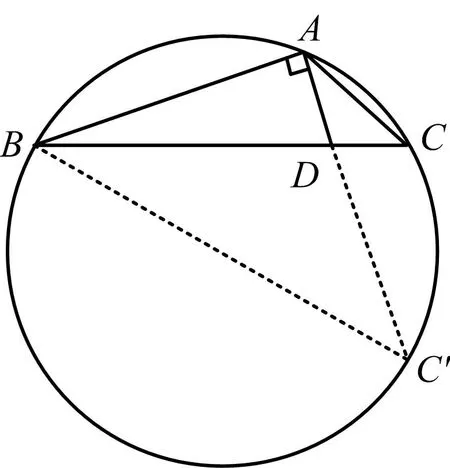
图8

评析此方法利用已知的直角,将tanC放到△ABC′中求解,较为快捷,是一种不寻常的简便方法.

3 解后反思

通过上述的解法,可以看到求解三角形正切值的方法灵活多样,在解题的过程中,要分析已知条件的特点,思考解答的路径有哪些,在解答中可以通过与初中所学知识、公式定理结合,比如直角三角形的三角函数、构造平行线同位角相等、同弦所对的圆周角相等;进而选择简便、适合自己的方法,提高解题速度;在平时的做题过程,同学们可以尝试思考不同的解题方法,培养自己的发散思维.