带时间窗的中心站多车程集卡调度优化研究

李琦，魏玉光

(北京交通大学，交通运输学院，北京 100044)

0 引言

铁路集装箱中心站是铁路集装箱运输的关键场所，也是公铁联运的重要节点。中心站的集卡承担着公铁联运箱流在中心站与货源地间的集疏任务，其集疏效率直接影响整个公铁联运集疏系统的作业效率。多车程集卡集疏调度旨在确定集装箱的集疏方案和集卡的调度方案，以最小化综合运营成本，并提高中心站的集疏效率与能力。

带时间窗的中心站多车程集卡调度问题是车辆路径优化问题的拓展，是带时间窗的取送货问题(VRPSPDTW)与多行程问题(MTVRP)相结合的综合性问题。国内外学者对这两类问题展开了广泛的研究。Mahmoudi等[1]提出前向动态规划算法，用于解决单车VRPSPDTW，利用拉格朗日松弛法，将多车路线问题分解为多个单车路线子问题。Wu等[2]利用带有破坏和修复策略的蚁群算法求解VRPPDTW。Shi等[3]采用两阶段算法来解决VRPSPDTW，第1阶段提出基于学习目标函数的改进变量邻域搜索方法，第2阶段设计了基于双结构的禁忌搜索算法，以优化车辆数量与走行距离。王超等[4]以最小化运输距离和车辆数为目标，设计离散布谷鸟算法，使用2-opt法、shift/swap法改进路径的搜索过程。于江霞等[5]设计遗传算法求解基于客户分类的配送路径优化模型。Francois等[6]构建以车辆总行驶时间最小为目标的多行程车辆路径模型，并设计带有多行程算子的自适应大邻域算法。Pan等[7]研究了城市物流配送中，时变路网下的多行程车辆路径问题，并采用混合元启发式算法进行求解。彭勇等[8]设计混合遗传算法用于求解基于交换箱甩挂的路径优化问题。

上述学者所研究的问题具有车辆容量大、时间窗较为宽松的特点，并使用启发式算法来确定最优成本及车辆使用数量。本文与前述研究的不同之处在于：首先，由于公铁联运集疏系统注重集装箱集疏作业的时效性，需要考虑公路与铁路的衔接，故采用由列车到发时刻确定的混合时间窗作为模型的时间约束，以确保集卡能够按时完成集装箱的集疏任务；其次，与一般配送车辆不同，集卡通常只能装载一个集装箱，因此，采用多车程作业模式进行集卡调度；最后，通过启发式算法求解出的集卡调度方案无法保证集卡作业时间的均衡性，需要解决集卡作业时间不均衡的问题。

对集卡调度优化问题的研究集中在港站内的集卡调度和集卡预约分配两个方面，对中心站与收(发)货地间集卡调度问题的研究相对较少。He等[9]研究了码头外集卡的任务分配问题，以任务均衡和集卡到达均衡为优化目标，建立了外集卡调度模型。Jiang等[10]研究了多式联运枢纽节点的箱流分配及集卡调度问题，采用分支定价法求解模型。Nossack等[11]在集卡调度优化模型中考虑了硬时间窗约束，采用两阶段法解决多式联运港站的外集卡调度问题。Hong等[12]研究了港站内无人集卡的配置与调度问题。靳志宏等[13]针对甩箱模式下多箱型任务组合的集卡调度问题，在考虑箱位变化的基础上，以最小化集卡综合调度成本为目标，设计了基于不可行弧过滤策略的蚁群算法。许波栀等[14]研究早晚高峰拥堵情况下的集卡预约调度问题，利用自适应量子遗传算法确定集卡数量及到港时间窗。

综上所述，为解决铁路集装箱中心站与周边货源地间的集卡调度问题，本文综合考虑中心站箱流集疏和集卡调度的特点，将车辆路径理论应用于公铁联运集装箱的集疏问题。同时引入多车程的概念，即集卡能够在完成当前集疏任务后，继续从中心站出发执行其余集疏任务。此外，通过列车到发时刻来确定集装箱的集疏时间窗，以体现集卡与班列在中心站集疏系统中的时间关系。在研究多车程集卡调度的基础上，进一步探讨集卡的车程分配问题。

1 问题描述

公铁联运主要包括“集”“疏”“运”这3个过程，如图1所示，其中a，b，c为货源地节点，m为中心站节点。“集”是通过公路运输将公铁联运集装箱送达中心站，“疏”是通过公路运输将货物从中心站送达收货地，“运”是将中心站的货物转运至其他集装箱中心站或铁路车站。

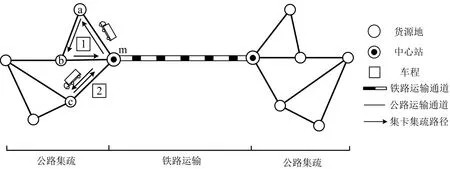
图1 集疏运组织模式Fig.1 Collection and distribution organization model

在公铁联运的3个作业环节中，集装箱的集疏作业主要在公路运输系统中完成，运输作业主要在铁路运输系统中完成。为体现公铁联运集装箱集疏运作业的协调性，本文利用中心站的列车到发时刻来确定集装箱的集疏时间窗。由于中心站内的列车针对同一货源地可能具有不同的集疏箱流任务，导致集装箱的集疏时间窗存在一定的差异。因此，采用虚拟节点拆分的方法，将货源地节点拆分成多个虚拟节点，如图2所示。虚拟节点数量等于原节点的集疏箱量。虚拟节点与原节点具有相同的地理位置，但集装箱的集疏性质及时间窗存在差异。

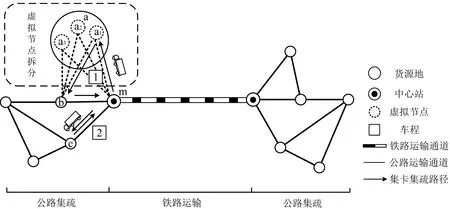
图2 虚拟节点拆分Fig.2 Virtual node splitting

集卡的集疏作业主要有单车程和多车程两种模式。所谓车程，是指集卡从中心站出发，并最终返回中心站的作业行程。图2 包含两个车程，车程1 为m-a1-b-m，车程2 为m-c-m。以图2 为例，单车程作业模式要求每辆集卡仅执行一项车程任务，因此需要两辆集卡各完成一项车程任务；而多车程作业模式允许每辆集卡执行多项无时间冲突的车程任务，即一辆集卡可以连续完成这两项车程任务。这表明采用单车程作业模式能够更快地完成中心站的集疏任务，但会大幅增加集卡的使用数量，从而增加集卡的调度成本。因此，本文基于多车程的概念，对公铁联运背景下的中心站多车程集卡集疏调度优化问题展开研究。

2 模型构建

2.1 模型假设

基本假设如下：

(1)集卡是同质的，集卡1次最多装载1个40 ft集装箱；

(2)允许集卡重复使用；

(3)节点间的路径为双向连通路径，节点优先级相同；

(4)集装箱箱型一致；

(5)中心站的装卸作业能力充足，不存在集卡在装卸线上等待的情况。

2.2 符号说明

模型所涉及的符号及说明如表1所示。

表1 集合、参数及变量说明Table 1 Set,parameter,and variable descriptions

在时间窗的设定方面，采用随机设定的方法难以满足公铁联运作业过程中对集装箱集疏时间的要求。因此，本文根据列车的到发时刻确定集装箱的集疏时间窗。其中，列车到发时间窗设置为[A,D]，A为列车到达时刻，D为列车出发时刻，则集装箱的疏运时间窗为[A+dOjv+tc,D+dOjv+tc]，集运时间窗为[A-dOj′c,D-dOj′c] 。

2.3 带时间窗的中心站多车程集卡集疏调度模型

(1)目标函数

模型目标为最小化集卡的调度成本。调度成本由集卡走行成本，与运输距离无关的集卡固定成本和时间惩罚成本组成。通过引入惩罚成本来体现允许集卡提前到达节点的软时间窗。

(2)约束条件

模型的约束条件包括3个方面：集卡作业接续关系、运输需求与集卡容量、作业时间关系的相关约束。

①集卡作业接续关系约束

式(2)和式(3)表示每个集卡车程中的节点都有唯一的前序节点和后序节点，且每个节点仅被访问一次；式(4)表示集卡不存在从节点出发又返回该节点的情况；式(5)和式(6)表示集卡从中心站出发，执行完当前车程任务后均需返回中心站；式(7)表示集卡车程中节点的连续性。

②运输需求与集卡容量约束

式中：|R|为车程数；Q为集卡容量；M为较大的正数。

式(8)和式(9)表示集疏作业能力应满足集疏需求；式(10)和式(11)表示节点的集运量与疏运量平衡约束，确保各节点的集疏任务都能被满足；式(12)和式(13)表示每辆集卡在执行车程任务时，每个节点的装卸箱量均不超过集卡容量；式(14)表示集卡在完成当前节点集疏任务后的装载量；式(15)表示集卡仅访问有集疏需求的节点。

③作业时间关系约束

式(16)表示集卡到达各节点的时间等于集卡到达前序节点的时间、装卸作业时间和节点间走行时间这三者之和；式(17)表示集卡车程在时间上的接续关系；式(18)表示不允许集卡晚于规定的时间到达节点，这与目标函数中惩罚成本所代表的软时间窗相结合，构成本文的混合时间窗；式(19)表示集卡在节点间的走行时间。

2.4 多车程分配优化模型

(1)目标函数

带时间窗的中心站多车程集卡集疏调度模型可以确定最佳集卡数量、车程集合及调度方案，但无法保证每辆集卡作业时间的均衡。因此，本文以最小化集卡间作业时间差值为目标，构建多车程分配优化模型为

(2)约束条件

模型的约束条件包括两个方面：任务接续关系和集卡走行时间的相关约束。

①任务接续关系约束

式(21)表示每个车程只能由一辆集卡提供服务；式(22)和式(23)引入虚拟车程“0”，以确保每辆集卡都有唯一的起止车程；式(24)表示当前车程的前后续车程必须由同一辆集卡完成。

②集卡走行时间约束

式(25)表示每辆集卡的总作业时间；式(26)表示集卡作业时间不超过规定的最大作业时间，规定Tmax=8；式(27)表示集卡车程的开始时刻，若车程为集卡的起始车程，则开始时刻为该车程的最早开始时刻，否则为前序车程的结束时刻；式(28)表示车程时间窗，集卡需要在规定的时间范围内完成当前车程任务。

对模型的目标函数及非线性约束进行线性化处理。通过引入辅助变量fmax，fmin将式(20)线性化表示为

引入0-1变量αk，将式(30)线性化表示为

式(31)同理。

3 求解方法

带时间窗的中心站多车程集卡调度优化问题的求解主要分为两部分，如图3 所示。首先，采用改进的遗传算法求解中心站集疏调度模型，旨在获取最佳的集卡调度成本及方案。其次，为提高集卡间调度作业的均衡性，以调度模型得到的集卡数量及车程集合为输入，借助Gurobi优化器确定作业时间更为均衡的集卡调度方案。考虑到车辆路径问题的特点和遗传算法在全局搜索中的优势，本文在遗传算法中引入模拟退火算法的Metropolis接受准则，通过改进的遗传算法求解中心站集卡集疏调度模型，关键设计如下。

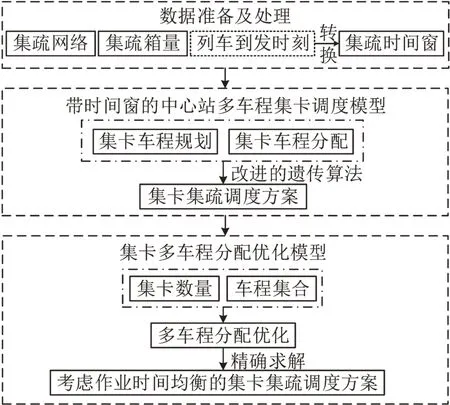
图3 求解流程图Fig.3 Flowchart of solution

(1)种群初始化

种群的初始化过程实际上是车程的规划过程。采用虚拟节点拆分法将货源地节点拆分成集疏任务节点，将虚拟节点随机排列组成染色体的基因。根据集卡容量、时间窗等约束条件，利用中心站节点分割序列得到车程集合，如图4所示。适应度函数为F=1Z。

图4 分割过程Fig.4 Segmentation process

(2)车程时间窗

根据集装箱的集疏时间及装卸作业时间来确定车程的最早开始时刻、最晚开始时刻及持续时间。

式(34)表示集卡执行车程任务的最晚开始时刻，其中，集合N由0～n组成，表示车程的节点。从n-1 逆推出车程中各节点的最晚出发时刻ltrr,iip，从而得到车程的最晚开始时刻ltrrip。式(35)表示集卡执行车程任务的最早开始时刻。式(36)表示车程的持续时间。

(3)车程分配策略

通过车程分配策略确定集卡的数量及行驶计划，步骤如下：

Step 1 确定车程集合R。

Step 2 计算集合R中车程的开始时间窗和持续时间。

Step 3 若集合R非空，则执行Step 4；否则，执行Step 5。

Step 4 按照车程的最早开始时刻升序排列，遍历集合R，依次将车程插入到集卡作业计划Pk中。假设集卡作业的结束时刻为，若则将车程r分配到Pk中，更新集卡作业的结束时刻为，从集合R中删除车程r，跳转至Step 3；若，则将车程r分配到Pk中，更新集卡作业的结束时刻为，从集合R中删除车程r，跳转至Step 3；若，则车程无法插入Pk中，重复Step 4，直至遍历完集合R，选取新的集卡执行新一轮的车程分配过程。

Step 5 返回集卡作业计划及起止时间。

(4)选择过程

传统的轮盘赌选择法可能会淘汰优良个体。本文设计改进的轮盘赌选择法，以保留优良个体。首先，将染色体{x1,x2,…,xn} 按照适应度的大小降序排列，得到新的染色体序列{y1,y2,…,yn} 。其次，计算适应度总和，个体选择概率，其 中，i∈{1,2,…,n}，累计适应度，x为染色体序号。随后在每轮选择中生成n个[0,1]区间内的随机数{r1,r2,…,rn}，选择随机数分布最多的个体作为子代，如图5所示。

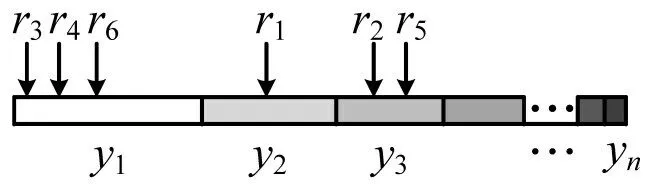
图5 随机数分布Fig.5 Random number distribution

(5)搜索策略

当父代染色体相同时，传统的部分匹配交叉会产生基因相同的子代，影响算法的搜索能力与搜索范围。因此，本文通过设计改进的交叉算子增强种群的多样性。首先，设定4个随机数来确定染色体中的两个待交叉区域；其次，将其置于对方染色体前端并消除重复元素，最终得到交叉后的子代染色体，如图6所示。

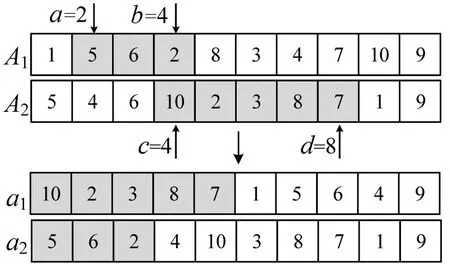
图6 交叉操作Fig.6 Cross-operation

为提高搜索能力，在交叉过程中嵌入Metropolis原则，利用退火寻优的方法，在保留优良解的同时，以一定概率接受劣质解，以此扰动搜索过程。具体步骤如下：

Step 1 设定初始温度T与衰减系数α。

Step 2 模拟退火操作，对染色体A1，A2执行交叉操作，得到子代染色体a1，a2，计算适应度FAi,Fai。若Fai>FAi，i=1,2，则子代取代父代染色体，否则以概率P接受子代染色体。

变异过程采用Swap算子来交换路径间的单个节点，如图7 所示。采用贪婪搜索策略，保留变异结果中适应度最大的个体。

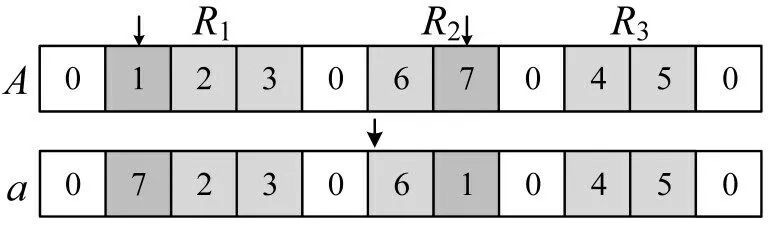
图7 Swap算子操作Fig.7 Swap operator operation

4 算例分析

4.1 数据准备

本文以郑州铁路集装箱中心站为配送中心，构建腹地集装箱集疏网络，集疏网络相关信息如表2所示。设计不同规模算例验证模型的有效性和稳定性，算例参数如表3 所示。实验在i7 处理器，2.6 GHz 的计算机上运行，使用MATLAB2020a 编写程序。种群规模设置为300，迭代次数为500，交叉概率为0.95，变异概率为0.05，初始温度为100 ℃，衰减系数为0.99。

表2 集疏网络节点信息Table 2 Collection and distribution network node information

表3 相关参数Table 3 Relevant parameters

4.2 小规模算例

设置小规模算例(集疏箱量为20、30、40，列车数为1、2、3)比较多车程作业模式与单车程作业模式在中心站集卡调度过程中的不同，利用本文的算法将每个算例独立运行10 次，得到不同模式下的集卡调度总成本，结果如表4 所示。其中，T1、T2分别为多车程作业模式及单车程作业模式下的中心站总体集疏作业时间，即最后一项集疏任务的完成时间与最早一项集疏任务的开始时间之差。

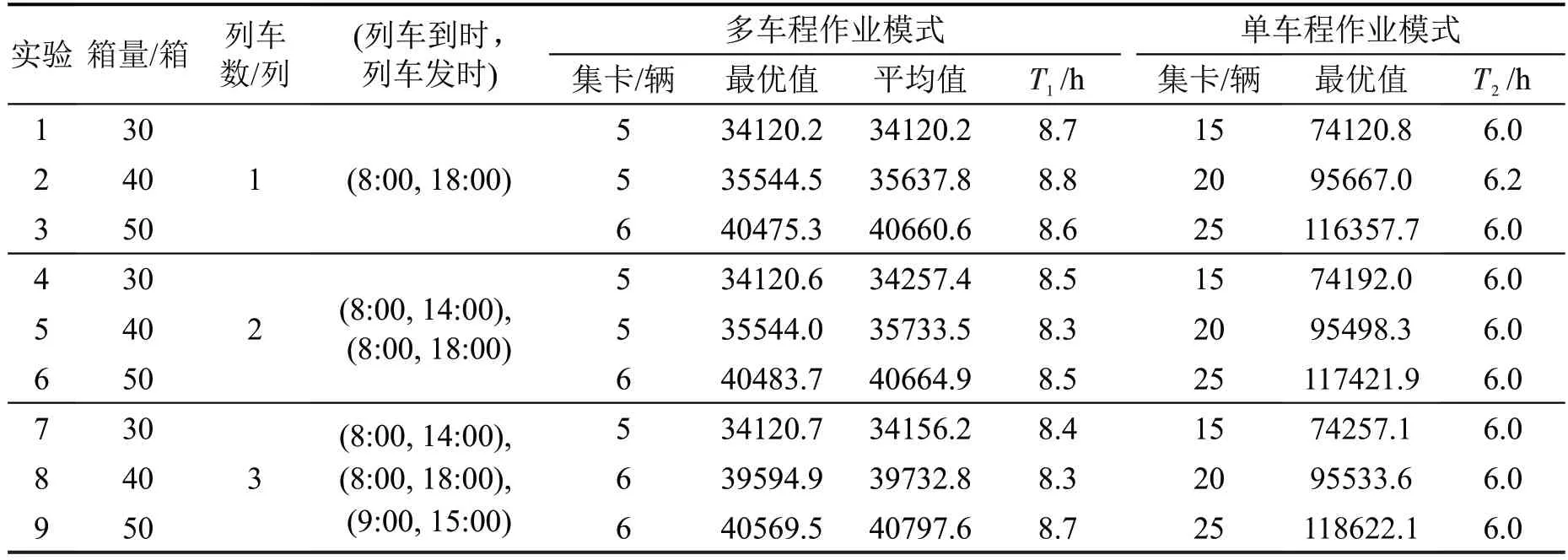
表4 两种车程模式的求解结果Table 4 Result of two transportation modes

由表4可知，多车程作业模式的集卡调度成本低于单车程作业模式的集卡调度成本，平均减少了60.31%。相较于单车程作业模式，多车程作业模式能够有效减少集卡的使用数量，进而降低集卡调度成本。比较不同模式下中心站的总作业时间发现，单车程作业模式能够在6 h 左右完成所有集疏任务，比多车程作业模式下的总体作业完成时间平均缩短了29.4%，说明单车程作业模式能够更快地完成集疏任务，缩短中心站的总体作业时间。虽然多车程模式下中心站总作业时间相对较长，但使用的集卡数量远少于单车程模式，随着箱流规模增大，两种模式下的集卡数量差距也随之增大。通过比较实验2，实验5 和实验8 发现，实验8 的集卡数量增加了1 辆。这是由于集装箱集疏时间窗受班列到发时间窗的影响，随着班列数量的增加，集装箱具有更加复杂的集疏时间窗，限制了集卡的作业顺序，导致集卡数量增加。

4.3 大规模算例

为进一步验证集卡调度模型的有效性及多车程分配优化模型的效果，设置大规模算例(集疏箱量为90、120，列车数为4、5、6)，利用本文算法求解多车程作业模式下的集卡调度模型，借助Gurobi优化器求解车程分配优化模型，实验结果如表5 所示，其中，ΔT1为优化前的集卡作业时间差，ΔT2为优化后的集卡作业时间差。

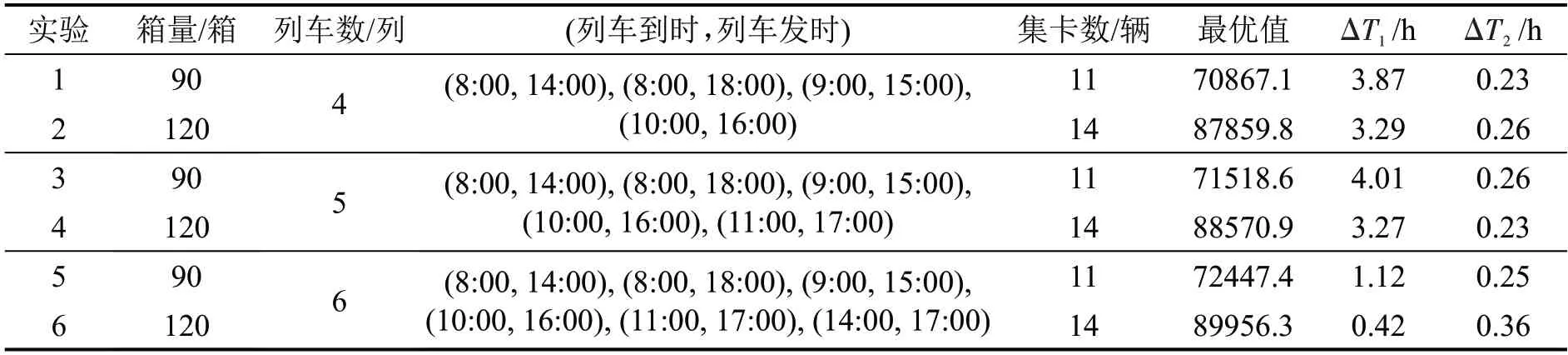
表5 多车程作业模式求解结果Table 5 Result of multi-trip operation scheduling

由表5可知，增大箱流规模会增加集卡的使用数量及调度成本，而班列数量对集卡使用数量的影响并不明显。班列数量直接影响集装箱的集疏时间窗，进而对箱流集疏次序及集卡走行路径产生影响，从而改变集卡运输距离成本。实验6的迭代曲线如图8 所示，迭代约350 次得到最优解并进入收敛状态。此外，通过对集卡车程的优化，集卡作业时间最大差值减少了14.3%以上，这表明多车程分配优化模型在均衡集卡作业时间方面具有一定的效果。

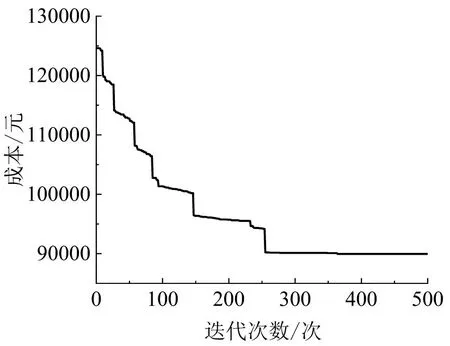
图8 实验6迭代曲线Fig.8 Iterative curve of experiment 6

考虑时间均衡的箱流集疏方案及集卡调度计划如表6所示。结合表6和图9展现的优化前后集卡作业时间可以看出，优化后的集卡作业时间更为均衡，作业时间差值较优化前降低了0.06 h。集卡8承担2项车程任务，作业时间为7.69 h，集卡10承担6项车程任务，作业时间为7.68 h，尽管集卡间承担的车程任务数量不同，但优化模型保证了集卡作业时间的均衡。这表明多车程分配优化模型可以在满足作业要求的前提下，调整集卡的车程分配方案，缩短各集卡作业时间的差距，以实现多车程集卡作业的均衡。这对于实际站内多列车集疏作业的多车程集卡调度具有一定的优化效果。

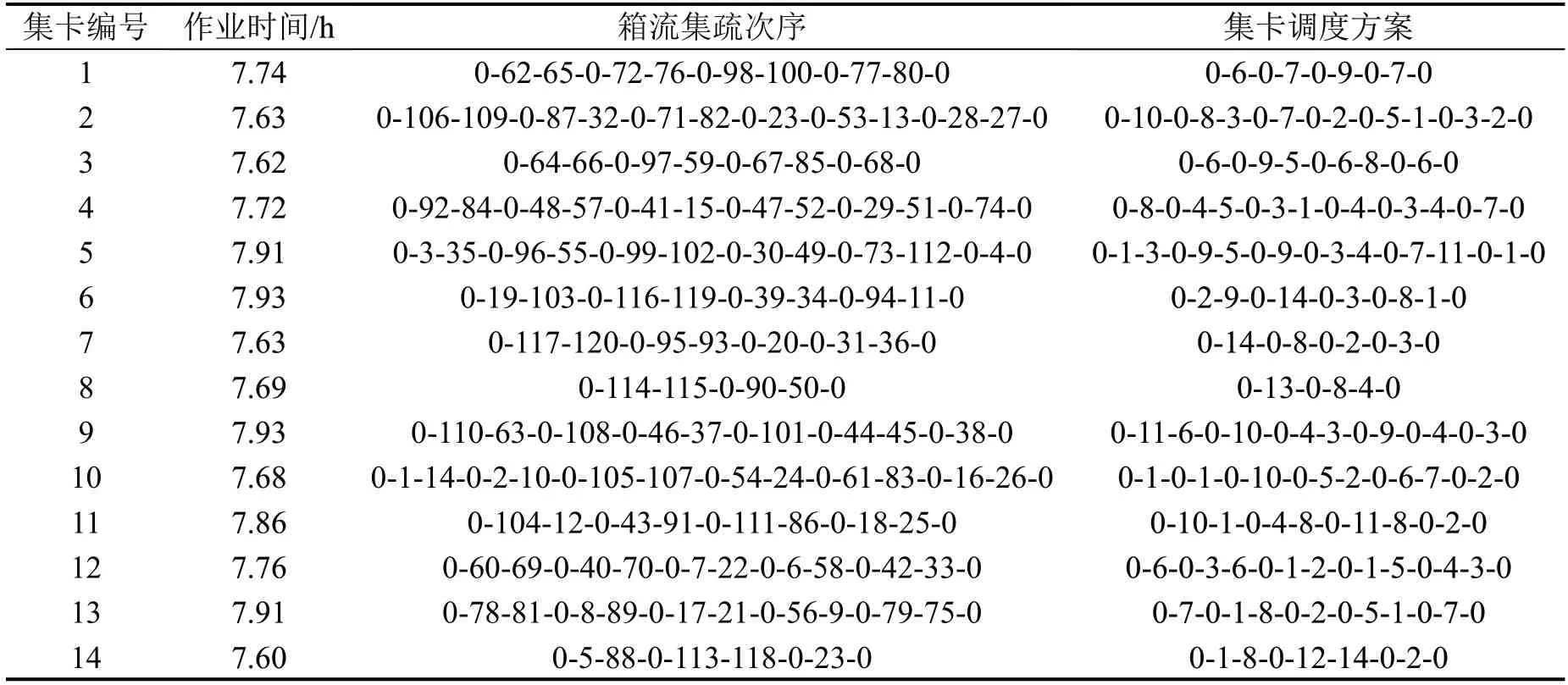
表6 实验6车程分配优化结果Table 6 Optimization results of distance allocation in experiment 6

图9 实验6集卡作业时间对比Fig.9 Comparison of truck operation time in experiment 6

5 结论

本文探讨了公铁联运集装箱集疏领域中带时间窗同时取送货的多车程车辆路径问题，构建了多车程集卡集疏调度优化模型。通过使用中心站列车到发时刻确定集装箱的集疏时间窗，以体现集卡与班列在公铁联运集疏系统中的时间关系。设计改进的遗传算法，并通过算例验证了模型与算法的有效性。此外，构建多车程分配优化模型，以解决集卡车程在时间上分配不均的问题。本文的主要结论如下：

(1)将集卡多车程作业模式引入公铁联运集装箱的集疏问题中，能够有效减少集卡的使用数量，从而降低集卡调度成本。相较于单车程模式，集卡调度成本平均减少60.31%，且随着规模增大，集卡多车程作业的优势越明显。

(2)在多车程集卡集疏调度模型中，将列车到发时刻与集装箱的集疏时间窗相结合，解决了公铁联运系统中的集卡集疏调度问题。通过研究班列数量及箱流规模对集卡调度的影响可以发现，随着集疏箱流规模增大，集卡数量和调度成本也相应增加，而班列数量对集卡数量的影响较小。

(3)本文设计的多车程分配优化模型能够均衡地对作业任务进行分配，进而得出不同箱流规模下的集卡作业时间和作业序列，集卡作业时间最大差值减少了14.3%以上，能够有效解决中心站内实际多列车运营场景下集卡作业时间不均衡的问题。