非单频声场中耦合双泡振动特性研究

李 娜

(宁夏医科大学 医学信息与工程学院，宁夏 银川 750004)

声空化效应及其应用是当前声学、物理学中的一个热门话题.声空化理论研究始于Rayleigh 气泡动力学模型，经过Neppiras 等[1-2]的不断修正，最终得到了单个空化泡的动力学模型，即Rayleighplesset（R-p）方程.但是实际液体中的空化现象是以多泡系统组成的空化云形式存在的，而形成空化云的原因是由于组成空化云的各气泡之间的相互作用力，即次Bjerknes 力[3-4]，双泡是最简单的多泡系统，是研究空化云的切入点[5].Mettin 等[6]计算了强声场中小气泡之间次Bjerknes 力与气泡大小、气泡间距及驱动声压幅值的关系.王德鑫[7]通过考虑双泡之间的辐射压力波，利用Keller-Miksis 方程，计算了不同大小、不同间距、含不同惰性气体的双泡在声空化过程中半径、次Bjerknes 力及双泡内温度的变化规律.马艳等[5]从双气泡耦合振动方程出发研究了强声场中一对初始半径与气泡间距相当的气泡对的耦合振动及气泡之间相互作用的特征.清河美等[8]依据超声场下形成的空化多泡的形状结构，建立了2 种简化的多泡模型，即三泡模型和五泡模型，并利用考虑气泡之间相互作用和液体可压缩性的非线性Keller-Miksis 方程，数值研究了三泡和五泡模型中周围大气泡对中间小气泡空化效应的影响.文献[9]考虑了气泡间次级声辐射影响，得到了表征气泡间相互作用的气泡基本动力学方程以及次Bjerknes 力的表达式，计算分析了气泡平衡半径、声波频率和声压对可能出现的气泡所受到的次Bjerknes 力.Doinikov[10]推导了在弹性介质包围的空腔中填充液体后2 个耦合气泡的非线性动力学方程，并计算分析了气泡之间的耦合振荡.

以上问题的研究过程中均采用单频超声驱动的方式，相关研究表明当用非单频超声驱动单个空化泡时，可以有效提升声空化强度，这对研究空化泡在缩塌时产生更极端的物理条件有重要的意义[11-14].那么如果采用非单频超声驱动，双泡系统将有怎样的规律呢？本文将以双频驱动为例，对非单频驱动下耦合双泡半径、次Bjerknes 力的变化规律进行研究.

1 数学模型

耦合双泡的动力学方程为考虑了气泡之间相互作用的Keller-Miksis 方程，即

式中：R1、R2表示任意时刻球形气泡1、2 的半径，L表示气泡1、2 中心间距，ρ为液体密度，c为液体中声速，ps1、ps2如式（3）、（4）：

式中：p0为液体的静压力，σ为液体的表面张力，v为液体的黏滞系数，pex为外部驱动声压，f为驱动频率，γ为气体绝热压缩系数，R10、R20分别表示气泡1、2 的初始半径，气泡间次Bjerknes 力为[5]

若FB＜0，则气泡1、2 之间相互吸引；若FB＞0，气泡1、2 之间相互排斥.

2 数值计算

本文计算所用参数：液体中的静态压强p0=1.013×105Pa，液体密度ρ=998 kg/m3，液体中的声速c=1 450 m/s，液体表面张力σ=0.072 5 N/m，液体黏滞系数μ=0.001 Pa·s，气体绝热压缩系数γ=1.4.

2.1 单频驱动外部驱动声压pex=p1cos2πft，其中声压幅值p1=1.32p0，驱动频率f=20 kHz，即采用了频率为20 kHz 单频超声驱动方式.令R10=2 μm，R20=5 μm，数值计算结果如图1 所示，图1（a）中横坐标t/T表示时间与驱动周期的比值，纵坐标表示气泡半径，曲线Ⅰ、Ⅱ表示无耦合作用时（即气泡中心间距很大）.计算结果表明气泡1 在31.62 μs时达到最大膨胀半径15.57 μm，最大值为初始值的7.88 倍；气泡2 在34.38 μs 时达到最大膨胀半径45.32 μm，最大值为初始值的9.06 倍.曲线Ⅲ、Ⅳ分别表示气泡1、2 相互耦合时（气泡间距L=0.2 mm），半径在1 个驱动周期内的演化曲线，其中气泡1 在27.47 μs 时达到最大膨胀半径5.40 μm；气泡2 在34.38 μs 时达到最大膨胀半径45.32 μm，其耦合作用时的半径演化曲线与无耦合时半径演化曲线重合，这是由于耦合气泡之间大气泡对小气泡有着较强的抑制作用.图1（b）所示为耦合气泡间次Bjerknes 力在1 个驱动周期内呈现出先吸引、后排斥的振荡变化，其平均值为3.59×10-9N，这表明气泡之间相互排斥.

图1 单频驱动f=20 kHzFig.1 Single frequency f=20 kHz drive

2.2 双频驱动外部驱动声压pex=p1cos2πf1t+p2cos2πf2t=p1cos2πft+p2cos（3×2πft），其中f=20 kHz，即采用了频率f1=20 kHz 与频率f2=60 kHz 的双频驱动.令R10=2 μm，R20=5 μm，p1=1.32p0，p2=0.66p0（p2∶p1=1∶2）.计算结果如图2 所示，气泡1、2 在34.35 μs 时同步膨胀达到最大半径60.97、73.68 μm，半径最大值依次为各自初始值的30.49、14.74 倍；次Bjerknes 力在1 个周期内的平均值为-3.85×10-6N，气泡之间相互吸引，1 个周期时间内次Bjerknes力并未呈现出较强烈的振荡变化.与图1 计算结果比较，双频驱动下耦合双泡半径、次Bjerknes 力的变化规律与单频驱动时不同.

图2 双频驱动f1=20 kHz f2=60 kHzFig.2 Dual frequency drive with f=20 kHz and f=60 kHz respectively

图3 声压幅值之比p2∶p1=0.1∶1Fig.3 Ratio of sound pressure amplitude p2∶p1=0.1∶1

如图4 所示，当驱动声压幅值p2∶p1=0.2∶1一定，p1=1.10p0时气泡1 在28.19 μs 时达到膨胀半径最大值7.60 μm，气泡2 在31.73 μs 时达到最大膨胀半径33.97 μm，气泡间次Bjerknes 力在1 个驱动周期内的变化规律如图7（b）所示，此时气泡间次Bjerknes 力出现激烈的振荡变化，其在1 个周期内的平均值为4.72×10-10N，气泡间相互排斥；当p1=1.25p0时气泡1、2 分别在32.85、33.89 μs 达到最大膨胀半径33.76、52.23 μm，气泡间的次Bjerknes 力在1 个周期内的平均值为-3.14×10-7N，气泡之间相互吸引；当p1=1.32p0时气泡1 在33.43 μs时达到最大膨胀半径42.86 μm，气泡2 在34.84 μs时达到最大膨胀半径60.08 μm，次Bjerknes 力在1个周期内的平均值为-7.63×10-7N.计算结果表明p2∶p1比值一定时，随着p1的增加，气泡1、2 的最大膨胀半径随之增加、膨胀时间逐渐滞后、气泡间次Bjerknes 力的数量级从10-10N 增加到10-7N、次Bjerknes 力由较弱的排斥力逐渐变为较强的吸引力.

图4 声压幅值之比p2∶p1=0.2∶1Fig.4 Ratio of sound pressure amplitude p2∶p1=0.2∶1

图5 声压幅值之比p2∶p1=0.4∶1Fig.5 Ratio of sound pressure amplitude p2∶p1=0.4∶1

图6 声压幅值之比p2∶p1=0.8∶1Fig.6 Ratio of sound pressure amplitude p2∶p1=0.8∶1

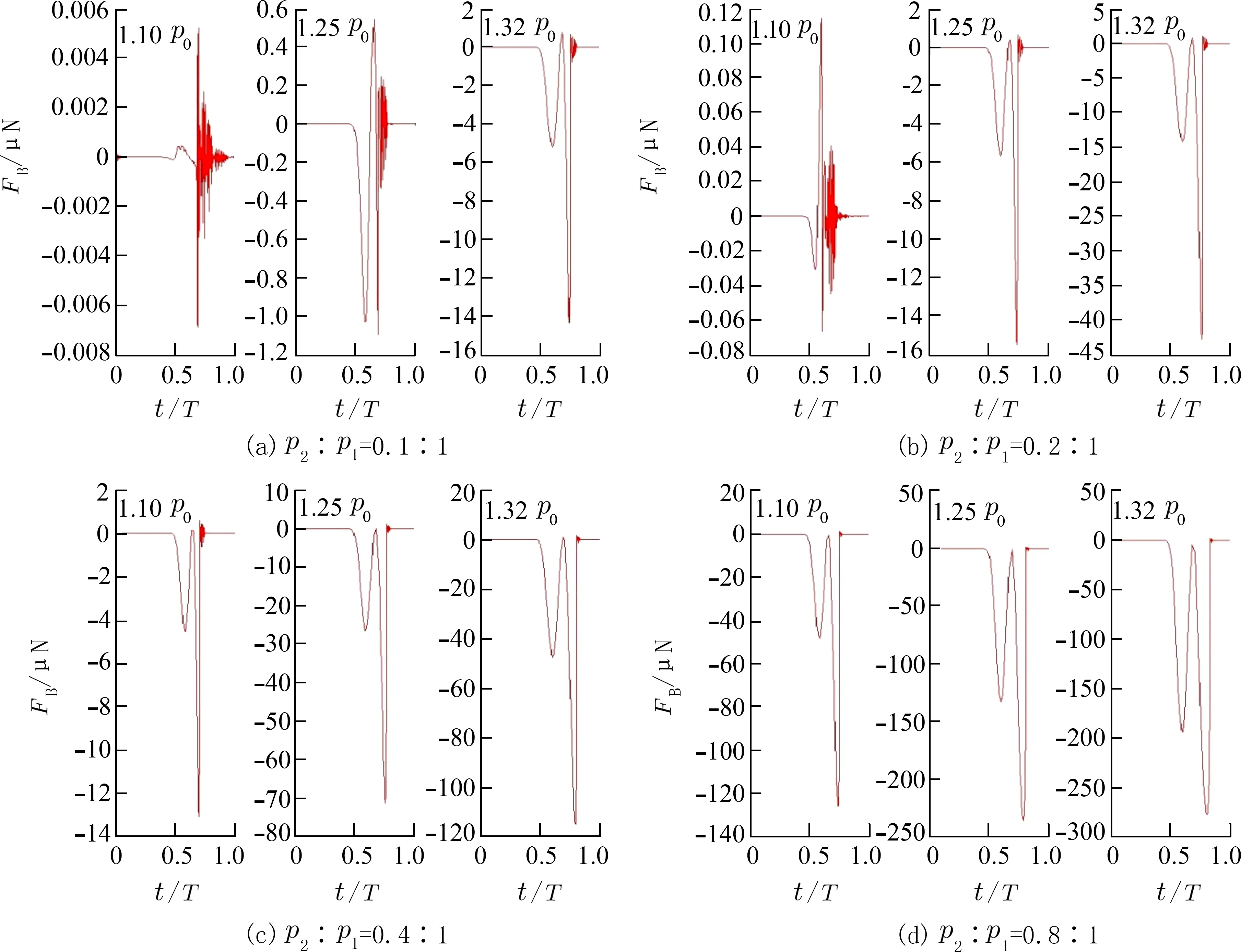
图7 次Bjerknes 力Fig.7 The secondary Bjerknes force

如图3～7 所示，当驱动声压幅值p1=1.25p0一定，p2∶p1比值分别为0.1∶1、0.2∶1、0.4∶1、0.8∶1 时，气泡1 分别在31.43、32.85、32.94、34.14 μs时达到最大膨胀半径20.69、33.76、48.70、67.55 μm；气泡2 分别在33.76、33.89、34.05、34.14 μs 时达到最大膨胀半径45.68、52.23、62.75、78.84 μm；气泡间次Bjerknes 力在1 个周期内的平均值依次为-2.75×10-8、-3.14×10-7、-1.26×10-6、-5.34×10-6N.计算结果表明当驱动声压幅值p1一定时，p2∶p1比值越大，耦合双泡1、2 的最大膨胀半径增大、膨胀时间延迟、气泡间次Bjerknes 力的数量级从10-8增加到10-6、次Bjerknes 力逐渐增强，气泡间引力增强；当驱动声压幅值为p1=1.10p0、p1=1.32p0时，耦合双泡间次Bjerknes、气泡半径变化规律与p1=1.25p0时相似.

如图8 所示，当驱动声压幅值p1=1.32p0，p2=0.66p0，驱动频率f1=40 kHz，f2=120 kHz 时，气泡1、2 分别在16.60、17.20 μs 时达到最大膨胀半径30.81、40.20 μm，次Bjerknes 力在1 个周期内的平均值为-4.26×10-7N.如图9 所示，当驱动声压p1=1.32p0，p2=0.66p0，频率f1=60 kHz，f2=180 kHz 时，气泡1、2 分别在11.25、11.61 μs 时达到最大膨胀半径20.78、28.92 μm，次Bjerknes 力在1 个周期内的平均值为-1.23×10-7N.与图2 计算结果比较可知，驱动频率越高，气泡最大膨胀半径越小，气泡间的次Bjerknes 力也随之减小，这是由于驱动频率越高，气泡生长周期变短，从而使气泡生长受到了抑制.

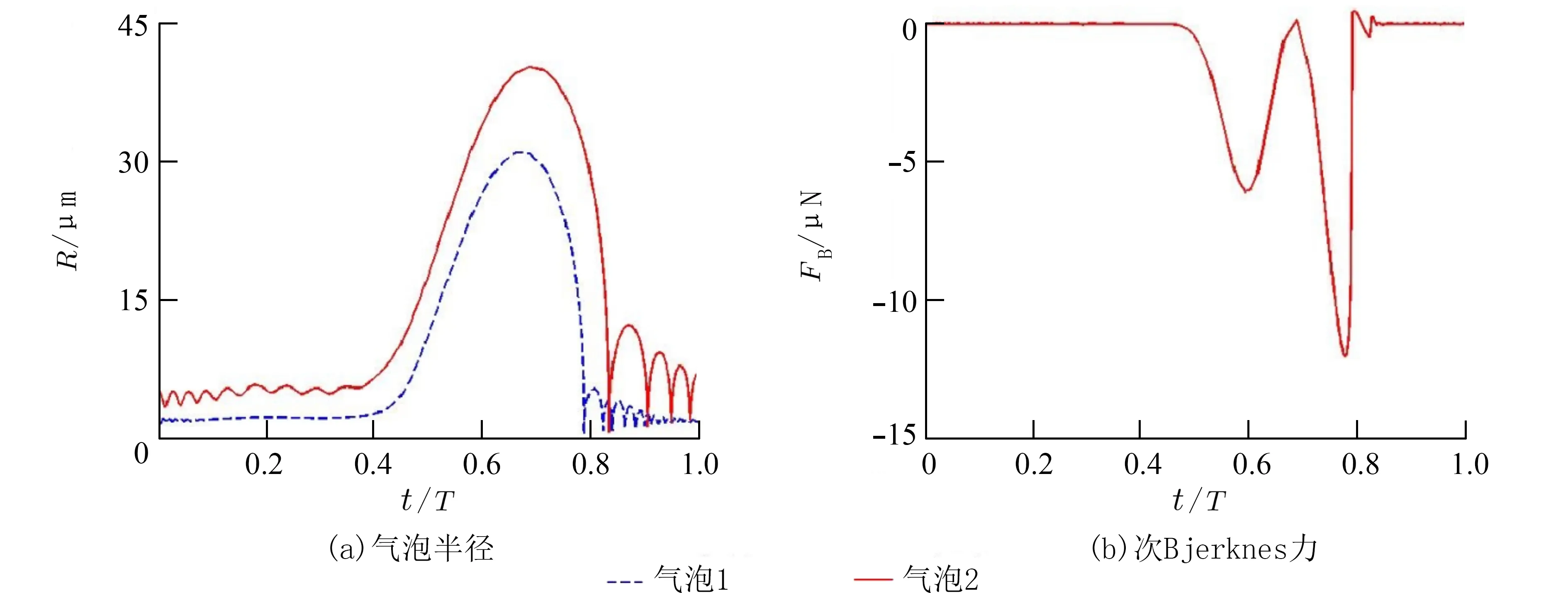
图8 双频驱动f1=40 kHz f2=120 kHzFig.8 Dual frequency drive with frequencies f=40 kHz and f=120 kHz respectively

图9 双频驱动f1=60 kHz f2=180 kHzFig.9 Dual frequency drive with frequencies f=60 kHz and f=180 kHz respectively

3 结论

本文对外部驱动声压pex=p1cos2πf1t+p2cos2πf2t=p1cos2πft+p2cos（3×2πft），初始半径分别为R10=2 μm、R20=5 μm 的耦合双泡的半径演化曲线及气泡间次Bjerknes 力随驱动声压幅值的变化关系进行了计算研究，结果表明：

当声压幅值之比p2∶p1一定时，随着p1的增加，气泡1、2 的最大膨胀半径随之增加、气泡间次Bjerknes 力逐渐增大；当驱动声压幅值p1一定时，随着声压幅值之比p2∶p1的增加，气泡1、2 的最大膨胀半径随之增加，p2∶p1比值越大、耦合双泡的最大膨胀半径越大，气泡间次Bjerknes 力越强.

当驱动声压幅值p1、声压幅值比p2∶p1均一定时，双频驱动频率越高，气泡最大膨胀半径越小，气泡间的次Bjerknes 力随之减小.