带有最优流量信息中断期望影响的一类新格子模型

刘丽梅，化存才

(1.云南民族大学 预科教育学院，云南 昆明 650504；2.云南师范大学 数学学院，云南 昆明 650500)

随着经济的迅速增长以及社会现代化的不断发展，道路上的车辆数量逐年攀升，这也导致交通拥堵和交通事故日益频发.为缓解日趋复杂的交通问题，众多学者对交通流模型进行研究，交通流模型可分为宏观的交通流模型和微观的交通流模型[1-7].1998 年，Nagatani 提出涉及交通流的宏观格子流体动力学模型[8]，这对研究交通流具有里程碑的意义.此后，学者们在此基础上对模型进行了改进，提出了许多考虑不同因素的格子流体力学模型，如李志鹏等[9]在Nagatani's 模型的基础上考虑流量差的影响，并验证考虑流量差的影响能提高交通流的稳定性.田钧方等考虑密度差影响的格子流体力学模型，这对抑制交通拥堵起到积极的作用[10].在现实生活中，驾驶员的个体特征也是影响交通流稳定性的重要因素之一，彭光含等在Nagatani's 模型的基础上考虑驾驶员预估效应的影响[11].Kang 等[12]提出考虑驾驶员反应延迟影响的格子流体力学模型.之后，考虑驾驶员急性、胆量等特征的交通流模型也被学者研究.随着道路交通量的逐渐增多，道路交通环境也时常影响交通流的稳定性.特别的，由行人、事故等因素造成的交通中断是导致交通拥堵的一个重要原因.任何行驶的车辆均有可能出现中断，而交通中断往往是以不确定的概率发生.唐铁桥等[13]，提出考虑前车速度中断影响的车辆跟驰模型.之后，孙棣华等[14]在变道的2 车道格子流体力学模型中加入中断概率，发现变道可以平均各车道的交通量，但当前格子流量中断会使得交通状况恶化.Jiang等[15]考虑后视以及中断共同影响的格子流体力学模型，结果表明2 个因素都能提高交通流的稳定性.彭光含等[16-18]考虑j+2格子最优流量中断的格子流体力学模型.

这些考虑中断影响的模型均能改善交通流的稳定性.在实际交通流中，交通中断概率是驾驶员对可能发生交通中断的预期行为.j+1格子最优流量可看成是驾驶员在行驶过程中根据运行状况预估得到的优化流量，预估中断发生时最优流量变为0，而以往的模型并未考虑j+1格子最优流量中断的期望行为.为此，本文在Nagatani's 格子流体力学模型的基础上，考虑j+1格子最优流量信息中断的期望行为，提出一类新的格子流体力学模型；利用线性稳定和非线性稳定分析方法，得到模型的稳定性条件和对应的mKdV 方程；通过求解mKdV 方程，分析交通密度波传播演变的过程；最后，通过数值仿真验证理论分析的正确性.

1 模型的建立

在1998 年，Nagatani[8]提出最早的格子流体力学模型，其模型方程如下：

式中：ρ0为 平均密度，ρj，vj分别表示在第j格点t时刻的瞬时密度和瞬时速度，a为驾驶员的敏感系数.ρ0V(ρj+1) 表示最优流量，V(ρj+1)为驾驶员根据交通状况预估得到的最优速度，其形式为：

其中：ρc表示安全密度，ρ0表 示平均密度，vmax表示最大行驶速度.

在实际的交通中，交通中断概率是驾驶员对可能发生交通中断的预估行为，为揭示j+1格子最优流量信息中断的期望行为对交通流稳定性的影响，本文在(2)式中添加最优流量中断的概率，提出新的格子流体力学演化方程，模型方程如下：

式中：pj+1表 示优化流量在第j+1格 子中断的概率，为简化计算将中断概率pj+1看成常数p.因此，方程(4)可以写成如下形式：

2 线性稳定分析

对提出的格子流体力学模型(5)进行线性稳定性分析，研究优化流量中断概率的期望行为对交通拥堵演变的影响.在稳定状态下，假设交通流的稳定密度为 ρ0，最优速度为V(ρ0)，得到稳定状态的密度和速度分别为：

假定yj(t)表示格点j上稳定状态密度的小扰动量，此时密度变为：

将(7)式代入(5) 式得

通过展开yj(t)=Aeikj+zt，方程(8)变为：

将z=z1ik+z2(ik)2+···代 入方程(9)，可得到关于 ik的1 阶、2 阶项的系数

当z2>0,交通流是稳定的，但当z2<0时交通流将演化为非稳态流.由此，可得到交通流中性稳定曲线

均匀流的稳定条件可表示为：当p=0时，上述稳定条件变成Nagatani's 模型的稳定条件.

根据(12)式可知，最优流量中断的概率p对交通流的稳定性具有重要的影响.由(11)式可画出扰动中断概率p在取不同值（0，0.1，0.2，0.3）时的中性稳定曲线，如图1 中的实线.图1 中虚线为共存曲线，由后续的非线性分析导出.每条中性稳定曲线都存在一个最高点，被称为临界点 (ρc,ac).在中性稳定线上方的区域交通流是稳定的，而在中性稳定线下方的区域交通流是非稳定的.当p=0，即不存在扰动中断情况时，交通流的中性稳定曲线同Nagatani's 模型，稳定区域的面积最小.之后，随着p的逐渐变大，交通流的临界稳定点和中性稳定线逐渐降低，交通流稳定区域的面积扩大，交通流越稳定.由此说明添加最优流量中断期望影响的格子模型比Nagatani's 模型更稳定.同时增大最优流量扰动中断的概率p能提高交通流的稳定性.

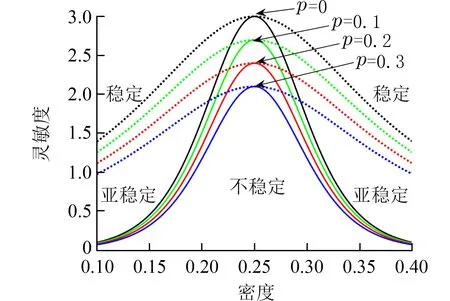
图1 不同扰动中断概率p 下密度与灵敏度的相图Fig.1 The phase diagram of the density and the sensitivity under different interruption probabilities p

3 非线性稳定分析

为研究交通流密度波的传播演变行为，本文将采用还原扰动法在临界点 (ρc,ac)附近导出mKdV 方程分析交通演变的非线性现象.现对空间变量x和时间变量t引入缓慢变量X和T，即

式中：0<ε ≪1，b为待定参数.并且密度为：

将方程(13)～(14)代入到方程(5)中，并对方程(5)进行Taylor 展开至 ε5项，得到如下方程

式中：C表示扭结-反扭结解的传播速度，满足以下可解性条件

M[R0′]=M[R′]，扭结-反扭结解的传播速度C为：

由此，mKdV 方程关于密度的扭结-反扭结孤子解为：

扭结-反扭结孤立波解代表低密度时的自由相和高密度时的拥堵相，共存曲线是由 ρj=ρc±A推导出来的，其中从图1 中可以发现，中性稳定曲线(实线)和共存曲线(虚线)将交通流分成稳定、亚稳定、不稳定3 个区域.随着参数p的逐渐变大，交通流的临界点逐渐变小，共存曲线逐渐降低，交通流不稳定区域的面积逐渐变小，交通流越稳定.即考虑最优流量中断的期望行为对改善交通流的稳定性起着积极的作用.

4 仿真模拟

数值模拟用来验证理论分析的正确性，本节采用周期边界条件，初始条件选取如下[18].

式中：N=100，ρc=ρ0=0.25，a=2.3，vmax=2.

图2 为1 04时间步长之后，扰动中断概率p分别取不同值下的密度波随时间的演变图，图2(a)～(d)分别对应不同的中断概率p=0、0.1、0.2、0.3. 从图2 中可发现当p=0时模型变成Nagatani's 模型，此时，密度波的振幅波动较大交通流极不稳定.但从图2(b)～(d)，随着p逐渐增大，交通流的密度波的振幅逐渐减小，交通流越来越稳定.并且p=0.1、0.2、0.3时的密度波的振幅均低于Nagatani's 模型的振幅，即考虑最优流量信息中断的期望影响的格子模型比Nagatani's 模型更稳定.当p=0.3，满足稳定条件(12)，即使在初始条件下加入小扰动，但随着时间的推移，交通密度波的振幅最终消失，交通流趋于稳定.因此，考虑最优流量中断的概率能提高交通流的稳定性.

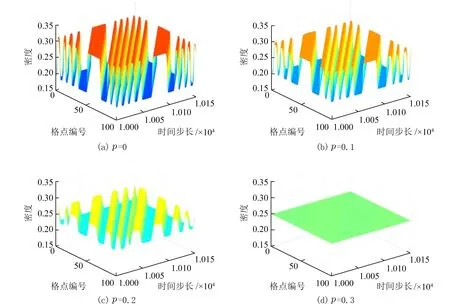
图2 不同扰动中断概率p 下密度波随时间的演化情况Fig.2 The spatiotemporal evolution of density waves for different interruption probability p

为更直观地研究最优流量中断的概率p对交通流密度波的影响，图3 画出了p分别取0、0.1、0.2、0.3不 同参数下：(a)在t=10 300时间步长的瞬时密度分布情况和(b)迟滞回环曲线.图3(a)更能直观地显示，随着最优流量中断的概率p变大，交通流密度波的振幅逐渐变小.同时p=0.1,0.2,0.3曲线的振幅均低于p=0 即Nagatani's 模型的振幅.特别，当p=0.3时，满足稳定条件(12)时，此时交通密度波的振幅保持稳定状态.图3(b)绘制了交通密度与流量关系的迟滞回环图，当迟滞回环区域变小，流量波动的幅度小，交通流稳定.反之，迟滞回环区域大，则流量波动的幅度大，交通流不稳定.当p=0时模型变为Nagatani's 模型，迟滞回环的区域最大，此时交通流极其不稳定.但随着参数p的逐渐增大，迟滞回环的区域变小，交通流量波动的幅度越来越小，交通流越稳定.当p=0.3时，迟滞回环曲线变成一个点，流量保持不变，交通流最稳定.因此，考虑最优流量中断的概率能提高交通流的稳定性.

图3 瞬时密度分布和迟滞回环曲线图Fig.3 The density profile of the density wave and hysteresis loop curve graph

5 结论

交通中断可看成驾驶员对未发生的交通状况的预估行为，为分析最优流量中断的期望行为对交通流稳定性的影响，本文提出了一类扩展的Nagatani's 模型.首先，通过线性稳定分析方法，得到关于最优流量中断概率p影响下的稳定条件，由相图得到，随着p的不断增大，交通稳定区域逐渐增大，并发现含有参数p的格子模型稳定区域比Nagatani's 模型大.其次，采用非线性分析方法，在临界稳定点附近导出mKdV 方程，通过求解方程得到的扭结-反扭结解描述交通密度波的演变过程，并画出共存曲线，进一步验证引入最优流量中断概率p对改善交通拥堵是有效的.最后，利用仿真算例验证了理论分析结果，进一步证明了含有参数p的格子流体力学模型比Nagatani's 模型更能有效地抑制交通拥堵，即考虑最优流量中断的期望行为对提高交通流的稳定性具有积极的影响.

本文探讨添加最优流量中断期望影响的格子模型对交通流稳定性的影响，后续可结合能耗和心理特征等方面，收集与实际相关的多交通信息研究多车道交通流，为仿真和控制提供更多的理论基础.